ما يكمن وراء ثابت Feigenbaum

نعي: ميتشل Feigenbaum ، (1944-2019) ، 4.66920160910299067185320382 ...

ستيفن ولفرام مدونة المادة



ويسمى ثابت Feigenbaum ويساوي حوالي 4،6692016. ويحدث ذلك مع دورية تحسد عليها في أنواع معينة من النظم الرياضية والفيزيائية التي يمكن أن تظهر السلوك الفوضوي.

كان ميتشل فيجنباوم ، الذي تركنا في 30 يونيو في سن 74 ، هو الشخص الذي اكتشفها - في عام 1975 ، وقد فعل ذلك من خلال إجراء الرياضيات التجريبية على آلة حاسبة الجيب.

أصبح هذا الاكتشاف حاسما في نظرية الفوضى . ولكن عندما تم اكتشافها لأول مرة ، كانت هذه النتيجة غير متوقعة وغريبة وغير مرتبطة بأي شيء مما تمت دراسته سابقًا. ومع ذلك ، في بعض النواحي ، حقيقة أن ميتشيل فيجنباوم هو الذي اكتشفني منذ ما يقرب من 40 عامًا اكتشف أنه يبدو مناسبًا.

ميتشل ، الذي درس الفيزياء النظرية ، وكان خبيرًا في تقاليدها الرياضية ، بدا دائمًا أنه يعتبر نفسه غريبًا. كان يشبه بيتهوفن إلى حد ما - وكان له انطباع أنيق بسر فكري معين. غالبًا ما أدلى بتصريحات قوية ، عادةً ما تكون ذات شكل تآمري ، مع وميض في عينيه وكأس من النبيذ أو سيجارة في يده.

وتحدث في جمل طويلة مزخرفة خانت منحة دراسية وفكرية فيه. ولكن الأفكار منه تدفقت أكثر مختلفة. في بعض الأحيان كانت مفصلة والتقنية. كانت هذه في بعض الأحيان قفزات حدسية ، والتي ، على الأقل ، لم أستطع تتبعها. كان دائمًا ما يقرأ شيئًا ، ولم ينام حتى 5-6 ساعات ، وملء الصفحات الصفراء من أجهزة الكمبيوتر المحمولة بالصيغ وتحميل نظام Mathematica بحسابات جبرية معقدة قد تستمر لساعات.

لقد نشر القليل ، وكثيراً ما خيب آماله المنشورة عن حقيقة أن الكثير من الناس لم يفهموها. بحلول وقت وفاته ، كان يعمل لسنوات عديدة في علم البصريات الإدراكية ، وعلى أسئلة مثل "لماذا يبدو القمر أكبر عندما يكون فوق الأفق". ومع ذلك ، لم يقرر نشر أي شيء كهذا.

لأكثر من 30 عامًا ، كان عمل ميتشل الرسمي (الذي حصل عليه ، في الواقع ، بفضل افتتاح ثابت Feigenbaum) أستاذاً بجامعة روكفلر في نيويورك (للقاء بعثة الأبحاث البيولوجية للمعهد ، وتم تعيينه رئيسًا لـ "مختبر الفيزياء الرياضية"). ومع ذلك ، كان لا يزال يقوم بالكثير من العمل ، وقدم اسمه لبدء تشغيل الحوسبة المالية ، وكان مرتبطًا بشكل وثيق باختراع أساليب رسم الخرائط الجديدة لأطلس هاموند العالمي .

ما اكتشف ميتشل

الفكرة الأساسية بسيطة للغاية. خذ الرقم x من 0 إلى 1. سنستبدل بالتدريج x بفأس (1 - x). لنفترض أننا نبدأ بـ x = 1/3 ، و = 3.2. ثم فيما يلي القيم المتسلسلة لـ x التي سنحصل عليها:



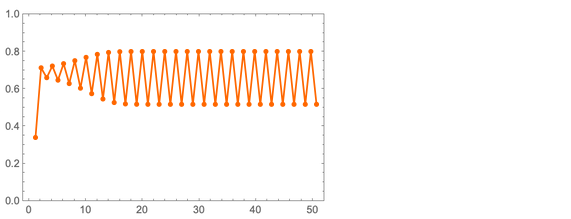
تصبح قيم x دورية ، مع فترة 2. لكن ماذا يحدث إذا أخذنا القيم الأخرى لـ؟ وهنا بعض النتائج لما يسمى ب "الخرائط اللوجستية":



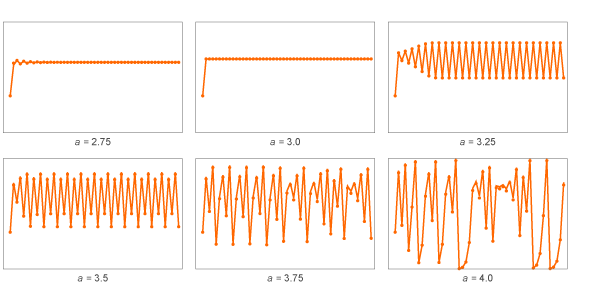
بالنسبة للقيم الصغيرة ، تأتي قيم x بسرعة إلى قيم ثابتة. بالنسبة للحجم الكبير ، تصبح دورية ، أولاً بفترة 2 ، ثم 4. وللأكبر ، تبدأ القيم في القفز بطريقة عشوائية على ما يبدو.

يمكن تلخيص ذلك عن طريق تكوين قيم x (هنا توجد 300 ، بعد إسقاط الخمسين الأولى) كدالة لقيمة:



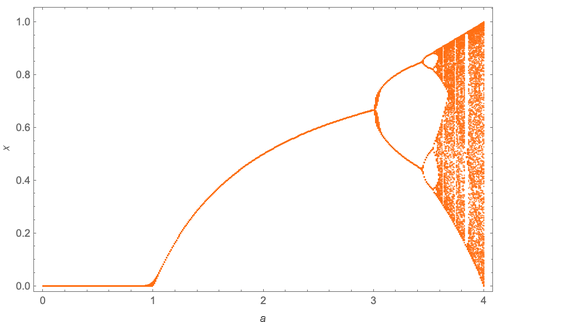
مع زيادة أ ، لوحظ سلسلة من فترة مضاعفة. في هذه الحالة ، تحدث عند 3 = a 3.449، ، ≈ 3.544090 ، ≈ 3.5644072. أشار ميتشل إلى أن هذه القيم المتتالية لها حد (a ≈ ≈ 3.569946) في التسلسل الهندسي ، _∞ - a _n ~ δ ^-n و 69 ≈ 4.669.

نتيجة مثيرة للاهتمام. ولكن هنا ما يعنيه ذلك: هذا صحيح ليس فقط لرسم الخرائط التكرارية x → ax (1 - x)؛ هذا صحيح لأي عرض. هنا ، على سبيل المثال ، هو "مخطط التشعب" لـ x → a sin (π √x):



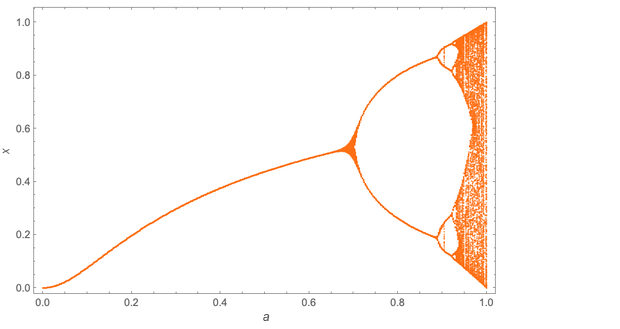
تختلف التفاصيل ، ولكن أشار ميتشل إلى أن ترتيب مضاعفة الفترة يشكل مرة أخرى تسلسلًا هندسيًا بنفس القاعدة تمامًا ≈ 69 4.669.

وليس فقط هذه التعيينات التكرارية المختلفة أعطت نتائج مماثلة نوعيًا ؛ عند قياس معدل التقارب ، اتضح أن يكون هو نفسه تمامًا - دائمًا ≈ ≈ 4.669. كان هذا هو اكتشاف ميتشل الكبير: ميزة عالمية من حيث المقاربة للفوضى في فئة النظم.

الخلفية العلمية

الفكرة الأساسية للتعيينات التكرارية لها تاريخ طويل يعود إلى العصور القديمة. نشأت إصداراتها الأولى فيما يتعلق بالبحث عن تقريبات متعاقبة ، على سبيل المثال ، للجذور التربيعية. على سبيل المثال ، يمكن الحصول على طريقة نيوتن من القرن السابع عشر إلى الثاني بالتكرار x → 1 / x + x / 2. بدءًا من x = 1:



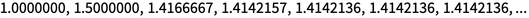
تم إضفاء الطابع الرسمي على فكرة التقريب التكراري لوظيفة تعسفية لأول مرة ، على ما يبدو ، في ورقة عام 1870 من إعداد إرنست شرودر (المعروف بإضفاء الطابع الرسمي على أشياء كثيرة ، من الدرجات إلى الجبر المنطقي) ، على الرغم من أن معظم المناقشات كانت تتعلق بحل المعادلات الوظيفية وليس التكرارات نفسها (باستثناء الدراسة مجالات التقارب بين التقريب النيوتوني الذي قام به آرثر كايلي في عام 1879). في عام 1918 ، أجرى غاستون موريس جوليا دراسة موسعة لوظائف المواد التكرارية على متن الطائرة المعقدة ، واخترع مجموعة جوليا . لكن قبل ظهور فركتلات في أواخر سبعينيات القرن الماضي (والتي سرعان ما أدت إلى ظهور مجموعة ماندلبروت ) ، فإن هذا المجال من الرياضيات زرع.

ولكن بغض النظر عن الأبحاث في الرياضيات البحتة ، بدأت تظهر التعيينات التكرارية بأشكال مشابهة للفأس x (1 - x) في ثلاثينيات القرن العشرين بين النماذج العملية الممكنة لدراسة بيولوجيا السكان أو نظرية دورات الأعمال. ظهرت عادة في شكل إصدارات منفصلة من المعادلات المستمرة ، مثل معادلة Verhulst اللوجستية في منتصف القرن التاسع عشر. كان السلوك المذبذب شائعًا أيضًا - وفي عام 1954 ، وجد ويليام ريكور (أحد مؤسسي الصيد العلمي) سلوكًا أكثر تعقيدًا عند التكرار من خلال منحنيات تكاثر الأسماك التجريبية.

في الرياضيات البحتة ، ظهرت متغيرات التعيينات التكرارية بشكل دوري في نظرية الأعداد. في عام 1799 ، درس كارل فريدريش غاوس ، في الواقع ، رسم الخرائط x → frac (1 / x) فيما يتعلق بالكسور المستمرة. منذ نهاية القرن التاسع عشر ، ظهر الاهتمام في تعيينات الشكل x → frac (ax) وعلاقتها بخصائص a.

مباشرة بعد عمل هنري بوانكاريه بشأن الأساليب الفعالة للميكانيكا السماوية في القرن العشرين ، ظهرت فكرة الحساسية للظروف الأولية ، وفي النهاية لوحظ أن الخرائط التكرارية يمكنها ، في الواقع ، "حفر الأرقام" في الظروف الأولية. على سبيل المثال ، تكرار التكرار x → frac (10 x) فوق الأرقام يغير أساسًا تسلسل الأرقام بموضع واحد إلى اليسار مع كل خطوة:





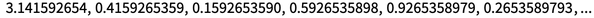
توضح أيضًا تعيينات النوع x → ax (1-x) "حفر الأرقام" مشابهًا (على سبيل المثال ، إذا استبدلت x بـ sin () u) ² ، ثم x → 4 x (1-x) تتحول تمامًا إلى u ← frac (u ، 2) ، وكان هذا معروفًا في الأربعينيات - على سبيل المثال ، علق جون فون نيومان على ذلك في عام 1949 فيما يتعلق بطريقته التكرارية في منتصف المربع لتوليد أرقام عشوائية مزيفة بواسطة جهاز كمبيوتر.

ومع ذلك ، ماذا عن الرياضيات التجريبية القائمة على التعيينات التكرارية؟ لم تكن هناك رياضيات تجريبية على أجهزة الكمبيوتر الرقمية المبكرة (كان وقت الكمبيوتر لمعظمها باهظ التكلفة). ولكن في أعقاب مشروع مانهاتن في لوس ألاموس ، ابتكروا جهاز كمبيوتر MANIAC الخاص بهم ، والذي بدأ في النهاية استخدامه في سلسلة من الدراسات في مجال الرياضيات التجريبية. في عام 1964 ، كتب بول شتاين وستان أولام تقريراً بعنوان "دراسة التحولات غير الخطية على الحواسيب الإلكترونية" ، والذي يعرض صورا لشاشات MANIAC تشبه شاشات الذبذبات والتي تعرض عروض تكرارية لشكل معقد إلى حد ما. في عام 1971 ، أنتج تقرير آخر تم إنشاؤه في لوس ألاموس "بدافع الفضول المطلق" (كتبه نيك متروبوليس ، رئيس مشروع MANIAC ومطور طريقة مونت كارلو ، وكذلك بول شتاين وشقيقه ميرون شتاين) ، نتائج حسابية أكثر تحديدًا للتخطيطات اللوجستية ، ولاحظوا الظاهرة الأساسية المتمثلة في مضاعفة الفترة (أطلق عليها المؤلفون اسم التسلسل U) ، وكذلك المقاومة النوعية للتغيرات في طريقة العرض الأساسية.

بصرف النظر عن كل هذا في الفيزياء والرياضيات ، كانت هناك تطورات أخرى. في عام 1964 ، قدم إد لورينز (عالم الأرصاد الجوية من معهد ماساتشوستس للتكنولوجيا) وأبدع محاكاة لمعادلاته التفاضلية "التي تحدث بشكل طبيعي" باسمه ، حيث تم توضيح الحساسية للظروف الأولية. منذ الأربعينيات من القرن العشرين ، تشكلت مجموعة متواصلة من التطورات الرياضية في نظرية النظم الديناميكية (استند العمل إلى إنجازات Poincare من أوائل القرن العشرين). على وجه الخصوص ، قاموا بالتحقيق في الخصائص العالمية لحلول المعادلات التفاضلية. عادة ، واجه الباحثون نقاطًا ثابتة ، وأحيانًا تحد من الدورات. ومع ذلك ، بحلول سبعينيات القرن العشرين ، خاصة بعد ظهور أول محاكاة للكمبيوتر (كما في لورنتز) ، أصبح من الواضح أن شيئًا آخر يمكن أن يحدث مع المعادلات غير الخطية: ما يسمى بـ " جاذب غريب ." وأثناء دراسة "التعيينات المرتجعة" لجاذبي غريب ، بدأت التعيينات التكرارية تظهر مرة أخرى.

ومع ذلك ، لم يكن حتى عام 1975 أن دراسات مختلفة من التعيينات التكرارية بدأت تتقاطع. في مجال الرياضيات البحتة ، قام صانع النظريات الديناميكية جيم يورك وطالبه تيان ين لي من جامعة ماريلاند بنشر Chaos Follows from Period Three ، حيث أظهروا أن رسم خرائط تكرارية بقيمة معلمة معينة ، الشرط الأولي الذي يؤدي إلى ظهور دورة طولها ثلاثة ، يجب أن تكون هناك شروط أولية أخرى لا تؤدي إلى ظهور دورات - أو ، كما يصفونها ، تظهر الفوضى. ثم تبين أن ألكساندر ساركوفسكي ، ممثل المدرسة السوفيتية لبحوث الأنظمة الديناميكية ، في عام 1962 ، أثبت أنه نتيجة أضعف قليلاً ، حيث تتبع الدورات مع جميع الفترات دورة مع الفترة 3.

في الوقت نفسه ، بدأ الاهتمام بالأخصائيين الموجودين في الرياضيات في بيولوجيا السكان ينمو في التعيينات اللوجيستية ، والتي نشأت منها مراجعة مكتوبة بشكل جيد عام 1976 بعنوان "نماذج رياضية بسيطة مع ديناميات معقدة للغاية" ، تأليف من قبل فيزيائي أسترالي تلقى تعليمه من قبل روبرت ماي ، الذي كان أستاذاً في ذلك الوقت. البيولوجيا في جامعة برينستون (بعد ذلك سوف يصبح المستشار العلمي للحكومة البريطانية وسيحصل على لقب البارون ماي من أكسفورد).

ولكن على الرغم من وجود أشياء مثل الرسومات التخطيطية للتشعب ، فإن اكتشاف خصائصها العددية العالمية كان يجب أن يتوقع ظهور ميتشل فيجنباوم.

ميتشل السفر

نشأ ميتشل فيغنباوم في بروكلين ، نيويورك. كان والده الكيميائي التحليلي ، وكانت والدته تدرس في مدرسة عامة. لم يكن ميتشل يحب الدراسة بشكل خاص ، على الرغم من حصوله على درجات جيدة في امتحانات الرياضيات والعلوم الدقيقة ، وكذلك تعلم تحليل المصارعة بشكل مستقل ولعب البيانو. في عام 1960 ، في سن ال 16 ، دخل ، مثل بعض الأطفال المعجزة ، في كلية مدينة نيويورك ، رسميًا لدراسة الهندسة الكهربائية ، لكنه حضر أيضًا دورات في الفيزياء والرياضيات. بعد تخرجه في عام 1964 ، دخل معهد ماساتشوستس للتكنولوجيا. في البداية أراد الدفاع عن الدكتوراه في الهندسة الكهربائية ، لكنه سرعان ما تحول إلى الفيزياء.

وعلى الرغم من سعادته بالفيزياء الرياضية الكلاسيكية (مثل تلك المقدمة في كتابي لانداو و Lifshitz على سبيل المثال) ، فقد كتب في النهاية رسالة حول الموضوع تم تعيينه من قِبل أمينه - فيزياء الجسيمات وتقييم لفئة مخططات فاينمان لنثر الفوتونات بواسطة جسيمات العددية . لم تكن الرسالة مثيرة للاهتمام ، ولكن في عام 1970 تم إرساله إلى جامعة كورنيل كطالب ما بعد الدكتوراه.

بدأ ميتشل يواجه مشاكل مع التحفيز ، وبدلاً من القيام بالفيزياء ، فضل قضاء بعض الوقت في المقاهي ، وحل الكلمات المتقاطعة في صحيفة نيويورك تايمز (التي تمكن من فعلها بسرعة كبيرة). ولكن في كورنيل ، صنع ميتشل بعض الأصدقاء المهمين. أحدهم كان بريدراج تسفيتانوفيتش ، وهو طالب دراسات عليا بارز من ذلك الجزء من يوغوسلافيا يسمى الآن كرواتيا ؛ درس الديناميكا الكهربائية الكمية ، وشارك مع ميتشل مصلحة في الأدب الألماني. وكان آخرها الشاعرة الشابة كاثلين دوريش (التي أصبحت فيما بعد كاتي هاموند) ، وهي صديقة لبريدراج. وكان آخرها النجم الصاعد للفيزياء ، البروفيسور بيت كاروثرز ، الذي شارك ميتشل اهتمامه بالموسيقى الكلاسيكية.

في أوائل سبعينيات القرن الماضي ، كان العصر الذهبي لنظرية مجال الكم يقترب. لكن على الرغم من موضوع عمله ، لم يفعل ميتشل هذا ، وبعد عامين في كورنيل لم تسفر عن أي نتائج. ومع ذلك ، فقد نجح في إقناع هانز بيث ، ونقله إلى مكان آخر ، وأيضًا في مرحلة ما بعد الدكتوراة ، ولكن إلى معهد يحتل مكانًا أقل قليلاً في التسلسل الهرمي غير الرسمي - كلية فرجينيا للفنون التطبيقية.

في معهد فيرجن ، كان ميتشل أقل من كورنيل. إنه لم يتصل عمليا بالأشخاص ، ولم يقدم سوى عمل واحد على ثلاث صفحات: "علاقة معامل التطبيع ووظيفة التشتت في معادلة النقل للمجموعات المتعددة". كما يوحي الاسم ، كان العمل تقنيًا وغير مهتم.

في نهاية فترة إقامة ميتشل لمدة عامين في فرجينيا ، لم يكن من الواضح ما الذي سيحدث بعد ذلك. ومع ذلك ، تدخل الحظ. تم التعاقد مع صديق ميتشل من كورنيل ، بيت كاروثرز ، لتأسيس وحدة نظرية في لوس ألاموس ، وحصل على جائزة بلانش لتوظيف العديد من علماء الفيزياء الشباب البارزين. أخبرني بيت بفخر (كجزء من نصيحة الإدارة العلمية) أنه كان يشعر أن ميتشل قادر على شيء عظيم ، وعلى الرغم من آراء الآخرين - والأدلة - قرر وضعه عليه.

بعد أن نقل Mitchell إلى Los Alamos ، بدأ Pete في تقديم مشاريع له. في البداية ، كان هذا استمرارًا لعمل بيت ، ومحاولات لحساب مجموعة من الخصائص الجماعية ("النقل") لنظرية مجال الكم من أجل فهم اصطدامات الجسيمات عالية الطاقة - كانت هذه الأعمال التي سبقت الدراسات التي أجريت على بلازما كوارك-غلوون.

ولكن سرعان ما اقترح بيت أن يتعامل ميتشل مع الاضطرابات في السوائل ، على وجه الخصوص ، لمعرفة ما إذا كانت أساليب مجموعة إعادة التعمير ستساعد في هذا الأمر.

عندما يبدأ السائل - على سبيل المثال ، الماء في التدفق بسرعة كافية ، تظهر دوامات صغيرة فيه ، ويبدأ في التصرف بطريقة معقدة ، للوهلة الأولى ، بطريقة عشوائية. ولكن على الرغم من أن هذه الظاهرة قد نوقشت نوعيًا لعدة قرون (على سبيل المثال ، حتى ليوناردو دافنشي صنع رسوماته) ، فقد استطاع الفيزيائيون أن يرووا عنها بشكل ملحوظ - على الرغم من أن أندريه نيكولاييفيتش كولموغوروف في الأربعينيات من القرن الماضي أدلى بتصريح مفاده أن دوامات المياه يجب أن تشكل سلسلة - توزيع الطاقة. في لوس ألاموس ، ركز العلماء على تطوير أسلحة ذرية (والتي تنطوي حتماً على دراسة سلوك السوائل ذات التيارات القوية) ، وكان الاضطراب مهمًا للغاية لفهمه - على الرغم من أنه لم يكن من الواضح كيفية التعامل معه.

في عام 1974 ، ظهر خبر أن كينيث ويلسون من كورنيل "حل مشكلة كوندو" [مشكلة كوندو هي عجز الفيزياء النظرية عن تفسير تأثير / كوندو تقريبًا. عبر.] باستخدام تقنية تسمى "مجموعة إعادة التهيئة". اقترح بيت كاروثرز أن يقوم ميتشل بتطبيق هذه التقنية على الاضطرابات.

ترتبط مجموعة إعادة التهيئة بكيفية تأثير تغيير المقياس (أو المعلمات الأخرى) على وصف (وسلوك) الأنظمة. لقد حدث أن دكتوراه ميتشل من معهد ماساتشوستس للتكنولوجيا ، فرانسيس لوي ، مع موراي جل مان ، أعاد تقديمها في عام 1954 في سياق الديناميكا الكهربائية الكمية. كانت الفكرة بلا حراك لعدة سنوات ، لكنها عادت في السبعينيات من القرن الماضي وطبقت بنشاط - وإن كان بطرق مختلفة - على كل من فيزياء الجسيمات (وخاصة ديناميكا الألوان الكمومية ) وفيزياء المادة المكثفة.

في قطعة من الحديد في الغرفة ، يمكنك محاذاة تدور جميع الإلكترونات المرتبطة بكل ذرة ، وبعد ذلك سيتم ممغنطة الحديد. ولكن إذا قمت بتسخين المكواة ، تبدأ التقلبات فيه وفجأة - عند درجة حرارة أعلى مما يسمى. نقاط كوري (770 درجة مئوية للحديد) - تظهر الكثير من العشوائية في الحديد بحيث تختفي خصائصها المغناطيسية. بشكل عام ، هناك عدد غير قليل من المواقف (الذوبان ، الغليان ، تشكيل الازدحام المروري) عند هذا ما يسمى المفاجئ المرحلة الانتقالية .

ولكن ماذا يحدث بالضبط خلال المرحلة الانتقالية؟ أعتقد أن أسهل طريقة لرؤية ذلك هي عن طريق دراسة نظيره في مجال الأوتوماتة الخلوية. مع وجود قاعدة معينة ، مذكورة أدناه ، عندما لا يحتوي النظام في البداية على عدد كبير من الخلايا السوداء ، سيتحول لونه إلى اللون الأبيض قريبًا. ولكن إذا قمت بزيادة عدد الخلايا السوداء الأصلية (عن طريق القياس مع زيادة في درجة حرارة النظام المغناطيسي) ، فجأة ، في هذه الحالة ، مع نسبة 50 ٪ من الخلايا السوداء ، يحدث تحول حاد ، والنظام بأكمله يتحول إلى اللون الأسود (ملاحظة للخبراء حول التحولات الطورية: نعم ، هذا هو انتقال المرحلة في نظام أحادي البعد ؛ يمكن أن تكون هناك حاجة إلى ثنائي الأبعاد فقط إذا كان النظام يحتاج إلى عكس مجهرياً ).



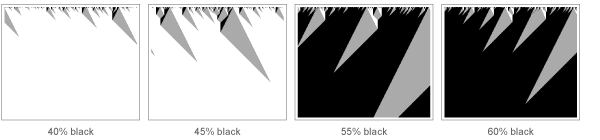
ولكن ماذا يحدث للنظام بالقرب من حدود خلايا سوداء بنسبة 50 ٪؟ في الواقع ، لا يمكنها أن تقرر ما إذا كانت ستصبح سوداء أم بيضاء. نتيجة لذلك ، فإنه يظهر تسلسل هرمي كامل من التقلبات ، من الأصغر إلى الأكبر. وبحلول الستينيات ، أصبح من الواضح أن "الدعاة الحرجين" الذين يميزون قوانين القوة التي تصف هذه التقلبات متماثلون في العديد من الأنظمة.

ولكن كيف نحسب هذه الأسس الحاسمة؟ في بعض الحالات المصطنعة ، كانت الأساليب التحليلية معروفة. ولكن بالنسبة للجزء الأكبر ، كان هناك شيء آخر مطلوب.في أواخر الستينيات ، أدرك كين ويلسون أنه يمكن استخدام مجموعات إعادة التعمير وأجهزة الكمبيوتر. من الممكن بناء نموذج لتفاعل الدورات الفردية. لكن مجموعة إعادة التهدئة تمنحك إجراء "تحجيم" لتفاعلات المزيد والمزيد من كتل الدوران. ومن خلال دراسة ذلك على جهاز كمبيوتر ، تمكن كين ويلسون من البدء في حساب الأسس المهمة.

في البداية ، لم يولي الفيزيائيون الاهتمام اللازم لهذا ، لأسباب ليس أقلها أنهم لم يعتادوا على هذا الاستخدام النشط لأجهزة الكمبيوتر في الفيزياء النظرية. ولكن بعد ذلك ظهرت مشكلة كوندو. في معظم المواد ، تنخفض المقاومة الكهربائية مع انخفاض درجة الحرارة (وفي الموصلات الفائقة تقل إلى صفر حتى في درجات حرارة أكبر من الصفر المطلق). ومع ذلك ، أظهرت قياسات الذهب في الثلاثينات من القرن الماضي أن مقاومته تزداد في درجات حرارة منخفضة. بحلول الستينيات من القرن الماضي ، كان يُعتقد أن الأمر برمته هو تشتت الإلكترونات بواسطة الشوائب المغناطيسية - ومع ذلك ، فقد واجهت الحسابات مشكلة ، مما أسفر عن النتائج اللانهائية في النتائج.

ثم في عام 1975 ، طبق كين ويلسون أساليبه في مجموعة إعادة التعمير - وكان قادرًا على حساب التأثير بدقة. لا يزال هذا التأثير يكتنفه بعض الغموض (ربما يرجع ذلك إلى حقيقة أنني كنت غالباً ما أجد صعوبة في فهم تفسيرات كين ويلسون حول هذا الموضوع ، على الأقل منذ أن قابلته في الثمانينيات). لكن الفكرة القائلة إن مجموعة إعادة التعمير قد تكون مهمة قد ترسخت.

كيف يمكن تطبيقها على الاضطرابات السوائل؟ أعطى قانون السلطة Kolmogorov أفكار معينة. ولكن هل كان من الممكن أخذ معادلات Navier-Stokes التي تتحكم في تدفق السائل المثالي واستخلاص أي منها؟ اتخذ هذا المشروع من قبل ميتشل Feigenbaum.

اكتشاف كبير

من الصعب للغاية التعامل مع معادلات Navier-Stokes. حتى يومنا هذا ، ليس من الواضح للغاية كيف تنشأ حتى أكثر خصائص الاضطراب وضوحا ، أي العشوائية الواضحة. ربما هذه المعادلات ليست وصفًا رياضيًا كاملاً أو ثابتًا ، ونرى في الواقع حركات مجهرية معززة للجزيئات. ربما - كما هو الحال في نظرية الفوضى ومعادلات لورنتز - كل شيء هو تعزيز العشوائية في الظروف الأولية. أنا شخصياً ، استنادًا إلى عملي منذ الثمانينيات ، أعتقد أن بيت القصيد يكمن في خصائص حساباتهم الداخلية ، على غرار العشوائية في " القاعدة 30 " الخاصة بي لأتمتة الخلوية.

كيف تعامل ميتشل مع هذه المشكلة؟ حاول تبسيطها - أولاً من خلال الانتقال من المعادلات التي تعتمد على المكان والزمان إلى المعادلات التي تعتمد فقط على الوقت ، ثم جعلها منفصلة ودراسة تعيينات التكرار. من بول شتاين ، كان ميتشل على دراية بالعمل السابق في عمليات التعيين التكراري التي تمت في لوس ألاموس (والتي لم تكن معروفة على نطاق واسع). لكن ميتشل لم يفهم أي طريقة للمضي قدمًا ، على الرغم من أنه تلقى تحت تصرفه آلة حاسبة جديدة تمامًا قابلة للبرمجة HP-65 ، فقد قرر برمجة العروض التكرارية عليها

ثم ، في يوليو 1975 ، ذهب ميتشل إلى اجتماع بدني صيفي في آسبن ، كولورادو. هناك التقى مع ستيفن سمايل ، عالم الرياضيات الشهير الذي درس النظم الديناميكية ، وفوجئ عندما علم أنه يتحدث عن تعيينات تكرارية. ذكر سمال أن شخصا ما يطلب من الممكن للتعبير عن فترة الحد مضاعفة شلال مع _∞ ≈ 3.56995 عبر الثوابت π نوع القياسية و√2. لم تعرف Smale إجابة هذا السؤال. ومع ذلك ، أصبح ميتشل مهتمًا بهذا ، وقرر محاولة معرفة الإجابة.

لم يكن لديه HP-65 معه ، لكنه اندمج في هذه المسألة باستخدام أدوات قياسية لفيزيائي رياضي متعلم ، وسرعان ما حول المهمة إلى بحث عن أعمدة وظيفية على متن الطائرة المعقدة ، وهو ما لم يكن لديه ما يقوله. ومع ذلك ، عاد إلى Los Alamos في أغسطس ، ثم التفت إلى HP-65 ، وبدأ في برمجتها من أجل اكتشاف نقاط التشعب a _n .

بالنسبة لـ n الصغيرة ، تمت عملية التكرار بسرعة كبيرة. بالنسبة لـ n = 5 ، استغرق الأمر 30 ثانية. ل n = 6 ، كان علي الانتظار عدة دقائق بالفعل. ومع ذلك ، بينما كانت الآلة الحاسبة تعمل ، قرر ميتشل أن ينظر إلى قيم _n التي كان يمتلكها بالفعل ، ولاحظ شيئًا ما: يبدو أنهم يحاولون هندسيًا تحقيق بعض القيمة النهائية.

في البداية ، استخدم ببساطة هذه الحقيقة لتقدير _∞ ، على الرغم من كل المحاولات ، لم يستطع التعبير عنها من خلال الثوابت القياسية. لكنه سرعان ما بدأ يشك في أن الأس التقارب δ كان أكثر أهمية من _∞ - حيث بقيت قيمته دون تغيير مع التغييرات البسيطة في المتغيرات في الخريطة. لمدة شهر تقريبًا ، حاول ميتشل التعبير عن δ من حيث الثوابت القياسية.

لكن بعد ذلك ، في أكتوبر 1975 ، أشار إلى أن بول شتاين قال إن مضاعفة فترة ما تبدو متشابهة ليس فقط من أجل تعيينات لوجستية ، ولكن بشكل عام لجميع التعيينات التكرارية بحد أقصى واحد. بعد أن جمع شمله مع HP-65 بعد رحلة إلى Caltech ، جرب Mitchell على الفور الشاشة x → sin (x) ووجد أنه مع وجود ثلاثة منازل عشرية ، كان الأس ـ تمامًا.

قرر على الفور أنه عثر على شيء رائع. لكن شتاين قال إنه سيحتاج إلى المزيد من الأرقام لاستخلاص النتائج. كان هناك الكثير من أجهزة الكمبيوتر القوية في لوس ألاموس ، لذلك في اليوم التالي ، طلب ميتشل من شخص ما أن يريه كيفية كتابة برنامج فورتران للمضي قدمًا - وبحلول نهاية اليوم كان قادرًا على حساب أنه في كلتا الحالتين - كانت قيمة حوالي 4.6692 .

كان الكمبيوتر الذي استخدمه هو العمود الفقري النموذجي لعلوم الولايات المتحدة في تلك الأيام: طراز CDC 6000 (نفس النوع الذي استخدمته عندما انتقلت إلى الولايات المتحدة لأول مرة في عام 1978). تم تطويره بواسطة Seymour Cray ، واستخدمت افتراضيًا أرقام الفاصلة العائمة 60 بت. ولكن مع هذه الدقة (14 رقمًا بعد العلامة العشرية) ، لم يتمكن ميتشل من الحصول على أي شيء أفضل من 4.6692. لحسن الحظ ، كانت زوجة بيت ، لوسي كاروثرز ، مبرمجة في لوس ألاموس ، وأوضحت ميتشل كيفية استخدام الدقة المزدوجة. كنتيجة لذلك ، كان قادرًا على حساب ما يصل إلى 11 منزلة عشرية ، وتحديد أن قيمتين معينتين تكراريتين مختلفتين متماثلتان.

على مدار عدة أسابيع ، اكتشف ميتشل أن δ يبدو أنه قيمة عالمية لجميع خرائط التكرار بحد أقصى تربيعي واحد. لكنه لم يكن يعرف سبب حدوث ذلك ، ولم يكن لديه أي جهاز رياضي محدد لدراسة هذه المسألة. لكن في النهاية ، في عمر الثلاثين ، اكتشف ميتشل شيئًا يبدو مثيرًا للاهتمام بالنسبة له.

في عيد ميلاده في 19 ديسمبر ، التقى ميتشل مع صديقه بريدراج وأخبره عن هذه النتيجة. ومع ذلك ، في ذلك الوقت ، كان بريدراج يعمل مع فيزياء الجسيمات السائدة ، ولم يعلق أهمية كبيرة على ذلك.

واصل ميتشل العمل ، وبعد بضعة أشهر أصبح مقتنعًا بأن الأس ليس فقط - بل كان عالميًا - بالمقاييس المناسبة ، كانت التعيينات التكرارية ذاتها عالمية. في أبريل 1976 ، كتب ميتشل تقريرا عن النتائج التي توصل إليها. في 2 مايو 1976 ، تحدث عنهم في محاضرة في معهد البحوث المتقدمة في برينستون. كان برادراج هناك ، ثم أصبح أخيرًا مهتمًا بعمل ميتشل.

لكن في كثير من الأحيان لم يكن بريدراج واضحًا بشأن ما يتحدث عنه ميتشل. ولكن في اليوم التالي ، نجح Predrag في تبسيط المهمة والحصول على معادلة وظيفية واحدة فورية للنموذج المحدود لخريطة التكرار المقيس: g (g (x)) = -g (α x) / α ، حيث α ≈ 2.50290 ، مما يعني ضمناً أنه بالنسبة لأي تعيين تكراري من نوع معين ، سيبدو شكله المحدود وكأنه إصدار أكثر تعقيدًا من هذا التعيين:

كيف تطور كل شيء

اكتسب مجال البحث عن التعيينات التكرارية زخماً في 10 يونيو 1976 بعد نشر مراجعة في مجلة Nature by Robert May ، والتي كتبها بشكل مستقل عن ميتشل ، وبطبيعة الحال ، دون ذكر النتائج التي حصل عليها. ولكن في الأشهر التي تلت ذلك ، سافر ميتشل مع تقاريره عن نتائجه. كان رد فعلهم مختلطًا. اهتم الفيزيائيون بكيفية ارتباط هذه النتائج بالفيزياء. لم يفهم علماء الرياضيات وضعهم ، بالنظر إلى أنهم حصلوا عليها من الرياضيات التجريبية ولم يكن لديهم دليل رياضي رسمي. وكالعادة ، كان من الصعب على الناس فهم تفسيرات ميتشل.

في خريف عام 1976 ، حصل بريدراج على شهادة جامعية في جامعة أكسفورد ، وفي اليوم الأول وصلت إلى هناك ، طالبًا يبلغ من العمر 17 عامًا يكتب دبلومًا في فيزياء الجسيمات ، التقيت به. تحدثنا أساسًا عن أسلوبه الأنيق "بصمة الطيور" في العمل مع نظرية المجموعة (كتاب نشر أخيرًا بعد 32 عامًا). حاول أيضًا شرح الخرائط التكرارية لي. وما زلت أتذكر كيف تحدث عن نموذج مثالي لسكان الأسماك في البحر الأدرياتيكي (فقط بعد سنوات قمت بربط هذا مع حقيقة أن بريدراج كان من تلك الأماكن التي تسمى الآن كرواتيا).

في ذلك الوقت لم أعلق أي أهمية على ذلك ، لكن فكرة التعيينات التكرارية أصبحت راسخة في ذهني ، وسرعان ما اختلطت مع فكرة النمطي هندسي متكرر ، والتي تعلمتها من كتاب Benoit Mandelbrot . وعندما ركزت ، بعد بضع سنوات ، على مشاكل التعقيد ، ساعدتني هذه الأفكار في الوصول إلى أنظمة مثل automata الخلوية.

ولكن في عام 1976 ، سافر ميتشل (حتى لقائي القادم مع عدة سنوات أخرى) بنشاط مع تقارير عن النتائج. كما قدم العمل إلى المجلة العلمية المرموقة Advances in Mathematics. لمدة ستة أشهر لم يتلق أخبارًا من هناك ، لكن في النهاية تم رفض العمل. حاول مرة أخرى ، وإرسال وظيفة أخرى إلى مجلة SIAM للرياضيات التطبيقية - مع نفس النتيجة.

أريد أن أقول إنني لست متفاجئًا بهذا. في تجربتي للمنشورات في الأدب الأكاديمي (الذي لم أقم به منذ فترة طويلة) ، فإن نشر عمل في مجال محدد من البحوث أمر سهل للغاية. لكن العمل في مجال شيء جديد أو أصلي حقًا يمكن أن يعتمد عملياً على رفضه بعد تقييم خبير - إما بسبب قصر النظر الفكري أو بسبب الفساد الأكاديمي. واجه ميتشل مشكلة أخرى - كان من الصعب فهم تفسيراته.

لكن أخيرًا ، في عام 1977 ، وافق جويل ليبوفيتز ، محرر مجلة الفيزياء الإحصائية ، على نشر أعمال ميتشل - في الواقع ، لأنه قابله ، لأنه اعترف بأنه لم يفهم العمل. لذلك ظهر عام 1978 "العالمية الكمية في فئة التحولات غير الخطية" ، واصفا الإنجاز العظيم الذي حققه ميتشل. من أجل تحديد الأولويات الأكاديمية ، استشهد ميتشل في بعض الأحيان بموجز للتقرير الذي أعده في 26 أغسطس 1976 ، ونشر في المجموعة السنوية لتقارير لوس ألاموس للنظرية 1975-1976. تأثر ميتشل إلى حد كبير بالرفض لنشر أعماله ، وظل لسنوات يحتفظ برسائل مرفوضة في أحد الأدراج.

واصل ميتشل السفر في جميع أنحاء العالم مع تقارير عن النتائج. كان هناك اهتمام بهم ، ولكن كان هناك حيرة. ومع ذلك ، حدث شيء مدهش في صيف عام 1979: أبلغ ألبرت ليبهابر من باريس عن نتائج تجربة فيزيائية حول الانتقال إلى الاضطرابات في التدفقات الحاملة للهيليوم السائل ، حيث رأى مضاعفة الفترة بالضبط مع الأس - والتي حسبها ميتشل. لقد اتضح أنه ليس عالميًا بالنسبة لفئة النظم الرياضية فحسب ، بل أثبت أيضًا أنه في النظم الفيزيائية الحقيقية.

وعلى الفور أصبح ميتشل مشهورًا. تم اكتشاف علاقة مع مجموعة إعادة التوحيد ، وأصبح عمله عصريًا لكل من الفيزيائيين والرياضيين. استمر ميتشل في ركوب التقارير ، لكن الآن أتيحت له الفرصة للتسكع بانتظام مع أفضل علماء الفيزياء والرياضيات.

أتذكر كيف جاء إلى Caltech ، في وقت ما في خريف عام 1979. كل هذا يشبه لقاء مع نجم الروك. وصل ميتشل ، وقدم تقريرًا أنيقًا ولكنه غامض بعض الشيء ، ثم سرقه ريتشارد فاينمان وموراي جيل مان لإجراء محادثة خاصة.

سرعان ما عُرض على ميتشل مجموعة من الوظائف الرفيعة المستوى المختلفة ، وفي عام 1982 عاد مع النصر إلى Caltech كأستاذ في الفيزياء. كان هناك حديث بأن الاكتشاف يستحق جائزة نوبل ، وبحلول يونيو عام 1984 ظهر في مجلة نيويورك تايمز ، مع بيتهوفن الأنيق ، وسط شلال كورنيل:



لكن علماء الرياضيات ظلوا غير راضين. كما في حالة بينوا ماندلبروت ، فقد اعتبروا أن نتائج ميتشل هي "فرضيات عددية" ، غير مثبتة ، ولا تستحق الذكر. ومع ذلك ، سرعان ما بدأ أفضل علماء الرياضيات (الذين أقام معهم ميتشل صداقات) في حل هذه المشكلة ، ولم تكن النتائج طويلة في المستقبل - على الرغم من أن الأمر استغرق عشر سنوات لاستكمال وإثبات نهائي لعالمية δ.

أين ذهب العلم

ماذا حدث لاكتشاف ميتشل الرئيسي؟ ، بالطبع ، أصبحت مشهورة. وسرعان ما تم العثور على شلالات ذات فترة مضاعفة مع خصائصها العالمية في عدد من الأنظمة - في السوائل والبصريات ، إلخ. ولكن كيف كانت شائعة؟ هل يمكن توسيعها لتغطية كامل مشكلة الاضطراب في السائل؟

درس ميتشيل وآخرون أنظمة أخرى غير التعيينات التكرارية والظواهر ذات الصلة. ولكن من بينها لم تكن مفاجئة مثل اكتشاف ميتشل الأول.

بمعنى ما ، كانت محاولاتي لدراسة الأتمتة الخلوية وسلوك البرامج البسيطة ، التي بدأت في عام 1981 ، تهدف إلى البحث عن بعض الأسئلة الكبيرة التي قد يؤدي إليها عمل ميتشل. ومع ذلك ، كانت أساليبنا ونتائجنا مختلفة للغاية. حاول ميتشل دائمًا أن يبقى على مقربة من أشياء يمكن أن يلجأ إليها الفيزيائيون الرياضيون ، وذهبت دون خوف إلى عالم الحوسبة ، واستكشف الظواهر التي واجهتها هناك.

حاولت أن أفهم كيف يمكن أن يرتبط عمل ميتشل بأعمالي ، وفي أول عمل لي بشأن الأتمتة الخلوية في عام 1981 ، لاحظت ، على سبيل المثال ، أن متوسط ​​كثافة الخلايا السوداء في الخطوات المتعاقبة في تطور الأوتوماتيكية الخلوية يمكن تقديره تقريبًا من خلال رسم الخرائط التكرارية.

أشرت أيضًا إلى أن التطور الكامل لأتمتة الخلوية الرياضية يمكن اعتباره خريطة تكرارية - وإن لم يكن على مجموعة من الأرقام الحقيقية العادية ، ولكن على مجموعة كانتور . في عملي الأول ، قمت ببناء تناظري لتعيينات ميتشل السلسة ، ومع ذلك ، فقد كانت وحشية ومتقطعة في لي:



لكن ، بغض النظر عن الطريقة التي حاولت بها ، لم أجد أي روابط واضحة بعمل ميتشل. كنت أبحث عن نظائرها لمضاعفة الفترة أو ترتيب Sharkovsky ، لكنني لم أجد أي شيء مميز. بالنسبة لمنصة الحوسبة الخاصة بي ، فإن التفكير في الأعداد الحقيقية بتسلسلها اللانهائي من الأرقام أمر غير طبيعي. بعد عدة سنوات ، في كتاب "نوع جديد من العلوم" ، أدخلت ملاحظة "رسم الخرائط التكرارية السلس". لقد أظهرت تسلسل الأعداد ولاحظت كيف أن اكتشاف ميتشل يعني وجود بنية متداخلة غير عادية في بداية التسلسل:

نهاية القصة

ماذا حدث لميتشل؟ بعد أن أمضى أربع سنوات في كورنيل ، انتقل إلى جامعة روكفلر في نيويورك ، وقاد وجودًا بوهيميًا تقريبًا لمدة 30 عامًا ، وقضى معظم وقته في شقته في أبر إيست سايد في مانهاتن.

أثناء تواجده في لوس ألاموس ، تزوج ميتشل من امرأة من أصل ألماني يدعى كورنيليا ، شقيقة الفيزيائي (وصديقي منذ فترة طويلة) ديفيد كامبل ، الذي أسس مركز الدراسات غير الخطية في لوس ألاموس ، ثم أصبح رئيس جامعة بوسطن. ومع ذلك ، بسرعة ، غادر كورنيليا ميتشل ، ولا شيء غير بيت كاروثرز. في وقت لاحق ، جمع بيت ، الذي يعاني من إدمان الكحول وغيرها من المشاكل ، شمل زوجته لوسي ، لكنه توفي في عام 1997 عن عمر يناهز 61 عامًا.

في كورنيل ، التقى ميتشل مع جونيلا ، التي هربت في سن الرابعة عشرة من عائلة القس من بلدة صغيرة في شمال السويد ، وكانت في البداية عارضة أزياء مع سلفادور دالي ، ثم جاءت إلى نيويورك كعارضة أزياء في عام 1966. كان جونيلا صحفياً ، مسجلاً بالفيديو ، وكتب مسرحيات ورسم صورًا. تزوجا من ميتشل في عام 1986 ، واستمر زواجهما لمدة 26 عامًا ، حيث عمل جونيلا في مهنة جيدة في الفن التصويري .

تم نشر أحدث عمل ، كتبه ميتشل من تلقاء نفسه ، في عام 1987. كما نشر العديد من الأعمال مع مؤلفين مختلفين ، على الرغم من أنه لم يتم التنويه بأي منها. واصل معظمهم بحثه المبكر ، أو حاول تطبيق الأساليب التقليدية للفيزياء الرياضية على مختلف الظواهر المعقدة المشابهة لتدفق السوائل.

أحب ميتشل التفاعل مع المراتب العليا في الأوساط الأكاديمية. حصل على جميع أنواع الجوائز والتقدير (باستثناء جائزة نوبل). لكن حتى النهاية اعتبر نفسه غرباء - رجل عصر النهضة ركز على الفيزياء ، لكنه لم يؤمن إيمانا تاما بجميع المؤسسات والممارسات.

منذ أوائل الثمانينات ، رأيت بانتظام مع ميتشل في نيويورك وأماكن أخرى. لقد استخدم منصة Mathematica يوميًا ، وأشاد بها ، وكثيراً ما تحدث عن الحسابات المعقدة التي قام بها معها. مثل العديد من علماء الفيزياء الرياضية ، كان ميتشل خبيرًا في الوظائف الخاصة ، وكثيراً ما تحدث معي حول وظائف أكثر وأكثر غرابة ، والتي ، في رأيه ، يجب أن نضيفها إلى المنتج.

وكان ميتشل اثنين من الهوايات الرئيسية خارج المجال الأكاديمي. في منتصف الثمانينيات من القرن الماضي ، كانت الشاعرة الشابة ، التي تُدعى الآن كاتي هاموند ، والتي عرفها ميتشل من كورنيل ، مديرة إعلانات لصحيفة نيويورك تايمز ، وتزوجت من رجل من عائلة تملكها دار هاموند للأطلس العالمية للنشر. من خلاله ، سقط ميتشل في عالم جديد تمامًا من رسم الخرائط.

لقد تحدثت معه حول هذا الموضوع عدة مرات. لقد كان فخوراً بكشفه عن كيفية استخدام نظرية Riemann لرسم الخرائط للحصول على تعيينات محلية خاصة عند إنشاء الخرائط. وصف لي خوارزمية قائمة على الفيزياء لوضع الملصقات على الخرائط (على الرغم من أنني ما زلت لا أفهمه تمامًا). كان مسروراً للغاية بإصدار الإصدار الجديد من أطلس هاموند (الذي أطلق عليه فيما بعد "أطلس").

منذ الثمانينيات من القرن العشرين ، تطور اتجاه تطبيق الأفكار المادية على التمويل الكمي بنشاط ، وغالباً ما يصبح الفيزيائيون محللين في وول ستريت. وبما أن الممولين يبحثون باستمرار عن مزايا فريدة ، فهناك دائمًا اهتمام بطرق جديدة. غالبًا ما تم الاتصال بي بأسئلة مشابهة - لكن بعد نجاح كتاب James Gleick عام 1987 "Chaos" (الذي أجرى مقابلة مطولة حوله) ، ظهر حشد كبير من الناس أرادوا معرفة كيف يمكن أن تساعدهم "الفوضى" في إدارة شؤونهم المالية.

كان واحد منهم شخص مايكل جودكين . درس في الكلية في أوائل 1960s ، أسس شركة أبحاث القانون لطلاب القانون. بعد ذلك بسنوات قليلة ، قام بتعيين العديد من الاقتصاديين الذين فازوا بجائزة نوبل ، وأنشأ ، ربما ، أول صندوق تحوطي يتعامل مع تجارة المراجحة باستخدام أجهزة الكمبيوتر. كان جودكين موتو طوال حياته ، وكان يحب لعب القمار والسفر والجدول ، وكسب الكثير من المال. في إحدى اللحظات المؤسفة ، كان يبحث عن حل جديد - واكتشف نظرية الفوضى وميتشل فيغنباوم.

عمل في العديد من الفيزيائيين لعدة سنوات ، ثم في عام 1995 قام بتجميع فريق وأسس شركة Numerix لتسويق استخدام أساليب الحساب الفيزيائية في مجال الأدوات المالية الغريبة بشكل متزايد. كان ميتشل Feigenbaum وجه الشركة ، على الرغم من صديقي القديم نايجل غولدفيلد وزميله الشاب ساشا سوكول قاموا بكل هذا العمل الشاق.

منذ البداية ، كان للشركة الكثير من الأعمال المتعلقة بالفيزياء الرياضية ، وشارك ميتشل بنشاط في ذلك. لقد كان من كبار محبي حساب التفاضل والتكامل العشوائي لإيتو ، وحاضر في ذلك ، وكان فخوراً بإيجاد طريقة للتعجيل بالتكامل العشوائي بألف مرة. ومع ذلك ، قامت الشركة بالفعل بكتابة مكتبات في C ++ لدمجها في النظم المصرفية. لم يرغب ميتشل في فعل شيء كهذا على المدى الطويل. بعد عدة سنوات من العمل ، انخفض نشاطه في الشركة.

قابلت جودكين في عام 1998 ، ثم بعد 14 عامًا. وقبل ذلك بفترة وجيزة ، كتب سيرة ذاتية بعنوان "الإجابة الخاطئة للحصول على أسرع: تاريخ سري لإنشاء آلة تداول تريليون" ، وتواصلت معي فجأة ، ودعاني للمشاركة في عمل جديد غامض. ما زال ميتشل يتحدث جيدًا عن مايكل ، على الرغم من أن المحادثة عندما ذهبت فجأة أسست شركة جديدة وأصبحت مديرها ، إلا أنني رفضت.

طوال كل هذه السنوات ، تحدثت غالبًا مع Mitchell ، على الرغم من أن اتصالاتنا لم يتم حفظها جيدًا في الأرشيف بقدر الإمكان ، لأنه كان يحب التحدث بصوتًا أكثر من البريد. لقد كتب لي مرة واحدة: "أنا لا أحب المراسلة عبر البريد الإلكتروني. ما زلت تفضل سماع الصوت والتفاعل مع الشخص ".

لكن تم حفظ بعض الأجزاء في أرشيفي. هناك ، على سبيل المثال ، مراسلات بخصوص عيد ميلاد ميتشل الستين في عام 2004 ، وهو الأمر الذي لم أحصل عليه ، لأنه يتقاطع مع عيد ميلاد أحد أطفالي. بدلاً من ذلك ، أمرت بإنتاج Crystal Feigenbaum-Zvitanovich ، وهو تمثال زجاجي ثلاثي الأبعاد يصور تقييد الوظيفة g (z) على المستوى المركب.

كان حل المعادلة الوظيفية أمرًا صعبًا بعض الشيء ، حيث قام النقش بالليزر أولاً بتقسيم قطعتين من الزجاج ، لكن في النهاية تمكنت من تصنيع هذا الكائن وإرساله - وبعد عدة سنوات ، سُررت برؤيته على رف في شقة Mitchell:



في بعض الأحيان ، في محفوظاتي ، يذكر Mitchell من قِبل أشخاص آخرين ، عادةً بواسطة Predrag. في عام 2007 ، كتب لي بريدراج (بروح الدعابة المميزة):

لأخبار أخرى: التقيت للتو مع ميتشل ، يلتقي بأوديسي.

أنا لا أقصد خدمة مرافقة باهظة الثمن ، ولكن أوديسي هوميروس. تولى حساب موقع النجوم كدالة مع مقدرة 26000 سنة. يقول إن هيبارخوس كان يحسب كل هذا ذات مرة ، لكن الكنيسة الكاثوليكية تمكنت من تدمير جميع نسخ لوحاته ".

بتبرير صورته كرجل عصر النهضة ، كان ميتشل دائمًا مهتمًا جادًا بالتاريخ. في عام 2013 ، رداً على مقالتي حول لايبنتز ، قال ميتشل إنه كان من محبي لايبنتز منذ فترة المراهقة ، وأوضح:

"لم يكن لديجيوغير نيوتن ، فولتير ، أي فكرة عن جوهر الأحادية ، لذا لم أتمكن من تزوير" أفضل ما في العالمين المحتملين ". منذ فترة طويلة ، نشرت هذا كوسيلة شفهية لشرح عالمية 2 ^ن .

احتوى كتاب أعمال لبنيز الثاني عندما كان عمره 19 عامًا ، "على أساليب انعكاس المماس" ، أو شيء من هذا القبيل ، على اختراع طريقة الإيزوكلاين لحل المعادلات التفاضلية العادية. يبدأ لايبنز ونيوتن بالمعادلات التفاضلية ، بعد أن تلقيا بالفعل ترميزًا تفاضليًا. قصة مثيرة جدا للاهتمام. "

ومع ذلك ، فإن الفيزياء الرياضية كانت دائمًا معقلًا لحياة ميتشل الفكرية ، وإن كان ذلك على المستوى الشخصي أكثر من كونه جزءًا من عمله الأكاديمي. في مرحلة ما ، سألته ابنته الشابة ، وهو صغير جدًا ، عن سبب كون القمر ، الأقرب إلى الأفق ، أكبر. لقد كتب لها إجابة (مثل رسائل أولر إلى أميرة ألمانية) ، ثم أدرك أنه لم يكن متأكدًا من الإجابة ، وشرع في عدة سنوات من البحث في مجال البصريات والتصوير. وبمجرد وصوله إلى معهد ماساتشوستس للتكنولوجيا ، أصبح مهتمًا بعمل شبكية العين ، مستوحى من كتاب جيري ليتوين بعنوان "ماذا تقول عين الضفدع لعقل الضفدع".

أخبرني بذلك ، قائلاً إن النظرية المعتادة لتكوين الصورة خاطئة ، ولديه نظرية أفضل. لقد استخدم دائمًا حجم القمر كمثال ، لكنني لم أكن متأكدة مما إذا كانت هذه المشكلة تتعلق بالبصريات أو الإدراك. لم ينشر أبدًا أي أعمال متعلقة بهذا الموضوع ، على الرغم من أنه من حسن حظه أن مخطوطاته (وفقًا للشائعات ، كان يعد كتابًا) ، ونتيجة لذلك سوف يرون النور - إذا استطاع أي شخص آخر فهمها.

عندما زرت ميتشيل وجونيلا ، كانت لشققهم انطباعًا بوهيميًا - كانت هناك كتب وأوراق ولوحات وأشياء مختلفة متشابهة في كل مكان. وكان هناك طائر. كان كوكاتو ، وكان بصوت عال. لا أعرف من ولماذا أحضرها. لكنه كان مزعجا جدا. تم طرد ميتشيل وجونيلا من الشقة تقريبًا بسبب شكاوى الجيران حول الضوضاء ، وقادوا الطائر في النهاية إلى الأطباء. كما اكتشفت لاحقًا ، فإن المراجعة غير المتوقعة للخطة التي لم يتم تنفيذها مطلقًا لتطوير ألعاب الفيديو للحيوانات الأليفة ("عقل شخص آخر على كوكبنا") ، تعد الكوكاتو مخلوقات اجتماعية ، وتحتاج مثل هذه الحيوانات الأليفة بالتأكيد إلى "Twitter for cockatoo".



ونتيجة لذلك ، غادر جونيلا الأسرة ، ووفقًا للشائعات ، فقد كان بسبب الطائر.

آخر مرة التقينا فيها ميتشل شخصيا قبل بضع سنوات. لقد جئت أنا وابني كريستوفر لزيارته - وكان متحمسًا لميتشيل ، وتألقت عيناه ، وتحدث بسرعة وبشكل غامض قليلاً عن موضوع الفيزياء الرياضية لتكوين الصورة. وقال لصوت الكوكاتو من الغرفة المجاورة "إن عيون الطيور مبالغ فيها". الحفرة المركزية صغيرة جدا. عيونهم تعمل مثل التلسكوبات ".

وقال "إن أعين الأسماك هي الأفضل" ، موضحًا أن كل العيون ظهرت كنتيجة للتطور تحت الماء - وأن معماريها لم يتغير كثيرًا منذ ذلك الحين. وقال "الأسماك تبقي مجال الرؤية بأكمله في بؤرة التركيز ، على عكسنا". كان الساحر وغريب الأطوار وميتشل جدا.

لسنوات ، تحدثنا بشكل دوري على الهاتف ، وعادة في وقت متأخر من المساء. قبل بضعة أشهر ، قابلت بريدراج ، وأخبرته أنني فوجئت بأني لم أتحدث إلى ميتشل لفترة طويلة. وأوضح أن ميتشل كان مريضاً ، لكنه لم يخبر أحداً بذلك. قبل بضعة أسابيع ، في حوالي منتصف الليل ، أرسل إلي بريدراج رسالة بالبريد الإلكتروني بعنوان "ميتشل ميت" ، موضحًا أن ميتشل توفي في حوالي الساعة 8 مساءً وأرفقت صورة نموذجية لـ "ميتشل في نيويورك" بالرسالة:



على مر السنين ، طورت طقوسًا معينة بالنسبة لي - عندما سمعت عن وفاة صديق ، بدأت على الفور في البحث عنه في أرشيفي. واكتشفت فجأة أنه منذ بضع سنوات اتصل ميتشل بالبريد الصوتي الخاص بي ، والذي لم أكن أتوقع وجوده. حتى الآن يمكنني إعطاء ميتشل الفرصة لقول الكلمة الأخيرة .

وبالطبع ، اكتب الرقم الأخير: 4.66920160910299067185320382 ...