هل هناك فرصة موضوعية مثالية أم أنها نتيجة لجهلنا؟
الحياة لا يمكن التنبؤ بها ، والحوادث تحدث لنا طوال الوقت. يمكننا أن نقول أن الكون نفسه عرضي. ومع ذلك ، بطريقة ما ، يمكن لأعداد كبيرة من الأحداث العشوائية إنشاء أنماط واسعة النطاق يمكن للعلم التنبؤ بها. تبديد الحرارة والحركة البراونية هما مثالان فقط على مثل هذه الأحداث.
في الآونة الأخيرة ، دخلت العشوائية في موجز الأخبار: اتضح أن الأسطح العشوائية
لها ترتيب خفي ، وربما اقتربنا أيضًا من رؤية كيف
يولد الكمبيوتر الكمومي
العشوائية الكاملة . الحالة الأخيرة ، البحث عن العشوائية الكاملة ، مهمة لأن العشوائية تجلب عدم القدرة على التنبؤ ، وجميع محاولات التكنولوجيا غير الكمية لتحقيق ذلك بها عيب واحد مخفي: يتم تنفيذها باستخدام خوارزميات يمكن فك تشفيرها نظريًا. في هذا العمود ، سوف نتعلم كيفية إنشاء العشوائية وإلحاق الهزيمة بها في الحياة اليومية ، قبل الوصول إلى المستويات الفلسفية للجدل حول ما هو العشوائية الحقيقية.
لغز 1: مجموعات عشوائية
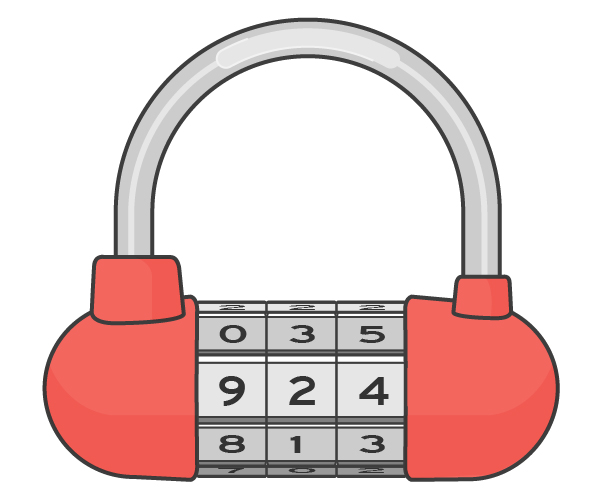
النظر في قفل رمز بسيط لدراجة ، على غرار الصورة أدناه. يحتوي على ثلاثة أقراص دوّارة ، يُظهر كل منها 10 أرقام بالترتيب. عندما يتم تدوير هذه الأقراص الثلاثة لإعطاء المجموعة المطلوبة - 924 - يفتح القفل. عندما تريد إغلاقها ، تحتاج إلى مزج الأرقام بحيث تكون بعيدة عن المجموعة المحددة. ولكن ماذا يعني "بعيد" في هذا السياق؟ إذا قمت بتحريك القرص قدر الإمكان بمقدار 5 وظائف ، فستحدد الرقم 479. ومع ذلك ، سيكون من السهل على المهاجم التعثر على هذا الموضع عن طريق الخطأ إذا قام ببساطة بتشغيل كل الأقراص الخمسة في نفس الوقت ورؤية ما إذا كان القفل يفتح. تخيل أن جهاز التكسير لديه الوقت لاختبار خمس مجموعات مختلفة. في كل حالة ، يحاول اللص المحتمل لدينا القلعة الخاصة بنا بعد أحد الإجراءات التالية (وفي حالة الفشل ، تقوم بإعادة القلعة إلى التكوين الأصلي):
- تدوير محرك واحد في عدد عشوائي من المواقف.
- تدوير قرصين في وقت واحد في عدد عشوائي من المواقف.
- قم بتدوير جميع الأقراص الثلاثة في نفس الوقت عن طريق عدد عشوائي من المواضع.
- تدوير قرصين في زوايا مختلفة.
- تدوير جميع الأقراص الثلاثة بشكل مختلف. ،
اللغز لدينا هو ما يلي: إذا كان رمز فتح القفل هو 924 ، أي مجموعة من الأرقام المختلطة ستكون الأكثر ثباتًا للمحاولات العشوائية لفتح القفل ، وكم عدد هذه المجموعات موجودة؟ ما هو احتمال الكشف عن الكود؟
لغز 2: من العشوائية إلى ترتيب في الألغاز
غالبًا ما يفاجئني مدى تشابه عملية حل اللغز مع التقدم العلمي. ننتقل من العشوائية إلى الترتيب ، ونضيف القطع ، وتغذي ثقتنا في صحة الحل مع كل قطعة مناسبة جديدة. في المهمة الثانية ، سنحاول إنشاء طريقة لقياس تقدمنا على الطريق من حالة مضطربة عشوائية إلى حل كامل منظم.
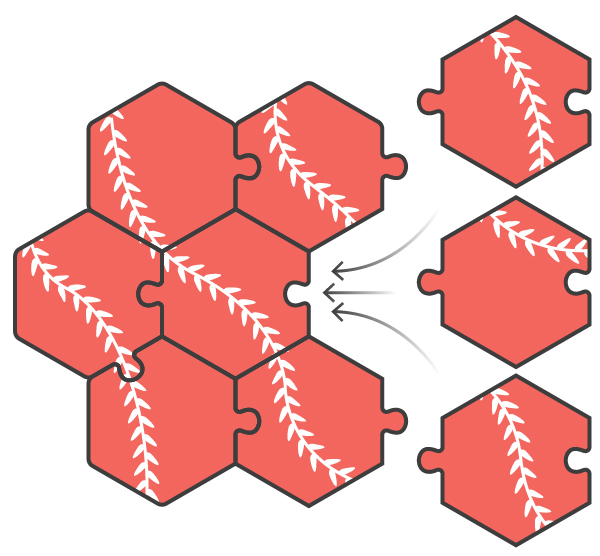
لنفترض أننا حلنا لغزًا يتكون من قطع سداسية - مثل أقراص العسل. صورة اللغز كرمة متعرجة. نظرًا لأن النموذج مكرر ومتشابه ذاتيًا ، لا يمكن ضمان أن قطعتين متجاورتين تتناسبان جسديًا مع بعضهما البعض ، حتى لو كانت تتناسب مع الصورة. لنفترض أن ثلاثة آخرين يمكنهم الذهاب إلى كل حافة قطعة معينة. لذلك ، عندما تلائم قطعتين بعضهما البعض في الصورة ، فإن احتمال ملاءمتها جسديًا سيكون 33.33٪. ومع ذلك ، إذا تمكنت من العثور على قطعة أخرى تناسب كل منهما ، أي أن لها ميزة واحدة مشتركة مع كل منهما ، فإن ثقتك في النجاح ستزداد. دعونا نحاول تقييم مقدار نموها.
- لقد وجدت ثلاث قطع يبدو أنها تتلاءم مع بعضها البعض للوهلة الأولى ، دون الإزاحة الواضحة لنمط ليانا عند حوافها المجاورة. ما هو مقياس ثقتك في الاختيار الصحيح للقطع؟
- لقد وجدت قطعة سداسية مركزية ، وستة تحيط بها ، ويبدو أنها تتزامن في الصورة. ما هو مقياس ثقتك في الاختيار الصحيح للقطع؟
كلما أصبحت مجموعات القطع أكبر ، زادت ثقتك في التجميع الصحيح. من المنطقي أن نفترض أن ثلاث مجموعات منعزلة ، والتي يوجد بها ما مجموعه سبع قطع متصلة ، لا يمكن مقارنتها بالمسدس المحاط الوحيد الموصوف أعلاه.
يحتوي الجزء الثالث من هذا اللغز على تصحيحات ، وهو محاولة لتحديد الفرق أعلاه. هل من الممكن الخروج بمقياس لدرجة إكمال اللغز الذي تم حله جزئيًا؟ يجب أن تسمح لك هذه الطريقة بتعيين رقم من 0 إلى 100 لأي لغز مجمّع جزئيًا يتكون من 10x10 مسدسات. يجب أن يشير هذا الرقم إلى درجة الإكمال ، مرتبطًا تقريبًا بنسبة الحالة الحالية للغز بالنسبة للإصدار النهائي.
لغز 3: هل الصدفة مثالية ممكنة؟
في هذا الجزء ، سأعطيك نوعًا مختلفًا من النقاش الشهير في أينشتاين-بوهر. يمكن للمشاركين في النقاش الانضمام إلى الفريقين E أو B.
يتفق كلا الفريقين على أن وجود آليات التوليد العشوائي أمر ممكن في العالم الكلي فقط لأننا لا نفهم القوى أو الخوارزميات التي تقوم عليها. إذا كنت تعرف كل القوى المؤثرة على قطعة نقود معدنية أو نرد ، إذا كان لديك قوة حسابية كافية ، فيمكنك التنبؤ بالنتيجة. لقد علمنا ، وفقًا لوجود آراء الفريق "ب" ، أن الأمر ليس كذلك في العالم الكوانتي - فالاحتمالات الكمومية يجب أن تكون موضوعية. ولكن هل هذا ممكن؟ هل يمكن أن يكون هناك بعض الآليات في عالم بلانك الكافي الذي يقرر أي من الخيارين المحتملين على قدم المساواة سيتم تنفيذه ، حتى لو لم تتح لنا الفرصة على الإطلاق لدراسة هذا المستوى؟ حتى لو كان كابوس آينشتاين النرد يلعب النرد حقيقيًا ، يجب أن يحتوي هذا الإله على نوع من الخوارزمية في رأسه يقرر كل خيار ، بغض النظر عن مدى الغرابة وغير المنطقية. ثم الفرصة ستكون مرة أخرى بسبب جهلنا. سيكون غير معروف فقط في الممارسة العملية ، وليس موضوعيا بشكل عشوائي.
الإجابة القياسية من الفريق (ب) هي أن العالم الكمومي هو ببساطة غريب جدًا في تطبيق القواعد التي تعلمناها من تجربتنا في التعامل مع العالم الكلي. ومع ذلك ، هناك نوعان من الشذوذ. من ناحية ، قد يكمن الغرابة في الاستحالة الجسدية للحركة بشكل أسرع من سرعة الضوء. قد توجد مثل هذه الغرابة ، وهذا سيعني فقط أننا نحتاج إلى إعادة النظر في فهمنا للقانون الفيزيائي في ظروف خاصة ، تمامًا كما راجع أينشتاين قانون إضافة سرعات نيوتن ، الذي أصبح خطأًا عند قيم كبيرة جدًا.
من ناحية أخرى ، قد يكون هناك شيء غريب من حيث الاستحالة المنطقية - مثل 2 + 2 يساوي 5. مثل هذه النتيجة مستحيلة في أي عالم. قد يجادل الفريق "هـ" بأن الفرصة المثالية والاحتمالات الموضوعية مستحيلة منطقياً. يجب ألا نقبلها ، ولكن بدلاً من ذلك يجب علينا إيجاد آليات مادية يمكنها شرح النتائج المرصودة ، بغض النظر عن قوانين الفيزياء الحالية التي قد تنتهكها.
أي فريق تنضم؟
ملاحظة: سيتم نشر الإجابات في وقت لاحق.