تحية!
في هذه "المقالة" ، أو بالأحرى في المقالة ، سأعرض طريقة بسيطة للغاية لأستمتع بمعرفة أساسيات اللاتكس والبيثون.
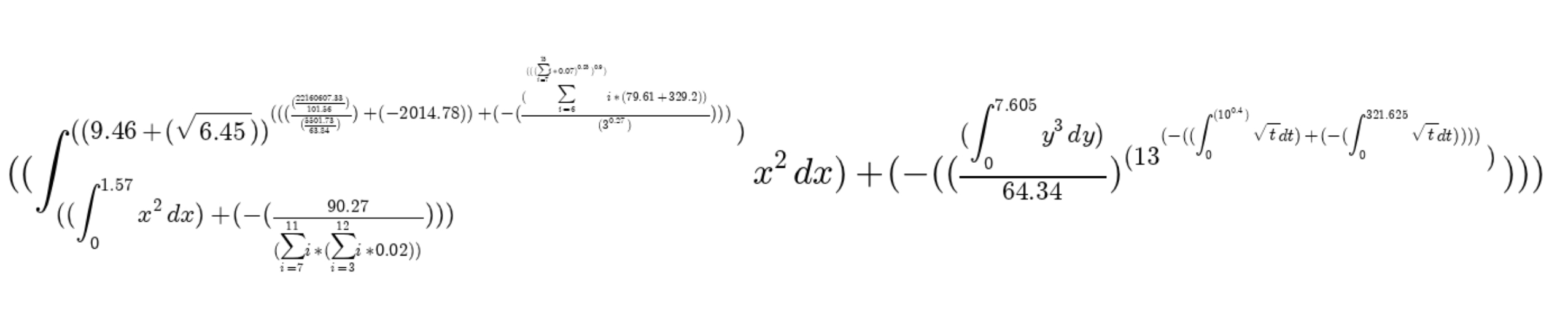
لماذا؟
حسنًا ، يمكنك إنشاء تعبيرات بسيطة يمكن للأطفال حسابها. أو تماما مثل ذلك. نعم ، على الأقل وضعت على خلفية ، إذا كنت متعصبا كما أنا.
كيف يكون هذا من المفترض أن تعمل؟
الفكرة بسيطة للغاية حقًا ، فبإمكان أي شخص أن يكتب مثل هذا البرنامج. نريد إنشاء تعبير مساوٍ لبعض الأرقام n (التي يدخلها المستخدم). يمكن استبدال أي رقم بتعبير حسابي ، على سبيل المثال ، 3 = 1 + 2. و 2 هو 4 / 2. هكذا أنشأنا 3 = 1 + 4/2. وبالمثل ، نقدم العديد من العمليات المختلفة ونلفها في LaTeX ، لغة الصيغة.
سوف تحتاج ...تجربة أسبوع واحد في بيثون و matplotlib. انا جاد
الآلية الرئيسية
نحتاج إلى تحليل التعبير للحصول على الأرقام من هناك. دعنا نسمي صفنا كمولد للمشاكل (كلنا نفتقده كثيرًا!)
import random from math import log import math import sys sys.setrecursionlimit(1000)
معنى دالة extract_nums هو الحصول على n أزواج من الأرقام (a ، b) ، حيث a هي موضع الحرف الأول ، b هو موضع آخر + 1.
على سبيل المثال ، إذا قمنا بتشغيل الكود التالي:
gen = ProblemGenerator() print(gen.extract_nums("13+256/355+25"))
سوف نرى:
[(0, 2), (3, 6), (7, 10), (11, 13)]
وهذا هو ، مجموعة tuple. (0 ، 2) يعني أن هناك رقمًا بين 0 (ضمني) و 2 (غير شامل).
الآن نود أن نجعل مشغلين مختلفين ، دعنا نبدأ بالضرب والجمع. أعلن ثلاث وظائف
def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b) return a + " * " + b
إن جوهر الدالة unmin ليس فقط تحويل كل الوسائط إلى سلاسل ، ولكن أيضًا إلى وضع علامة بين أحد المعامِلات إذا كانت أقل من الصفر. على سبيل المثال ، حصلنا على الأرقام a = 3 ، b = -4. إذا نكتب
a = 3 b = -4 a, b = unmin(a, b)
ثم = "3" ، ب = "(- 4)"
حسنًا ، بقية الوظائف واضحة: __c_sum تُرجع سلسلة من النموذج "13 + 4" ، و __c_mul "13 * 4".
يبقى الجمع بين هاتين القطعتين واستبدال كل رقم في التعبير بالتعبير.
أضف الكود التالي إلى ProblemGenerator:
class ProblemGenerator: ... def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e
تعقيد يأخذ بعض الأرقام ، وإرجاع سلسلة - تعبير معقد. على سبيل المثال ، إذا كتبنا:
gen = ProblemGenerator() gen.add_expander(__c_sum) print(gen.complexify(13))
نحصل على:
31.2 + (-18.2)
كيف يعمل __rxp__؟ نختار بشكل عشوائي موضع رقم من تعبير (على سبيل المثال ، إذا كان هناك تعبير "13 + 35/45" ، فلنفترض أننا حددنا (3 ، 5)) واستبدل هذا الرقم بتعبير يساوي هذا الرقم. وهذا هو ، أود أن:
"13 + 35/45" - رقم عشوائي (3 ، 5)
"13+" + "(12 + 23)" + "/ 45"
"13+ (12 + 23) / 45"
هكذا يعمل __rxp__
حسنًا ، يعمل randexpr بكل بساطة. على سبيل المثال ، إذا كان لدينا أربع خطوات ، فسيتم فتح التعبير كما يلي:
13 (5.62 + 7.38) ((20.63 + (-15.01)) + 7.38) ((20.63 + (-(67.5 + (-52.49)))) + 7.38) ((20.63 + (-((15.16 + 52.34) + (-52.49)))) + 7.38)
دعنا نحاول الجري:
gen = ProblemGenerator() gen.add_expander(__c_sum) gen.add_expander(__c_mul) exp = gen.randexpr(1, 5) print(exp)
النتيجة:
((6.63 + (56.62 + 16.8)) + (-((60.53 + 3.61) + 14.91)))
مطاط
الغريب ، أبسط ما تبقى. سنعلن عن عدد من مشغلي LaTeX المختلفين:
def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c
أضف جميع الوظائف إلى الجنرال:
gen = ProblemGenerator() gen.add_expander(__l_sum)
أخيرًا ، أضف ناتج النتيجة:
import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)
هذا كل شيء.
كود كامل import random from math import log import math import sys sys.setrecursionlimit(1000) class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)] def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b, acc=5) return a + " * " + b def __c_sub(num): a = num + 100 ** (random.random() * 2) b = (a - num) a, b = unmin(a, b) return a + " - " + b def __c_log(num): fr = random.randint(300, 500) a = math.e ** (num / fr) a, fr = unmin(a, fr, acc=5) return "log(" + a + ") * " + fr def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c gen = ProblemGenerator() gen.add_expander(__l_sum) gen.add_expander(__l_div) gen.add_expander(__l_pow) gen.add_expander(__l_sqrt) gen.add_expander(__l_int) gen.add_expander(__l_sig) import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)