حيرت فرضية "الحساسية" العديد من علماء الكمبيوتر البارزين ، لكن تبين أن أدلةها الجديدة بسيطة للغاية لدرجة أن أحد الباحثين تمكن من تقليصها إلى تغريدة واحدة
يضع
العمل المنشور هذا الصيف حدا لتاريخ ما يقرب من 30 عامًا من الفرضية المتعلقة ببنية اللبنات الأساسية لدارات الكمبيوتر. فرضت هذه الفرضية المتمثلة في "الحساسية" على حيرة العديد من علماء الكمبيوتر البارزين لسنوات ، ولكن اتضح أن برهانها الجديد بسيط للغاية لدرجة أن أحد الباحثين استطاع أن يختزلها إلى تغريدة واحدة.
وكتب سكوت آرونسون من جامعة تكساس في أوستن في مدونته: "كانت هذه الفرضية واحدة من أكثر المهام المفتوحة مزعجة ومخزية في جميع المجموعات التوافقية والمعلوماتية النظرية". وأضاف في رسالة بالبريد الإلكتروني: "قائمة الأشخاص الذين حاولوا إثبات ذلك وفشلوا في ذلك هي قائمة بأبرز الأشخاص في الرياضيات المنفصلة وعلوم الكمبيوتر النظرية".
ترتبط هذه الفرضية بوظائف Boolean - قواعد تحويل سلاسل البتات الواردة (الأصفار والأخرى) إلى بت واحد. إحدى هذه القواعد تنتج 1 عندما تكون كل البتات الواردة 1 و 0 خلاف ذلك ؛ تقوم قاعدة أخرى بإرجاع 0 إذا كان السطر يحتوي على عدد زوجي من الوحدات ، و 1 في حالة أخرى. وقال
روكو سينديو من جامعة كولومبيا إن كل دارة كمبيوتر عبارة عن مزيج من وظائف Boolean ، مما يجعلها "مادة بناء كل ما يتم في علوم الكمبيوتر".
على مر السنين ، تم تطوير العديد من الطرق في علوم الكمبيوتر لقياس تعقيد وظيفة بوولية معينة. يستخدم كل مقياس جانبه الخاص بكيفية تحديد معلومات سطر الإدخال بت الإخراج. على سبيل المثال ، تشير "حساسية" دالة بوولية ، تقريبًا ، إلى احتمال أن يؤدي تغيير بت واحد في الإدخال إلى تغيير البت في الإخراج. و "تعقيد الطلب" يحسب عدد البتات الواردة التي تحتاج إلى طلب لمعرفة يقين ما ستكون عليه المنتهية ولايته.
يعطي كل قياس وجهة نظره الفريدة الخاصة بهيكل الوظيفة المنطقية. ومع ذلك ، وجد علماء الكمبيوتر أن جميع هذه التدابير تقريبًا تتوافق مع منصة عالمية ، وأنه من خلال قيمة واحد منها ، يمكن للمرء تقريبًا تقدير أهمية الآخرين. ولم يندرج في هذا المخطط سوى مقياس واحد من التعقيد: الحساسية.
في عام 1992 ، اقترح نعوم نيسان من الجامعة العبرية في القدس وماريو زيجيد ، اللذين يعملان الآن في جامعة روتجرز ، أن الحساسية لا تزال تلائم هذا المنبر. لكن لا أحد يستطيع أن يثبت ذلك. قال سينديو: "كان هذا السؤال ، كما أعتقد ، رائعًا في مجال دراسة الوظائف المنطقية".
وقال ريان أودونيل من جامعة كارنيجي ميلون "كتب الناس أعمالًا طويلة ومعقدة يحاولون إحراز تقدم ضئيل للغاية".
والآن ، أثبت
هاو هوانغ ، وهو عالم رياضيات من جامعة إيموري ، فرضية الحساسية بمساعدة إثبات رائع ولكنه أساسي من صفحتين يتعلق بمجموعات من النقاط على المكعبات. كتبت كلير ماثيو من مركز الدولة الفرنسي للبحث العلمي في مقابلة على سكايب: "إنها جميلة ، مثل اللؤلؤة الثمينة".
دعا آرونسون وأودونيل عمل خوان "كتاب" كدليل على فرضية الحساسية ، في إشارة إلى مفهوم "الكتاب السماوي" لبال إيردوس ، الذي يكتب فيه الله براهين مثالية لكل نظرية. "من الصعب بالنسبة لي أن أتخيل أنه حتى الله يعرف دليلًا أبسط على نظرية الحساسية" ، كتب آرونسون.
موضوع حساس
قال ماثيو ، تخيل أنك تملأ نموذجًا بأسئلة في نموذج طلب القرض المصرفي ، الإجابات التي يمكن أن تكون بنعم / لا. عند الانتهاء ، سيقوم المصرف بتقييم النتائج ويخبرك إذا كنت مناسبًا للحصول على قرض. هذه العملية هي وظيفة منطقية: إجاباتك هي بتات واردة ، وقرار المصرف قد انتهى.
إذا تم رفض طلبك ، فيمكنك التفكير فيما إذا كان بإمكانك تغيير النتيجة عن طريق الكذب في سؤال واحد - ربما بالقول إنك تكسب أكثر من 50000 دولار في السنة ، على الرغم من أن هذا ليس كذلك. إذا غيرت هذه الكذبة نتيجة الاعتبار ، فسيطلق علماء الكمبيوتر على هذه الوظيفة المنطقية "حساسية" لقيمة جزء معين. على سبيل المثال ، إذا كنت تستطيع الاستلقاء في أحد الأماكن السبعة ، وفي كل مرة غيرت النتيجة ، فستكون حساسية الوظيفة المنطقية لتقييم طلب القرض سبعة.
يعرّف علماء الكمبيوتر الحساسية الكلية لوظيفة بوولية باعتبارها أعلى قيمة حساسية لجميع الخيارات الممكنة لملء تطبيق ما. بمعنى ما ، يحسب هذا التدبير عدد المشكلات التي ستكون مهمة حقًا في معظم الحالات الحدودية - في التطبيقات ، والتي يتم تغيير نتائجه بسهولة إذا تم تعديل التطبيقات نفسها قليلاً.
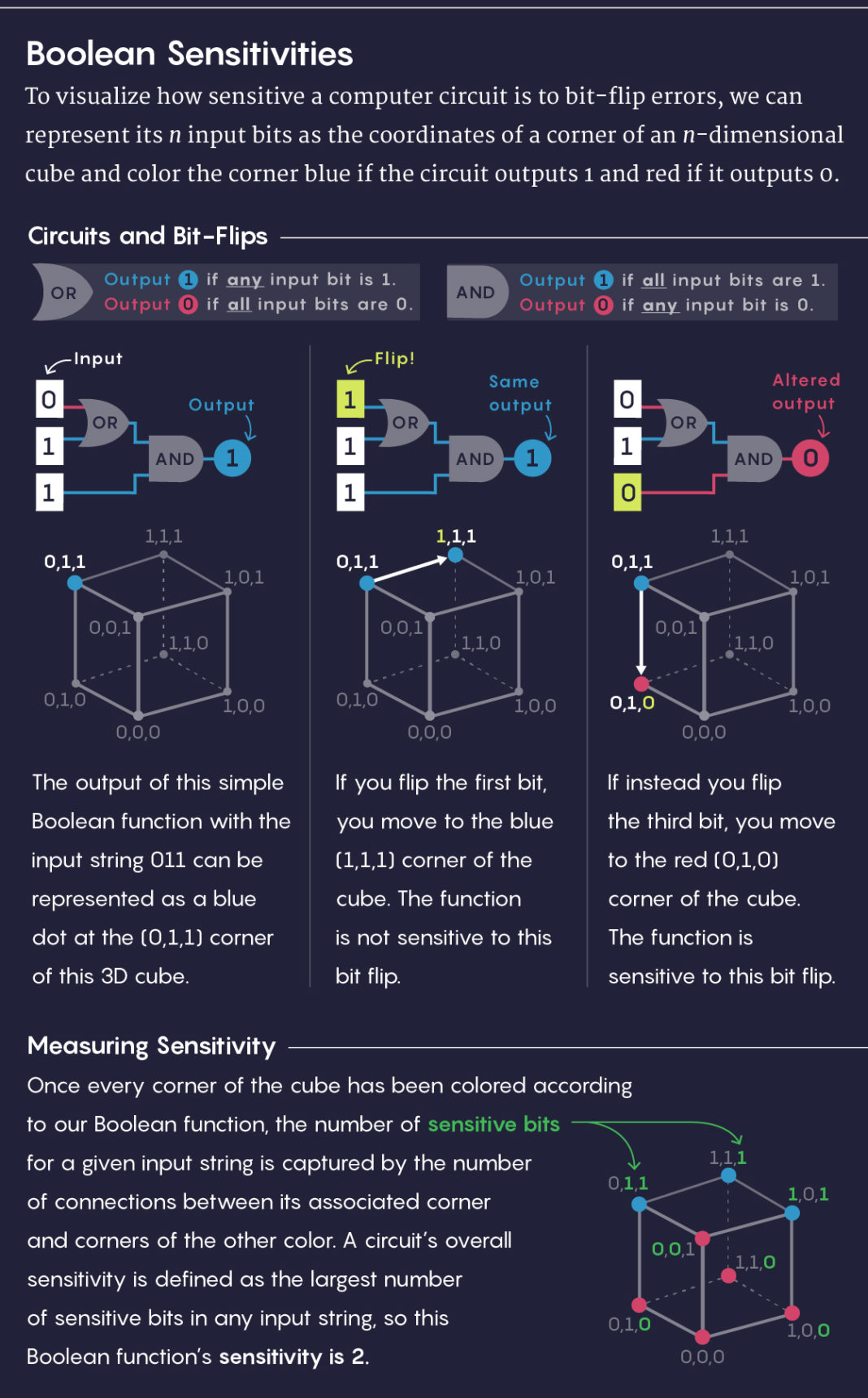 لتصور حساسية الدائرة للأخطاء مع عكس البتات ، يمكن تمثيل البتات الواردة كإحداثيات لرؤوس المكعب ذي الأبعاد n. سنقوم بتلوين قمة الرأس الزرقاء إذا كان المسار ينتج 1 والأحمر إذا كانت 0.
لتصور حساسية الدائرة للأخطاء مع عكس البتات ، يمكن تمثيل البتات الواردة كإحداثيات لرؤوس المكعب ذي الأبعاد n. سنقوم بتلوين قمة الرأس الزرقاء إذا كان المسار ينتج 1 والأحمر إذا كانت 0.
في منتصف اليسار: يمكن تمثيل مخرجات دالة منطقية بسيطة مع إدخال 011 بنقطة زرقاء في أعلى المكعب (0،1،1).
المركز: عند إلقاء الضوء على الجزء الأول ، سننتقل إلى القمة الزرقاء للمكعب (1،1،1). الوظيفة ليست حساسة لانقلاب هذا البت.
في المنتصف الأيمن: عند تشغيل البت الثالث ، سننتقل إلى الجزء العلوي الأحمر من المكعب (0،1،0). وظيفة حساسة لعكس هذا الشيء.
بعد أن قمت بتلوين جميع رؤوس المكعب ، نحصل على عدد البتات الحساسة لخط وارد معين يساوي عدد الاتصالات بين الرأس المتوافق والرؤوس بلون مختلف. تُعرَّف حساسية الحلقة بأنها أكبر عدد من البتات الحساسة في أي خط إدخال ، وبالتالي فإن هذه الوظيفة لها حساسية 2.تعد الحساسية عادةً واحدة من أسهل التدابير لحساب التعقيد ، ولكنها ليست على الإطلاق تدبير توضيحي بسيط. على سبيل المثال ، يمكن أن يبدأ مصرفينا ، بدلاً من إعطائك نموذج لملء ، بسؤال واحد ، ثم يستخدم إجابتك لتحديد السؤال الذي يجب طرحه بعد ذلك. أكبر عدد من الأسئلة التي سيحتاج المصرف إلى طرحها قبل التوصل إلى قرار هو مدى تعقيد طلب وظيفة منطقية.
يظهر هذا الإجراء في مجموعة متنوعة من المواقف - على سبيل المثال ، قد يرغب الطبيب في إرسال المريض لجمع أقل عدد ممكن من الاختبارات لإجراء تشخيص ، أو قد يرغب خبير في التعلم الآلي في إنشاء خوارزمية تدرس أقل عدد ممكن من خصائص الكائن قبل ذلك وقال انه سوف يكون قادرا على تصنيفها بشكل صحيح. وقال أودونيل: "في العديد من المواقف - التشخيص أو التدريب - تحب القاعدة الأساسية أن تكون درجة تعقيد الاستعلام منخفضة".
من بين التدابير الأخرى ، البحث عن أبسط طريقة لكتابة دالة منطقية في شكل تعبير رياضي ، أو لحساب عدد الإجابات التي سيضطر المصرفي إلى إظهارها من أجل إثبات أن التطبيق قد تمت معالجته بشكل صحيح. هناك أيضًا اختلاف في تعقيد الاستعلام من فيزياء الكم ، عندما يسأل المصرفي "تراكب" لعدة أسئلة في نفس الوقت. لفهم العلاقة بين هذا التدبير ومقاييس التعقيد الأخرى ، يفهم الباحثون بشكل أفضل حدود الخوارزميات الكمومية.
لقد أثبت علماء الكمبيوتر أن هناك علاقة وثيقة بين كل هذه التدابير ، باستثناء الحساسية. وبشكل أكثر تحديدا ، وجدوا أنهم مرتبطون ببعضهم البعض بالاعتماد على كثير الحدود - على سبيل المثال ، يمكن التعبير عن أحد المقاييس كمربع أو مكعب آخر. والحساسية فقط قاومت بعناد ، عدم الرغبة في الاندماج في مخطط التصنيف المريح هذا. اشتبه العديد من الباحثين في أنه ينبغي أن يكون مناسبًا لها ، لكنهم لم يتمكنوا من إثبات عدم وجود وظائف بوولية غريبة ترتبط حساسيتها بتدابير أخرى ليس بالعدد متعدد الحدود بل بالاعتماد الأسي ، مما يعني في هذه الحالة أن مقياس الحساسية هو في الأساس أصغر من البقية.
وقال آرونسون "هذا السؤال أبقى الناس مستيقظين لمدة 30 عامًا".
ركن الحل
اكتشف خوان هذه الفرضية في نهاية عام 2012 ، في مأدبة عشاء مع عالم الرياضيات
مايكل ساكس من معهد الدراسات المتقدمة ، حيث كان خوان في مرحلة ما بعد الدكتوراه. كان مفتونًا على الفور بساطة الفرضية وأناقتها. وقال "ومنذ تلك اللحظة أصبحت مهووسًا بأفكار عنها".
أضاف خوان فرضية الحساسية إلى "القائمة السرية" للمشاكل التي كان مهتمًا بها ، وعندما تعرّف على بعض الأدوات الرياضية الجديدة ، تساءل عما إذا كان بإمكانه مساعدته. وقال "في كل مرة بعد نشر عمل آخر ، عدت إلى هذه المهمة". "بالطبع ، خصصت الوقت والطاقة للعمل على مهام أكثر واقعية."
 هاو هوانغ في عطلة الأخيرة في لشبونة
هاو هوانغ في عطلة الأخيرة في لشبونةعرف خوان ، مثل الكثيرين في مجتمع الأبحاث ، أن فرضية الحساسية يمكن إثباتها إذا كان بإمكان علماء الرياضيات إثبات فرضية أخرى ذات شرط أبسط فيما يتعلق بمجموعة من النقاط على مكعبات ذات أبعاد مختلفة. هناك طريقة طبيعية للانتقال من سلسلة من الأصفار والأخرى إلى نقطة على مكعب أبعاد n: استخدم فقط n bits كإحداثيات لتلك النقطة.
على سبيل المثال ، تتطابق أربعة خطوط ثنائية البتات - 00 و 01 و 10 و 11 - مع الزوايا الأربع للمربع على مستوى ثنائي الأبعاد: (0،0) و (0،1) و (1،0) و (1،1). وبالمثل ، تتوافق ثمانية سلاسل ثلاثية البتات مع ثمان زوايا لمكعب ثلاثي الأبعاد ، وما إلى ذلك ، لأبعاد أعلى. يمكن اعتبار دالة Boolean قاعدة لتلوين زوايا المكعب هذه بلونين مختلفين (على سبيل المثال ، الأحمر لـ 0 والأزرق لـ 1).
في عام 1992 ،
أدرك كريج جوتسمان ، الذي يعمل حاليًا في معهد نيوجيرزي للتكنولوجيا وناتي لينيال من الجامعة العبرية ، أن دليل فرضية الحساسية يمكن اختزاله إلى إجابة سؤال بسيط حول مكعبات ذات أبعاد مختلفة: إذا كنت تأخذ أي مجموعة تتكون من أكثر من نصف رؤوس مكعبات ، وتلوينها باللون الأحمر ، هل من الضروري العثور على نقطة حمراء متصلة بالعديد من النقاط الحمراء الأخرى (بواسطة النقاط "المتصلة" نعني أن هناك رأسان متصلان بحافة مشتركة ، ولا يقعان قياس انحرافي).
إذا كانت مجموعتنا الفرعية تحتوي على نصف رؤوس المكعب تمامًا ، فقد لا تكون متصلة ببعضها البعض. على سبيل المثال ، من بين الزوايا الثمانية لمكعب ثلاثي الأبعاد هناك أربع نقاط ،
(0،0،0) و (1،1،0) و (1،0،1) و (0،1،1) تقع قطريًا عن بعضها البعض. ولكن بمجرد أن يتحول أكثر من نصف رؤوس أي مكعب من أي بُعد إلى اللون الأحمر ، يجب ربط النقاط الحمراء فيما بينها. والسؤال هو كيف يتم توزيع هذه الاتصالات؟ هل سيكون هناك واحد على الأقل من هذه القمم مع المزيد من الاتصالات؟
في عام 2013 ، بدأ خوان في التفكير في أن أفضل طريقة لفهم هذه المشكلة هي على الأرجح استخدام الطريقة القياسية لتمثيل الشبكة باستخدام مصفوفة تتبع النقاط المتصلة ، ثم تدرس الكثير من الأرقام تسمى القيم الذاتية للمصفوفة. لمدة خمس سنوات عاد بشكل دوري لهذه الفكرة ، ولكن دون جدوى. "على الأقل بسبب ما فكرت به قبل الذهاب إلى الفراش ، كان من الأسهل بالنسبة لي النوم لعدة ليالٍ" ، علق على مدونة Aaronson.
ثم في عام 2018 ، فكر خوان في استخدام نظرية كوشي البديلة ، وهي عبارة عن بيان رياضي قبل 200 عام ، يربط القيم الذاتية لمصفوفة بمصفوفة فرعية ، مما يجعلها ربما أداة مثالية لدراسة العلاقة بين المكعب ومجموعة فرعية من رؤوسها. قرر خوان طلب منحة من مؤسسة العلوم الحكومية لمواصلة استكشاف هذه الفكرة.
ثم ، في الشهر الماضي ، أثناء وجوده في فندق في مدريد وملء طلب الحصول على منحة ، أدرك فجأة أنه يمكن أن يمدد استخدام هذا النهج إلى النهاية ، ببساطة تغيير علامات بعض الأرقام من المصفوفة. وبهذه الطريقة ، كان قادرًا على إثبات أنه في أي مجموعة من أكثر من نصف رؤوس المكعب الأبعاد ستكون هناك نقطة مرتبطة بنقاط أخرى على الأقل - وفرضية الحساسية تتبع مباشرة من هذه النتيجة.
عندما تلقى ماثيو عمل خوان في البريد ، كان رد فعلها الأول هو "عفوا". "عندما توجد مهمة لمدة 30 عامًا ويعرف الجميع عنها ، يجب أن يكون دليلها طويلًا ومعقدًا جدًا أو عميقًا للغاية." فتحت الملف مع العمل ، متوقعة أنها لن تفهم شيئًا.
ومع ذلك ، كان الدليل بسيطًا بما فيه الكفاية حتى يتمكن ماثيو وغيره من الباحثين من هضمه في جلسة واحدة. وكتبت على سكايب "أعتقد أنه في هذا الخريف ، سيخبره الطلاب كجزء من محاضرة واحدة في دورة كل ماجستير في الدمج".
اتضح أن نتيجة خوان كانت أقوى من اللازم لإثبات هذه الفرضية ، وينبغي أن تعطينا هذه القوة أفكارًا جديدة حول تدابير التعقيد. "لقد تمت إضافته إلى مجموعة أدواتنا وقد تساعد في الإجابة على الأسئلة الأخرى المتعلقة بوظائف Boolean" ، قال Cenedio.
لكن الأهم من ذلك أن نتيجة خوان تسمح لنا بوقف كل المخاوف بشأن ما إذا كانت الحساسية غريبة بعض الشيء في عالم تدابير التعقيد ، كما قال سينديو. "أعتقد أنه في المساء ، ومعرفة هذه النتائج ، تمكن الكثيرون من النوم بسلام".