اللعب بأعداد معقدة

تحية!

مقال آخر. هذه المرة لنلعب بالأرقام المعقدة ، مع الصيغ والتصور الخاصة بهم.

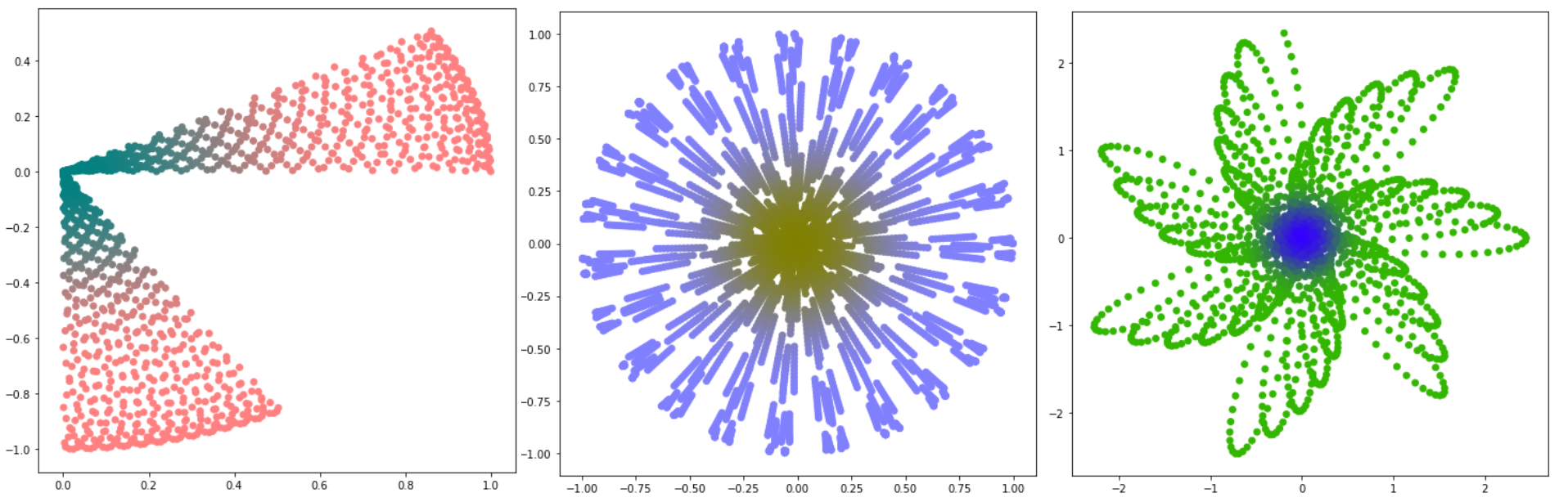
فكرة

الرقم المركب هو امتداد معين للرقم الحقيقي ، في الواقع عبارة عن متجه يتم تعريف مجموعة كاملة من البديهيات به. يمكن كتابة أي رقم معقد (وبالتالي حقيقي) كـ $$$z = a + bi$حيث a هو الجزء الحقيقي ، b هو الجزء التخيلي ، i هو أصل المعادلة $$$x ^ {2} = - 1 دولا$. يتم تعريف العديد من العمليات لذلك ، والتي يتم تعريفها لرقم حقيقي ، على سبيل المثال ، $$$z_1 + z_2 = a_1 + a_2 + (b_1 + b_2) i$. ومن المثير للاهتمام ، إذا قمت بإجراء عمليات مختلفة معهم ، فانتقل إلى السلطة ، واضرب ، وما إلى ذلك ، ثم خذها $$$Re (z)$(الجزء الحقيقي) للمحور الثور ، و $$$Im (z)$(جزء وهمي) بالنسبة لمحور Oy ، يمكنك الحصول على صور مضحكة.

بالمناسبة ، لقد توصلت بنفسي إلى كل الصيغ التالية.

وظيفة التصور

روتين. الوظيفة ، والتي وفقًا لهذه الدالة التكرارية ، توجه كل شيء في الحقل:

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() 

تعتمد جميع وظائفنا على معلمتين A و B. علاوة على ذلك ، فإننا نكررها على B من الداخل () ، و A هي المعلمة العامة للوظيفة.

وظيفة الضفيرة

$$

$$f (A، B) = Bsin (B) * e ^ {iBcos (A)}$$

إعلانها في الثعبان:

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

والركض

 A = 121.5 vis(A, func_1, step=0.1) 

والنتيجة لـ A = 121.5:



ولأ = 221.5:



لاحظ أن هذه الأرقام لا تتبع من حساب أي جزء لا يتجزأ محدد على سلسة متعددة الكلمات وغيرها من الكلمات الذكية لا معنى لها في هذا السياق. هذه أرقام عشوائية حقًا ، ولا يزال هناك ما لا نهاية تمامًا للألف مختلفة ، ونتيجة لذلك يتم الحصول على الجمال.

تحتاج إلى الطلاء

نعلن عن وظيفة اللون (مثل هذه الوظيفة التي تُرجع مجموعة من ثلاثة أرقام في الإحداثيات):

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) 

اختر المعلمة العشوائية A ، فليكن 149:

 vis(149, func_1, step=0.1, c=color_1) 

وظيفة الاوز

يتم وصف الأوز على النحو التالي:

$$

$$f (A، B) = cos (B) sin (B) * B * e ^ {iBcos (A)}$$

إعلان بايثون:

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

نتائجه لـ A = 106:

وظيفة Focaccia

$$

$$f (A، B) = cos (B (A + 1)) * e ^ {iBcos (A)}$$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) 

 vis(246, func_3, step=0.1, c=color_2) 

 vis(246, func_3, step=0.1, c=color_2) 

وظيفة بلا عنوان

$$

$$f (A، B) = Bsin (A + B) * e ^ {iBsin (A)}$$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3) 

 vis(179, func_4, step=0.1, c=color_3) 

صيغة الجمال

$$

$$f (A، B) = cos (B (A + 1)) ^ {\ frac {3} {2}} * e ^ {iBcos (A)}$$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) 

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4) 

 vis(350, func_5, step=0.1, c=color_4) 

هذا كل شيء الآن.