عند مناقشة المقال السابق حول
التصميم الموجه للطراز ، ظهر سؤال معقول: إذا استخدمنا بيانات التجربة ، ولكن هل من الممكن القيام بذلك بشكل أسهل ، ووضع البيانات في "تعريف النظام" والحصول على طراز الكائن دون عناء مع الفيزياء على الإطلاق؟ دون دراسة جميع أنواع الصيغ متعددة الطوابق من Navier-Stokes و Bernoulli وغيرها من بوصلات الفرجار مع Rabinovichi؟ اختبرنا الكائن - حصلت على النتيجة.
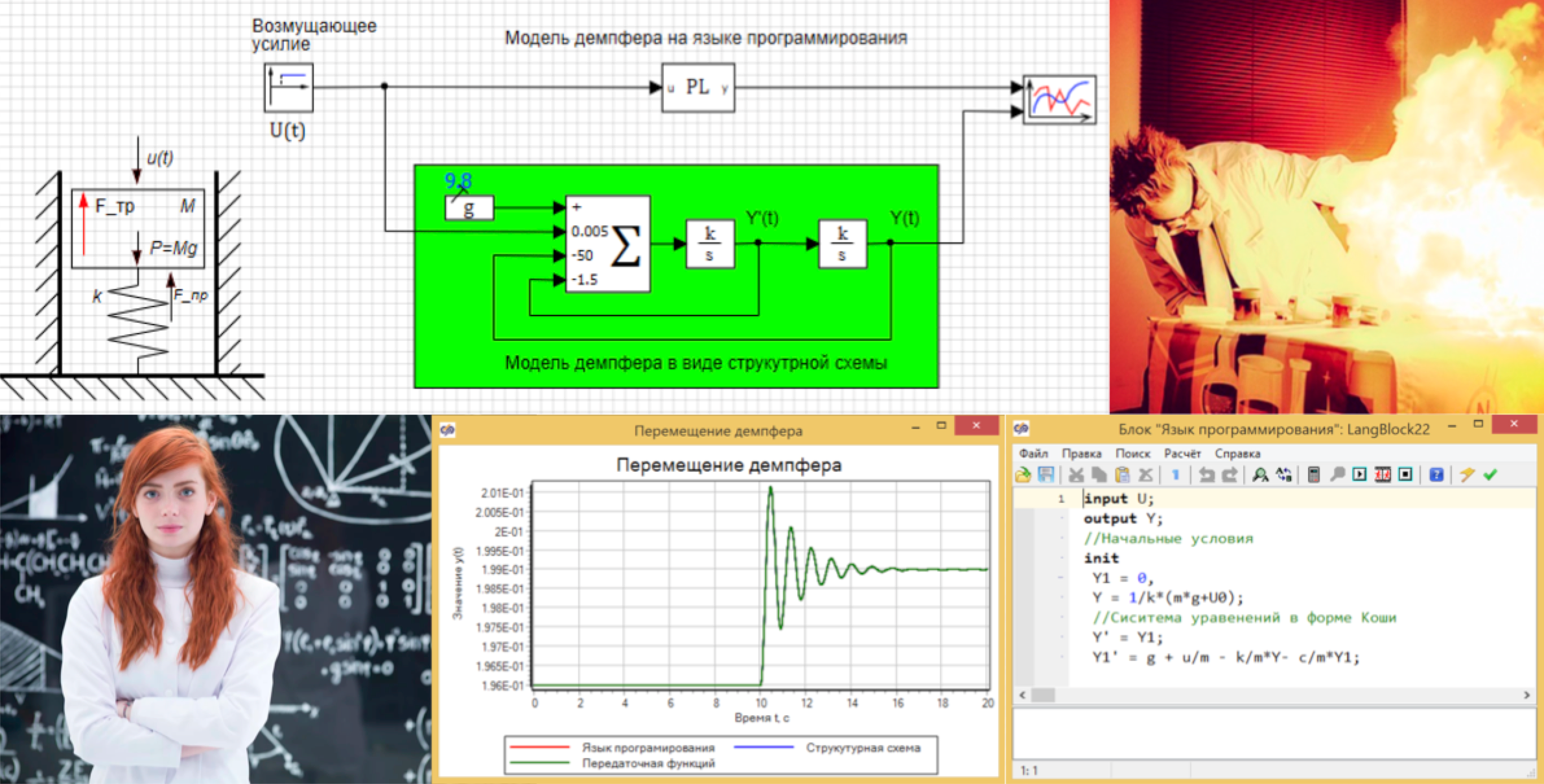
قدمنا نموذج صاروخ FAU2 كدالة نقل واحدة ،
يمكنك رؤيته هنا ... ويبدو أن كل شيء قد نجح. لماذا نحتاج أولاً إلى دراسة التحليل الرياضي والتفاضل والتكامل التفاضلي عندما يكون هناك زر سحري يحصل على النموذج من الاختبارات؟
في الواقع ، يمكن تطبيق هذا النهج ، لكن هذا يتطلب شرطين:
- يجب أن يكون الكائن بالفعل (غير مناسب للكائنات المصممة).
- يجب أن تكون بيانات القياس كاملة وموثوقة.
في أي حالات أخرى - "لقد أرادوا الأفضل ، واتضح كما هو الحال دائمًا" (ج).
على سبيل المثال ، في
هذه المقالة حول محاكاة محرك كهربائي ، يتبين أنه "بالنسبة لقيمة عتبة معينة من دقة أدوات القياس ، يصبح طراز محرك الأقراص غير معروف ، مما يؤدي إلى فقدان إمكانية التحكم وعدم القدرة على التشخيص"
في نفس المقالة ، سنقوم بتحليل سحر وسحر إنشاء نماذج في شكل وظائف نقل من TAU ، ومن ثم سننفذ جلسة لفضح هذا السحر.
لذلك أولا السحر
لنأخذ مثالا بسيطا. لدينا نموذج المثبط الميكانيكية. هذا مكبس في زنبرك ، يتحرك داخل الاسطوانة ، يمكنه التحرك لأعلى ولأسفل. موقفها هو الوظيفة Y (t) التي تهمنا ، والقوة المزعجة (U (t)) تعمل عليها من الأعلى ، وقوة الاحتكاك اللزج تعمل على جدران المكبس. (انظر الشكل 1)
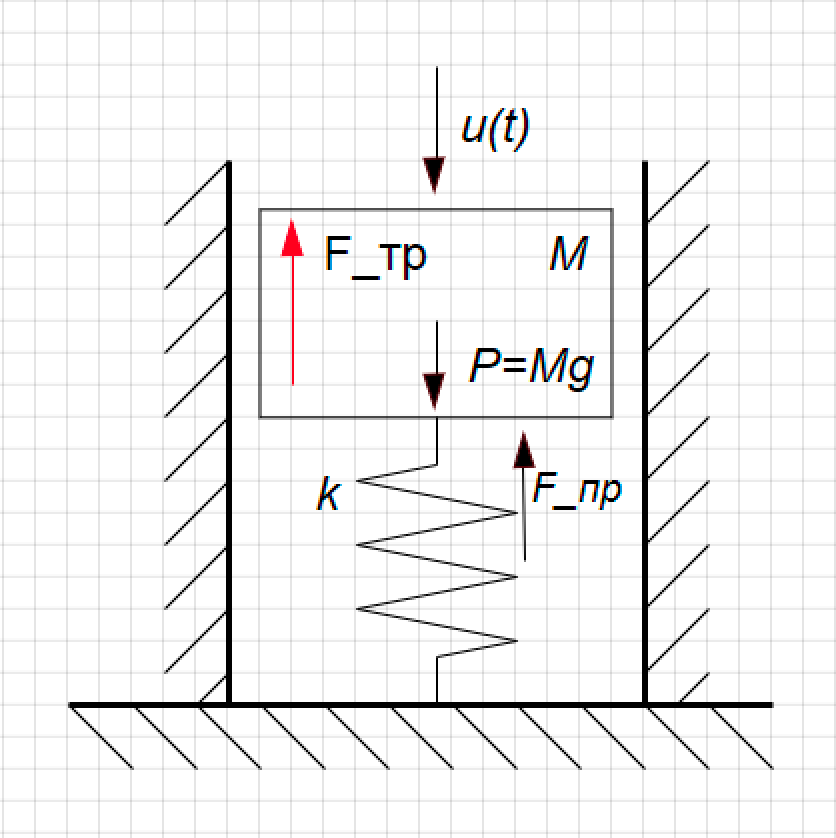الشكل 1. تصميم لامتصاص الصدمات.نستمد وظيفة النقل لهذا الرابط.
يمكن لأولئك Jedi الذين لديهم دراية بالفعل بسحر وظائف النقل أن يتخطوا هذا الجزء ويستعدوا للكشف عن السحر ، وبالنسبة لل Padawans الشباب سنكشف عن التكنولوجيا الكاملة للحصول على معادلات ديناميكية.
وفقًا لقانون نيوتن الثاني ، فإن تسارع الجسم يتناسب مع مجموع القوى المؤثرة على الجسم:
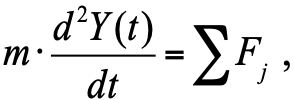
، (1)
حيث
m هو وزن الجسم ؛
F j - القوى المؤثرة على الجسم (مكبس المثبط).
استبدال في المعادلة (1) جميع القوى وفقا لشكل. 1 ، لدينا:
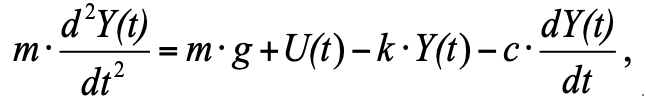
(2)
حيث:
Y (t) هو موضع المكبس ؛
P = m ∙ g - الجاذبية ؛
F_pr = k ∙ Y (t) - قوة مقاومة النابض ؛
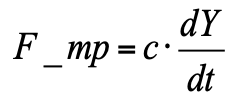
- قوة الاحتكاك اللزج (تتناسب مع سرعة المكبس).
أبعاد القوى والمعاملات المدرجة في المعادلة (2):
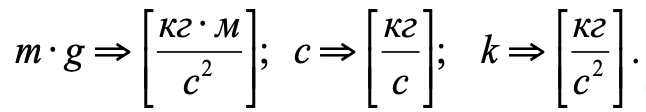
نعتقد أنه في وقت الصفر يكون المكبس في حالة توازن. إذن الموضع الأولي للمكبس هو y
0 في التوازن ، حيث السرعة والتسارع 0 ، يمكن حسابها من المعادلة 2.
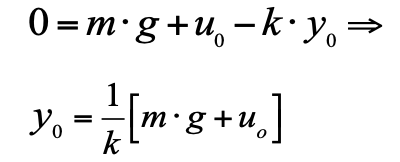
تتيح لك هذه المعادلة حساب الموضع الذي سيكون عليه المكبس بأحمال مختلفة. هذه السمة الساكنة: القوة المطبقة - النزوح المستلم. مظهره لنظامنا بسيط للغاية (انظر الشكل 2):
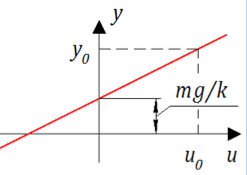الشكل 2. سمة ثابتة من المثبط.يبدو أنه هنا السعادة - خط بسيط ، عندما طبقت القوة ، تلقى النزوح. ولكن كان هناك! نحن لسنا مهتمين بالوضع النهائي للمكبس ، ولكن في عملية الانتقال من حالة إلى أخرى.
لتحليل العملية المؤقتة ، تم إنشاء نظرية التحكم التلقائي في TAU. وفقًا لـ "تقنية نموذجية لإنشاء نماذج" وفقًا لهذه النظرية ، يُقترح النظر في النظام ليس في القيم المطلقة ، ولكن في الانحرافات عن حالة التوازن. مثل هذا البيان يبسط الحل والبناء. وفي الحقيقة ، إذا استبدلنا القيم المطلقة بالانحرافات ، فسنحصل على:
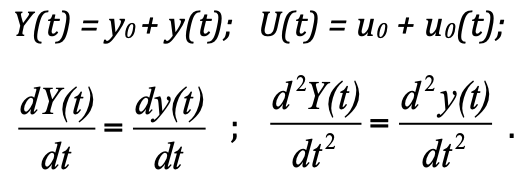F_pr = k ∙ (y 0 + y (t)) = k ∙ y 0 + k ∙ y (t) هي قوة مقاومة الربيع ؛
- قوة الاحتكاك.
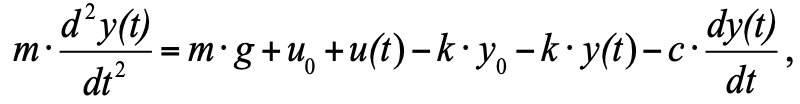
لكن بما أننا قبلنا أنه في اللحظة الأولى لدينا حالة توازن ، ومجموع القوى الثلاث في حالة التوازن هو صفر ، يمكننا إزالتها من المعادلة ، ونتيجة لذلك نحصل على:
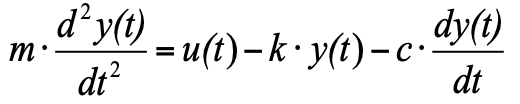
(4)
من أجل ترجمة المعادلة إلى النموذج وفقًا لقانون TAU ، تحتاج إلى تقسيم المعادلة بأكملها على k بحيث يكون المعامل y ، وقيمة متغير الإخراج تساوي 1 ، ونقل العوامل التي تحتوي على قيم إخراج
y (t) إلى الجانب الأيمن وقيم الإدخال إلى الجانب الأيسر التأثيرات
u (t) :
(5)
يمكن بالفعل كتابة هذه المعادلة في شكل عامل التشغيل:
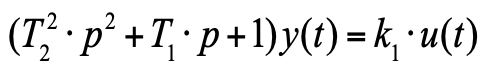
(6)
حيث:
p = d / dt هو عامل التمايز. لاحظ أن أبعاد المعاملات لها البعد ومعنى الثوابت الزمنية:
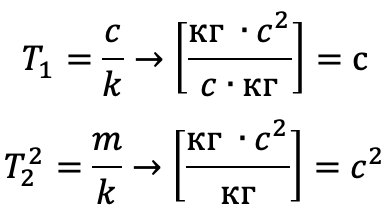
دالة النقل لمثل هذه المعادلة [6] لها الشكل:
الآن ، أمام عينيك ، حصلنا على وظيفة النقل في شكل كتلة من معادلات الفيزياء ، وعلاوة على ذلك ، فإن الكتلة الناتجة هي رابط تذبذب قياسي من TAU.
بالنسبة لي شخصيا ، فإن السحر هنا هو المظهر السحري للخصائص الثابتة ، وأجزاء من النظام ، وكتلة المكبس ، ومرونة الزنبرك ، والاحتكاك على الجدران) للكائن الذي ظهر بطريقة سحرية سمة مؤقتة للعابرين في النظام
تحقق من الصيغ مع النموذج
كما علمني
مكسيم أندرييف ، عند إنشاء نماذج ديناميكية "النهاية هي رأس كل شيء!" (
انظر هنا المبدأ الثاني للنمذجة - "البدء من النهاية" ):
وفي نهاية الوظيفة ، لدينا حركة.
لذلك ، تخيل المعادلة 2 في شكل كوشي ، للتحرك.
شكل كوشي هو عندما تكون على اليسار مشتقات من الوظائف التي تهمنا ، على اليمين عبارة عن تعبيرات لحسابها. نظرًا لأن المشتق في المعادلة من الدرجة الثانية ، حيث يقدم متغيرًا جديدًا Y1 - معدل تغيير الموضع (سرعة الإزاحة) ، نحصل على نظام من معادلتين في شكل كوشي:
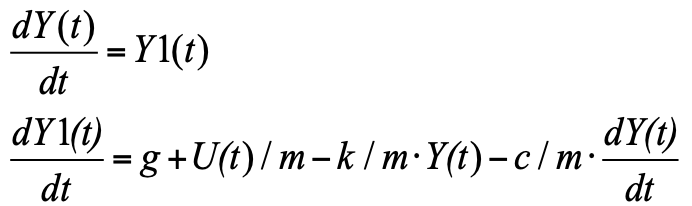
يمكن ببساطة كتابة هذه المعادلة في المربع "لغة البرمجة" والحصول على النموذج (انظر الشكل 3):
الشكل 3. نموذج المثبط في لغة البرمجة.كمدخلات ، نستخدم قيمة القوة U ، والإخراج من الكتلة هو الإزاحة Y ، ويتم إعطاء الموضع الأولي بالصيغة 3. ويتم تعيين جميع المتغيرات كإشارات عالمية للمشروع:
الشكل 4. متغيرات المشروع العالمي.يمكن أيضًا إنشاء نموذج المثبط في شكل هيكل ، في الشكل 5 ، والذي يوضح نموذج المثبط الموازي الذي تم إنشاؤه من كتل قياسية ، حيث تكون الشرط الأولي في وحدة التكامل عند الخرج (انظر الشكل 6) ، ويتم إدخال المعاملات في المُعلن (انظر الشكل. 7)
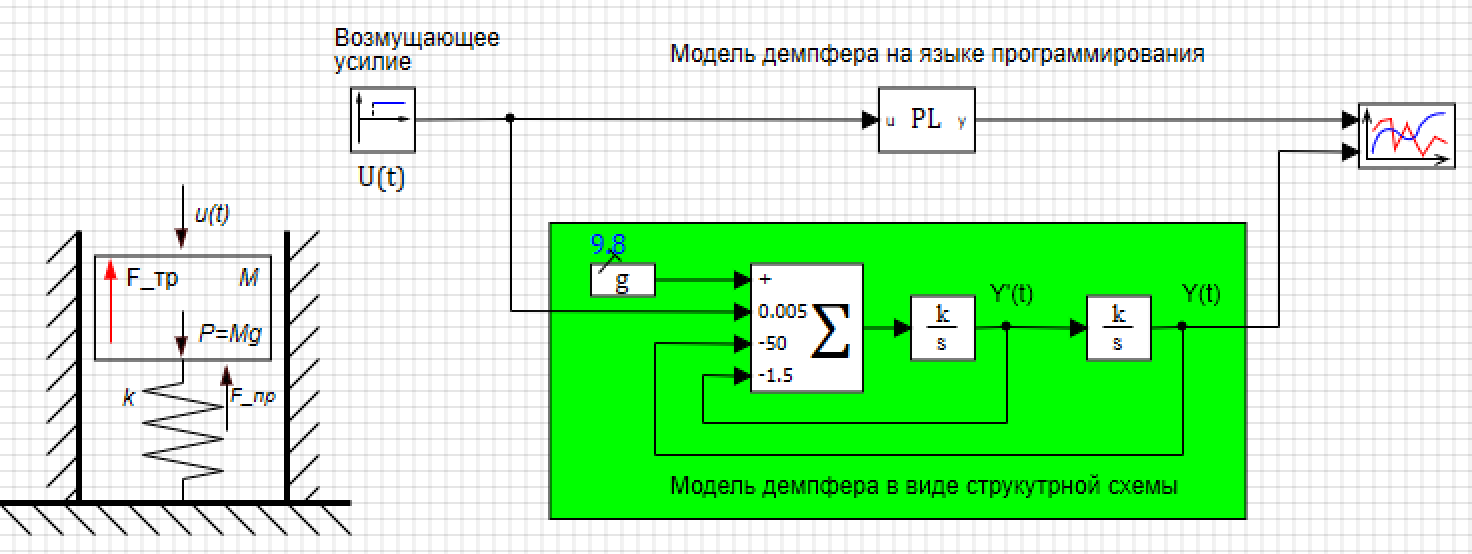الشكل 5. المثبط في لغة البرمجة وفي شكل الرسم البياني الهيكلي.
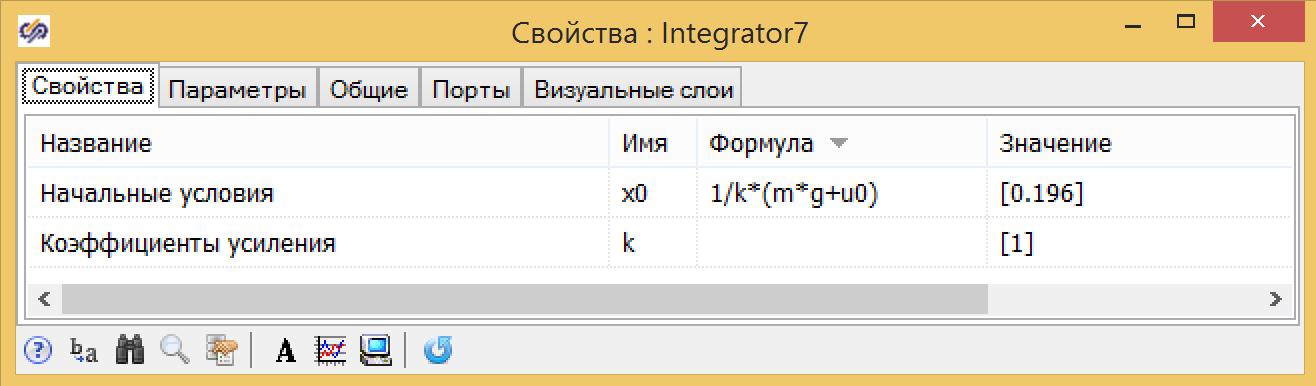الشكل 6. الملكية المتكاملة مع الظروف الأولية.
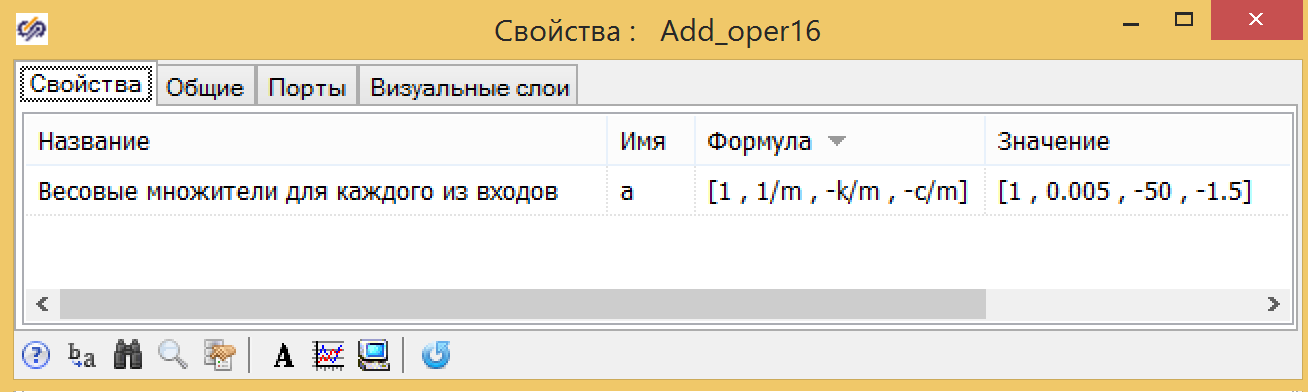الشكل 7. خصائص الأفعى مع المعاملات.وضعنا التأثير المضطرب لمدة 10 ثوانٍ ، ونغير القوة المؤثرة من 0 إلى 30 ، في قفزة ، ونتأكد من أن النموذجين يظهران نفس النتيجة (انظر الشكل 8).
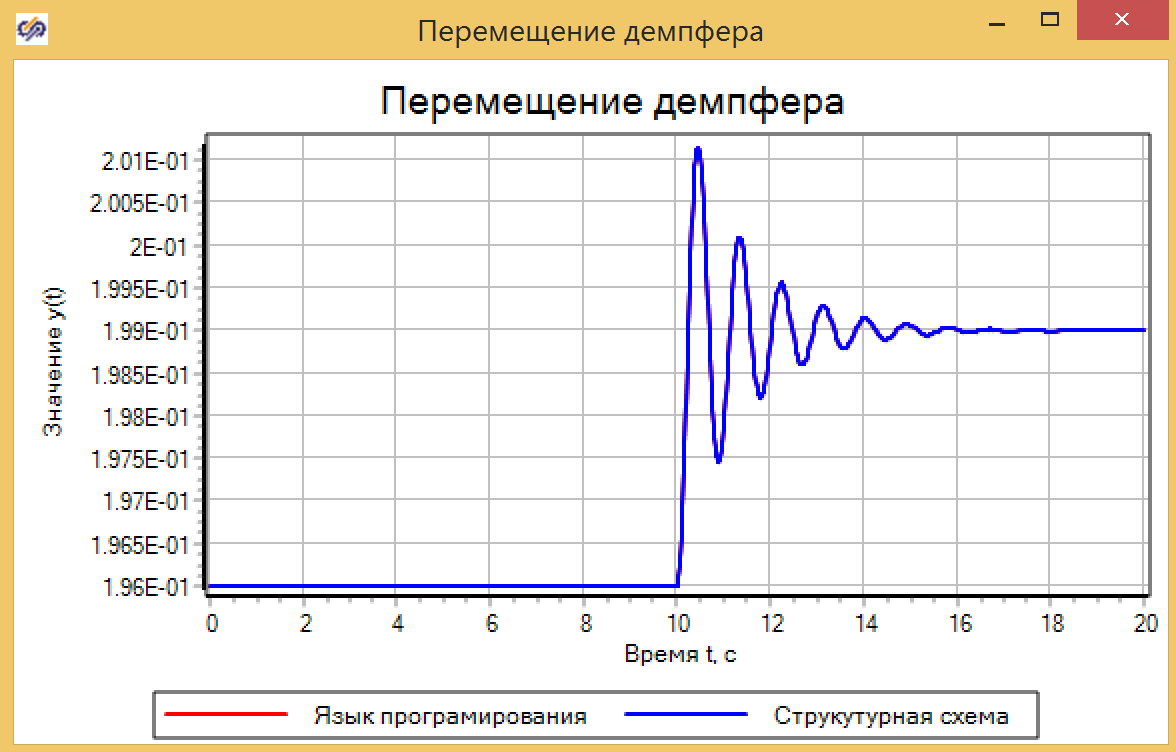الشكل 8. تحريك المثبط.دعنا نتحقق من النموذج في شكل وظيفة نقل في شكل عام وفي شكل رابط متذبذب ، وهذا النظام هو. للقيام بذلك ، نقوم بتجميع الدائرة ، كما هو مبين في الشكل 9.
الشكل 9. نموذجين المثبط في شكل وظائف النقل.يجب أن يؤخذ في الاعتبار أننا قمنا بتجميع الرسم البياني في الانحرافات ، وبالتالي ، للحصول على القيمة المطلقة ، من الضروري إضافة ثابت - الموضع الأولي للمكبس.
بالنسبة لوظيفة النقل (الصيغة 7) ، نستخدم نفس الثوابت والتعبيرات العالمية التي تم الحصول عليها سابقًا في
k 1 و T 1 و T 2 (انظر الشكل 10).
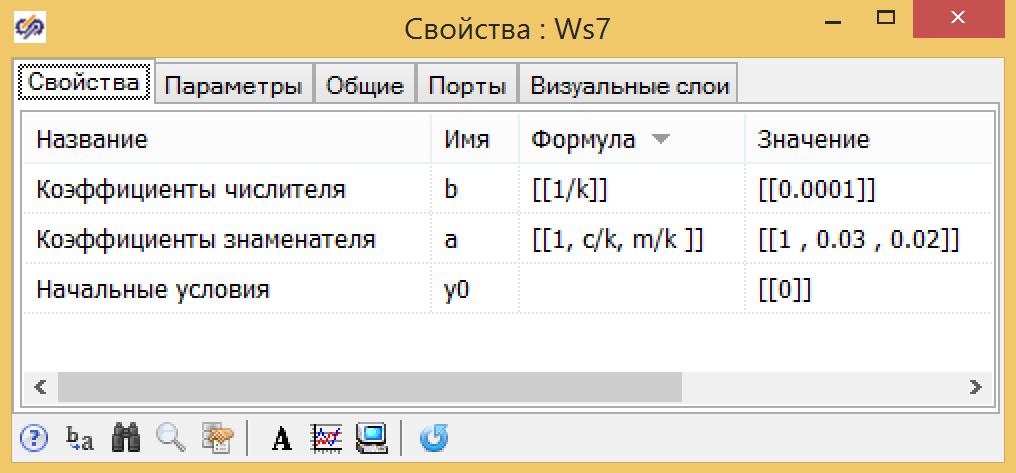الشكل 10. معلمات وظيفة نقل النموذج العام.بالنسبة لمعايير الارتباط الذبذبي ، فإن الصيغ أكثر تعقيدًا قليلاً ، ولكن يمكن التعبير عنها جميعًا من حيث المعلمات العالمية: كتلة المكبس ، معامل السحب الربيعي - k ، معامل الاحتكاك (انظر الشكل 11).
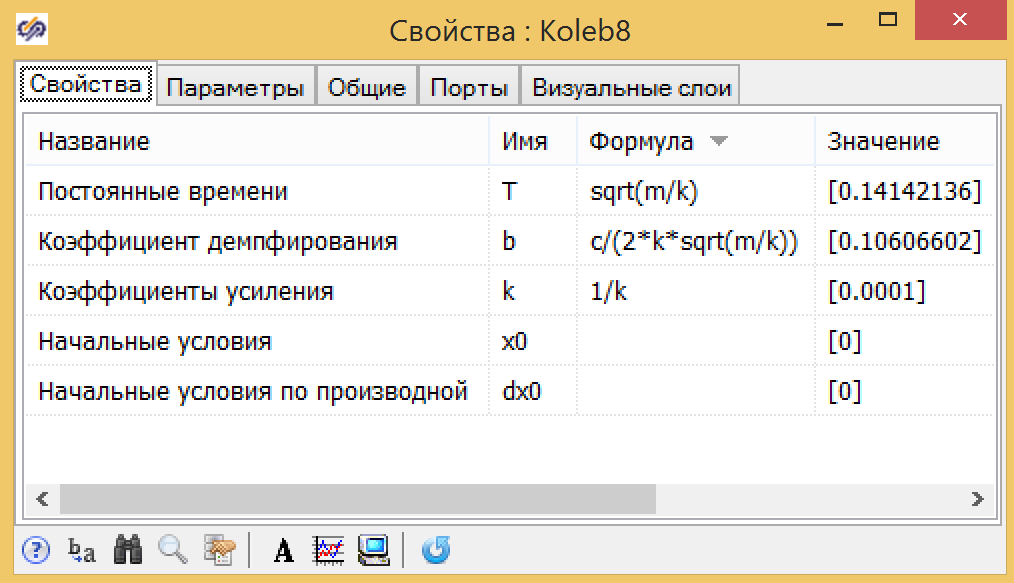الشكل 11. معلمات الارتباط الاهتزاز.تظهر الرسوم البيانية الانتقالية (انظر الشكل 12) أن TAU السحر يعمل حقا. تعطي وظيفة النقل نفس النتائج تمامًا كنموذج قائم على معادلات الفيزياء.
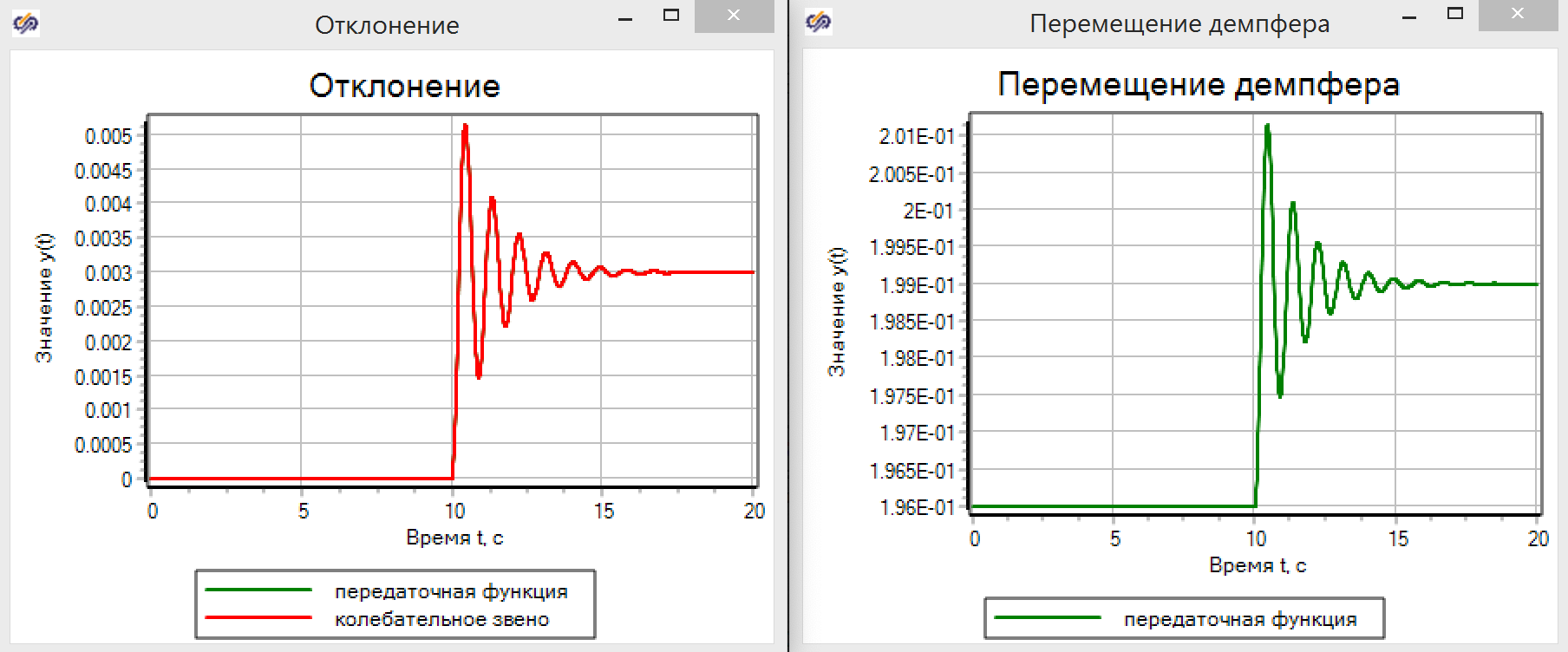الشكل 12. نقل المثبط في نماذج TAU.تخيل أننا لا نملك نموذجًا ، ونستخدم وحدة تحديد الهوية وفقًا للبيانات التي تم الحصول عليها من التجربة. هناك تقنية كاملة من وظائف تحليل البيانات ونقلها ، ولكن كجزء من المقالة وكمثال على ذلك ، سنقوم بتوصيل لبنة بناء وظيفة النقل بالنموذج في شكل لغة برمجة ، كما هو مبين في الشكل 13. ونعتقد أن لدينا نموذج "الصندوق الأسود" ، و نحن لا نعرف ما هو في الداخل.
الشكل 13. مخطط اتصال المعرف الزائف.نتيجة لتحليل الكتلة الخاصة بنا بلغة برمجة ، حصلنا على وظيفة نقل ، والتي لا تختلف عملياً عن الوظيفة الأولية ، المستمدة من المعادلات (انظر الشكل 14.). قارن مع الشكل 10. هنا هو زر سحري!
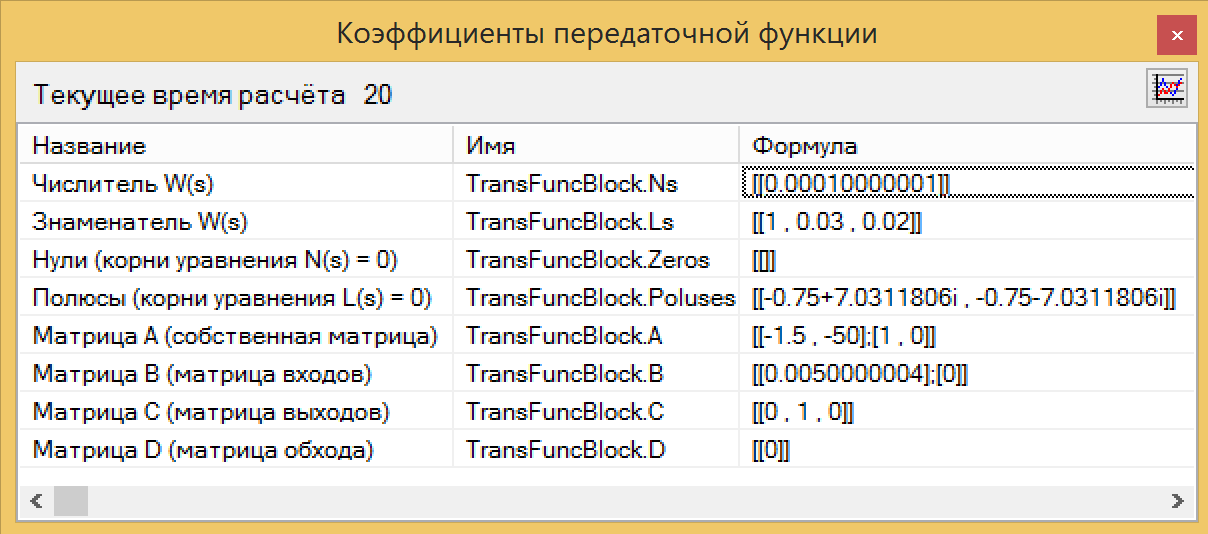الشكل 14. تحديد وظيفة النقل.يمكن نسخ قيم البسط والمقام مباشرة من كتلة التعريف ، ولصقها في كتلة وظيفة النقل والتأكد من مطابقة الرسوم البيانية. أعمال السحر تاو.
دورة فضح السحر
فلماذا لا يمكنك دائمًا استخدام "تعريف النظام" لعملية تصميم نموذجية المنحى عندما يكون كل شيء سحريًا؟
لفهم عيوب النماذج التي تم الحصول عليها عن طريق تحديد المربع الأسود لتعريف النظام ، حاول الإجابة على سؤال بسيط: ما هو انحراف المثبط عند زيادة كتلة المكبس بنسبة 30٪؟
ثم اتضح أن ليس كل الزبادي مفيدون بنفس القدر.
إذا كانت لديك معادلات صادقة ، يمكنك ببساطة تغيير كتلة الحمل في المتغيرات العامة للمشروع والحصول على عملية انتقال جديدة ، ووظيفة نقل جديدة.
في حالة ، بدلاً من المعادلات الصادقة للفيزياء ، لديك بالفعل وظيفة نقل تم إنشاؤها من نتائج التجربة ، تحتاج إلى تشغيل مرة أخرى وإجراء التجربة لفهم كيف سيؤثر التغيير في الكتلة على سلوك النموذج. كما يقولون ، والرأس السيئ لا يعطي الراحة في الساقين.
الاستنتاجات:
- إن الجلوس والتفكير في معادلات الفيزياء دائمًا ما يكون أكثر فائدة وأرخص من التجربة.
- يعتبر النموذج المستمد من المعادلات المادية للعمليات أكثر ذوقًا وأكثر فائدة من وظائف النقل.
- يجب أن توضح التجربة المعاملات غير المعروفة أو يصعب قياس المعلمات.
- تعلم الفيزياء وسوف تكون سعيدا!
يمكن أخذ الملف مع نموذج المثبط للتجارب
هنا ...