اسمي فياتشيسلاف ، أنا عالم رياضيات مزمن ولعدة سنوات لم أستخدم دورات عند العمل مع المصفوفات ...

بالضبط منذ أن اكتشفت عمليات المتجهات في NumPy. أرغب في تعريفك بوظائف NumPy التي أستخدمها غالبًا لمعالجة صفائف البيانات والصور. في نهاية المقالة ، سأبين كيف يمكنك استخدام مجموعة أدوات NumPy لإقحام الصور بدون تكرار (= سريع جدًا).

لا تنسى

import numpy as np 

ودعنا نذهب!


محتوى

ما هو شرير؟
إنشاء صفيف
الوصول إلى العناصر والشرائح
شكل الصفيف وتغييره
إعادة ترتيب المحور والتنقل
صفيف الانضمام
استنساخ البيانات
العمليات الرياضية على عناصر الصفيف
مصفوفة الضرب
تجميع
بدلا من الاستنتاج - مثال

ما هو شرير؟

هذه مكتبة مفتوحة المصدر تم فصلها مرة واحدة عن مشروع SciPy. NumPy هو سليل Numeric و NumArray. يستند NumPy إلى مكتبة LAPAC ، التي تتم كتابتها في فورتران. بديل غير بيثون لـ NumPy هو Matlab.

نظرًا لحقيقة أن NumPy يستند إلى فورتران ، فهي مكتبة سريعة. ونظرًا لحقيقة أنه يدعم عمليات مكافحة ناقلات الصفائف متعددة الأبعاد ، فهو مريح للغاية.

بالإضافة إلى الإصدار الأساسي (المصفوفات متعددة الأبعاد في الإصدار الأساسي) ، يتضمن NumPy مجموعة من الحزم لحل المهام المتخصصة ، على سبيل المثال:

• numpy.linalg - تنفذ عمليات الجبر الخطي (الضرب البسيط للناقلات والمصفوفات موجود في الإصدار الأساسي) ؛
• numpy.random - تنفذ وظائف للعمل مع المتغيرات العشوائية ؛
• numpy.fft - تنفذ تحويل فورييه المباشر والعكسي.

لذا ، أقترح أن تنظر بالتفصيل في بعض ميزات NumPy وأمثلة لاستخدامها ، والتي ستكون كافية لك لفهم مدى قوة هذه الأداة!

<أعلى>

إنشاء صفيف

هناك عدة طرق لإنشاء صفيف:

1. تحويل القائمة إلى مجموعة:
   
   

    A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]]) 

2. انسخ الصفيف (نسخة ونسخة عميقة مطلوبة !!!):
   
   

    B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]]) 

3. إنشاء صفيف أو صفيف واحد بحجم معين:
   
   

    A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]]) 

   
   

    B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]]) 

   
   أو خذ أبعاد مجموعة موجودة:
   
   

    A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]]) 

   
   

    A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]]) 

   
   
4. عند إنشاء صفيف مربع ثنائي الأبعاد ، يمكنك جعله مصفوفة قطرية لوحدة:
   
   

    A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]]) 

5. بناء مجموعة من الأرقام من (بما في ذلك) إلى (لا تشمل) مع الخطوة الخطوة:
   
   

    From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5]) 

   
   بشكل افتراضي ، من = 0 ، الخطوة = 1 ، لذلك يتم تفسير المتغير مع معلمة واحدة إلى:
   
   

    A = np.arange(5) A Out: array([0, 1, 2, 3, 4]) 

   
   أو مع اثنين - مثل من والى:
   
   

    A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14]) 

لاحظ أنه في الطريقة رقم 3 ، تم تمرير أبعاد المصفوفة كمعلمة واحدة (مجموعة من الأحجام). المعلمة الثانية في الأساليب رقم 3 ورقم 4 ، يمكنك تحديد النوع المطلوب من عناصر مجموعة:

 A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]]) 

 B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]]) 

باستخدام طريقة astype ، يمكنك إرسال الصفيف إلى نوع مختلف. يشار إلى النوع المطلوب كمعلمة:

 A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32') 

يمكن العثور على جميع الأنواع المتاحة في قاموس sctypes:

 np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]} 

<أعلى>

الوصول إلى العناصر والشرائح

يتم الوصول إلى عناصر المصفوفة بواسطة مؤشرات عدد صحيح ، يبدأ العد التنازلي من 0:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5 

إذا كنت تتخيل صفيفًا متعدد الأبعاد كنظام للصفائف أحادية البعد المتداخلة (صفيف خطي ، يمكن أن تكون عناصره صفائف خطية) ، يصبح من الواضح أنه يمكنك الوصول إلى المصفوفات الفرعية باستخدام مجموعة غير كاملة من الفهارس:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6]) 

بالنظر إلى هذا النموذج ، يمكننا إعادة كتابة مثال الوصول إلى عنصر واحد:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5 

عند استخدام مجموعة غير كاملة من المؤشرات ، يتم استبدال المؤشرات المفقودة ضمنيًا بقائمة بجميع المؤشرات الممكنة على طول المحور المقابل. يمكنك القيام بذلك بشكل صريح عن طريق تعيين ":". يمكن إعادة كتابة المثال السابق مع فهرس واحد كما يلي:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6]) 

يمكنك تخطي فهرس على أي محور أو محاور ؛ إذا كان المحور متبوعًا بمحاور مع الفهرسة ، فحينئذٍ يجب: ":":

 A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5]) 

يمكن أن تأخذ الفهارس قيم عدد صحيح سالبة. في هذه الحالة ، يكون العدد من نهاية الصفيف:

 A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4 

لا يمكنك استخدام فهارس واحدة ، لكن قوائم الفهارس على طول كل محور:

 A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4]) 

أو يتراوح الفهرس في شكل "من: إلى: الخطوة". ويسمى هذا التصميم شريحة. يتم تحديد جميع العناصر وفقًا لقائمة المؤشرات التي تبدأ من الفهرس من شاملة ، إلى الفهرس إلى لا بما في ذلك خطوة الخطوة:

 A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2]) 

تحتوي خطوة الفهرس على قيمة افتراضية قدرها 1 ويمكن تخطيها:

 A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3]) 

تحتوي القيم من و إلى أيضًا على القيم الافتراضية: 0 وحجم الصفيف على طول محور الفهرس ، على التوالي:

 A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3]) 

 A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4]) 

إذا كنت تريد استخدام "من و إلى" افتراضيًا (جميع المؤشرات الموجودة في هذا المحور) والخطوة مختلفة عن 1 ، فأنت بحاجة إلى استخدام اثنين من أزواج من نقطتين حتى يتسنى للمترجم تحديد معلمة واحدة على أنها "خطوة". تعمل التعليمة البرمجية التالية على "توسيع" الصفيف على طول المحور الثاني ، ولكن لا يتغير على طول الأول:

 A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]] 

الآن دعونا نفعل ذلك

 print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]] 

كما ترون ، من خلال B قمنا بتغيير البيانات في A. لهذا السبب من المهم استخدام النسخ في مهام حقيقية. يجب أن يبدو المثال أعلاه كما يلي:

 A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]] 

يوفر NumPy أيضًا القدرة على الوصول إلى عناصر صفيف متعددة من خلال مجموعة فهرس منطقية. يجب أن يتطابق صفيف الفهرس مع شكل المفهرسة.

 A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6]) 

كما ترون ، فإن مثل هذا البناء يعرض صفيفًا مسطحًا يتكون من عناصر من الصفيف المفهرسة التي تتوافق مع الفهارس الحقيقية. ومع ذلك ، إذا استخدمنا هذا الوصول إلى عناصر المصفوفة لتغيير قيمها ، فسيتم الحفاظ على شكل المصفوفة:

 A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]] 

العمليات المنطقية يتم تعريف logical_and و logical_or و logical_not على فهرسة صفيفات منطقية وتنفيذ عمليات منطقية AND و OR و NOT عنصريًا:

 A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]] 

logical_and و logical_or يأخذان عاملين ، logical_not يأخذان واحدة. يمكنك استخدام عوامل التشغيل & ، | و ~ لتنفيذ AND و OR و NOT ، على التوالي ، مع أي عدد من المعاملات:

 A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]] 

وهو ما يعادل استخدام I1 فقط.

من الممكن الحصول على صفيف منطقي للفهرسة يتوافق في صفيف مع مجموعة من القيم عن طريق كتابة شرط منطقي مع اسم الصفيف باعتباره معامل. سيتم حساب القيمة المنطقية للفهرس كحقيقة التعبير لعنصر الصفيف المقابل.

ابحث عن صفيف فهرسة لعناصر I أكبر من 3 وعناصر ذات قيم أقل من 2 وأكثر من 4 - سيتم إعادة تعيينها إلى صفر:

 A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]] 

<أعلى>

شكل الصفيف وتغييره

يمكن تمثيل مصفوفة متعددة الأبعاد كصفيف أحادي البعد للطول الأقصى ، مقطوعًا إلى أجزاء بطول المحور الأخير للغاية ووضع في طبقات بطول المحاور ، بدءًا من الأخير.

من أجل الوضوح ، فكر في مثال:

 A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]] 

في هذا المثال ، قمنا بتكوين صفيفتين جديدتين من صفيف أحادي البعد بطول 24 عنصرًا. Array B ، حجم 4 في 6. إذا نظرت إلى ترتيب القيم ، يمكنك أن ترى أنه على طول البعد الثاني توجد سلاسل من القيم المتتالية.

في الصفيف C ، 4 × 3 في 2 ، تعمل القيم المستمرة على طول المحور الأخير. على طول المحور الثاني عبارة عن كتل متسلسلة ، والتي قد ينتج عن الجمع بينها صف على طول المحور الثاني للصفيف B.

ونظرًا لأننا لم نقوم بعمل نسخ ، يصبح من الواضح أن هذه أشكال مختلفة من تمثيل صفيف البيانات نفسه. لذلك ، يمكنك بسهولة وبسرعة تغيير شكل الصفيف دون تغيير البيانات نفسها.

لاكتشاف أبعاد المصفوفة (عدد المحاور) ، يمكنك استخدام حقل ndim (العدد) ، ومعرفة الحجم على طول كل شكل محور (tuple). يمكن أيضًا التعرف على البعد بطول الشكل. لمعرفة إجمالي عدد العناصر في صفيف ، يمكنك استخدام قيمة الحجم:

 A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24 

لاحظ أن ndim والشكل سمات ، وليس أساليب!

لرؤية الصفيف أحادي البعد ، يمكنك استخدام وظيفة ravel:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6]) 

لتغيير حجمها على طول المحاور أو البعد ، استخدم طريقة إعادة التشكيل:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]]) 

من المهم الحفاظ على عدد العناصر. خلاف ذلك ، سوف يحدث خطأ:

 A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3) 

بالنظر إلى أن عدد العناصر ثابت ، يمكن حساب الحجم على طول أي محور عند إعادة التشكيل من قيم الطول على محاور أخرى. يمكن تعيين الحجم على طول محور واحد -1 ثم يتم حسابه تلقائيًا:

 A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2) 

يمكنك استخدام إعادة التشكيل بدلاً من ravel:

 A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,) 

النظر في التطبيق العملي لبعض الميزات لمعالجة الصور. ككائن للبحث ، سوف نستخدم صورة:



دعونا نحاول تنزيله وتصوره باستخدام Python. لهذا نحتاج OpenCV و Matplotlib:

 import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show() 

ستكون النتيجة مثل هذا:



انتبه إلى شريط التنزيل:

 I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3) 

يعمل OpenCV مع الصور بتنسيق BGR ، ونحن معتادون على RGB. نقوم بتغيير ترتيب البايت على طول محور اللون دون الوصول إلى وظائف OpenCV باستخدام البنية
"[:،:، :: :: 1]".

قم بتقليل الصورة مرتين في كل محور. صورتنا لها أبعاد متساوية على طول المحاور ، على التوالي ، يمكن تقليلها دون الاستيفاء:

 I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show() 

عند تغيير شكل المصفوفة ، حصلنا على محورين جديدين ، قيمتين في كل منهما ، وهي تتوافق مع إطارات مكونة من صفوف وأعمدة فردية وغريبة من الصورة الأصلية.
جودة رديئة هي نتيجة لاستخدام Matplotlib ، لأنه يمكنك أن ترى الأبعاد المحورية. في الواقع ، فإن جودة الصورة المصغرة هي:



<أعلى>

إعادة ترتيب المحور والتنقل

بالإضافة إلى تغيير شكل المصفوفة بنفس ترتيب وحدات البيانات ، من الضروري غالبًا تغيير ترتيب المحاور ، مما يستلزم بطبيعة الحال التقليب في كتل البيانات.

مثال على هذا التحول هو تبديل المصفوفة: تبادل الصفوف والأعمدة.

 A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6] 

في هذا المثال ، تم استخدام بنية AT لتغيير المصفوفة A. يقوم عامل النقل بتبديل ترتيب المحور. النظر في مثال آخر مع ثلاثة محاور:

 C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]] 

يحتوي هذا الإدخال القصير على نظير أطول: np.transpose (A). هذه أداة أكثر تنوعًا لاستبدال ترتيب المحور. تتيح لك المعلمة الثانية تحديد مجموعة من أرقام محور الصفيف المصدر ، والتي تحدد ترتيب موضعها في الصفيف الناتج.

على سبيل المثال ، أعد ترتيب أول محورين من الصورة. يجب أن تقلب الصورة مع ترك محور اللون بدون تغيير:

 I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show() 

في هذا المثال ، يمكن استخدام أداة swapaxes أخرى. يبدل هذا الأسلوب المحورين المحددين في المعلمات. المثال أعلاه يمكن تنفيذه مثل هذا:

 I_ = np.swapaxes(I, 0, 1) 

<أعلى>

صفيف الانضمام

يجب أن تحتوي الصفائف المدمجة على نفس عدد المحاور. يمكن دمج الصفائف بتكوين محور جديد ، أو على طول محور موجود.

للاندماج مع تكوين محور جديد ، يجب أن يكون للصفائف الأصلية نفس الأبعاد على طول جميع المحاور:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]]) 

كما ترى من المثال ، أصبحت صفائف المعامِلات صفائف فرعية للكائن الجديد ومُصطفة على طول المحور الجديد ، وهو الأول من حيث الترتيب.

لدمج الصفائف على محور موجود ، يجب أن يكون لها نفس الحجم على جميع المحاور باستثناء المحور المحدد للانضمام ، ويمكن أن يكون لها أحجام تعسفية على طوله:

 A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]]) 

للجمع بين المحور الأول أو الثاني ، يمكنك استخدام طريقتي vstack و hstack ، على التوالي. نعرض هذا مع مثال على الصور. يجمع vstack بين الصور ذات العرض نفسه في الارتفاع ، بينما يجمع hsstack بين الصور ذات الارتفاع في عرض واحد:

 I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show() 

يرجى ملاحظة أنه في جميع أمثلة هذا القسم ، يتم تمرير الصفائف المرتبطة بواسطة معلمة واحدة (tuple). يمكن أن يكون عدد المعاملات ، ولكن ليس بالضرورة 2.

انتبه أيضًا إلى ما يحدث للذاكرة عند الجمع بين المصفوفات:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]] 

منذ إنشاء كائن جديد ، يتم نسخ البيانات الموجودة به من الصفائف الأصلية ، لذلك لا تؤثر التغييرات في البيانات الجديدة على الأصل.

<أعلى>

استنساخ البيانات

سيقوم عامل التشغيل np.repeat (A، n) بإرجاع صفيف أحادي البعد مع عناصر من الصفيف A ، سيتم تكرار كل منها n مرة.

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8] 

بعد هذا التحويل ، يمكنك إعادة إنشاء هندسة المصفوفة وجمع البيانات المكررة في محور واحد:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]] 

يختلف هذا الخيار عن دمج المصفوفة مع مشغل المكدس نفسه فقط في موضع المحور الذي توجد عليه نفس البيانات. في المثال أعلاه ، هذا هو المحور الأخير ، إذا استخدمت المكدس - الأول:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]] 

بغض النظر عن كيفية استنساخ البيانات ، فإن الخطوة التالية هي تحريك المحور الذي تقف عليه القيم نفسها في أي موضع مع نظام المحور:

 A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] 

إذا كنا نريد "تمديد" أي محور باستخدام تكرار العناصر ، فيجب وضع المحور بنفس القيم بعد التمديد (استخدام تبديل) ، ثم دمج هذين المحورين (باستخدام إعادة التشكيل). فكر في مثال على مد صورة على طول المحور العمودي عن طريق تكرار الصفوف:

 I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1] #    I1 = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1)[:, 0, :, 0] #      I2 = np.repeat(I1, 2) #   I3 = I2.reshape(I1.shape[0], I1.shape[1], I1.shape[2], -1) I4 = np.transpose(I3, (0, 3, 1, 2)) #    I5 = I4.reshape(-1, I1.shape[1], I1.shape[2]) #   print('I0', I0.shape) print('I1', I1.shape) print('I2', I2.shape) print('I3', I3.shape) print('I4', I4.shape) print('I5', I5.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I5) plt.show() Out: I0 (1280, 1920, 3) I1 (640, 960, 3) I2 (3686400,) I3 (640, 960, 3, 2) I4 (640, 2, 960, 3) I5 (1280, 960, 3) 

<أعلى>

العمليات الرياضية على عناصر الصفيف

إذا كانت A و B صفيفين من نفس الحجم ، فيمكن إضافتهما وضربهما وطرحهما وتقسيمهما ورفعهما إلى السلطة. يتم تنفيذ هذه العمليات من حيث العنصر ، وسوف يتزامن الصفيف الناتج في الهندسة مع المصفوفات الأصلية ، وسيكون كل عنصر نتيجة العملية المقابلة على زوج من العناصر من المصفوفات الأصلية:

 A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]] 

يمكنك إجراء أي عملية من أعلاه على المصفوفة والرقم. في هذه الحالة ، سيتم تنفيذ العملية أيضًا على كل عنصر من عناصر المصفوفة:

 A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]] 

بالنظر إلى أن المصفوفة متعددة الأبعاد يمكن اعتبارها مصفوفة مسطحة (المحور الأول) ، وعناصرها صفائف (محاور أخرى) ، من الممكن إجراء العمليات المدروسة على المصفوفات A و B في الحالة عندما تتزامن الهندسة B مع هندسة المصفوفات الفرعية A مع قيمة ثابتة على طول المحور الأول . بمعنى آخر ، مع نفس عدد المحاور والأحجام A [i] و B. في هذه الحالة ، سيكون كل من الصفيفين A [i] و B معاملات للعمليات المحددة في المصفوفات.

 A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]] 

في هذا المثال ، يتعرض الصفيف B للعمل مع كل صف من الصفيف أ. إذا كنت بحاجة إلى ضرب / تقسيم / إضافة / طرح / رفع درجة المصفوفات الفرعية على طول محور آخر ، فأنت بحاجة إلى استخدام تبديل لوضع المحور المطلوب في مكانه الأول ، ثم إعادته إلى مكانه. النظر في المثال أعلاه ، ولكن مع الضرب من قبل المتجه B لأعمدة الصفيف A:

 A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]] 

بالنسبة للوظائف الأكثر تعقيدًا (على سبيل المثال ، المثلثية ، الأس ، اللوغاريتم ، التحويل بين الدرجات والراديان ، المعامل ، الجذر التربيعي ، إلخ) ، NumPy لديه تطبيق. النظر في مثال الأسي واللوغاريتم:

 A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] 

يمكن العثور على قائمة كاملة بالعمليات الرياضية في NumPy هنا .

<أعلى>

مصفوفة الضرب

يتم تنفيذ العملية المذكورة أعلاه لمنتج الصفائف بشكل أولي. وإذا كنت بحاجة إلى إجراء عمليات وفقًا لقواعد الجبر الخطي على المصفوفات كما في التينورات ، فيمكنك استخدام طريقة النقطة (A ، B). حسب نوع المعامل ، ستقوم الوظيفة:

• إذا كانت الوسيطات عدديًا (أرقام) ، فسيتم إجراء الضرب ؛
• إذا كانت الوسيطات عبارة عن متجه (صفيف أحادي البعد) وقيم ، فسيتم ضرب المصفوفة برقم ؛
• إذا كانت الوسيطات متجهة ، فسيتم إجراء الضرب العددي (مجموع المنتجات الحكيمة) ؛
• إذا كانت الحجج متوترة (صفيف متعدد الأبعاد) وقيمية ، فسيتم ضرب المتجه برقم ؛
• إذا كانت حجج التينسور ، فسيتم تنفيذ ناتج التنسورات على طول المحور الأخير للوسيطة الأولى وما قبل الأخيرة ؛
• إذا كانت الحجج عبارة عن مصفوفات ، فسيتم تنفيذ منتج المصفوفات (هذه حالة خاصة لمنتج التنسورات) ؛
• إذا كانت الوسائط عبارة عن مصفوفة وناقلات ، فسيتم تنفيذ منتج المصفوفة والناقل (وهذه أيضًا حالة خاصة لمنتج التنسورات).

لتنفيذ العمليات ، يجب أن تتزامن الأحجام المقابلة: بالنسبة للناقلات الطولية ، بالنسبة إلى التنسورات ، فإن الأطوال على طول المحاور التي سيتم من خلالها تجميع المنتجات ذات العناصر.

النظر في أمثلة مع العددية والمتجهات:

 #  A = 2 B = 3 print(np.dot(A, B), '\n') #    A = np.array([2., 3., 4.]) B = 3 print(np.dot(A, B), '\n') #  A = np.array([2., 3., 4.]) B = np.array([-2., 1., -1.]) print(np.dot(A, B), '\n') #    A = np.array([[2., 3., 4.], [5., 6., 7.]]) B = 2 print(np.dot(A, B), '\n') Out: 6 [ 6. 9. 12.] -5.0 [[ 4. 6. 8.] [10. 12. 14.]] 

مع التنسورات ، سننظر فقط في كيفية تغير هندسة الصفيف الناتج في الحجم:

 #  ( 2)   ( 1) A = np.ones((5, 6)) B = np.ones(6) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.dot(A, B).shape, '\n\n') #  ( 2) A = np.ones((5, 6)) B = np.ones((6, 7)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.dot(A, B).shape, '\n\n') #   A = np.ones((5, 6, 7, 8)) B = np.ones((1, 2, 3, 8, 4)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.dot(A, B).shape, '\n\n') Out: A: (5, 6) B: (6,) result: (5,) A: (5, 6) B: (6, 7) result: (5, 7) A: (5, 6, 7, 8) B: (1, 2, 3, 8, 4) result: (5, 6, 7, 1, 2, 3, 4) 

لتنفيذ منتج tensor باستخدام محاور أخرى ، بدلاً من تلك المحددة في نقطة ، يمكنك استخدام tensordot مع محور صريح:

 A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8) 

لقد أوضحنا صراحة أننا نستخدم المحور الثالث للصفيف الأول والثاني - الثاني (يجب أن تتطابق الأحجام على طول هذه المحاور).

<أعلى>

تجميع

أدوات التجميع هي طرق NumPy تسمح لك باستبدال البيانات بخصائص متكاملة على طول بعض المحاور. على سبيل المثال ، يمكنك حساب متوسط ​​القيمة أو الحد الأقصى أو الحد الأدنى أو التباين أو بعض الخصائص الأخرى على طول أي محور أو محاور وتشكيل مجموعة جديدة من هذه البيانات. سيحتوي شكل المصفوفة الجديدة على جميع محاور المصفوفة الأصلية ، باستثناء المحاور التي تم حساب المجمع فيها.

على سبيل المثال ، سنشكل مجموعة ذات قيم عشوائية. ثم نجد الحد الأدنى والحد الأقصى والقيمة المتوسطة في أعمدةها:

 A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] 

في هذا الاستخدام، يعني و متوسط مرادفا نظرة. ولكن هذه الوظائف لديها مجموعة مختلفة من المعلمات الإضافية. هناك احتمالات مختلفة لإخفاء ووزن المتوسط ​​للبيانات.

يمكنك حساب الخصائص المتكاملة في عدة محاور:

 A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.] 

في هذا المثال ، يُعتبر المبلغ المميز المتكامل الآخر - المجموع.

قائمة التجميعات تبدو مثل هذا:

• sum: sum and nansum - متغير يعمل بشكل صحيح مع nan ؛
• العمل: همز و nanprod.
• المتوسط ​​والتوقع: متوسط ​​ومتوسط ​​(nanmean) ، لا يوجد متوسط ​​nana ؛
• متوسط: متوسط ​​و nanmedian.
• المئين: المئين و nanpercentile.
• الاختلاف: فار و nanvar.
• الانحراف المعياري (الجذر التربيعي للاختلاف): الأمراض المنقولة جنسيا و nanstd ؛
• : min nanmin;
• : max nanmax;
• , : argmin nanargmin;
• , : argmax nanargmax.

في حالة استخدام argmin و argmax (على التوالي ، كل من nanargmin و nanargmax) ، يجب عليك تحديد محور واحد يتم من خلاله النظر في الخاصية المميزة.

إذا لم تحدد محورًا ، فسيتم اعتبار جميع الخصائص التي تم النظر فيها افتراضيًا في الصفيف. في هذه الحالة ، يعمل كل من argmin و argmax بشكل صحيح وإيجاد فهرس الحد الأقصى أو الحد الأدنى للعنصر ، كما لو أن جميع البيانات الموجودة في المصفوفة قد امتدت على طول المحور نفسه باستخدام الأمر ravel ().

تجدر الإشارة أيضًا إلى أن أساليب التجميع لا يتم تعريفها فقط كطرق لوحدة NumPy ، ولكن أيضًا للصفائف نفسها: يكون الإدخال np.aggregator (A ، axes) مكافئًا للإدخال A.aggregator (المحاور) ، حيث يعني المجمّع إحدى الوظائف المذكورة أعلاه ، وبواسطة محاور - مؤشرات المحور.

 A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.] 

<الأعلى>

بدلا من الاستنتاج - مثال

دعونا نبني خوارزمية لتصفية الصور الخطية منخفضة المرور.

للبدء ، قم بتحميل صورة صاخبة.



النظر في جزء من الصورة لرؤية الضوضاء:



سنقوم بتصفية الصورة باستخدام مرشح غاوسي. ولكن بدلاً من القيام بالإلتفاف مباشرة (مع التكرار) ، فإننا نطبق المتوسط ​​المرجح لشرائح الصورة التي تحولت نسبة إلى بعضها البعض:

 def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J 

نطبق هذه الوظيفة على صورتنا مرة ومرتين وثلاث مرات:

 I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3) 

نحصل على النتائج التالية:





مع استخدام واحد للمرشح ؛





مع ضعف.





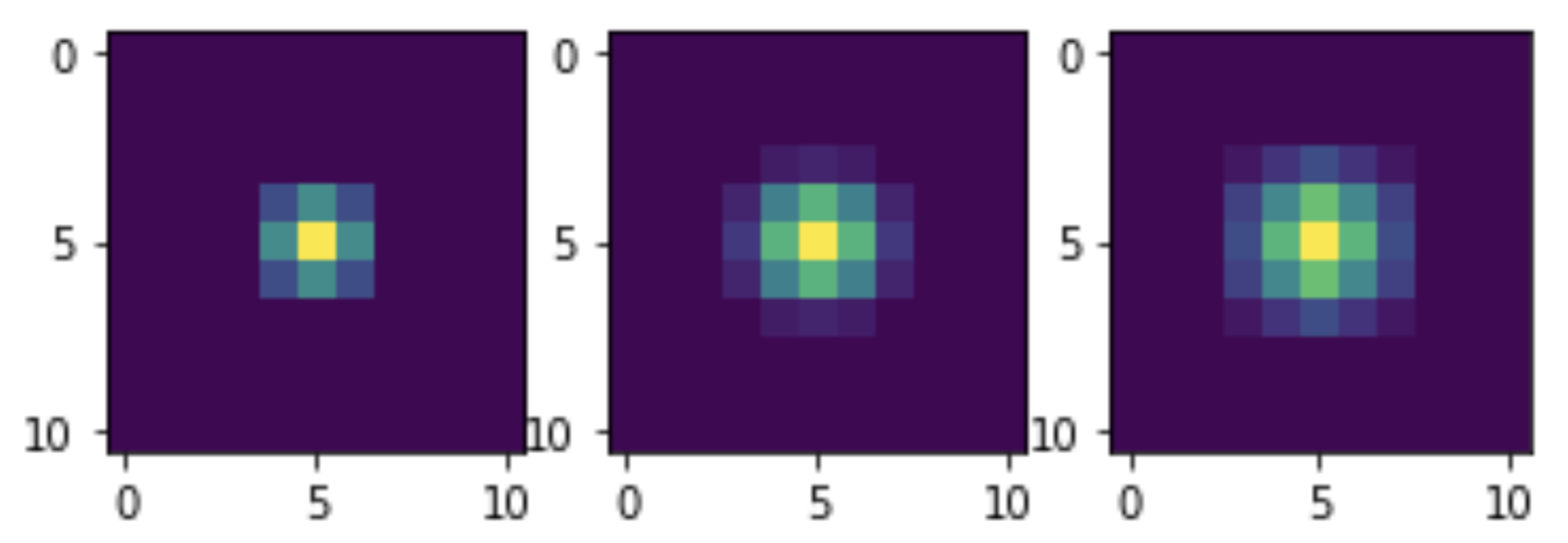
في ثلاث مرات.

يمكن ملاحظة أنه مع زيادة عدد مرات مرور المرشح ، ينخفض ​​مستوى الضوضاء. ولكن هذا يقلل أيضًا من وضوح الصورة. هذه مشكلة معروفة مع عوامل التصفية الخطية. لكن طريقة تقليل الصورة الخاصة بنا لا تدعي أنها مثالية: هذا مجرد عرض لقدرات NumPy على تطبيق الإلتواء بدون تكرار.

الآن ، لنرى الإلتواء الذي تتشابه به حباتنا. للقيام بذلك ، سنخضع دفعة وحدة واحدة لتحولات مماثلة وتصور. في الواقع ، لن يكون الدافع منفردًا ، ولكن يساوي في السعة 255 ، نظرًا لأن الخلط نفسه هو الأمثل للبيانات الصحيحة. لكن هذا لا يتعارض مع تقييم المظهر العام للنواة:

 M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show() 

نظرنا بعيدًا عن مجموعة كاملة من ميزات NumPy ، وآمل أن يكون هذا كافياً لإظهار القوة الكاملة والجمال لهذه الأداة!

<أعلى>