في الآونة الأخيرة ، تم تحميل مقال بعنوان "
إعادة القياس العصبي يحسن التحسين الهيكلي " ، مقالة تحمل عنوان غير مثير للفضول ، وقد تم تحميلها على arXiv.org [arXiv: 1909.04240]. ومع ذلك ، اتضح أن المؤلفين ، في الواقع ، توصلوا ووصفوا طريقة غير تافهة للغاية لاستخدام شبكة عصبية للحصول على حل لمشكلة التحسين الهيكلي / الطوبولوجي للنماذج الفيزيائية (على الرغم من أن المؤلفين أنفسهم يقولون إن الطريقة أكثر عالمية). هذا النهج غريب للغاية ومثمر ، ويبدو أنه جديد تمامًا (ومع ذلك ، لا يمكنني أن أؤكد على هذا الأخير ، لكن لا مؤلفي العمل ، ولا مجتمع ODS ، ولا يمكنني أن أذكر النظير) ، لذلك قد يكون من المفيد معرفة المهتمين باستخدام الشبكات العصبية ، وكذلك حل مشاكل التحسين المختلفة.
عن ماذا تتحدث ما هي مهمة التحسين الطوبولوجي؟
فقط تخيل ما تحتاجه ، على سبيل المثال ، لتصميم خيط من الجسر ، أو مبنى متعدد الطوابق ، أو جناح طائرة ، أو شفرة التوربينات ، أو أي شيء آخر. عادةً ما يتم حل ذلك عن طريق العثور على أخصائي ، على سبيل المثال ، مهندس معماري ، باستخدام معرفته بالمتان ، والسوبرومات ، والمنطقة المستهدفة ، بالإضافة إلى خبرته ، والحدس ، وتخطيطات الاختبار ، إلخ. إلخ سيخلق المشروع المطلوب. من المهم هنا أن هذا المشروع الذي تم استلامه سيكون جيدًا فقط لأفضل هذا المتخصص. وهذا ، بالطبع ، لا يكفي دائمًا. لذلك ، عندما أصبحت أجهزة الكمبيوتر قوية بما فيه الكفاية ، بدأنا في محاولة تحويل هذه المهام إليها. لأنه
من الواضح ما يمكن للكمبيوتر الاحتفاظ به في الذاكرة وقصر الدارة ... لم لا؟
وتسمى هذه المهام "مشاكل التحسين الهيكلي" ، أي توليد التصميم الأمثل للهياكل الميكانيكية الحاملة [1]. الجزء الفرعي من مشاكل التحسين الهيكلي هو مشاكل التحسين
الطوبولوجي (في الواقع ، يركز العمل المعني بشكل خاص عليها ، لكن هذا ليس هو الأساس ، وأكثر من ذلك في وقت لاحق). تبدو مشكلة التحسين الطوبولوجي النموذجية مثل هذا: بالنسبة لمفهوم معين (جسر ، منزل ، إلخ) في الفضاء بأبعاد أو ثلاثة أبعاد ، مع وجود قيود محددة في شكل مواد وتقنيات ومتطلبات أخرى ، مع وجود بعض الأحمال الخارجية ، تحتاج إلى تصميم هيكل مثالي من شأنه أن يحمل الأحمال ويلبي القيود.
- "التصميم" يعني في الأساس إيجاد / وصف مساحة فرعية لمساحة المصدر التي يجب ملؤها بمواد البناء.
- يمكن التعبير عن الأمثلية ، على سبيل المثال ، في شكل شرط لتقليل الوزن الكلي للهيكل تحت قيود في شكل أقصى قدر من الضغوط المسموح بها في المواد وعمليات التشريد المحتملة في أحمال معينة.
لحل هذه المشكلة على جهاز كمبيوتر ، يتم أخذ عينات من مساحة الحل المستهدف في مجموعة من العناصر المحددة (بكسلات ثنائية الأبعاد وفوكسيل ثلاثية الأبعاد) ، وبعد استخدام بعض الخوارزمية ، يقرر الكمبيوتر ما إذا كان سيتم تعبئة هذا العنصر الفردي بمادة أو تركه فارغًا؟

(صورة من "التطورات في طوبولوجيا وتحسين الشكل" ، تشاو هوي لو ، 2010)
لذلك ، من بيان المشكلة بالفعل ، من الواضح أن حلها هو منشقة كبيرة للعلماء. أستطيع أن أقدم لأولئك الذين يرغبون في الحصول على بعض التفاصيل ، على سبيل المثال ، إلقاء نظرة على واحدة قديمة للغاية (2010 ، والتي لا تزال هناك الكثير بالنسبة لمجال تطوير نشط) ، ولكن أطروحة Chau Hoai Le مفصلة إلى حد ما وسهلة الاستخدام بعنوان "التطورات في الطوبولوجيا وتحسين الأشكال" [2] ، حيث سرقت الصور العلوية والسفلية.
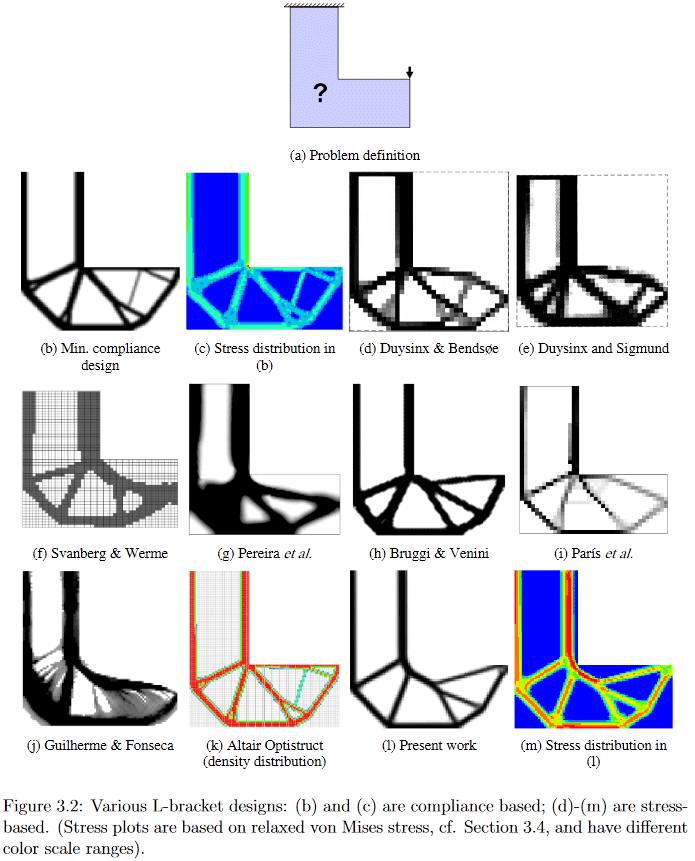
(صورة من "التطورات في طوبولوجيا وتحسين الشكل" ، تشاو هوي لو ، 2010)
على سبيل المثال ، في هذه الصورة يمكنك أن ترى بوضوح كيف تولد خوارزميات مختلفة تمامًا حلاً لمشكلة التصميم التي تبدو بسيطة للتعليق على شكل حرف L.
لذا ، عد الآن إلى العمل المعني.
اقترح المؤلفون بارعًا للغاية حل مشكلات التحسين هذه عن طريق إنشاء حل مرشح بواسطة شبكة عصبية والتطور اللاحق للحل عن طريق أساليب النسب المتدرجة فيما يتعلق بوظيفة الامتثال الموضوعية. يتم تقدير امتثال الهيكل الناتج باستخدام نموذج مادي قابل للتمييز ، والذي ، في الواقع ، يسمح باستخدام النسب المتدرج. وفقًا لهما (قام المؤلفون بنشر
الأكواد المصدر لـ [5]) ، فإن هذا يعطي نفس النتيجة مثل أفضل الخوارزميات التقليدية للمشاكل البسيطة ، أو أفضل هذه الخوارزميات المستخدمة كخطوط أساس ، لتلك المعقدة.
طريقة
بعد ذلك ، سأحاول وصف ما وكيف بالضبط اقترح المؤلفون القيام به ، لكنني أحذر على الفور من أنني لا أضمن صحة 100٪ ، لأنه بالإضافة إلى سعة الاطلاع الصاخبة للغاية في الحقل ، يجب أن أضيف ، بالإضافة إلى الإيجاز الضئيل للغاية في الوصف ، بعض "عدم النضج" العام للمادة ، التي ، بناءً على وجود طبعتين في 4 أيام ، هي في طور الانتهاء منها (
أضيف: في هذه اللحظة ، أعتقد أنه ، على الأقل ، بشكل أساسي ، يتم وصف كل شيء بشكل صحيح).
يتبع المؤلفون عمومًا النهج المتبع في حل مشكلات التحسين هذه ، ويطلق عليهم "طريقة SIMP المعدلة" ، والموصوفة بالتفصيل في [3] "تحسين طوبولوجيا فعال في MATLAB باستخدام 88 سطرًا من الكود". يمكن العثور على طباعة هذا العمل والرمز المرتبط به على
الموقع http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in-MATLAB . غالبًا ما يتم استخدام هذا العمل لبدء تعليم الطلاب حول مشكلات تحسين الطوبولوجيا ، وبالتالي ، من أجل فهمها بشكل أفضل ، يوصى بالتعرف عليها.
في "SIMP المعدل" ، يتم تحسين الحل مباشرة عن طريق تعديل وحدات البكسل في صورة الكثافة المادية. لم يقترح مؤلفو الورقة تعديل الصورة مباشرة (على الرغم من أن هذه الخوارزمية ، مع تساوي الأشياء الأخرى ، كانت خاضعة للتحكم) ، ولكن لتغيير معلمات ومدخلات الشبكة العصبية التلافيفية التي تولد صورة للكثافة المادية. إليك كيف تبدو الطريقة بأكملها عالميًا:

(صورة من المنشور المعني)
الخطوة 1 ، توليد مرشح
شبكة عصبية (يشار إليها فيما يلي باسم NS) باستخدام متجه الإدخال الأساسي العشوائي _ بيتا (مثل وزن الشبكة ، هي معلمة مدربة) ، وتولد (بعض) صورة للحل (تعمل مع 2D ، ولكن في 3D ، أعتقد أنه يمكن أيضًا توزيعها ). يستخدم جزء الاختزال في بنية U-Net المعروفة كمولد NS.
الخطوة 2 ، تطبيق القيود وتحويل المرشح إلى إطار نموذج مادي
يتم تحويل قيم البكسل إلى كثافات مادية في خطوتين:
- أولاً ، في خطوة واحدة ، يتم حل مشكلة تطبيع القيم غير المقيسة للبكسل الذي تم إنشاؤه (تم تصميم NS بحيث يتم إخراج ما يسمى logits - القيم في النطاق (-inf ، + inf)) وتطبيق قيود على المبلغ الإجمالي للحل الناتج. لهذا ، يتم تطبيق السيني - عنصرًا حكيمًا على الصورة ، حيث يتم تغيير وسيطة من خلال ثابت اعتمادًا على الصورة التي يتم تحويلها وحجم الحل المطلوب (يتم تحديد قيمة ثابت الثبات هذا عن طريق البحث الثنائي بحيث يكون إجمالي حجم الكثافة التي تم الحصول عليها بذلك مساوياً لوحدة تخزين محددة مسبقًا V0). تحليل مفصل لهذه المرحلة ، انظر التعليق ) ؛
- علاوة على ذلك ، تتم معالجة الصورة الطبيعية الناتجة لكثافة الهيكل بواسطة ما يسمى مرشح الكثافة بنصف قطر 2. بعبارات أكثر شهرة ، هذا المرشح ليس أكثر من المتوسط المرجح الطبيعي للنقاط المجاورة في الصورة. يمكن تمثيل الأوزان الموجودة في هذا الفلتر (قلب المرشح) كقيم لارتفاعات النقاط الموجودة على سطح مخروط منتظم ملقى على المستوى بحيث يكون رأسه عند النقطة الحالية ، لذلك يسميه المؤلفون بأنه مخروط مرشح (بمزيد من التفاصيل حول هذا الموضوع انظر وصف مرشح الكثافة في الفصل 2.3. ترشيح [3]).
باختصار ، يتمثل جوهر الخطوة 2 بأكملها في أن الناتج غير الطبيعي من NS عادي تمامًا يتحول إلى إطار طبيعي ومملس قليلاً من النموذج المادي (مجموعة من الكثافات المادية للعناصر) ، والتي تم بالفعل تطبيق القيود المسبقة الضرورية عليها (هذه هي كمية المادة المستخدمة).
الخطوة 3 ، وتقييم النموذج المادي الناتج الإطار
يتم تشغيل الإطار الناتج من خلال محرك مادي قابل للتمييز للحصول على ناقل (/ tensor؟) للإزاحة الهيكلية تحت الحمل (بما في ذلك الجاذبية) U. المفتاح هنا هو تمايز المحرك ، والذي يسمح لنا بالحصول على التدرجات (أذكر أن تدرج الوظيفة عمومًا موتر مكون من مشتقات جزئية للدالة فيما يتعلق بجميع الحجج الخاصة بها. يوضح التدرج اتجاه ومعدل تغيير الوظيفة في النقطة الحالية ، وبالتالي ، يمكنك معرفة "تطور" الوسيطات بحيث يحدث التغيير المطلوب مع الدالة مثل - انخفض أو زاد). لا يحتاج هذا المحرك المادي القابل للتمييز إلى أن يكون مكتوبًا من نقطة الصفر - لقد ظل موجودًا لفترة طويلة ومعروفًا تمامًا. احتاج المؤلفون فقط إلى عمل الاقتران بحزم حساب الشبكة العصبية ، مثل TensorFlow / PyTorch.
الخطوة 4 ، حساب قيمة الوظيفة الهدف للإطار السلكي / المرشح
يتم حساب دالة الهدف العددية c (x) التي يجب تقليلها ، والتي تصف الامتثال (هو عكس الصلابة) للإطار الناتج. تعتمد وظيفة الامتثال على ناقل الحركة U الذي تم الحصول عليه في الخطوة الأخيرة ومصفوفة الصلابة للهيكل K (ليس لدي معرفة كافية بتحسين الطوبولوجيا لفهم من أين تأتي K - سأفترض أنه يبدو أنه تم أخذها في الاعتبار بشكل مباشر من الإطار).
/ *
انظر أيضًا التعليقات
(1) من
kxx و
(2) من
350 Stealth ، على الرغم من أن التنوير الأساسي يستحق الذهاب إلى العمل [3].
* /
وبعد ذلك يتم ذلك. نظرًا لأن كل شيء يتم إنشاؤه في بيئة تتميز بالتمايز التلقائي ، في هذه المرحلة ، نحصل تلقائيًا على جميع التدرجات للوظيفة الموضوعية ، والتي يتم دفعها بسبب تباين جميع التحويلات في كل خطوة إلى الأوزان ومتجه إدخال الشبكة العصبية المولدة. الأوزان ومتجه المدخلات ، على التوالي ، مع مشتقاتهما الجزئية ، تتغير ، مما تسبب في التغيير اللازم - التقليل إلى أدنى حد من الوظيفة الهدف. بعد ذلك ، تحدث دورة جديدة من المرور المباشر عبر NS -> تطبيق القيود -> حساب النموذج المادي -> حساب الوظيفة الهدف -> تدرجات جديدة وتحديث الأوزان. وهكذا حتى تقارب ألغو.
هناك نقطة مهمة ، الوصف الذي لم أجده في العمل ، تتمثل في كيفية اختيار الحجم الإجمالي للبناء V0 ، بمساعدة تحويل الحل المرشح إلى إطار العمل في الخطوة 2. من الواضح أن خصائص الحل الناتج تعتمد إلى حد كبير على اختياره. من خلال المؤشرات غير المباشرة (تحتوي جميع أمثلة الحلول التي تم الحصول عليها [4] على العديد من الحالات التي تختلف بدقة في الحد من حجم الصوت) ، أفترض أنها ببساطة إصلاح V0 على شبكة معينة من النطاق [0.05 ، 0.5] وبعد ذلك ينظرون إلى الحلول التي تم الحصول عليها بعيون مختلفة V0. حسنًا ، بالنسبة للعمل المفاهيمي ، فإن هذا ، بشكل عام ، يكفي ، على الرغم من أنه بالطبع سيكون من المثير للاهتمام للغاية رؤية خيار مع اختيار V0 هذا أيضًا ، لكن من المحتمل أن ينتقل إلى المرحلة التالية من تطوير العمل.
النقطة المهمة الثانية ، التي لم أفهمها ، هي كيفية فرض قيود / متطلبات على نوع معين من الحل. أي إذا كان لا يزال بإمكانك فصل الجسر عن المبنى بفضل النموذج المادي (يحظى المبنى بالدعم الكامل ، والجسر هو فقط في نهايات الحدود) ، فكيف يمكن فصل مبنى من 3 طوابق عن مبنى مكون من 4 طوابق؟
كيف يعمل؟
اتضح أنه بالنسبة للمشكلات الصغيرة (من حيث حجم مساحة الحل = عدد البكسل) ، فإن الطريقة تعطي quality نفس جودة النتائج مثل أفضل الطرق التقليدية للتحسين الطوبولوجي ، ولكن على الطرق الكبيرة (حجم الشبكة من 2 ^ 15 بكسل أو أكثر ، أي ، على سبيل المثال ، من 128 * 256 وأكثر) الحصول على حلول عالية الجودة من خلال الطريقة هو أكثر احتمالا من أفضل الحلول التقليدية (من بين 116 مشكلة تم اختبارها ، أعطت الطريقة حلاً مفضلاً في 99 مشكلة ، مقابل 66 مشكلة مفضلة في أفضل مشكلة تقليدية).
علاوة على ذلك ، هنا يبدأ شيء مثير للاهتمام بشكل خاص. تعاني الطرق التقليدية للتحسين الطوبولوجي في المشكلات الكبيرة من حقيقة أنها في المراحل المبكرة من العمل تشكل بسرعة شبكة صغيرة الحجم ، والتي تتداخل بعد ذلك مع تطور الهياكل واسعة النطاق. هذا يؤدي إلى حقيقة أن النتيجة التي تم الحصول عليها صعبة / من المستحيل تنفيذها جسديا. لذلك ، هناك اتجاه كامل في مشاكل تحسين الهيكل الذي يدرس / يأتي بطرق لكيفية جعل الحلول الناتجة أكثر ملاءمة من الناحية التكنولوجية.
هنا ، على ما يبدو ، بفضل شبكة الالتفاف ، يحدث التحسين في وقت واحد على عدة مستويات مكانية في نفس الوقت ، مما يسمح بتجنب / تقليل "الويب" بشكل كبير والحصول على حلول أكثر بساطة ، ولكن عالية الجودة وصديقة للتكنولوجيا!
بالإضافة إلى ذلك ، مرة أخرى بفضل الالتفاف في الشبكة ، يتم الحصول على حلول مختلفة اختلافًا جوهريًا عن الطرق التقليدية التقليدية.
على سبيل المثال ، في التصاميم:
- وجدت طريقة شعاع ناتئ حلا من 8 مكونات فقط ، في حين أن أفضل التقليدية - 18.
- اخترت طريقة الجسر الرفيع للدعم دعماً واحداً بنمط متفرّع يشبه الأشجار ، في حين أن الطريقة التقليدية للدعم اثنين - الدعم
- تستخدم طريقة السقف أعمدة ، بينما تستخدم الطريقة التقليدية نمطًا متفرّعًا. إلخ
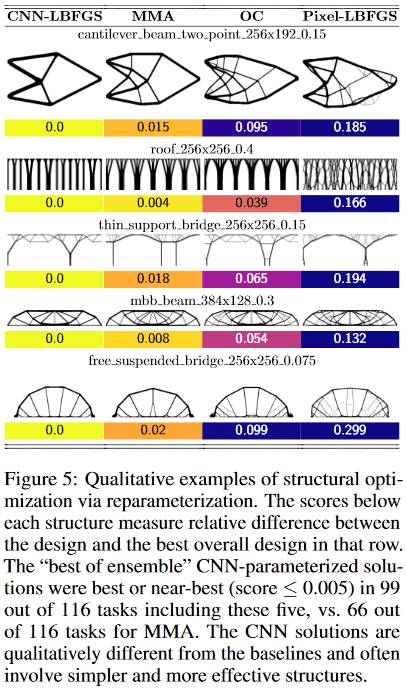
(صورة من المنشور المعني)
ما هو خاص جدا حول هذا العمل؟
لم أر مثل هذا الاستخدام للشبكة العصبية. عادة ، يتم استخدام الشبكات العصبية للحصول على وظيفة معقدة للغاية ومعقدة y = F (x ، ثيتا) (حيث x عبارة عن وسيطة ، والثيتا هي معلمات مخصصة) ، والتي يمكن أن تفعل شيئًا مفيدًا. على سبيل المثال ، إذا كانت x صورة من كاميرا سيارة ، يمكن أن تكون قيمة الدالة y ، على سبيل المثال ، علامة على وجود مشاة بالقرب من السيارة بشكل خطير. أي من المهم هنا أن يكون نوع الوظيفة نفسه ، والذي يتم استخدامه مرارًا وتكرارًا لحل مشكلة ما ، ذا قيمة.
هنا ، يتم استخدام الشبكة العصبية كمضبط مستودع معدل الماكرة لمعلمات بعض النماذج المادية ، والتي بسبب بنيتها المعمارية ذاتها ، تفرض قيودًا معينة على قيم وأشكال التغييرات في هذه المعلمات (في الواقع ، تعد الأمثلة تحت عنوان Pixel-LBFGS محاولة لتحسين البكسل مباشرةً ، وليس باستخدام شبكة عصبية لتوليدها ، تكون النتائج واضحة ، NS مهم). هذا هو المكان الذي يصبح فيه تداخل الشبكة العصبية المستخدمة أمرًا بالغ الأهمية ، لأن بنيانها يتيح لك "التقاط" مفهوم نقل الثقل وقليلا من التدوير (تخيل أنك تتعرف على نص من صورة - من المهم بالنسبة لك استخراج النص ولا يهم أيًا أجزاء من الصورة ، وهي موجودة وكيف يتم تدويرها - أي أنك تحتاج إلى ثبات في النقل والدوران). في هذه المشكلة ، لا يزال هناك نوع من العصي المادية ، وهي وحدة هيكلية وكثير منها نقوم بتحسينها ، بغض النظر عن موقعها واتجاهها في الفضاء.
على سبيل المثال ، قد لا تعمل شبكة كلاسيكية متصلة بالكامل ، هنا (بنفس القدر من الجودة) ، لأن بنيتها تسمح بالكثير / الصغير (جيدًا ، نعم ، مثل ثنائية ، كيف تبدو). في الوقت نفسه ، على الرغم من حقيقة أن NS لا يزال هنا وظيفة صعبة للغاية ومعقدة جدا y = F (x ، ثيتا) ، في هذه المهمة لا نعطي في نهاية المطاف لعنة حول حجتها x أو معالمها theta ، وكيف سيتم استخدام الوظيفة. نحن نهتم فقط بقيمتها الفردية y ، والتي يتم الحصول عليها في عملية تحسين وظيفة موضوعية محددة لنموذج مادي واحد محدد ، حيث {x ، theta} هي مجرد معلمات قابلة للتخصيص!
هذا ، في رأيي ، هو فكرة رائعة وجديدة بذهول! (على الرغم من ذلك ، بالطبع ، كما هو الحال دائمًا ، فقد يتضح أن شميدهوبر قد وصفها مرة أخرى في أوائل التسعينيات ، لكننا سننتظر ونرى)
بشكل عام ، فإن معنى الطريقة يشبه إلى حد ما التعلم المعزز - حيث يتم استخدام NS ، بشكل تقريبي ، "كمستودع للخبرة" للعامل الذي يتصرف في بيئة معينة ، والذي يتم تحديثه عندما تتلقى البيئة تعليقات على تصرفات الوكيل. هناك فقط ، يتم استخدام "مستودع الخبرة" هذا دائمًا في اتخاذ القرارات الجديدة من قِبل الوكيل ، وهو هنا مجرد مستودع لمعلمات النموذج المادي ، الذي نهتم به فقط بالنتيجة النهائية الوحيدة للتحسين.
حسنا ، الماضي. لحظة مثيرة اشتعلت عيني.
هذه هي الطريقة التي تبدو بها الحلول المثلى لمهمة بناء متعدد الطوابق:
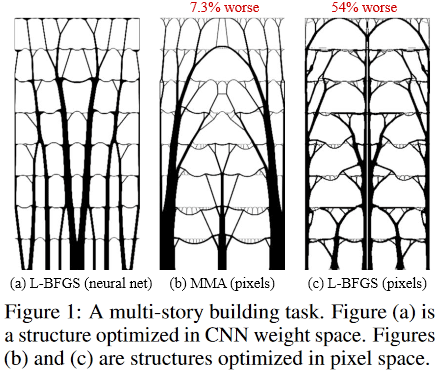
(صورة من المنشور المعني)
و هكذا:

يقع داخل كنيسة العائلة المقدسة الرائعة ، معبد العائلة المقدسة ، الذي يقع في برشلونة ، إسبانيا ، والذي تم تصميمه من قبل أنطونيو غاودي الرائع.
شكر
أشكر المؤلف الأول للمقالة ، ستيفان هوير ، على المساعدة العاجلة في توضيح بعض التفاصيل الغامضة عن العمل ، وكذلك مشاركي هبر الذين قدموا إضافاتهم و / أو أفكارهم الاستفزازية المفيدة.
[1]
خيار لتحديد مشكلة التحسين الهيكلية / الطوبولوجية[2]
"التطورات في الطوبولوجيا وتحسين الشكل"[3] Andreassen، E.، Clausen، A.، Schevenels، M.، Lazarov، BS، and Sigmund، O. Efficient Optology optimization in MATLAB وذلك باستخدام 88 سطر من الكود. التحسين الهيكلي والمتعدد التخصصات ، 43 (1): 1-16 ، 2011. تتوفر نسخة مسبقة من هذا العمل والرمز على
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in -MATLAB[4]
أمثلة لحلول العمل[5] مصدر رموز العمل:
https://github.com/google-research/neural-structural-optimization
انظر أيضا
آخر تحديث لهذا المنشور 2020.01.23 09:18