Arend - لغة الكتابة المعتمدة على بروتوكول HoTT (الجزء 1)

في هذا المنشور ، سنتحدث عن لغة JetBrains التي تم إصدارها حديثًا مع الأنواع المعتمدة من Arend (تم تسمية اللغة باسم Gating Rent ). تم تطوير هذه اللغة بواسطة JetBrains Research خلال السنوات القليلة الماضية. على الرغم من إتاحة المستودعات قبل عام بشكل عام على github.com/JetBrains ، إلا أن الإصدار الكامل من Arend لم يحدث إلا في يوليو من هذا العام.

سنحاول معرفة كيف يختلف Arend عن الأنظمة الحالية للرياضيات النظامية استنادًا إلى الأنواع التابعة ، والوظائف المتوفرة الآن لمستخدميها. نحن نفترض أن قارئ هذه المقالة معتادًا بشكل عام على الأنواع التابعة وقد سمع واحدة على الأقل من اللغات المعتمدة على أنواع تابعة: Agda أو Idris أو Coq أو Lean. ومع ذلك ، لا نتوقع أن يكون للقارئ أنواع تابعة في مستوى متقدم.

من أجل البساطة والاطمئنان ، سترافق قصتنا حول أنواع Arend و homotopy عن طريق تطبيق Arend لأبسط خوارزميات فرز القائمة - حتى مع هذا المثال ، يمكنك أن تشعر بالفرق بين Arend و Agda و Coq. يوجد بالفعل عدد من المقالات حول Habré المخصصة للأنواع التابعة. دعنا نقول عن تنفيذ قوائم الفرز باستخدام طريقة QuickSort على Agda هناك مثل هذه المقالة . سنقوم بتنفيذ خوارزمية أبسط لفرز إدراج. في هذه الحالة ، سوف نركز على إنشاءات لغة Arend ، وليس على خوارزمية الفرز نفسها.

لذلك ، فإن الاختلاف الرئيسي بين Arend واللغات الأخرى ذات الأنواع التابعة هو النظرية المنطقية التي تقوم عليها. يستخدم Arend هكذا نظرية نوع homotopy V. Voevodsky المكتشفة حديثًا. بشكل أكثر تحديدًا ، يعتمد Arend على صيغة HTT تسمى "نظرية الكتابة ذات التباعد". تذكر أن Coq يستند إلى ما يسمى بحساب التفاضل والتكامل للإنشاءات الاستقرائي (حساب التفاضل والتكامل للإنشاءات الاستقرائية) ، في حين تستند Agda و Idris على نظرية Martin-Löf المكثفة للأنواع . حقيقة أن Arend يعتمد على HoTT تؤثر بشكل كبير على الإنشاءات النحوية وتشغيل خوارزمية التحقق من النوع (typcheker). سنناقش هذه الميزات في هذه المقالة.

دعنا نحاول أن تصف بإيجاز حالة البنية الأساسية للغات. بالنسبة إلى Arend ، يوجد مكون إضافي لبرنامج IntelliJ IDEA ، والذي يمكن تثبيته مباشرة من مستودع إضافات IDEA. من حيث المبدأ ، يكفي تثبيت المكوّن الإضافي للعمل بشكل كامل مع Arend ، لا تزال لا تحتاج إلى تنزيل وتثبيت أي شيء. بالإضافة إلى التحقق من الكتابة ، يوفر البرنامج المساعد Arend وظيفة مألوفة لمستخدمي IDEA: هناك تسليط الضوء على ومواءمة التعليمات البرمجية ، مختلف refactorings والنصائح. هناك أيضًا خيار استخدام إصدار وحدة التحكم من Arend. يمكن العثور هنا على وصف أكثر تفصيلاً لعملية التثبيت.

تستند أمثلة التعليمات البرمجية في هذه المقالة إلى مكتبة Arend القياسية ، لذلك نوصي بتنزيل التعليمات البرمجية المصدر الخاصة بها من المستودع . بعد التنزيل ، يجب استيراد الدليل المصدر كمشروع IDEA باستخدام أمر استيراد المشروع. في Arend ، تم بالفعل إضفاء الطابع الرسمي على بعض أقسام نظرية نوع homotopy ونظرية الحلقة. على سبيل المثال ، في المكتبة القياسية ، يتم تنفيذ سلسلة الأعداد المنطقية Q مع أدلة جميع الخصائص النظرية المطلوبة.

وثائق اللغة التفصيلية ، التي يتم فيها شرح الكثير من النقاط التي تتناولها هذه المقالة بمزيد من التفصيل ، هي أيضًا في المجال العام. يمكنك طرح الأسئلة مباشرة على مطوري Arend في قناة التلغراف .

1. نظرة عامة على HoTT / Arend

نظرية نوع Homotopy (أو باختصار HoTT) هي نوع من نظرية النوع المكثف التي تختلف عن نظرية النوع Martin-Löf الكلاسيكية (MLTT ، التي تستند إليها Agda) وحساب التفاضل والتكامل الاستقرائي (CIC ، الذي يستند إليه Coq) ، تحتوي البيانات والمجموعات على الأنواع المسماة بمستوى homotopy العالي.

في هذا المقال ، لا نضع أنفسنا هدفًا لشرح أسس HoTT بالتفصيل - من أجل عرض تفصيلي لهذه النظرية ، سيكون من الضروري إعادة كتابة الكتاب بالكامل (انظر هذا المنشور ). نلاحظ فقط أن النظرية القائمة على البديهيات في HoTT ، إلى حد ما ، أكثر أناقة وإثارة للاهتمام من نظرية النوع مارتن لووف الكلاسيكية. وبالتالي ، فإن عددًا من البديهيات التي كان لابد من فرضها مسبقًا (على سبيل المثال ، الإمتداد الوظيفي) قد ثبت في HoTT كنظريات. بالإضافة إلى ذلك ، في HoTT ، يمكن للمرء تحديد مجالات homotopy متعددة الأبعاد داخليًا وحتى حساب بعض مجموعات homotopy الخاصة بهم.

ومع ذلك ، فإن هذه الجوانب من HoTT مثيرة للاهتمام في المقام الأول لعلماء الرياضيات ، والغرض من هذه المقالة هو شرح كيف يقارن Arend المستندة إلى HoTT بشكل إيجابي مع Agda / MLTT و Coq / CIC من خلال مثال تمثيل مثل بسيط ومألوف لأي كيانات مبرمج. عند قراءة هذا المقال ، يكفي أن نعامل HoTT كنوع من نظرية النوع المكثف مع بديهيات أكثر تطوراً ، مما يعطي الراحة عند العمل مع الأكوان والمساواة.

1.1 الأنواع التابعة ، مراسلة كاري - هوارد ، الأكوان

تذكر أن اللغات ذات الأنواع التابعة تختلف عن لغات البرمجة الوظيفية العادية في ذلك بالإضافة إلى أنواع البيانات المعتادة ، مثل القوائم أو الأرقام الطبيعية ، هناك أنواع تعتمد على قيمة المعلمة. أبسط الأمثلة على هذه الأنواع هي متجهات بطول معين n أو أشجار متوازنة بعمق معين d. تم ذكر بعض الأمثلة الإضافية على هذه الأنواع هنا.

تذكر أن مراسلات Curry - Howard تسمح للمرء بتفسير عبارات المنطق كأنواع تابعة. الفكرة الرئيسية لهذه المراسلات هي أن النوع الفارغ يتوافق مع بيان خاطئ ، وأنواع السكان المأهولة تتوافق مع عبارة حقيقية. يمكن اعتبار عناصر الكتابة كدليل على البيان المنطقي المقابل. على سبيل المثال ، يمكن اعتبار أي عنصر مثل الأعداد الصحيحة كدليل على حقيقة وجود أعداد صحيحة (أي ، يتم ملء نوع الأعداد الصحيحة).

تتوافق الإنشاءات الطبيعية المختلفة على الأنواع مع روابط منطقية مختلفة:

• يُطلق على منتج النوعين A × B أحيانًا نوع الزوج Pair A B. نظرًا لأن هذا النوع يتم تعبئته في حالة ملء كلا النوعين A و B فقط ، فإن هذا البناء يتوافق مع المنطق "و".
• مجموع الأنواع A + B. في Haskell ، يسمى هذا النوع إما A B. حيث أن هذا النوع ممتلئ إذا وفقط إذا كان أحد الأنواع A أو B ، فإن هذا البناء يتوافق مع منطقية "أو".
  
• نوع وظيفي A → B. أي وظيفة من هذا النوع تحول عناصر A إلى عناصر B. وبالتالي ، فإن هذه الوظيفة موجودة بالضبط عندما يعني وجود عنصر من النوع A وجود عنصر من النوع B. لذلك ، فإن هذا البناء يتوافق مع الآثار الضمنية.
  

لنفترض الآن أننا حصلنا على نوع معين A ومجموعة من الأنواع B ذات معلمات بعنصر a من النوع A. فلنقدم أمثلة على إنشاءات أكثر تعقيدًا على أنواع تابعة.

• نوع الوظيفة التابعة Π (a: A) (B a). يتزامن هذا النوع مع النوع الوظيفي المعتاد A → B إذا كانت B مستقلة عن A. وظيفة من النوع Π (a: A) (B a) تحول أي عنصر a من النوع A إلى عنصر من النوع B a. وهكذا ، توجد مثل هذه الوظيفة إذا كان هناك عنصر B a. لذلك ، هذا البناء يتوافق مع الكمي العالمي ∀. بالنسبة للنوع الوظيفي التابع ، يستخدم Arend بناء الجملة \Pi (x : A) -> B a ، ويمكن بناء المصطلح الذي يسكن هذا النوع باستخدام تعبير lambda \lam (a : A) => f a.
• نوع الأزواج التابعة هو Σ (a: A) (B a). يتزامن هذا النوع مع الأنواع المعتادة من أزواج A × B إذا كانت B مستقلة عن A. يتم ملء النوع a (a: A) (B a) بالضبط عند وجود عنصر a: A وعنصر من النوع B a. وبالتالي ، فإن هذا النوع يتوافق مع ∃ وجود ∃ . تتم الإشارة إلى نوع الأزواج التابعة في Arend بواسطة \Sigma (a : A) (B a) ، ويتم إنشاء المصطلحات التي تسكنها باستخدام مُنشئ الزوج (a, b) التابع) (a, b) .
  
• نوع المساواة هو a = a '، حيث a و a' عنصران من نوع A. يتم ملء هذا النوع إذا كانت a و a 'متساوية ، فارغة. من الواضح أن هذا النوع هو تناظر للمساواة في المنطق.

في هذه المرحلة ، نحيل القارئ إلى المصادر التي تناقش فيها مراسلات كاري - هاورد بمزيد من التفصيل (انظر ، على سبيل المثال ، مجموعة من المحاضرات أو المقالات هنا أو هنا ).

يجب أن تحتوي كل التعبيرات التي تم بحثها في نظرية النوع على نوع ما. نظرًا لأن التعبيرات التي تشير إلى الأنواع تُعتبر أيضًا في إطار هذه النظرية ، فإنها تحتاج أيضًا إلى تعيين نوع معين. والسؤال هو ، أي نوع من أنواع ينبغي أن يكون؟

أول قرار ساذج يتبادر إلى الذهن هو تخصيص نوع رسمي لكل الأنواع ، يسمى الكون (يطلق عليه ذلك لأنه يحتوي على جميع الأنواع بشكل عام). إذا استخدمنا هذا الكون ، فستتلقى إنشاءات المبلغ ونوع المنتجات المذكورة أعلاه التوقيع \Type → \Type → \Type ، والإنشاءات الأكثر تعقيدًا للمنتج التابع وسيحصل المجموع التابع على التوقيع Π (A : \Type) → ((A → \Type) → \Type) .

عند هذه النقطة ، يطرح السؤال ، ما نوع يجب أن يكون \Type الكون نفسه؟ محاولة ساذجة للقول إن نوع الكون \Type ، بحكم تعريفه ، هو \Type نفسه يؤدي إلى مفارقة جيرارد ، لذلك بدلاً من كون واحد \Type ضع في الاعتبار التسلسل الهرمي اللانهائي للكون ، أي السلسلة المتداخلة من الأكوان \Type 1 < \Type 2 < … ، والتي يتم ترقيم مستوياتها بالأرقام الطبيعية ، ونوع الكون \Type i ، بحكم التعريف ، هو الكون \Type (i+1) . بالنسبة للإنشاءات المذكورة أعلاه ، يجب أيضًا تقديم توقيعات أكثر تعقيدًا .

وبالتالي ، هناك حاجة الأكوان في نظرية النوع بحيث أي تعبير له نوع معين. في بعض أنواع نظرية النوع ، تستخدم الأكوان لغرض آخر: التمييز بين أنواع الأنواع. لقد رأينا بالفعل أن المجموعات والبيانات هي حالات خاصة بأنواعها. هذا يدل على أنه قد يكون من المنطقي أن ندخل في النظرية عالمًا منفصلاً للدعائم للبيانات وسلسلة هرمية منفصلة من أكوان Set _i للمجموعات. هذا هو بالضبط النهج المستخدم في حساب التفاضل والتكامل الإنشائي للإنشاءات ، وهي النظرية التي يقوم عليها نظام Coq.

1.2 أمثلة على أبسط أنواع الاستقراء والوظائف العودية

النظر في التعاريف على Arend من أبسط أنواع البيانات الاستقرائي: نوع منطقية ، ونوع الرقم الطبيعي ، وقوائم متعددة الأشكال. يستخدم Arend الكلمة الرئيسية \data لإدخال أنواع استقلالية جديدة.

\data Empty -- ,

\data Bool
| true
| false

\data Nat
| zero
| suc Nat

\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)

كما ترى من الأمثلة أعلاه ، بعد الكلمة الرئيسية \data ، تحتاج إلى تحديد اسم النوع الاستقرائي وقائمة منشئيها. في الوقت نفسه ، قد يحتوي نوع البيانات والمنشئين على بعض المعلمات. دعنا نقول في المثال أعلاه أن نوع List يحتوي على معلمة واحدة A nil يحتوي مُنشئ قائمة nil على أية معلمات ، كما أن المُنشئ: -: يحتوي على معلمتين (إحداها من النوع A ، والآخر من النوع List A ). يتكون الكون \Set من أنواع مجموعات (سيتم تحديد تعريف المجموعات في القسم التالي). \infixr تتيح لك استخدام تدوينات infix \infixr : -: بالإضافة إلى ذلك ، يخبر محلل Arend أن العامل: -: هو عملية ربط يمين ذات أولوية 5.

في Arend ، تبدأ جميع الكلمات الرئيسية بحرف خط مائل عكسي ("\") ، وهو تطبيق مستوحى من LaTeX. لاحظ فقط أن القواعد المعجمية في Arend هي متحررة جدًا: Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left وحتى n:Nat - كل هذه الحرف هي أمثلة Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left صحيحة في Arend. يوضح المثال الأخير مدى أهمية أن يتذكر مستخدم Arend وضع مسافات بين المعرفات وحروف النقطتين . لاحظ أنه في معرفات Arend ، لا يُسمح باستخدام أحرف Unicode (على وجه الخصوص ، لا يمكنك استخدام السيريلية).

يستخدم Arend الكلمة الأساسية \func لتحديد الوظائف. يكون بناء الجملة لهذا البناء كالتالي: بعد الكلمة الأساسية \func ، تحتاج إلى تحديد اسم الوظيفة ومعلماتها ونوع القيمة المرجعة. العنصر الأخير في تحديد الوظيفة هو جسمها.

إذا كان من الممكن تحديد التعبير الذي سيتم حساب الوظيفة المحددة فيه صراحة ، فمن أجل الإشارة إلى نص الوظيفة ، يتم استخدام الرمز المميز =>. خذ بعين الاعتبار ، على سبيل المثال ، تعريف دالة إلغاء النوع.

 \func Not (A : \Type) : \Type => A -> Empty 

لا يجب دائمًا تحديد نوع الإرجاع لوظيفة ما بشكل صريح. في المثال أعلاه ، سيكون Arend قادرًا على استنتاج النوع " Not بشكل مستقل ، ويمكننا حذف تعبير ": \Type " بعد الأقواس.

كما هو الحال في معظم أنظمة الرياضيات الرسمية ، لا يتعين على المستخدم تحديد مستوى تنبؤي صريح للكون \Type ، والتعاريف التي تستخدم فيها الأكوان دون تحديد مستوى تنبؤي بشكل صريح تعتبر متعددة الأشكال .

الآن دعونا نحاول تحديد وظيفة تحسب طول القائمة. هذه الوظيفة سهلة التحديد من خلال مطابقة الأنماط. يستخدم Arend الكلمة الرئيسية \elim لهذا. بعد ذلك ، يجب عليك تحديد المتغيرات التي يتم بها إجراء المقارنة (إذا كان هناك أكثر من متغير واحد ، فيجب كتابتها بفاصلة). إذا تم إجراء المقارنة لجميع المعلمات الصريحة ، فيمكن حذف \elim مع المتغيرات. يتبع ذلك كتلة من نقاط المقارنة ، مفصولة عن بعضها البعض بشريط عمودي "|". كل عنصر في هذه الكتلة هو تعبير عن النموذج «, » => «» .

 \func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs) 

في المثال أعلاه ، تحيط المعلمة A الخاصة بوظيفة length بأقواس مجعدة. تُستخدم الأقواس الموجودة في Arend للإشارة إلى الوسائط الضمنية ، أي الوسائط التي يمكن للمستخدم حذفها عند استدعاء وظيفة أو استخدام نوع. لاحظ أنه في Arend لا يمكنك استخدام تدوينات infix لتعيين المنشئات عند المطابقة مع نقش ، لذلك يتم استخدام تدوين البادئة في المثال النموذجي.

كما هو الحال في Coq / Agda ، في Arend ، يجب ضمان أن جميع الوظائف مكتملة (على سبيل المثال ، التحقق من الإنهاء موجود في Arend). في تعريف دالة الطول ، يكون هذا الفحص ناجحًا ، حيث إن المكالمة العودية تقلل بشكل صارم أول وسيطة صريحة. إذا لم يحدث هذا التخفيض ، فسوف يقدم Arend رسالة خطأ.

 \func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad 

يتيح Arend التبعيات الدائرية ووظائف العودية المتبادلة التي يتم أيضًا إجراء اختبارات إكمالها. يتم تنفيذ خوارزمية هذا الاختيار بناءً على مقالة أ. أبيل. ستجد فيه وصفًا أكثر تفصيلًا للشروط التي يجب أن تستوفيها العودية المتبادلة.

1.3 كيف تختلف المجموعات عن البيانات؟

سبق أن كتبنا أن أمثلة الأنواع هي مجموعات وبيانات. بالإضافة إلى ذلك ، استخدمنا الكلمات الرئيسية \Type و \Set للدلالة على الأكوان في أرند. سنحاول في هذا القسم أن نوضح بمزيد من التفصيل كيف تختلف العبارات عن المجموعات من حيث أنواع نظرية النوع المكثف (MLTT ، CIC ، HoTT) ، وفي نفس الوقت سنشرح معنى الكلمة الرئيسية \Prop و \Set و \Type in Arend.

تذكر أنه في نظرية مارتن لوف الكلاسيكية لا يوجد فصل بين الأنواع في مجموعات وبيانات. على وجه الخصوص ، من الناحية النظرية ، يوجد واحد فقط من الكون التراكمي (والذي تتم الإشارة إليه إما بواسطة Set في Agda أو Type in Idris أو Sort in Lean). هذا النهج هو أبسط ، ولكن هناك مواقف تتجلى فيها أوجه القصور فيها. لنفترض أننا نحاول تنفيذ نوع "القائمة المرتبة" كزوج تابع يتكون من قائمة وإثبات لترتيبها. اتضح بعد ذلك ، في إطار MLTT "النقي" ، لن يكون من الممكن إثبات المساواة في القوائم المرتبة التي تتكون من عناصر متطابقة ، والتي تختلف في الوقت نفسه من حيث إثبات الطلب. سيكون الحصول على مثل هذه المساواة أمرًا طبيعيًا ومرغوبًا فيه ، لذا فإن استحالة إثبات ذلك يمكن اعتبارها عيبًا نظريًا في MLTT.

في Agda ، يتم حل هذه المشكلة جزئيًا بمساعدة ما يسمى بملاحظات عدم الأهمية (راجع المصدر ، حيث تتم مناقشة مثال القائمة بمزيد من التفاصيل). ومع ذلك ، فإن هذه التعليقات التوضيحية ليست بناءً من نظرية MLTT ، كما أنها ليست بنيات كاملة على أنواع (من المستحيل وضع علامة مع تعليق توضيحي للنوع غير مستخدم في وسيطة الدالة).

في CIC ، استنادًا إلى CIC ، يوجد أكوان مختلفان متداخلان في بعضهما البعض: Prop (عالم العبارات) و Set (عالم المجموعات) ، وهما مغموران في التسلسل الهرمي الشامل لأكوان Type . الفرق الرئيسي بين Prop و Set هو وجود عدد من القيود على المتغيرات التي ينتمي نوعها إلى Prop في Coq. على سبيل المثال ، لا يمكن استخدامها في العمليات الحسابية ، والمقارنة مع العينة الخاصة بهم ممكنة فقط داخل دليل البيانات الأخرى. من ناحية أخرى ، جميع العناصر من النوع الذي ينتمي إلى عالم Prop متساوية في بديهية الأدلة غير المهمة ، انظر البيان في Coq.Logic.ProofIrrelibility . باستخدام هذه البديهية ، يمكننا بسهولة إثبات المساواة في القوائم المطلوبة المذكورة أعلاه.

أخيرًا ، فكر في مقاربة Arend / HoTT للبيانات والأكوان. الفرق الرئيسي هو أن HoTT يستغني عن البديهية من الأدلة غير الهامة. وهذا يعني أنه لا يوجد من البديهية الخاصة في HoTT التي تفترض أن جميع عناصر البيانات متساوية. ولكن في HoTT ، يعتبر النوع ، بحكم تعريفه ، بيانًا إذا كان يمكن إثبات أن جميع عناصره متساوية مع بعضها البعض. يمكننا تحديد تقدير على أنواع صحيحة إذا كان النوع عبارة:

 \func isProp (A : \Type) => \Pi (aa' : A) -> a = a' 

السؤال الذي يطرح نفسه: ما هي الأنواع التي تفي بهذا المسند ، أي هي البيانات؟ من السهل التحقق من صحة ذلك بالنسبة للأنواع الفارغة والمفردة. بالنسبة للأنواع التي يوجد بها عنصرين مختلفين على الأقل ، لن يكون هذا صحيحًا بعد الآن.

بالطبع ، نريد تحديد جميع الروابط المنطقية اللازمة عبر البيانات. في القسم 1.1 ، ناقشنا بالفعل كيف يمكن تحديدها باستخدام التركيبات النظرية للكتابة. ومع ذلك ، هناك المشكلة التالية: ليست كل العمليات التي isProp تحتفظ isProp . تحتفظ المنشآت الخاصة بمنتج الأنواع والنوع الوظيفي (التابع) بهذه الخاصية ، بينما لا تحتفظ تركيبات مجموع الأنواع والأزواج التابعة. وبالتالي ، لا يمكننا استخدام الخلل وقياس الوجود.

يمكن حل هذه المشكلة بمساعدة بناء جديد ، يتم إضافته إلى HoTT ، ما يسمى باقتراح الاقتراح . يسمح لك هذا التصميم بتحويل أي نوع إلى بيان. يمكن اعتباره عملية رسمية ، مما يجعل جميع المصطلحات التي تسكن هذا النوع متساوية. تشبه هذه العملية إلى حد ما التعليقات التوضيحية لعدم الأهمية من Agda ، ومع ذلك ، فهي ، على عكسها ، عملية كاملة على الأنواع ذات التوقيع \Type -> \Prop .

المثال الأخير الهام للبيانات هو المساواة بين عنصرين من نوع ما. اتضح أنه في الحالة العامة a = a' لا يجب أن يكون نوع المساواة a = a' عبارة. تسمى الأنواع التي هي واحدة مجموعات:

 \func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a') 

جميع الأنواع التي توجد في لغات البرمجة العادية تفي بهذا المسند ، أي أن المساواة بينهم هي بيان. على سبيل المثال ، ينطبق هذا على الأرقام الطبيعية والأعداد الصحيحة ومنتجات المجموعات ومجموعات المجموعات والوظائف على المجموعات وقوائم المجموعات وأنواع البيانات الاستقرائية الأخرى التي تم إنشاؤها من مجموعات. هذا يعني أننا إذا كنا مهتمين فقط بهذه الإنشاءات المألوفة ، فلا يمكننا التفكير في الأنواع التعسفية التي لا تفي بهذا المسند. جميع الأنواع الموجودة في كوك هي مجموعات .

تصبح الأنواع غير المحددة مفيدة إذا كنت تريد التعامل مع نظرية نوع homotopy. في الوقت الحالي ، نقوم ببساطة بإحالة القارئ إلى الوحدة النمطية للمكتبة القياسية التي تحتوي على تعريف المجال البعد n ، مثال على نوع ليس مجموعة.

يحتوي Arend على أكوان خاصة \Prop و \Set ، تتكون من بيانات ومجموعات ، على التوالي. إذا علمنا بالفعل أن النوع A موجود في الكون \Prop (أو \Set ) ، فيمكن الحصول على دليل isProp (أو isSet ) isSet في Arend باستخدام Path.inProp axiom المضمنة في المقدمة (نعطي مثالًا على استخدام هذه البديهية في القسم 2.3).

 \func inProp {A : \Prop} : \Pi (aa' : A) -> a = a' 

لقد لاحظنا بالفعل أنه ليس كل التركيبات الطبيعية على الأنواع تحتفظ isProp . على سبيل المثال ، أنواع البيانات الاستقرائية مع اثنين أو أكثر من المنشئات لا ترضيها. كما هو مذكور أعلاه ، يمكننا استخدام بنية الاقتطاع المقترحة التي تحول أي نوع إلى بيان.
في مكتبة Arend ، يُطلق على التطبيق القياسي للاقتراح Logic.TruncP . يمكننا تحديد نوع من المنطقية "أو" في Arend على أنه اقتطاع مجموع الأنواع:

 \data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/" 

في Arend ، هناك طريقة أخرى أبسط وأكثر ملاءمة لتحديد نوع حثي مقطوع بشكل مقترح. للقيام بذلك ، ما عليك سوى إضافة الكلمة الرئيسية \truncated قبل تحديد نوع البيانات. على سبيل المثال ، يتم تقديم تعريف المنطقي "أو" في مكتبة Arend القياسية على النحو التالي.

 \truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B 

يشبه العمل الإضافي مع الأنواع المقطوعة بشكل مقترح ، الأنواع التي تم تعيينها Prop في Coq. على سبيل المثال ، يُسمح بمطابقة النقش لمتغير يكون نوعه عبارة فقط في موقف يكون فيه نوع التعبير الذي يتم تعريفه عبارة عن عبارة. وبالتالي ، من السهل دائمًا تحديد الوظيفة Or-to-|| من خلال المقارنة مع العينة ، ولكن الوظيفة العكسية لها ، فقط إذا كان النوع A `Or` B عبارة (وهو أمر نادر بما فيه الكفاية ، على سبيل المثال ، عندما يكون النوعان A و B عبارة عن عبارات `Or` كل منهما الآخر).

 \func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight 

أذكر أيضًا أن خصوصية آلية الأكوان في Coq هي أنه إذا تم تخصيص بعض التعريفات لكون Prop ، فلن يكون من الممكن بأي حال من الأحوال استخدامه في الحساب. لهذا السبب ، لا ينصح مطورو Coq أنفسهم باستخدام الإنشاءات المقترحة ، ولكن ينصحون باستبدالها بنظائر من عالم المجموعات إن أمكن. لا تحتوي آلية أكوان Arend على هذا العيب ، أي أنه في بعض المواقف يمكن استخدام البيانات في العمليات الحسابية. سنقدم مثالاً على مثل هذا الموقف عندما نناقش تنفيذ خوارزمية فرز القائمة.

1.4 فصول في أرند

نظرًا لأن هدفنا هو تطبيق أبسط خوارزميات الفرز ، يبدو أنه من المفيد أن تتعرف على تنفيذ المجموعات المرتبة المتوفرة في مكتبة Arend القياسية.

في Arend ، يتم استخدام الفئات لتضمين العمليات والبديهيات التي تحدد الهياكل الرياضية ، وكذلك لتسليط الضوء على العلاقات بين هذه الهياكل باستخدام الوراثة. الفصول هي أيضا مساحات أسماء ، والتي من المناسب أن تضع الإنشاءات والنظريات المناسبة في المعنى.

الفئة الأساسية التي يتم من خلالها توريث جميع فئات الترتيب في Arend هي فئة BaseSet ، والتي لا تحتوي على أي أعضاء بخلاف التعيين E لمجموعة المضيف (على سبيل المثال ، المجموعة التي BaseSet المنحدرة من BaseSet بالفعل بتقديم عمليات متنوعة). النظر في تعريف هذه الفئة من مكتبة Arend القياسية.

 \class BaseSet (E : \Set) -- ,     

في التعريف أعلاه ، يُعلن عن الموجة الحاملة E معلمة صنف. قد يتساءل المرء ، هل هناك اختلاف في التعريف أعلاه لـ BaseSet عن التعريف التالي ، في أي ناقل E يتم تعريفه كحقل فئة؟

 \class BaseSet' --      | E : \Set 

الجواب غير متوقع قليلاً هو أنه في Arend لا يوجد فرق بين التعريفين ، بمعنى أن أي معلمة فئة (حتى ضمنية) في Arend هي ، في الواقع ، مجالها. وبالتالي ، بالنسبة لكل من BaseSet ، يمكن للمرء استخدام التعبير xE للوصول إلى الحقل E. BaseSet يزال هناك فرق بين المتغيرات المذكورة أعلاه لتعريف BaseSet ، لكن الأمر أكثر دقة ، وسوف ندرسه بمزيد من التفاصيل في القسم التالي عندما نناقش مثيلات الفصل الدراسي ( حالات الطبقة).

لا يكون تشغيل فرز قائمة منطقيًا إلا إذا تم تحديد ترتيب خطي على نوع الكائنات في القائمة ، وبالتالي ، فإننا نأخذ بعين الاعتبار تعاريف مجموعة صارمة مرتبة جزئيًا ومجموعة محددة ترتيبًا خطيًا.

 \class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y } 

من وجهة نظر نظرية النوع ، يمكن اعتبار الفئات في Arend نظائرها لأنواع سيغما مع بناء جملة أكثر ملاءمة للتوقعات والمنشئين. , Arend- -, .

, . , . , StrictPoset <-irreflexive <-transitive , E < — . , (, , ) , .

, , . , Arend , , . , . , , , , . :

 \class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y) 

Dec , Dec E , E , E , E .

 \data Dec (E : \Prop) | yes E | no (Not E) 

أخيرًا ، ضع في الاعتبار الفصل Dec(من الكلمة decidable) من الوحدة النمطية Order.LinearOrder. تطبق الفئة ديسمبر أوامر خطية قابلة للحل ، وعلى وجه الخصوص ، تحتوي على البديهية التي نحتاجها trichotomy، مما يعني أن أي عنصرين من النوع Eقابلان للمقارنة فيما يتعلق بالترتيب <. وبالتالي ، Decيمكن اعتباره بمثابة تماثل للواجهة المقارنة من Java.

 \class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} --   | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} } 

Dec Dec , , , , . Dec , .

, Dec ( ). Dec , Arend ( Dec LinearOrder, DecSet ), , (diamond inheritance).

: , ( , ).

Dec Order.LinearOrder IDEA ( [Ctrl]+[H]), , .



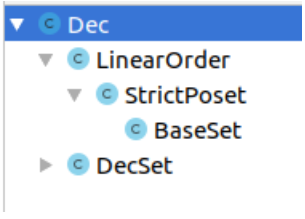
Arend ( IDEA BaseSet ). , .

1.5 , , .

StrictPoset Nat. Arend , . -, , , - ( ), .

: . .

 data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z') 

\func \lemma . , , , . , \lemma , \Prop .

x'<y' — -, x' < y' . - (.. , , ).

(instance) StrictPoset. يحتوي Arend على العديد من خيارات بناء الجملة المختلفة لهذا الغرض. الطريقة الأولى لإنشاء مثيل لفصل دراسي هي استخدام كلمة أساسية \newداخل أي تعبير. في هذه الحالة ، سيتم إنشاء "مثيل فئة مجهولة".

 \func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

StrictPoset { … } \new : - StrictPoset . - , , , \new . \new C { … } C { … } . C, C. , , NatOrder StrictPoset .

, . , StrictPoset Nat StrictPoset { | E => Nat } . , NatOrder StrictPoset , ( ).

NatOrder \cowith ( - ).

 \func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

, , \instance.

 \instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

Arend , Haskell. NatOrder \instance \cowith , StrictPoset ( ).

, BaseSet - E ( ), , E . .

, Arend . Arend , , ( , « » \classifying \field , Arend ). :

• Arend . , X StrictPoset , List X List XE .
  
• Arend .

, . , \instance StrictPoset , Nat Int ( NatOrder IntOrder ).

, x < y , x, y , , x, y . Arend , NatOrder.< , — IntOrder.< .

, . Arend , < StrictPoset , E. , Arend x<y StrictPoset ( ), E . , < .

, Arend. , \use \coerce . Arend - بعض مساحة الاسم المستخدمة لوضع مختلف الهياكل المساعدة في ذلك. لإضافة أي تعريفات أخرى إلى وحدة التعريف المرتبطة ، يتم استخدام الكلمة الأساسية \where.

النظر في أبسط مثال على استخدام آلية تحويل النوع. fromNatسيتم استخدام الدالة لتحويل الأرقام الطبيعية ضمنيًا إلى أعداد صحيحة.

 \data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n } 

\use \coerce \func , . , , (, , ).

: HoTT JetBrains Research.