صادفت لغزًا مثيرًا للاهتمام: في الحقيقة ، يتم إعطاء الرقم a والأعداد الصحيحة الموجبة n. حساب الجذر رقم من دون استخدام المكتبات.
بيانات الإدخال: الرقم a حقيقي ، غير سالب ، لا يتجاوز 1000 ، تم تحديده بدقة 6 منازل عشرية. الرقم n طبيعي ، ولا يتجاوز 10.
الإخراج: يجب على البرنامج إخراج رقم واحد: الإجابة على المشكلة بدقة لا تقل عن 5 منازل عشرية.
بطبيعة الحال ، كان من المثير للاهتمام حلها في مسودة بقلم رصاص ، ثم رسمها في المحرر ومحاولة تجميعها. دون googling ، نصائح وحتى أكثر من ذلك باستخدام المكتبات. إذا قررت ذلك للمرة الأولى ، فحاول أولاً كتابة برنامج للعثور على الجذر التربيعي المعتاد. إذا وجدت المهمة صعبة ، فقم بحلها تقريبًا ولكن أبسط. ثم سوف يزول خوفك وسيظهر نوع من الفهم القاسي.
بالنسبة للمبتدئين ، سأقدم مثالًا عن كيفية حساب الجذر التربيعي دون استخدام وظيفة مكتبة. خوارزمية التكرار التتابعي. يتقارب بسرعة كبيرة حتى بالنسبة للأعداد الكبيرة.
#include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
يمكنك تشغيل الكود هنا:
انقرتعقيد لوغاريتم الخوارزمية؟ أو آخر؟ :)
يمكنك الآن الانتقال إلى الإصدار المعقد من المهمة. في هذه الحالة ، يكون الحل أكثر تعميماً.
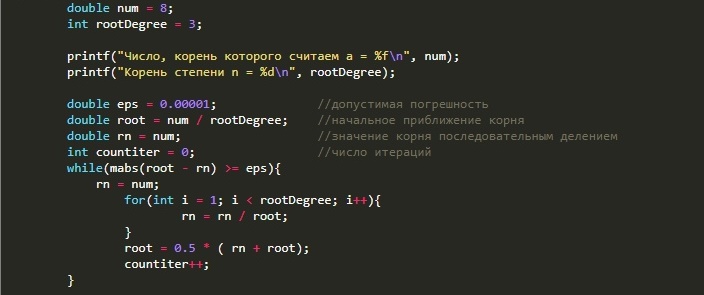
#include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(", = %f\n", num); printf(" n = %d\n", rootDegree); double eps = 0.00001; // double root = num / rootDegree; // double rn = num; // int countiter = 0; // while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf(" = %i\n", countiter); return 0; }
يمكنك تشغيل الكود هنا:
انقرفي هذا الحل ، أستخدم فكرة التقريب الأولي الجيد نسبيًا. ثم التقسيم المتسلسل هو التقريب الثاني لجذر الدرجة التاسعة. بعد ذلك ، يتم اعتبار التقريب الجديد عن طريق حساب المتوسطين الحاليين. على الدوام ، تتقارب الخوارزمية مع الجذر المطلوب مع وجود خطأ محدد مسبقًا. هذا يشبه قليلاً طريقة التكرار.
هذه هي أول خوارزمية تعمل مكتوبة على الركبة. ما زلنا بحاجة إلى التفكير في التعقيدات وإمكانيات التسارع. بالمناسبة ، ما هي ميزات تسريع هذه الخوارزمية التي يمكن تنفيذها في رأيك؟
أشعر أنه سيكون هناك سؤال: "لماذا هذا إذا تم تنفيذ كل شيء في المكتبات قبل مائة عام؟"
الإجابة: شخصياً ، أحببت دائمًا التفكير في الخوارزميات التي يتم تنفيذها بالفعل في المكتبات القياسية. حاول تطويرها بنفسك (جيدًا ، أو لتطوير نوع من المحاكاة الساخرة البطيئة والفشل). إنه يدرب الدماغ جيدًا. لذلك ، في رأيي ، "إعادة اختراع العجلة" مفيد للغاية. ومن الضار بشكل قاطع استخدام كل شيء جاهز دائمًا ، دون أي فكرة عن البنية الداخلية.