يا طريقة هذا نيوتن

لقد كتب الكثير عن طرق التحسين العددية. هذا أمر مفهوم ، خاصة في ظل خلفية النجاحات التي أظهرتها الشبكات العصبية العميقة مؤخرًا. وإنه لمن دواعي السرور البالغ أن بعض المتحمسين على الأقل مهتمون ليس فقط بكيفية قصف شبكتهم العصبية على الأطر التي اكتسبت شعبية في هذه الإنترنت ، ولكن أيضًا كيف يعمل كل ذلك ولماذا. ومع ذلك ، كان لا بد لي من الإشارة إلى أنه في طرح القضايا المتعلقة بتدريب الشبكات العصبية (وليس فقط مع التدريب ، وليس فقط الشبكات) ، بما في ذلك على Habré ، يتم استخدام عدد من العبارات "المعروفة" في كثير من الأحيان لإعادة توجيه ، والتي صلاحية بعبارة ملطفة ، مشكوك فيه. من بين هذه العبارات المشكوك فيها:

1. أساليب الأوامر الثانية والمزيد لا تعمل بشكل جيد في مهام تدريب الشبكات العصبية. لأن ذلك.
2. تتطلب طريقة نيوتن حتمية إيجابية لمصفوفة هسيان (المشتقات الثانية) وبالتالي لا تعمل بشكل جيد.
   
3. تعد طريقة Levenberg-Marquardt حلاً وسطًا بين نزول التدرج وطريقة نيوتن وهي بشكل عام مجريات الأمور.
   

إلخ بدلاً من الاستمرار في هذه القائمة ، من الأفضل الدخول إلى العمل. في هذا المنشور سننظر في البيان الثاني ، حيث قابلته مرتين على الأقل في حبري. سأتطرق إلى السؤال الأول فقط في الجزء المتعلق بطريقة نيوتن ، لأنه أكثر شمولاً. سيتم ترك الثالث والباقي حتى أوقات أفضل.

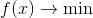
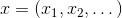
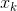
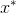
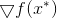
سيكون تركيز اهتمامنا على مهمة التحسين غير المشروط حيث - نقطة مساحة المتجه ، أو ببساطة - متجه. بطبيعة الحال ، هذه المهمة أسهل في الحل ، وكلما علمنا عنها . يفترض عادةً أن يكون مختلفًا فيما يتعلق بكل حجة ، ومرات عديدة كما هو مطلوب لأفعالنا القذرة. ومن المعروف أن هناك شرطا ضروريا لذلك في وقت ما يتم الوصول إلى الحد الأدنى ، هو المساواة في التدرج في الوظيفة عند هذه النقطة الصفر. من هنا نحصل على الفور على طريقة التقليل التالية:

حل المعادلة .

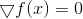
المهمة ، بعبارة ملطفة ، ليست مهمة سهلة. بالتأكيد ليس أسهل من الأصل. ومع ذلك ، في هذه المرحلة ، يمكننا أن نلاحظ على الفور العلاقة بين مشكلة التصغير ومشكلة حل نظام المعادلات غير الخطية. سيعود هذا الاتصال إلينا عند التفكير في طريقة Levenberg-Marquardt (عندما نصل إليها). في غضون ذلك ، تذكر (أو اكتشف) أن إحدى الطرق الأكثر شيوعًا لحل أنظمة المعادلات غير الخطية هي طريقة نيوتن. يتكون في حقيقة أن حل المعادلة نحن نبدأ من بعض التقريب الأولي بناء تسلسل

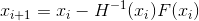
- طريقة نيوتن الصريحة

أو

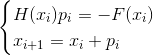
- طريقة نيوتن الضمنية

حيث - مصفوفة مكونة من مشتقات جزئية للدالة . بطبيعة الحال ، في الحالة العامة ، عندما يتم إعطاء نظام المعادلات غير الخطية لنا ببساطة في الأحاسيس ، يتطلب شيئًا ما من المصفوفة نحن لسنا مؤهلين. في الحالة التي تكون فيها المعادلة هي شرط الحد الأدنى لبعض الوظائف ، يمكننا أن نذكر أن المصفوفة متماثل. لكن ليس أكثر.

تمت دراسة طريقة نيوتن لحل أنظمة المعادلات غير الخطية جيدًا. وها هو الشيء - بالنسبة لتقاربها ، لا يلزم الدقة الإيجابية للمصفوفة . نعم ، ولا يمكن أن يكون مطلوبًا - وإلا فقد كان بلا قيمة. بدلاً من ذلك ، هناك شروط أخرى تضمن التقارب المحلي لهذه الطريقة والتي لن نأخذها بعين الاعتبار هنا ، وإرسال الأشخاص المهتمين إلى الأدبيات المتخصصة (أو في تعليق). لقد حصلنا على أن العبارة 2 خاطئة.

إلى هذا الحد؟

نعم ولا. الكمين هنا في الكلمة هو التقارب المحلي قبل الكلمة. وهذا يعني أن التقريب الأولي يجب أن تكون "قريبة بما فيه الكفاية" من الحل ، وإلا في كل خطوة سنكون أبعد وأكثر إزالتها منه. ماذا تفعل؟ لن أخوض في تفاصيل كيفية حل هذه المشكلة لأنظمة المعادلات غير الخطية ذات الشكل العام. بدلاً من ذلك ، عد إلى مهمة التحسين الخاصة بنا. الخطأ الأول في البيان 2 هو في الواقع أن التحدث عادة عن طريقة نيوتن في مشاكل التحسين ، يعني تعديله - طريقة نيوتن المخففة ، حيث يتم إنشاء تسلسل التقريب وفقًا للقاعدة

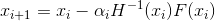
- طريقة نيوتن الواضحة

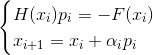
- طريقة نيوتن الضمنية الضمنية

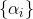
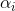
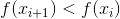
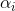
هنا التسلسل هي معلمة الأسلوب وبنائها مهمة منفصلة. في مشاكل التقليل ، طبيعي عند الاختيار سيكون هناك شرط ، في كل تكرار ، تنخفض قيمة الوظيفة f ، أي . يطرح سؤال منطقي: هل هناك مثل هذا (إيجابي) ؟ وإذا كانت الإجابة على هذا السؤال إيجابية ، إذن دعا اتجاه النسب. ثم يمكن طرح السؤال بهذه الطريقة:
متى يكون الاتجاه الناتج عن طريقة نيوتن هو اتجاه النسب؟
وللإجابة عليه ، يجب أن تنظر إلى مشكلة التقليل من جانب آخر.

طرق النزول

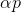
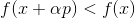
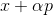
بالنسبة لمشكلة التقليل ، يبدو هذا النهج طبيعيًا: بدءًا من نقطة تعسفية ، نختار الاتجاه p بطريقة أو بأخرى ونخطو خطوة في هذا الاتجاه . إذا ثم خذ كنقطة انطلاق جديدة وكرر الإجراء. إذا تم اختيار الاتجاه بشكل تعسفي ، فإن هذه الطريقة تسمى أحيانًا طريقة المشي العشوائي. من الممكن أن تأخذ المتجهات أساس الوحدة كإتجاه - أي أن تأخذ خطوة في إحداثي واحد فقط ، هذه الطريقة تسمى طريقة إحداثي الإحداثيات. وغني عن القول ، فهي غير فعالة؟ لكي يعمل هذا النهج بشكل جيد ، نحتاج إلى بعض الضمانات الإضافية. للقيام بذلك ، نقدم وظيفة مساعدة . 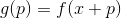أعتقد أنه من الواضح أن التقليل يعادل تماما إلى الحد الأدنى . إذا التفريق بعد ذلك يمكن أن تمثل



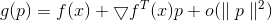
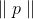
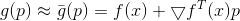
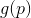
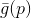
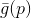
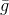
و لو صغيرة بما فيه الكفاية بعد ذلك . يمكننا الآن محاولة استبدال مشكلة التقليل مهمة تقليل تقريبها (أو النموذج ) . بالمناسبة ، جميع الأساليب القائمة على استخدام النموذج دعا التدرج. لكن المشكلة هي ، هي وظيفة خطية ، وبالتالي ، ليس لها حد أدنى. لحل هذه المشكلة ، نضيف قيودًا على طول الخطوة التي نريد اتخاذها. في هذه الحالة ، يعد هذا مطلبًا طبيعيًا تمامًا - لأن نموذجنا يصف الوظيفة الموضوعية بشكل أو بآخر بشكل صحيح فقط في حي صغير بما فيه الكفاية. نتيجة لذلك ، نحصل على مشكلة إضافية تتمثل في التحسين الشرطي:



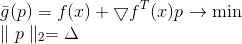
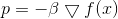
هذه المهمة لديها حل واضح: حيث - عامل يضمن وفاء القيد. ثم تكرارات طريقة النسب تأخذ الشكل

.

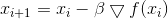
التي نتعلم فيها طريقة النسب التدرج المعروفة. معلمة ، والتي تسمى عادةً سرعة الهبوط ، اكتسبت الآن معنى مفهومًا ، ويتم تحديد قيمتها من خلال الحالة التي تكمن فيها النقطة الجديدة في مجال نصف قطر معين ، مقيد حول النقطة القديمة.

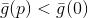
بناءً على خصائص النموذج المبني للوظيفة الموضوعية ، يمكننا القول أن هناك مثل هذا ، حتى لو كانت صغيرة جدا ، ماذا لو ثم . تجدر الإشارة إلى أنه في هذه الحالة ، لا يعتمد الاتجاه الذي سنتحرك فيه على حجم نصف قطر هذا المجال. بعد ذلك يمكننا اختيار إحدى الطرق التالية:

1. حدد وفقًا لبعض الطريقة القيمة .
2. قم بتعيين مهمة اختيار القيمة المناسبة ، وتوفير انخفاض في قيمة وظيفة الهدف.

النهج الأول هو نموذجي لطرق منطقة الثقة ، والثاني يؤدي إلى صياغة مشكلة مساعدة ما يسمى البحث الخطي (LineSearch) . في هذه الحالة بالذات ، تكون الاختلافات بين هذه الأساليب صغيرة ولن نأخذها بعين الاعتبار. بدلاً من ذلك ، انتبه لما يلي:

لماذا ، في الواقع ، نحن نبحث عن تعويض الكذب بالضبط على الكرة؟

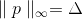
في الواقع ، يمكننا استبدال هذا القيد بشرط ، على سبيل المثال ، أن p ينتمي إلى سطح المكعب ، أي (في هذه الحالة ، ليس من المعقول للغاية ، ولكن لماذا لا) ، أو بعض سطح بيضاوي الشكل؟ هذا يبدو بالفعل منطقيًا تمامًا ، إذا استذكرنا المشكلات التي تنشأ عند تقليل وظائف الإخدار. جوهر المشكلة هو أنه على طول بعض خطوط الإحداثيات ، تتغير الوظيفة بشكل أسرع من غيرها. لهذا السبب ، نحصل على أنه إذا كانت الزيادة يجب أن تنتمي إلى الكرة ، ثم الكمية يجب أن يكون "النسب" فيه صغيرًا جدًا. وهذا يؤدي إلى حقيقة أن تحقيق الحد الأدنى يتطلب عددًا كبيرًا جدًا من الخطوات. لكن إذا أخذنا بدلاً من ذلك قطع ناقص مناسب كجوار ، فإن هذه المشكلة سوف تظهر بلا معنى.

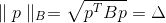
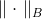
بشرط أن تنتمي نقاط السطح الإهليلجي ، يمكن كتابتها كـ حيث هو بعض مصفوفة محددة إيجابية ، وتسمى أيضا متري. نورما دعا القاعدة الاهليلجيه الناجم عن المصفوفة . ما نوع المصفوفة هذا ومن أين نحصل عليها - سننظر لاحقًا ، والآن نأتي إلى مهمة جديدة.



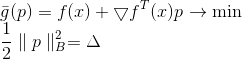
مربع القاعدة والعامل 1/2 هنا فقط للراحة ، حتى لا تعبث بالجذور. عند تطبيق أسلوب لاغرانج المضاعف ، نحصل على مشكلة ملزمة للتحسين غير المشروط



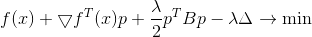
شرط ضروري للحصول على الحد الأدنى لذلك هو

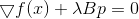
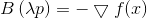
أو من اين







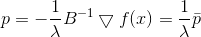
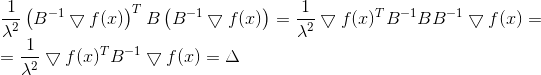
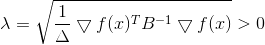
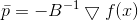
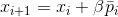
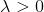
مرة أخرى نرى أن الاتجاه ، التي سنتحرك فيها ، لا تعتمد على القيمة - فقط من المصفوفة . ومرة أخرى ، يمكننا إما التقاط هذا محفوف بالحاجة إلى حساب وانعكاس المصفوفة الصريحة أو حل المشكلة المساعدة لإيجاد تحيز مناسب . كما ، ويضمن الحل لهذه المشكلة المساعدة في الوجود.

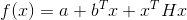
فماذا يجب أن يكون للمصفوفة B؟ نحن نقتصر على الأفكار المضاربة. إذا كانت الوظيفة الهدف - من الدرجة الثانية ، وهذا هو ، لديه الشكل حيث واضح إيجابي ، فمن الواضح أن أفضل مرشح لدور المصفوفة هو هسي ، لأنه في هذه الحالة ، يلزم تكرار طريقة النسب التي أنشأناها. إذا لم تكن H موجبة ، فلن تكون متريًا ، والتكرارات التي تم إنشاؤها باستخدامها هي تكرارات لطريقة Newton المخففة ، ولكنها ليست تكرارات لطريقة النسب. أخيرًا ، يمكننا إعطاء إجابة صارمة على

سؤال: هل يجب أن تكون المصفوفة الهسية في طريقة نيوتن محددة بشكل إيجابي؟
الإجابة: لا ، ليس مطلوبًا في طريقة نيوتن القياسية أو المخففة. ولكن إذا تم استيفاء هذا الشرط ، فإن طريقة نيوتن المخففة هي طريقة نزول ولديها خاصية التقارب العالمي ، وليس فقط التقارب المحلي.

كتوضيح ، لنرى كيف تبدو مناطق الثقة عند تقليل وظيفة Rosenbrock المعروفة باستخدام النسب المتدرجة وأساليب نيوتن ، وكيف يؤثر شكل المناطق على تقارب العملية.



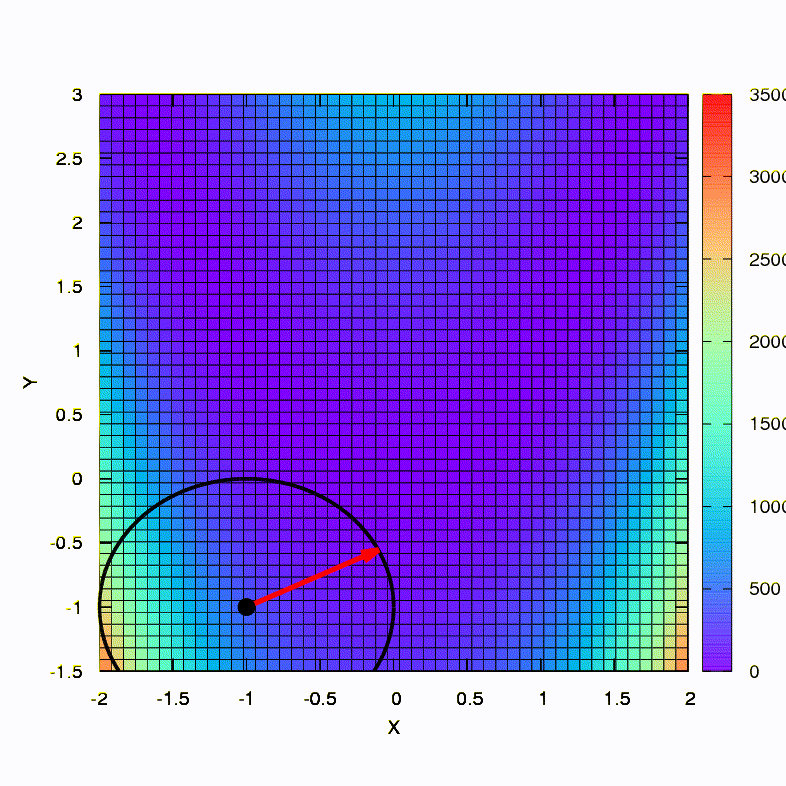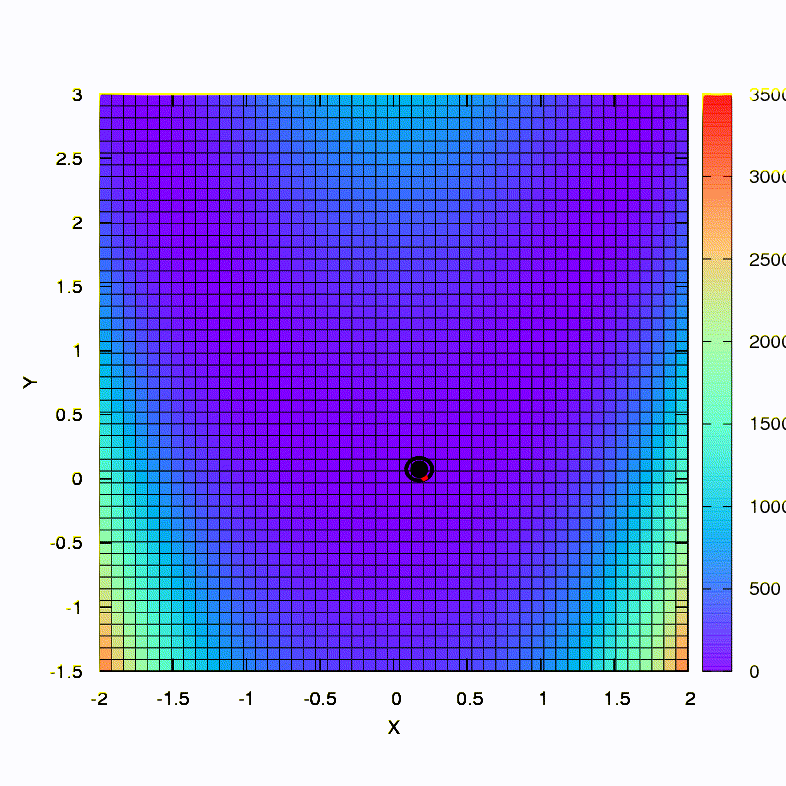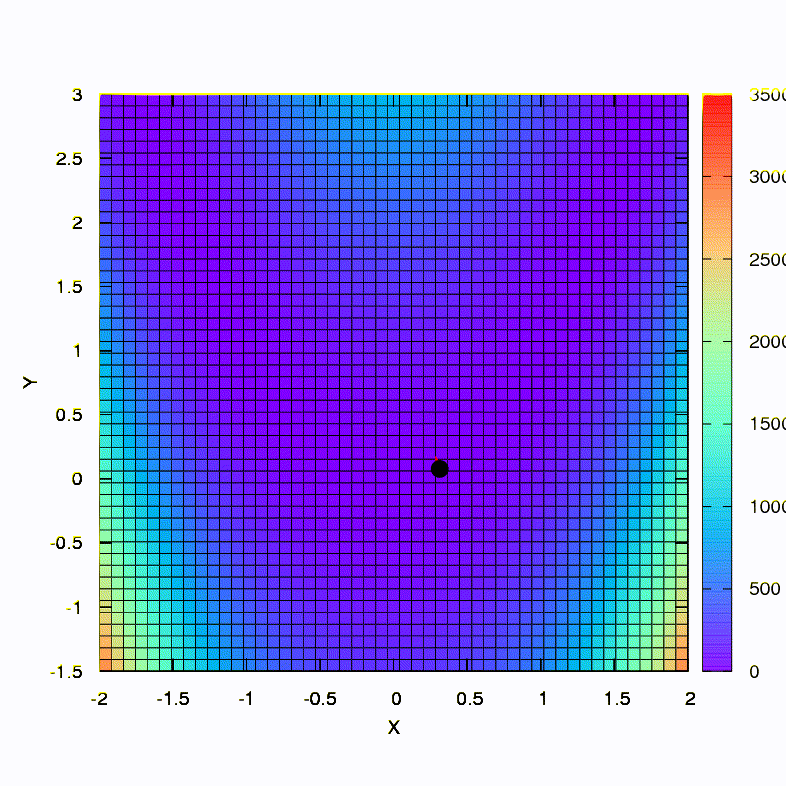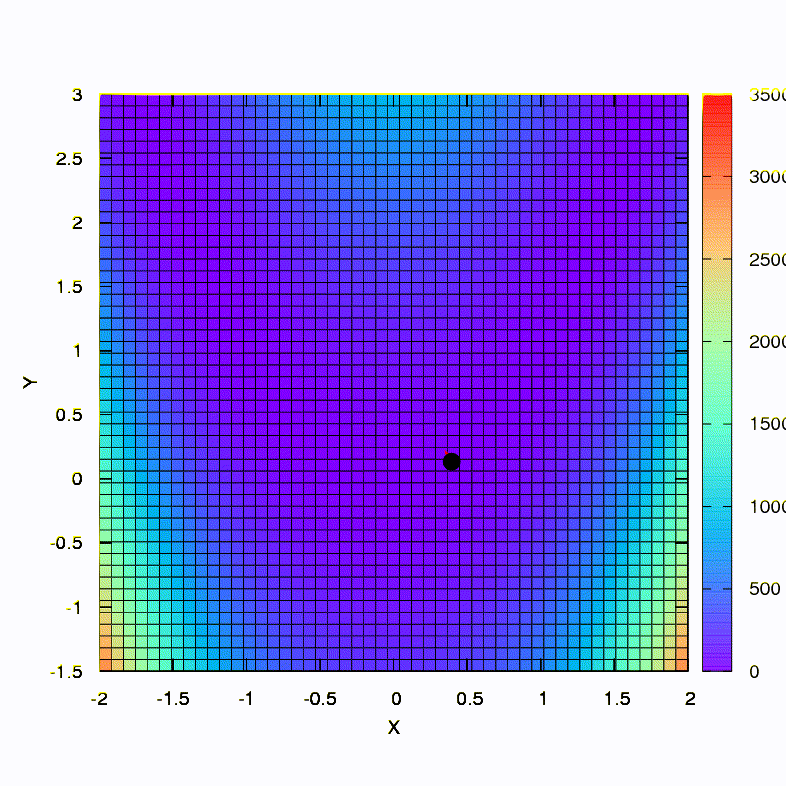
هذه هي الطريقة التي يتصرف بها أسلوب النسب مع منطقة ثقة كروية ، كما أنه منحدر متدرج. كل شيء يشبه الكتاب المدرسي - نحن عالقون في الوادي.



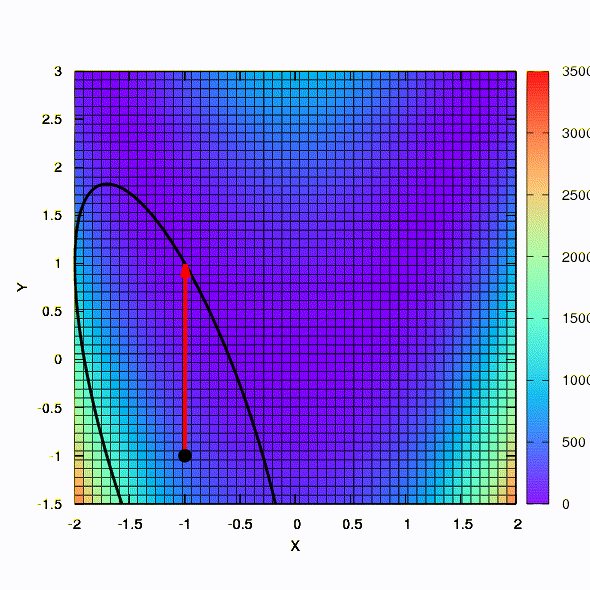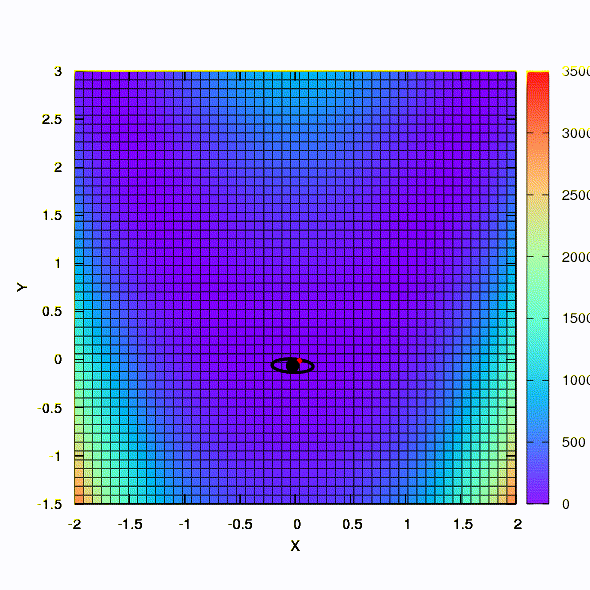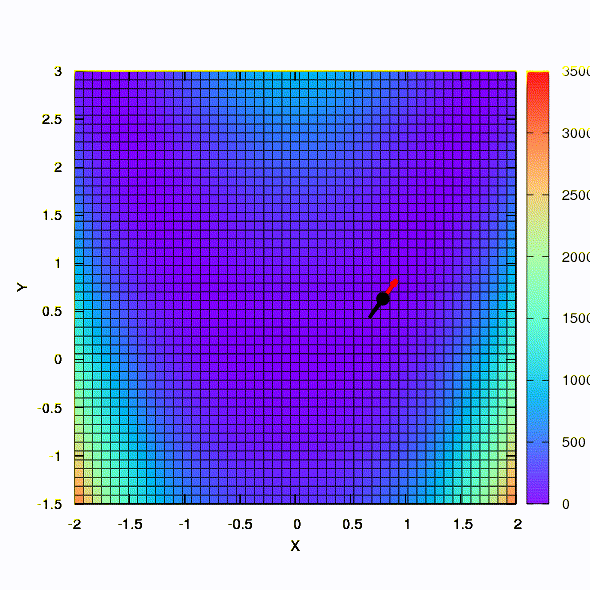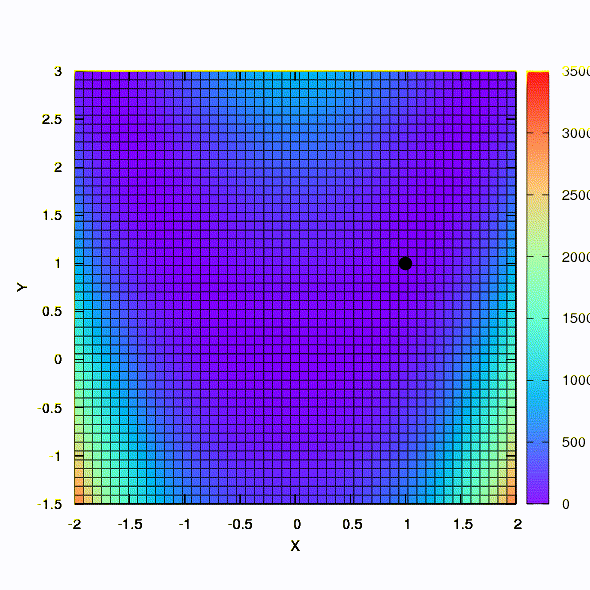
وهذا ما نحصل عليه إذا كانت منطقة الثقة لها شكل القطع الناقص المحدد في مصفوفة هسي. هذا ليس أكثر من تكرار لطريقة نيوتن المثبطة.

فقط مسألة ما يجب القيام به إذا لم تكن مصفوفة هسه إيجابية محددة تبقى دون حل. هناك العديد من الخيارات. الأول هو أن يسجل. ربما تكون محظوظًا وسوف تتلاقى تكرارات نيوتن بدون هذه الخاصية. هذا حقيقي تمامًا ، خاصةً في المراحل الأخيرة من عملية التقليل إلى الحد الأدنى ، عندما تكون قريبًا بالفعل من الحل. في هذه الحالة ، يمكن استخدام تكرارات طريقة نيوتن القياسية دون عناء مع البحث عن حي مقبول للنزول. أو استخدم تكرارات طريقة نيوتن المثبطة في حالة ، في الحالة التي يكون فيها الاتجاه الذي تم الحصول عليه ليس هو اتجاه الهبوط ، قم بتغييره ، على سبيل المثال ، إلى مقاومة الانحدار. فقط لا يجب أن تحقق صراحة ما إذا كان هسي هو إيجابي واضح وفقا لمعيار سيلفستر ، كما حدث هنا !!! . إنه تبذير ولا معنى له.
تتضمن الأساليب الأكثر دقة إنشاء مصفوفة ، بمعنى قريب من المصفوفة Hessian ، ولكن امتلاك خاصية التحديد الإيجابي ، على وجه الخصوص ، عن طريق تصحيح القيم الذاتية. الموضوع المنفصل هو الطرق شبه النيوتونية ، أو الطرق المترية المتغيرة ، والتي تضمن الدقة الإيجابية للمصفوفة B ولا تتطلب حساب المشتقات الثانية. بشكل عام ، تتجاوز المناقشة التفصيلية لهذه المشكلات نطاق هذا المقال.

نعم ، وبالمناسبة ، يستنتج مما سبق أن طريقة نيوتن المثبطة مع الدقة الإيجابية للهيزي هي طريقة متدرجة . وكذلك الطرق شبه النيوتونية. وغيرها الكثير ، بناءً على اختيار منفصل للاتجاه وحجم الخطوة. لذا فإن التباين بين طريقة نيوتن ومصطلحات التدرج غير صحيح.

لتلخيص

طريقة نيوتن ، التي غالباً ما يتم تذكرها عند مناقشة طرق التصغير ، ليست عادةً طريقة نيوتن بمعناها الكلاسيكي ، ولكنها طريقة النزول مع المقياس المحدد بواسطة هيسيان للدالة الموضوعية. ونعم ، يتقارب عالمياً إذا كان الهسيون إيجابيين في كل مكان. هذا ممكن فقط للوظائف المحدبة ، والتي تكون أقل شيوعًا في الممارسة العملية مما نود ، لذلك في الحالة العامة ، دون إجراء التعديلات المناسبة ، فإن تطبيق طريقة نيوتن (لن ننفصل عن الجماعية ونواصل تسميتها) لا يضمن النتيجة الصحيحة. تعلم الشبكات العصبية ، حتى الشبكات الضحلة ، يؤدي عادة إلى مشاكل غير محدبة في الحد الأدنى مع العديد من الحدود الدنيا المحلية. وهنا كمين جديد. عادة ما تتقارب طريقة نيوتن (إذا كانت تتقارب) بسرعة. أقصد سريع جدا. وهذا أمر غريب بشكل سيئ ، لأننا وصلنا إلى الحد الأدنى المحلي في العديد من التكرارات. وقد تكون الوظائف ذات التضاريس المعقدة أسوأ بكثير من الوظائف العالمية. تتقارب نسب التدرج اللوني مع البحث الخطي بشكل أبطأ بكثير ، لكن من المرجح أن "تتخطى" تلال الوظيفة الهدف ، وهو أمر مهم للغاية في المراحل المبكرة من التقليل. إذا كنت قد قللت بالفعل من قيمة الوظيفة الموضوعية ، وتباطأ تقارب النسب المتدرج بشكل كبير ، فقد يؤدي أي تغيير في المقياس إلى تسريع العملية ، ولكن هذا في المراحل النهائية.

بالطبع ، هذه الحجة ليست عالمية ، ولا جدال فيها ، وفي بعض الحالات غير صحيحة. وكذلك القول بأن أساليب التدرج تعمل بشكل أفضل في مشاكل التعلم.