خوارزمية ليفنبرغ ماركوارت بسيطة. خوارزمية ليفنبرغ ماركوارت فعالة.
ويقولون عنه إنه في مكان ما بين نزول التدرج وطريقة نيوتن ، مهما كان ذلك. حسنًا ، إنه من النوع الذي تم
تسويته باستخدام طريقة نيوتن وارتباطه بنسل التدرج. ولكن ماذا يعني عندما ينطقون بهذه العبارة العميقة؟ دعونا نحاول التسلل قليلا.
في مقالاته ، الرفيق ليفنبرغ [ك. طريقة لحل بعض المشاكل في المربعات الأخيرة. رابعا. تطبيق ورقة. الرياضيات. 1944. المجلد. 2. ص 164-168.] ، وبعده المواطن ماركوارت [ماركوارت ، دونالد (1963). "خوارزمية لتقدير المربعات الصغرى للمعلمات غير الخطية." مجلة SIAM على الرياضيات التطبيقية. 11 (2): 431-441.] تعتبر مشكلة المربعات الصغرى ، والتي تبدو كما يلي:

.
والتي يمكن كتابتها أسهل في شكل ناقل

.
ويمكنك حتى أسهل من خلال التسجيل الكامل على المربعات الصغرى. هذا لن يؤثر على القصة.
لذلك ، تعتبر المشكلة

.
تنشأ مثل هذه المشكلة في كثير من الأحيان بحيث لا يمكن المبالغة في أهمية إيجاد طريقة فعالة لحلها. ولكن سنبدأ من آخر. في مقال سابق ، تبين أنه يمكن الحصول على طريقة تدرج النسب المعروفة ، وليس فقط ، من الاعتبارات التالية. دعنا نقول أننا وصلنا إلى مرحلة ما

الذي يهم وظيفة الحد الأدنى

. نحدد وظيفة مساعدة في هذه المرحلة
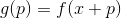
، وكذلك بعض من نموذجها
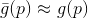
. بالنسبة لهذا النموذج ، نطرح مشكلة مساعدة

حيث

- مجموعة معينة محددة سلفًا من القيم المسموح بها ، يتم اختيارها بحيث يكون للمشكلة حل بسيط ووظيفة
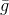
تقريب بدقة تماما

في

. يسمى هذا المخطط طريقة منطقة الثقة ، والكثير

حيث يتم تقليل قيمة وظيفة النموذج - منطقة الثقة لهذه الوظيفة. لنسب التدرج ، اتخذنا

، لطريقة نيوتن

، وكنموذج ل

الجزء الخطي من التوسع تايلور
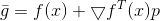
.
دعونا نرى ما يحدث إذا قمنا بتعقيد النموذج من خلال اتخاذ
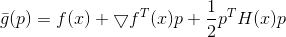
.
نحن تقليل هذه الوظيفة النموذجية في منطقة الثقة الاهليلجيه

(تم إضافة المضاعف لسهولة الحساب). عند تطبيق طريقة لاغرانج المضاعفة ، نحصل على المشكلة

.
الذي حل يرضي المساواة

أو

هنا ، على عكس ما رأيناه سابقًا عند استخدام النموذج الخطي ،
لا يعتمد الاتجاه
p فقط على المقياس 
، ولكن أيضا على اختيار
حجم المنطقة الثقة 
، مما يعني أن تقنية البحث الخطي غير قابلة للتطبيق (على الأقل بشكل معقول). كما تبين أنه من الصعب تحديد القيمة بشكل صريح

المقابلة ل

. ومع ذلك ، فمن الواضح أنه مع زيادة

طول

سوف تنخفض. إذا ، ومع ذلك ، ما زلنا فرض الشرط
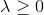
، لن يكون طول الخطوة أكثر من ذلك الذي ستعطيه طريقة نيوتن (كل ما هو عصري ، بدون تعديلات وشروط).
لذلك يمكننا بدلا من ذلك عن معين

ابحث عن القيمة الصحيحة

، افعل العكس تماما: ابحث عن هذا
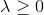
تحت أي شرط

. هذا هو نوع من استبدال البحث المتأخر في هذه الحالة. اقترح ماركوارد الإجراء البسيط التالي:
- إذا لبعض القيمة
 حالة
حالة 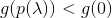 القيام به ثم كرر
القيام به ثم كرر  حتى ل
حتى ل 
- إذا
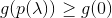 اقبل
اقبل 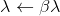 وكرر.
وكرر.
هنا

و

هي الثوابت التي هي معلمات الطريقة. الضرب بواسطة

يتوافق مع توسيع منطقة الثقة ، والضرب في

- تضييق لها.
يمكن تطبيق التقنية المحددة على
أي وظيفة موضوعية. لاحظ أنه لم تعد هناك حاجة إلى التحديد الإيجابي لهيسيان ، على عكس الحالة التي تم بحثها سابقًا ، عندما تم تقديم طريقة نيوتن كحالة خاصة لطريقة النسب المتسلسل. ليست هناك حاجة إلى عدم تنكسها ، وهو أمر مهم للغاية في بعض الحالات. ومع ذلك ، في هذه الحالة ، يرتفع سعر البحث عن الاتجاه ، لأن كل تغيير

يؤدي إلى الحاجة إلى حل نظام خطي لتحديد

.
دعونا نرى ما يحدث إذا طبقنا هذا النهج على مشكلة المربعات الصغرى.
وظيفة التدرج
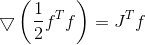
لها هسي
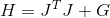
حيث

. استبدل واحصل على النظام التالي الذي يحدد اتجاه البحث
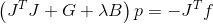
.
هذا أمر مقبول تمامًا ، لكن حساب المشتقات الثانية لدالة المتجه يمكن أن يكون مكلفًا للغاية. اقترح ماركوارت استخدام الوظيفة نفسها لتجاوز هذه المشكلة.

، وتقريبه الخطي
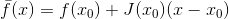
التي المصفوفة

يتحول إلى الصفر. إذا الآن كما

خذ مصفوفة الهوية
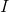
، ثم نحصل على النموذج القياسي لطريقة Levenberg-Marquardt لحل مشكلة المربعات الصغرى:

.
لهذه الطريقة لتحديد اتجاه النزول ، أثبت ماركواردت النظرية التي تطلع

لاتجاه اللانهاية

يميل إلى مكافحة التدرج. يمكن للقارئ المهتم العثور على دليل صارم في المقال الأساسي ، لكنني آمل أن يصبح هذا البيان نفسه واضحًا تمامًا من منطق هذه الطريقة. إلى حد ما ، فإنه يبرر الإشارة في كل مكان إلى حقيقة أنه مع زيادة لامدا (والتي لسبب ما أسميه في كثير من الأحيان المعلمة التنظيم) نحصل على النسب التدرج. في الواقع ، لا شيء من هذا القبيل - فسنحصل عليه فقط في الحد الأقصى ، حيث يكون طول الخطوة يميل إلى الصفر. الأهم من ذلك أنه مع وجود قيمة كبيرة للغاية بما فيه الكفاية ، سيكون الاتجاه الذي نحصل عليه هو
اتجاه الهبوط ، مما يعني أننا نحصل على
التقارب العالمي لهذه الطريقة . وهنا الجزء الثاني من البيان أنه عندما تميل لامدا إلى الصفر نحصل على طريقة نيوتن ، هذا صحيح بشكل واضح ، لكن فقط إذا قبلنا بدلاً من ذلك

تقريبه الخطي
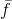
.
يبدو أن كل شيء. نقوم بتقليل قاعدة وظيفة المتجه في القياس الإهليلجي - نستخدم Levenberg-Marquardt. نحن نتعامل مع دالة ذات شكل عام ولدينا القدرة على حساب مصفوفة المشتقات الثانية - بالنسبة للآبار ، استخدم طريقة منطقة ثقة المنطقة العامة. ولكن هناك منحرفين ...
في بعض الأحيان طريقة Levenberg-Marquardt لتقليل الوظيفة

يسمونه تعبير مثل هذا:

.
يبدو أن كل شيء هو نفسه ، ولكن هنا

- مصفوفة الثانية! وظائف مشتقة

. رسميا ، هذا له الحق في الوجود ، لكنه تحريف. وهنا السبب. واقترح نفس ماركوارت في مقاله طريقة لحل نظام المعادلات

عن طريق تقليل الوظيفة

الطريقة الموصوفة. إذا ك
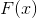
خذ التدرج اللوني للوظيفة الموضوعية ، ثم نحصل حقًا على التعبير المخفض. والانحراف هو بسبب
يتم حل مشكلة التقليل الناتجة عن نظام المعادلات غير الخطية الناتجة عن مشكلة التقليل .
ضربة مزدوجة. مثل هذا التعبير ، على الأقل ، ليس أفضل من المعادلة الأولى لمنطقة الثقة الكروية ، ولكن بشكل عام هو أسوأ بكثير من وجهة نظر الإنتاجية (عمليات الضرب غير الضرورية ، والتطبيقات العادية - التثبيط) ، ومن وجهة نظر استقرار الطريقة (تضاعف المصفوفة في حد ذاته يزداد سوءًا) تكييفها). في بعض الأحيان يعترض على ذلك

مضمون تعريف إيجابي ، ولكن في هذه الحالة لا يهم. دعونا نلقي نظرة على طريقة ليفنبرغ ماركوارت من منظور طريقة النسب المتسلسل. في هذه الحالة ، اتضح أننا نريد استخدام المصفوفة كمقياس
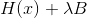
، بحيث يمكنها أن تتصرف بهذه الصفة ، المعنى

يجب التأكد من اليقين الإيجابي. بالنظر إلى ذلك

قيمة محددة إيجابية

يمكن دائما العثور عليها - وبالتالي لا حاجة للطلب من

اليقين الإيجابي لا يلاحظ.
كمصفوفة

ليس من الضروري اتخاذ نموذج واحد ، ولكن بالنسبة للنموذج التربيعي للوظيفة الهدفية ، لم يعد تحديد منطقة ثقة كافية أمرًا بسيطًا تمامًا مثل النموذج الخطي. إذا أخذنا المنطقة الإهليلجية التي يسببها الهسه ، فإن الطريقة تتحول إلى طريقة نيوتن (جيدًا ، تقريبًا)
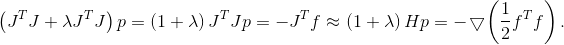
ما لم يكن ، بطبيعة الحال ، مصفوفة هسه محددة إيجابية. إذا لم يكن الأمر كذلك ، فكما كان الحال من قبل ، يمكنك استخدام Hessian المصححة كمقياس ، أو بعض المصفوفات القريبة منه إلى حد ما. هناك أيضًا توصية لاستخدام مصفوفة كمقياس
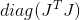
، والتي من خلال البناء ويضمن أن تكون إيجابية محددة. لسوء الحظ ، لا أعرف على الأقل أي مبرر صارم لهذا الخيار ، لكن يتم ذكره في كثير من الأحيان كتوصية عملية.
كتوضيح ، دعونا نرى كيف تتصرف الطريقة على نفس وظيفة Rosenbrock ، وسننظر فيها في شكلين - كدالة بسيطة مكتوبة في النموذج

.
وكمشكلة الأقل الساحات
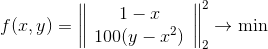

هذه هي الطريقة التي تتصرف بها منطقة الثقة الكروية.
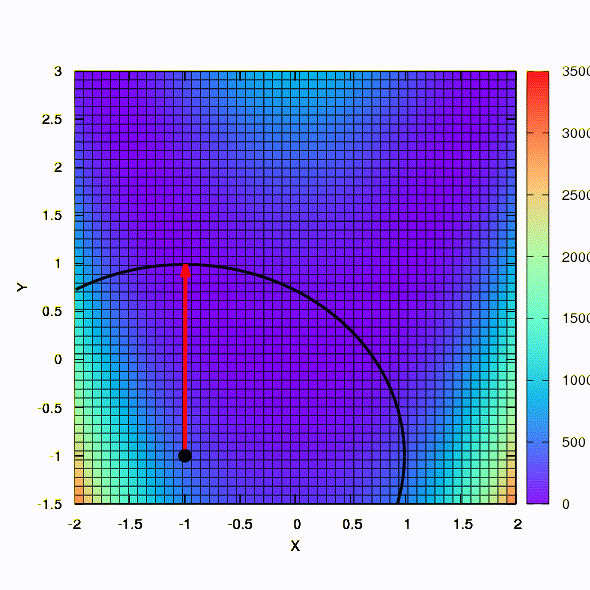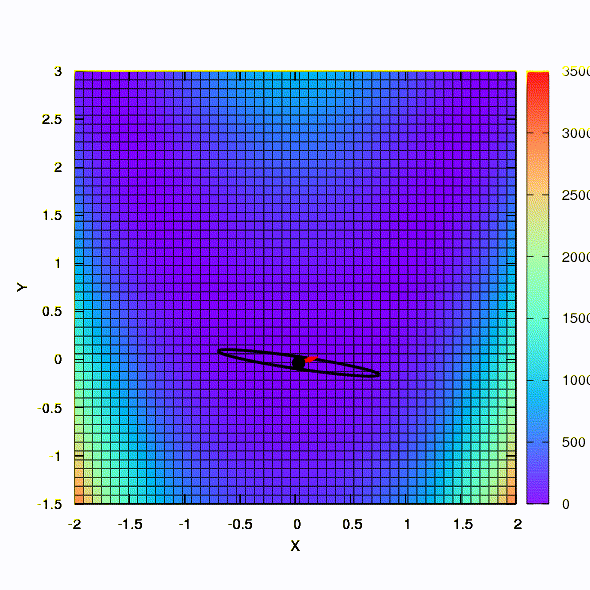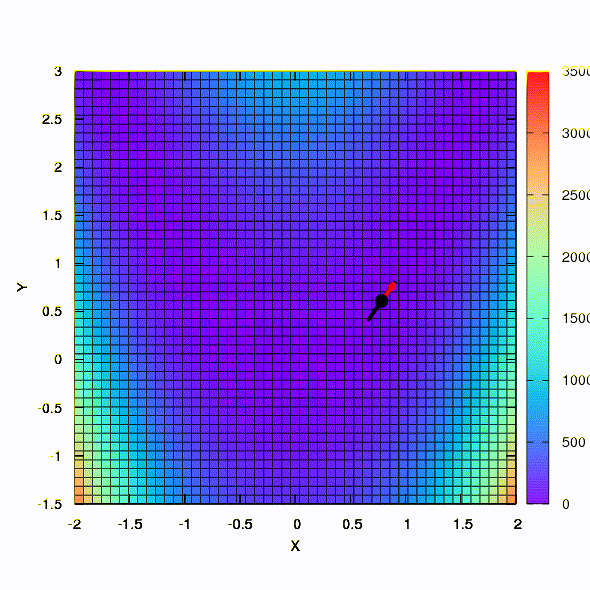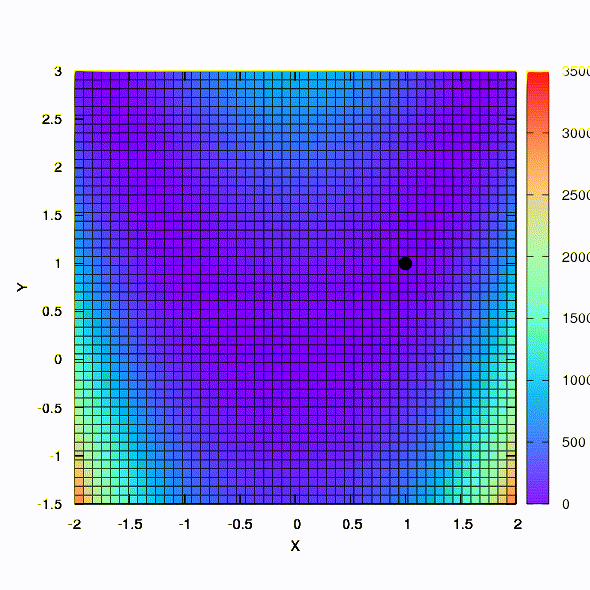
لذلك تتصرف نفس الطريقة إذا تم إعطاء شكل منطقة الثقة بمصفوفة تم إنشاؤها وفقًا لقانون دافيدون فليتشر باول. هناك تأثير على التقارب ، ولكن أكثر تواضعا مما كان عليه في الحالة المماثلة عند استخدام النموذج الخطي للدالة الموضوعية.
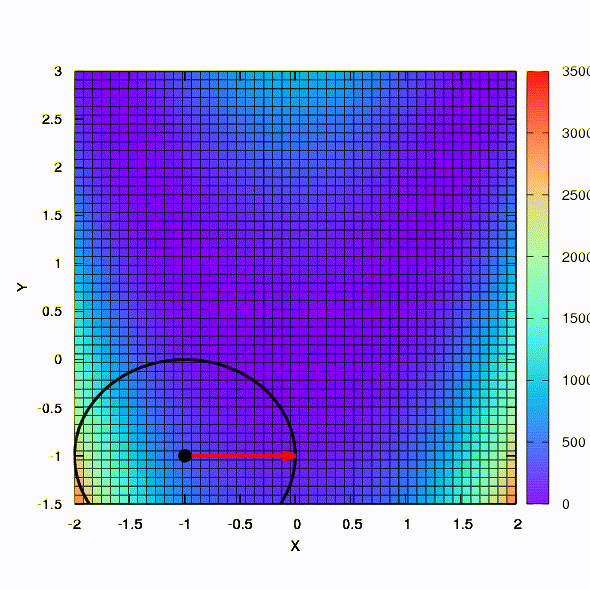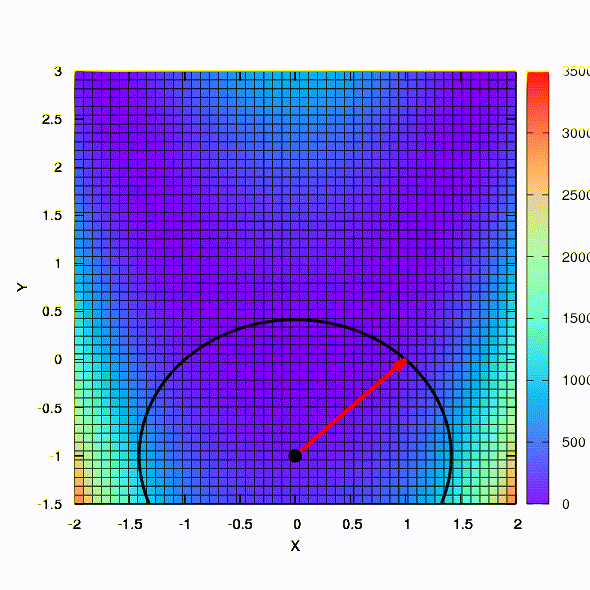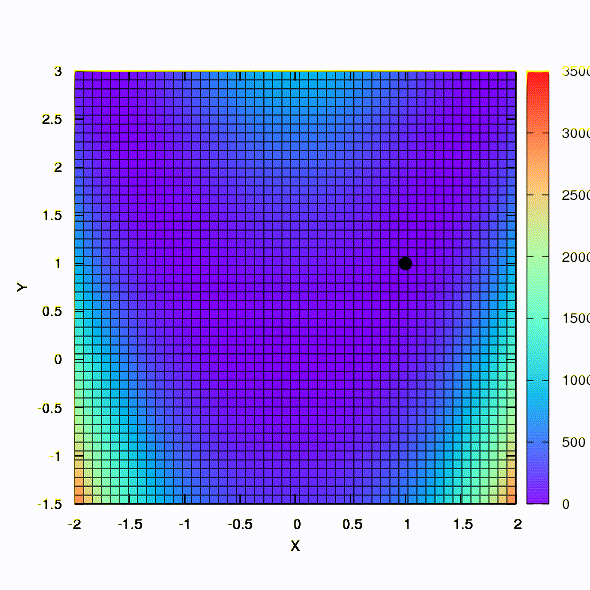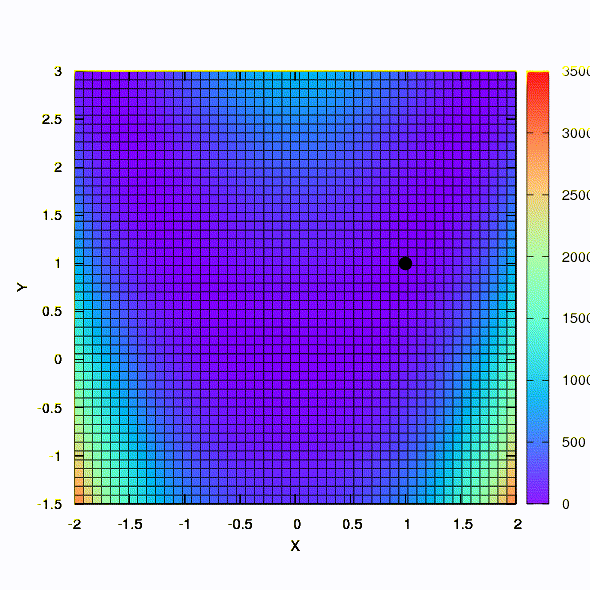
وهذا هو سلوك الأسلوب المطبق على مشكلة المربعات الصغرى. يتقارب في 5 تكرارات. فقط من فضلك ،
لا تستخلص من هذا الاستنتاج أن الصيغة الثانية للوظائف من هذا النوع هي دائما أفضل من الأولى . هذا ليس كذلك ، لقد حدث فقط في هذه الحالة بالذات.
استنتاج
إن طريقة Levenberg-Marquardt هي ، حسب علمي ، الطريقة الأولى القائمة على فكرة منطقة الثقة. لقد أظهر نفسه جيدًا في الممارسة عند حل مشكلة المربعات الصغرى. تتقارب الطريقة في معظم الحالات (التي أراها أنا) بسرعة كبيرة (قلت ما إذا كانت جيدة أو سيئة في مقال سابق). ومع ذلك ، مع تقليل الوظائف العامة إلى الحد الأدنى ، فإنه لا يكاد يكون الخيار الأفضل لاختيار مجال كمنطقة ثقة. بالإضافة إلى ذلك ، هناك عيب كبير في الطريقة (في صيغتها الأساسية ، والتي تم وصفها هنا) هو أن حجم منطقة الثقة تم تحديده ضمنيًا. العيب هو أن معرفة المعنى

يمكننا ، بالطبع ، الاعتماد في الوقت الحالي

مجرد حساب طول الخطوة

. ومع ذلك ، عندما ننتقل إلى نقطة جديدة ، نفس القيمة

قيمة مختلفة تماما من منطقة الثقة تتوافق بالفعل. وبالتالي ، فإننا نفقد القدرة على تحديد حجم "سمة المهمة" لمنطقة الثقة ونضطر إلى تحديد حجمها بطريقة جديدة في كل نقطة جديدة. قد يكون هذا مهمًا عندما يكون هناك عدد كبير بما فيه الكفاية من التكرار مطلوبًا للتقارب ، ويكون حساب قيمة دالة مكلفًا. يتم حل مشكلات مماثلة بطرق أكثر تقدمًا استنادًا إلى فكرة منطقة الثقة.
لكن هذه قصة مختلفة تماما.
إضافة
بفضل التعليقات القيمة لـ
Dark_Daiver ، قررت إضافة ما ذكر أعلاه إلى الملاحظة التالية. بالطبع ، يمكن للمرء أن يصل إلى طريقة ليفنبرغ ماركوارت بطريقة مختلفة تجريبية بحتة. وهي ، دعونا نعود إلى مخطط أسلوب النسب المتسلسل الموضح في المقالة السابقة ونطرح مرة أخرى على أنفسنا مسألة بناء مقياس مناسب للنموذج الخطي للدالة الهدفية.
لنفترض أن مصفوفة Hessian في النقطة الحالية في مساحة البحث ليست محددة بشكل إيجابي ولا يمكن استخدامها كمقياس (علاوة على ذلك ، للتحقق مما إذا كان الأمر كذلك ، ليس لدينا القدرة ولا الرغبة). دلالة بواسطة
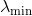
أصغر قيمة لها. ثم يمكننا تصحيح هسه ببساطة عن طريق تحويل جميع القيم الذاتية بها
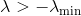
. للقيام بذلك ، ما عليك سوى إضافة المصفوفة إلى Hessian
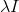
. ثم المعادلة التي تحدد اتجاه النزول سوف تأخذ الشكل
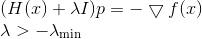
إذا كان لدينا درجة أقل جيدة ل
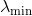
، ثم يمكننا أن نفعل كل ما تم في طرق النسب المتسلسل. ومع ذلك ، إذا لم يكن لدينا مثل هذا التقدير ، ثم أخذ ذلك في الاعتبار مع زيادة

سوف ينخفض طول
p ، يمكننا أن نقول بثقة أن هناك مثل هذا كبير بما فيه الكفاية

هذا في نفس الوقت

إيجابي واضح و

.
لماذا اعتبر هذا الاستنتاج للطريقة غير ناجح للغاية. أولاً ، ليس واضحًا على الإطلاق أن المقياس المصمم بهذه الطريقة مناسب للاستخدام العملي. بالطبع ، يستخدم معلومات حول المشتقات الثانية ، لكنه لا يتبع من أي مكان أن تحويل القيم الذاتية بقيمة معينة لن يجعلها غير قابلة للاستخدام. كما لاحظ الزميل في التعليقات ، يبدو من الواضح أن إضافة مصفوفة هوية متدرجة إلى مصفوفة هسي تؤدي إلى حقيقة أن منطقة الثقة الإهليلجية سوف تميل إلى كروية وهنا مرة أخرى (كما يبدو) مشاكل التشويش في الوادي وغيرها من المسرات ذات النسب المتدرجة والأقارب له طرق. ولكن في الممارسة العملية هذا لا يحدث. على أي حال ، لم أتمكن مطلقًا من ملاحظة أمثلة توضح مثل هذا السلوك. في هذه الحالة ، يطرح السؤال:
ولكن في الواقع ، لماذا ؟
لكن مثل هذا السؤال لا ينشأ إذا نظرنا إلى هذه الطريقة ليس كحالة خاصة لأساليب النزول ، ولكن كطريقة لمنطقة الثقة مع نموذج تربيعي للوظيفة الهدفية ، نظرًا لأن الإجابة واضحة: عندما يزداد اللمدا ، نضغط فقط على المجال - منطقة الثقة لنموذجنا. لا تذهب المعلومات حول الانحناء إلى أي مكان ولا يتم التخلص منها بأي شيء - علينا فقط اختيار حجم المنطقة التي يصف فيها النموذج التربيعي الوظيفة الهدف بشكل مناسب. ويترتب على ذلك أنه بالكاد يستحق توقع تأثير كبير من تغيير في المقياس ، أي شكل منطقة الثقة ، نظرًا لأن كل المعلومات التي لدينا عن الوظيفة الموضوعية قد تم أخذها بالفعل في الاعتبار في نموذجها.
وثانياً ، عند النظر في طريقة ما ، من المهم أن نفهم الفكرة الرئيسية التي قادت Marquardt إلى هذه الطريقة ، وهي فكرة منطقة الثقة. في الواقع ، في التحليل النهائي ، فقط فهم خصوصيات وعموميات الطريقة العددية سيسمح لنا أن نفهم لماذا يعمل ، والأهم من ذلك ، لماذا قد لا تعمل.