يناقش المقال تجربة تطوير برنامج لإنشاء محفظة سندات فعالة من حيث تقليل مدتها . ربما لن أكون أصليًا ولجميع الأشخاص الذين يستثمرون في السندات ، تم حل مشكلات تحديد الأوزان المثالية منذ فترة طويلة ، لكن ما زلت آمل أن تكون الطريقة الموصوفة ورمز البرنامج المقدم مفيدة لشخص ما.

قد تبدو المقالة ، نظرًا لوجود كمية صغيرة من الرياضيات فيها ، معقدة بالنسبة لشخص ما. ولكن إذا كنت قد قررت بالفعل البدء في الاستثمار ، فأنت بحاجة إلى الاستعداد لحقيقة أن الرياضيات غالبًا ما توجد في الواقع المالي بل وأكثر تعقيدًا.

تتوفر التعليمات البرمجية المصدر للبرنامج ومثال محفظة للتحسين على GitHub.

تحديث: كما وعدت ، قدم خدمة ويب بسيطة تجعل البرنامج متاحًا للجميع دون نسخ أو تجميع التعليمات البرمجية.
الرابط
تعليمات للاستخدام في نفس المكان.
إذا لم يعمل شيء ما أو كنت بحاجة إلى إصلاح شيء ما ، فاكتب في التعليقات.

لذلك ، لدينا مهمة تشكيل محفظة فعالة من السندات.

الجزء 1. تحديد مدة المحفظة

من وجهة نظر التقليل إلى أدنى حد من المخاطر غير النظامية (التي تنوع المحفظة من أجلها) ، فقد تم اختيار الأوراق المالية من خلال النظر في معايير قضية معينة ، أو المُصدر (إن لم يكن مقصوراً على OFZ ) ، وسلوك الورقة ، إلخ. (تعتبر الأساليب المتبعة في هذا التحليل فردية تمامًا لكل مستثمر ولا يتم تناولها في هذه المقالة).

بعد اختيار العديد من الأوراق المالية الأفضل للاستثمار ، هناك سؤال طبيعي يطرح نفسه: كم عدد سندات كل إصدار تحتاج إلى شرائها؟ هذه هي مهمة تحسين الحافظة بحيث تكون مخاطر الحافظة محدودة.

من الطبيعي اعتبار المدة كمعلمة محسّنة. وبالتالي ، فإن المهمة هي تحديد وزن الأوراق المالية في المحفظة ، بحيث تكون مدة المحفظة في حدها الأدنى بالنسبة لبعض عائدات المحفظة الثابتة. هنا تحتاج إلى إبداء بعض التحفظات:

1. يتم تحديد مدة محفظة السندات من خلال الأوراق المالية المكونة لها. هذه الفترات معروفة (وهي في المجال العام). مدة المحفظة لا تساوي الحد الأقصى لمدة الأوراق المالية المتضمنة فيه (يوجد مثل هذا الخطأ). العلاقة بين فترات الأوراق المالية الفردية ومدة الحافظة بأكملها ليست علاقة خطية ، أي لا تساوي متوسط ​​المدة الموزونة لسنداتها المكونة (للتحقق من ذلك ، يكفي أن تأخذ في الاعتبار صيغة المدة (انظر (1) أدناه) ومحاولة حساب متوسط ​​المدة الموزونة لمحفظة شرطية تتألف ، على سبيل المثال ، من ورقتين. من كل ورقة ، في الإخراج لا نحصل على صيغة لمدة المحفظة ، ولكن نوع من "الهراء" ، مع اثنين من معدلات الخصم والتدفقات النقدية غير المتسقة كأوزان).
2. على عكس المدة ، يعتمد عائد الحافظة على عائد الأدوات المدرجة فيه خطيًا. أي من خلال وضع الأموال في العديد من الأدوات ذات الدخل الثابت ، سوف نحصل على عائد يتناسب بشكل مباشر مع حجم الاستثمارات في كل أداة (وهذا يعمل بسعر معقد ، وليس فقط بسعر بسيط). تأكد من أن هذا أسهل.
3. يستخدم العائد حتى الاستحقاق ( YTM ) كمعدل العائد على السندات. وعادة ما يستخدم لحساب المدة. ومع ذلك ، فإن العائد حتى تاريخ استحقاق الحافظة بالكامل هنا تعسفي إلى حد ما ، منذ ذلك الحين استحقاق جميع الأوراق المالية هو مختلف. عند تكوين محفظة ، يجب أن تؤخذ هذه الميزة في الاعتبار بمعنى أنه يجب مراجعة الحافظة ، لا تقل عن الأدوات التي تتكون منها ، عن التداول.

لذلك ، فإن المهمة الأولى هي الحساب الصحيح لمدة الحافظة نفسها. الطريقة المباشرة للقيام بذلك هي: تحديد جميع المدفوعات للحافظة ، وحساب العائد حتى الاستحقاق ، ومدفوعات الخصم ، ومضاعفة القيم المستلمة بشروط هذه المدفوعات والإضافة. من أجل القيام بذلك ، تحتاج إلى دمج تقويمات الدفع لجميع الأدوات في تقويم دفعة واحدة للمحفظة بأكملها ، وإنشاء تعبير لحساب العائد حتى تاريخ الاستحقاق ، وحسابه ، وخصمها لكل دفعة ، وضربها في تاريخ استحقاقها ، إضافة ... بشكل عام ، كابوس. إن القيام بذلك حتى بالنسبة للورقتين يعد مهمة شاقة للغاية ، ناهيك عن إعادة حساب الحافظة بانتظام في المستقبل. بهذه الطريقة لا تناسبنا.

لذلك ، من الضروري البحث عن فرصة لتحديد مدة الحافظة بطريقة مختلفة وأسرع. سيكون الخيار المقبول هو الخيار الذي يسمح لك بتحديد مدة الحافظة من خلال فترات الأدوات المعروفة. لقد أظهرت دراسات صيغة المدة أن هناك مثل هذا المسار وهنا أود أن أقدمها بالتفصيل (إذا كان شخص ما غير مهتم بالتفاصيل الرياضية للحسابات ، فيمكنك تخطي بضع فقرات بأمان مع الصيغ والانتقال مباشرة إلى المثال).

يتم تحديد مدة أداة الدين على النحو التالي:

$$عرض $$ $$ \ تبدأ {المعادلة} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~~ (1) \ end {equation} $$ عرض $$

حيث:

• t _i هي لحظة وقت الدفع i ؛
• $$$ inline $ \ start {equation} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {equation} $ inline $ - الدفعة الأولى مخفضة.
• CF _i - i-th payment؛
• ص هو معدل الخصم.

نقدم معامل الخصم k = (1 + r) ونعتبر مبلغ المدفوعات المخصومة P بمثابة دالة k :

$$عرض $$ $ \ تبدأ {المعادلة} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~ ~~~~ (2) \ end {equation} $$ عرض $$

التمييز بين P فيما يتعلق k ، نحصل عليه

$$عرض $$ $$ \ تبدأ {equation} P '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~ (3) \ end {equation} $$ عرض $$

بالنظر إلى الأخير ، يأخذ التعبير عن مدة الرابطة النموذج

$$عرض $$ $$ \ بداية {المعادلة} D = -k \ frac {P '(k)} {P (k)} ~~~~~~~~~~~~~~ (4) \ end {equation} عرض $$ $

في الوقت نفسه ، نتذكر أنه كمعدل خصم r في حالة السند ، يتم استخدام العائد حتى الاستحقاق (YTM).

التعبير الذي تم الحصول عليه صالح لسند واحد ، لكننا مهتمون بمحفظة من السندات. دعنا ننتقل إلى تحديد مدة المحفظة.

نقدم الترميز التالي:

• P _i هو سعر سند i ؛
• z _i - عدد الأوراق المالية للسند i في الحافظة ؛
• k _i - معامل الخصم للسند i في الحافظة ؛
• $$$ inline $ \ تبدأ {equation} P_p = \ sum_ {i} {z_iP_i} \ end {equation} $ inline $ - سعر المحفظة ؛
• $$$ inline $ \ start {equation} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {equation} $ inline $ $ - وزن سند i في الحافظة ؛ شرط واضح$$ $ inline $ \ start {equation} \ sum_ {i} w_i = 1 \ end {equation} $ inline $ .
• $$$ inline $ \ start {equation} k_p = \ sum_ {i} w_ik_i \ end {equation} $ inline $ - معامل خصم الحافظة ؛

بسبب خطي التمايز ، ما يلي صحيح:

$$عرض $$ $$ \ تبدأ {equation} P'_p (k) = \ left (\ sum_ {i} z_iP_i (k) \ right) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~ (5) \ end {equation} $$ عرض $$

وبالتالي ، مع الأخذ في الاعتبار (4) و (5) ، يمكن التعبير عن مدة المحفظة

$$عرض $$ $$ \ تبدأ {equation} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ right) ~~~~~~~~~~~~~~~~ (6) \ end {equation} $$ عرض $$

من (4) يتبع بشكل لا لبس فيه$$ $ inline $ \ تبدأ {equation} P'_j = - \ frac {D_jP_j} {k_j} \ end {equation} $ inline $ .
استبدال هذا التعبير في (6) ، وصلنا إلى الصيغة التالية لمدة المحفظة:

$$عرض $$ $ \ تبدأ {equation} D_p = \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ اليمين) = \ left (\ sum_ {i} w_ik_i \ right) \ left (\ sum_ {j} w_j \ frac {D_j} {k_j} \ right) ~~~~~~~~~~~~~~ (7) \ end {equation} $$ عرض $$

في الظروف التي تكون فيها مدة كل صك وفترة استحقاقه معروفة (ونذكر أننا في مثل هذه الظروف فقط) ، فإن التعبير (7) هو الصيغة المطلوبة لتحديد مدة محفظة الأوراق المالية بناءً على مدة سنداتها. يبدو الأمر معقدًا في المظهر فقط ، ولكنه في الحقيقة جاهز للاستخدام العملي بالفعل بمساعدة أبسط وظائف برنامج MS Excel ، وهو ما سنفعله الآن على سبيل المثال.

مثال

لحساب مدة الحافظة وفقًا للصيغة (7) ، نحتاج إلى إدخال بيانات تتضمن المجموعة الفعلية للأوراق المالية المدرجة في المحفظة ، ومددها والعائد حتى تاريخ الاستحقاق. كما ذكر أعلاه ، هذه المعلومات متاحة للجمهور ، على سبيل المثال ، على rusbonds.ru الموقع في قسم تحليل السندات. مصدر البيانات يمكن تحميلها في شكل اكسل.

على سبيل المثال ، فكر في محفظة أوراق مالية تتكون من 9 سندات. يحتوي جدول البيانات الأصلي الذي تم تنزيله من rusbonds على النموذج التالي.



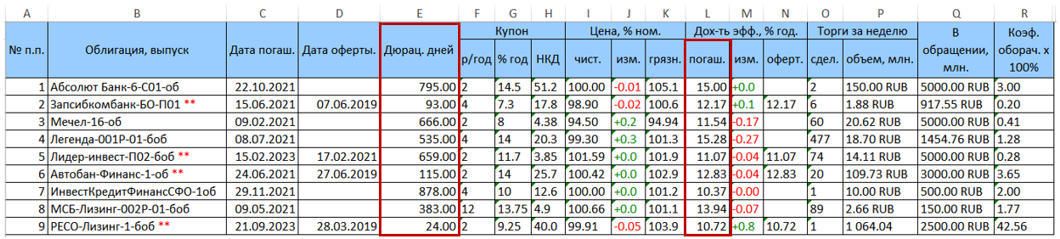
يتم إبراز عمودين من الاهتمام بالنسبة لنا مع مدة (العمود E) والعائد حتى الاستحقاق (العمود L = YTM) باللون الأحمر.

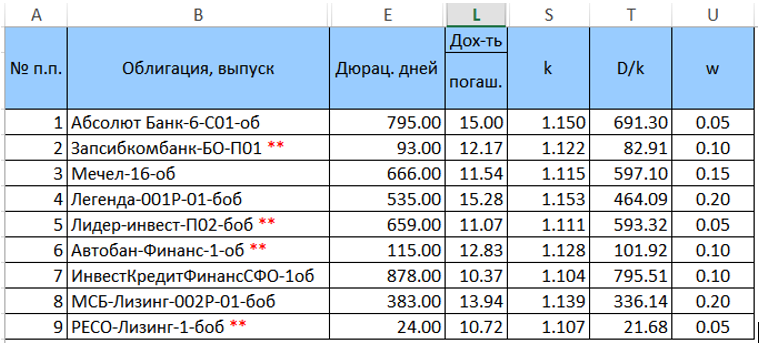
لقد حددنا الأوزان w للسندات في هذه المحفظة (حتى الآن بطريقة تعسفية ، لكن مجموعها يساوي الوحدة) ونحسب k = (1 + YTM / 100) و D / k = ("العمود E" / k). سيبدو الجدول المحول (بدون أعمدة إضافية)



بعد ذلك ، نحسب المنتج$$ $ inline $ \ start {equation} w_j \ frac {D_j} {k_j} \ end {equation} $ inline $ و$$ $ inline $ \ تبدأ {equation} w_ik_i \ end {equation} $ inline $ وجمعها ، واضرب الكميات الناتجة بواحد تلو الآخر. ستكون نتيجة هذا الضرب هي المدة المطلوبة لتوزيع معيّن للأوزان.



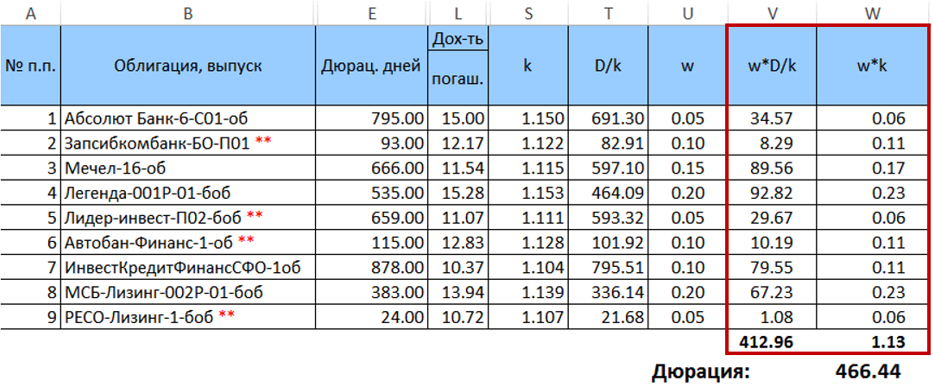
لذلك ، فإن المدة المطلوبة للمحفظة هي 466.44 يومًا. تجدر الإشارة إلى أنه في هذه الحالة بالذات ، تختلف المدة المحسوبة بالصيغة (7) اختلافًا طفيفًا عن متوسط ​​المدة الموزونة المحسوبة بنفس الأوزان (الانحراف <0.5 يوم). ومع ذلك ، يزيد هذا الاختلاف مع زيادة في تشتت الأوزان. سوف يزيد أيضًا مع زيادة انتشار الفترات الورقية.

بعد حصولنا على صيغة حساب مدة المحفظة ، فإن الخطوة التالية هي تحديد وزن الأوراق المالية بحيث تكون المدة المقدرة للمحفظة في عائد معين ضئيلة. ننتقل إلى الجزء التالي - تحسين المحفظة.

الجزء 2. الأمثل محفظة السندات

التعبير (7) هو شكل من الدرجة الثانية ، مع المصفوفة

$$عرض $$ $ \ start {equation} A = \ left \ {k_i \ frac {D_j} {k_j} \ right \} = \ start {pmatrix} D_1 & \ ldots & k_1 \ frac {D_n} {k_n} \ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {equation} $$ عرض $$

وفقا لذلك ، في شكل مصفوفة ، يمكن كتابة التعبير عن مدة المحفظة (7) على النحو التالي:

$$عرض $$ $$ \ تبدأ {المعادلة} D_p = w ^ TAw ~~~~~~~~~~~~~~ (8) \ end {equation} $$ عرض $$

حيث w هو ناقل عمود أوزان السندات في الحافظة. كما ذكر أعلاه ، يجب أن يكون مجموع عناصر المتجه w مساوياً للوحدة. من ناحية أخرى ، فإن التعبير $$$k_p = \ sum_ {i} w_i k_i$ (والذي يعتبر في جوهره منتجًا عدديًا بسيطًا ( w ، k ) ، حيث k هو ناقل معاملات خصم السندات) يجب أن يكون مساوياً لمعدل الخصم المستهدف للمحفظة ، وبالتالي يجب تحديد عائد المحفظة المستهدف.

وبالتالي ، فإن مهمة تحسين محفظة السندات هي تقليل الوظيفة التربيعية (8) مع قيود خطية.

الطريقة الكلاسيكية لإيجاد الحد الأقصى الشرطي لوظيفة من عدة متغيرات هي طريقة Lagrange المضاعفة. ومع ذلك ، لا تنطبق هذه الطريقة هنا ، إذا كان السبب في ذلك هو أن المصفوفة A تتحلل عن طريق البناء (ولكن ليس فقط بسبب ذلك ؛ فنحن نتجاهل تفاصيل تحليل قابلية تطبيق طريقة Lagrange هنا حتى لا نفرط في تحميل المحتوى بالمحتوى الرياضي المفرط).

عدم القدرة على تطبيق طريقة تحليلية سهلة وبأسعار معقولة يؤدي إلى الحاجة إلى استخدام الأساليب العددية. مشكلة تحسين الوظيفة التربيعية معروفة جيدًا ولديها العديد من الخوارزميات الفعالة المطورة منذ فترة طويلة والمطبقة في المكتبات العامة.

لحل هذه المشكلة بالذات ، تم استخدام مكتبة ALGLIB وخوارزميات التحسين التربيعية المنفذة فيه ، QP-Solvers ، المتضمنة في حزمة minqp.

مشكلة التحسين التربيعي بشكل عام هي كما يلي:

من الضروري إيجاد متجه n ثلاثي الأبعاد يعمل على تقليل الوظيفة

$$عرض $$ $ \ تبدأ {المعادلة} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~~ (9) \ end {equation} عرض $$ $

مع قيود معينة
1)
2) Cw * d ؛
حيث w ، l ، u ، d ، b عبارة عن متجهات ذات قيمة حقيقية ذات أبعاد n ، Q هي المصفوفة المتماثلة للجزء التربيعي ، والإشارة * تعني أي من العلاقات ≥ = ≤.
كما يتضح من (8) ، فإن الجزء الخطي b ^T w في وظيفتنا الهدفية يساوي الصفر. ومع ذلك ، فإن المصفوفة A ليست متماثلة ، ومع ذلك ، لا تمنعها من الوصول إلى شكل متماثل دون تغيير الوظيفة نفسها. للقيام بذلك ، فقط وضعت بدلا من ألف التعبير$$ $ inline $ \ start {equation} \ frac {A ^ T + A} {2} \ end {equation} $ inline $ منذ الصيغة (9) تشمل المعامل $$$\ frac {1} {2}$ ثم نحن س يمكننا قبول $$$A ^ T + A$ .

تحدد إحداثيات المتجهات l و u حدود المتجه المرغوب وتقع في النطاق [-1،1]. نظرًا لأننا لا نفترض مبيعات قصيرة للسندات ، فإن إحداثيات المتجهات في حالتنا لا تقل عن 0. في المثال التالي ، للبساطة ، يفترض أن المتجه l يساوي الصفر ، وتكون معاملات المتجه u كلها 0.3 . ومع ذلك ، لا شيء يمنعنا من تحسين البرنامج وجعل ناقلات القيد أكثر قابلية للتخصيص.

ستتألف المصفوفة C في حالتنا من سطرين: 1) معاملات الخصم ، والتي عند ضربها بشكل كبير بالأوزان (نفس ( w ، k )) ، ينبغي أن تعطي معدل العائد المستهدف للمحفظة ؛ 2) سلسلة تتكون من وحدات. هناك حاجة لوضع حدود $$$\ sum_ {i} w_i = 1$ .

وهكذا ، فإن تعبير Cw * d لمهمتنا سيبدو كما يلي:

$$عرض $$ $$ \ بدء {المعادلة} \ اليسار \ {\ بدء {مجموعة} {ccc} ({\ bf w، k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \ صحيح. ~~~~~~~~~~~~~ (10) \ end {equation} $$ عرض $$

ننتقل الآن إلى تنفيذ برنامج البحث عن الحافظة المثلى. أساس المحسن التربيعي في ALGLIB هو الكائن $$$\ tt \ small minqpstate$

alglib::minqpstate state; 

لتهيئة المُحسّن ، يتم تمرير هذا الكائن إلى وظيفة minqpcreate مع معلمة بُعد المهمة n

 alglib::minqpcreate(n, state); 

النقطة التالية الأكثر أهمية هي اختيار خوارزمية التحسين (حلالا). تقدم مكتبة ALGLIB للتحسين التربيعي ثلاثة حلول:

• QP-BLEIC هي الخوارزمية الأكثر عالمية المصممة لحل المشكلات التي لا تحتوي على عدد كبير من القيود الخطية (حتى 50 وفقًا لتوصيات الوثائق) (من النموذج Cw * d ). في الوقت نفسه ، يمكن أن يكون فعالًا في المهام ذات البعد الكبير (كما تدعي الوثائق - حتى n = 10000).
• QuickQP هي خوارزمية فعالة للغاية ، خاصةً عندما يتم تحسين وظيفة محدبة. ومع ذلك ، لسوء الحظ ، لا يمكن أن تعمل مع قيود خطية - فقط مع الظروف الحدودية (من النموذج l≤w≤u ).
• الكثافة - AUL - الأمثل لحالة الأبعاد كبيرة جدا وعدد كبير من القيود. ولكن وفقًا للوثائق ، سيتم حل المهام ذات البعد الصغير وعدد القيود بشكل أكثر كفاءة باستخدام خوارزميات أخرى.

بالنظر إلى الخصائص المذكورة أعلاه ، فمن الواضح أن حلالا QP-BLEIC هو الأنسب لمهمتنا.

لإرشاد المحسّن لاستخدام هذه الخوارزمية ، يجب عليك استدعاء الوظيفة $$$\ tt \ minqpsetalgobleic $ الصغير$ . يتم تمرير الكائن نفسه ومعايير التوقف إلى هذه الوظيفة ، والتي لن نتطرق إليها بمزيد من التفصيل: في البرنامج الذي تم النظر فيه هنا ، يتم استخدام القيم الافتراضية. استدعاء الوظيفة كما يلي:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

يتضمن التهيئة الإضافية للمحلّل:

• نقل مصفوفة الجزء التربيعي Q - $$$\ tt \ small alglib :: minqpsetquadraticterm (state، qpma)؛$
• انتقال ناقل الجزء الخطي (في حالتنا ، ناقل الصفر) - $$$\ tt \ small alglib :: minqpsetlinearterm (state، b)؛$
• نقل حالة الحدود المتجهات l و u - $$$\ tt \ small alglib :: minqpsetbc (الحالة ، bndl ، bndu) ؛$
• ناقل الحركة الخطي - $$$\ tt \ small alglib :: minqpsetlc (state، c، ct)؛$
• تحديد مقياس تنسيق مساحة المتجه $$$\ tt \ small alglib :: minqpsetscale (state، s)؛$

دعونا نتناول كل بند:
لتحديد المتجهات والمصفوفات ، تستخدم مكتبة ALGLIB كائنات من الأنواع الخاصة (عدد صحيح وقيمة حقيقية): $$$\ tt \ small alglib :: integer \ _1d \ _array$ . $$$\ tt \ small alglib :: real \ _1d \ _array$ . $$$\ tt \ small alglib :: integer \ _2d \ _array$ . $$$\ tt \ small alglib :: real \ _2d \ _array$ . لإعداد المصفوفة ، نحن بحاجة إلى نوع $$$\ tt \ small الحقيقي \ _2d \ _array$ . في البرنامج ، قم أولاً بإنشاء مصفوفة A ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpma$ ) ، ومن ثم وفقا للصيغة $$$Q = A ^ T + A$ منه نقوم ببناء المصفوفة Q ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpmq$ ). يعد تحديد أبعاد المصفوفة في ALGLIB وظيفة منفصلة $$$\ tt \ setlength الصغيرة (n، m)$ .

لبناء المصفوفات ، نحتاج إلى متجه معاملات الخصم ( k _i ) وعلاقة المدة بهذه المعاملات ( $$$\ frac {D_j} {k_j}$ ):

 std::vector<float> disfactor; std::vector<float> durperytm; 

يظهر مقتطف الكود الذي ينفذ بناء المصفوفات في القائمة التالية:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

متجه الجزء الخطي ، كما هو موضح بالفعل ، هو صفر في حالتنا ، لذلك كل شيء بسيط معه:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

تنتقل شروط حدود المتجهات بواسطة وظيفة واحدة. لحل هذه المشكلة ، يتم تطبيق شروط حدودية بسيطة للغاية: يجب ألا يقل وزن كل ورقة عن الصفر (لا نسمح بالمواقع السلبية) ويجب ألا يتجاوز 30٪. إذا رغبت في ذلك ، يمكن أن تكون القيود معقدة. أظهرت تجارب البرنامج أنه حتى التغيير البسيط في هذا النطاق يمكن أن يؤثر بشكل كبير على النتائج. وبالتالي ، فإن زيادة الحد الأدنى و / أو النقصان في الحد العلوي يؤدي إلى تنويع أكبر للحافظة النهائية ، لأنه أثناء التحسين يمكن للحامل أن يستبعد بعض الأوراق المالية من المتجه الناتج (يعينهم وزنًا 0٪) غير مناسب. إذا قمت بتعيين الحد الأدنى للجداول ، على سبيل المثال ، عند 5٪ ، فسيتم ضمان تضمين جميع الأوراق في الحافظة. ومع ذلك ، فإن المدة المحسوبة في مثل هذه الإعدادات ستكون ، بالطبع ، أكبر مما كانت عليه في الحالة التي يمكن فيها للمحسن استبعاد الورق.

لذلك ، يتم تعيين شروط الحدود بواسطة متجهين ونقلها إلى حلالا:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

بعد ذلك ، يحتاج المُحسِّن إلى تجاوز القيود الخطية المحددة بواسطة النظام (10). في ALGLIB ، يتم ذلك باستخدام الوظيفة $$$\ tt \ small alglib :: minqpsetlc (state، c، ct)$ ، حيث c هي المصفوفة التي تجمع بين الجانبين الأيسر والأيمن من النظام (10) ، أي عرض المصفوفة $$$(C ~~ d)$ و ct هي متجه العلاقات (على سبيل المثال ، مراسلات النموذج ≥ أو = أو ≤). في حالتنا ، ct = (0،0) ، والتي تتوافق مع النسبة '=' لكلا صفوف النظام (10).

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

تنصح وثائق مكتبة ALGLIB بشدة بتعيين مقياس المتغيرات قبل بدء تشغيل المحسن. هذا مهم بشكل خاص إذا تم قياس المتغيرات بالوحدات ، والتي يختلف تغييرها حسب أوامر الحجم (على سبيل المثال ، عند البحث عن حل ، يمكن تغيير الأطنان بالمئات أو الألف ، والمتر بالوحدات ؛ يمكن حل المشكلة في مساحة الأطنان) مما يؤثر على معايير التخلي. ومع ذلك ، هناك تحفظ أنه مع نفس تحجيم المتغيرات ، فإن ضبط المقياس ليس ضروريًا. في البرنامج قيد النظر ، ما زلنا ننفذ مهمة الحجم من أجل مزيد من الصرامة في النهج ، خاصة وأن الأمر بسيط للغاية.

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

بعد ذلك ، وضعنا للمحسن نقطة انطلاق. بشكل عام ، هذه الخطوة اختيارية أيضًا ، ويتكيف البرنامج بنجاح مع المهمة دون نقطة بداية محددة بوضوح. وبالمثل ، لأسباب الصرامة ، وضعنا نقطة البداية. لن نكون أذكياء: ستكون نقطة البداية هي النقطة التي لها نفس الأوزان لجميع السندات.

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

يبقى تحديد المتغير الذي سيعود إليه المحسن إلى الحل الموجود ومتغير الحالة. ثم يمكنك تشغيل التحسين ومعالجة النتيجة

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

بشكل خاص ، لم يتم قياس وقت تشغيل البرنامج في التجارب ، ولكن كل شيء يعمل بسرعة كبيرة. في الوقت نفسه ، من الواضح أنه من غير المرجح أن يقوم المستثمر الخاص بتحسين محفظة تضم أكثر من 10-15 سندات.

من المهم أيضًا ملاحظة ما يلي. إرجاع المحسن بدقة متجه الأوزان. للحصول على المدة المحسوبة نفسها ، يجب عليك استخدام الصيغة (8) مباشرةً. يمكن للبرنامج القيام بذلك. لهذا الغرض ، تم إضافة وظيفتين لمتجهات الضرب والمصفوفات بشكل خاص. لن نعطيهم هنا. أولئك الذين يتمنون أن يجدوا أنفسهم بسهولة في أكواد المصدر المنشورة.

هذا كل شيء. استثمار فعال في أدوات الدين للجميع.

ملاحظة: إن فهم رمز شخص آخر ليس الوظيفة الأكثر جاذبية ، وبالنسبة للعديد من الأشخاص الذين يرغبون في الاستثمار ، فهو ليس متخصصًا على الإطلاق ، سأحاول تحويل هذا البرنامج لاحقًا إلى خدمة ويب بسيطة يمكن للجميع استخدامها ، بغض النظر عن معرفتهم بالرياضيات والبرمجة.