 الترجمة الأصلية في مدونتي
الترجمة الأصلية في مدونتيستيفن وولفرام بث المسابقة المباشرة (باللغة الإنجليزية) موقع المسابقةدعنا نوضح للقراء ما تعنيه "القاعدة 30" - إنها آلية أولية خلوية (انظر ويكي ) ، تم تعيين حالتها (قاعدة إنشاء مستوى جديد من الخلايا على أساس القديم) في نظام الأرقام الثنائية على أنها 0-0-0-1-1-1 -1-0 ، والتي يمكن تفسيرها على أنها 30 بتدوين عشري.
إذن من أين بدأ كل شيء؟ - "القاعدة 30"
كيف يمكن أن يكون شيء
بسيط لا يصدق ينتج شيئًا معقدًا بشكل لا يصدق ؟ لقد مر ما يقرب من 40 عامًا منذ أن
تعرفت للمرة الأولى على المادة 30 ، لكنها ما زالت تدهشني وتسعدني. لفترة طويلة ، أصبح اكتشافي الشخصي المفضل في
تاريخ العلوم ، على مر السنين غيرت رؤيتي للعالم بأكملها وقادني إلى مجموعة
متنوعة من أنواع جديدة من فهم العلوم والتكنولوجيا والفلسفة وأكثر من ذلك بكثير .
ولكن حتى بعد سنوات عديدة ، لا يزال هناك الكثير من المفاهيم الأساسية حول القاعدة 30 التي لا يزال يتعذر علينا الوصول إليها. لذلك قررت أن الوقت قد حان للقيام بكل ما هو ممكن لتحفيز عملية تحديد المجموعة الأساسية من هذه الأنماط الأساسية.
لذا ، فإنني أقدم اليوم لمقدمي الطلبات 30،000 دولار كجائزة إجمالية للإجابة على الأسئلة الرئيسية الثلاثة حول القاعدة 30.
المادة 30 بسيطة للغاية:
هناك تسلسل من صفوف الخلايا السوداء والبيضاء (الخلايا) ، ومع مراعاة صف معين من الخلايا السوداء والبيضاء ، يتم تحديد ألوان الخلايا في الصف أدناه ، مع مراعاة كل خلية على حدة والخلايا المجاورة لها ، ثم يتم تطبيق قاعدة الاستبدال البسيطة التالية عليها ، وهي:

قانونRulePlot[CellularAutomaton[30]]
[شاهد الفيديو ، الذي يخبر في دقيقتين جوهر الأوتوماتة الخلوية والقاعدة 30 - ملاحظة المترجم]
ماذا يحدث إذا بدأت بخلية سوداء واحدة؟ [
يتم أخذ صف من الخلايا البيضاء ، بلا حدود على كلا الجانبين وخلية سوداء واحدة ، ثم تنطبق القواعد الموضحة أعلاه على هذا الصف ، ويتم الحصول على صف جديد ، وما إلى ذلك - ملاحظة المترجم ] افترض (كما فعلت أنا في البداية) أن القاعدة بسيطة للغاية ، ويجب أن يكون القالب الذي يتم الحصول عليه على أساس عمله بسيطًا جدًا. ومع ذلك ، إذا أجريت تجربة ، فسترى ما يحدث بعد الخطوات الخمسين الأولى من الخوارزمية:

قانونRulePlot[CellularAutomaton[30], {{1}, 0}, 50, Mesh -> All,
ImageSize -> Full]
وبطبيعة الحال ، يمكننا أن نفترض أنه نتيجة للخوارزمية ، سيتم الحصول على كائن رياضي أبسط بكثير. ومع ذلك ، إليك ما يحدث بعد الخطوات الـ 300 الأولى:

هذا يدل على أن هناك
نمط معين
- على الجانب الأيسر من الهرم . لكن في الوقت نفسه ،
تبدو العديد من جوانب هذا القالب
وكأنه شيء تم تكوينه بشكل عشوائي .
من غير المفهوم أن مثل هذه القاعدة البسيطة يمكن أن تؤدي في النهاية إلى مثل هذا السلوك المعقد للنظام. بناءً على ذلك ، توصلت إلى استنتاج مفاده
أنه في عالم الحوسبة لجميع برامج الكمبيوتر الممكنة ، فإن هذا السلوك شائع جدًا ، بل إنه يوجد في كل مكان تقريبًا.
بناءً على هذه الفرضية ، قمت بتطوير نهج لتشكيل
نوع جديد تمامًا
من العلوم - استنادًا إلى
مبادئ مراقبة تشغيل الخوارزميات البسيطة.
تدريجيا ، المزيد من الأدلة كان تراكم هذه المبادئ.
ومع ذلك ، دعنا نعود إلى القاعدة 30 ونفحص بالتفصيل ما الذي يسمح لنا به بالضبط ، وما هو استخدامه؟ ما الذي يمكن قوله بالضبط عن سلوك هذه الخوارزمية؟ من الواضح على الفور أنه حتى الإجابات على الأسئلة الأكثر وضوحا تتضح أنها صعبة.
حتى بعد عقود من عدم العثور على إجابات ، قررت أن الوقت قد حان لطرح بعض الأسئلة المحددة حول القاعدة 30 ، مع تحفيز هذا المجال بجوائز نقدية خطيرة.
لقد حاولت بالفعل القيام بشيء مماثل في عام 2007 ، حيث
وضعت جائزة للإجابة على السؤال الأساسي حول جهاز
Turing معين. وفي هذه الحالة ، كانت النتيجة إيجابية ولم تستغرق وقتًا طويلاً للانتظار. بعد بضعة أشهر فقط ،
تم الفوز بهذه
الجائزة - بعد أن أثبتت إلى الأبد ما هي أبسط ماكينات تورينج العالمية الممكنة ، كما أثبتت بشكل مقنع للغاية
المبدأ العام
للتكافؤ الحسابي ، الذي طورته شخصيًا في وقت سابق.
تحدد مسابقة القاعدة 30 مرة أخرى هدف حل مهمة أساسية ، وهي: ما
مدى تعقيد سلوك القاعدة 30 ؟ كل مهمة تطرح سؤالاً في هذا المجال بطريقتها الخاصة وعلى وجه التحديد. مثل القاعدة 30 نفسها ، فهي كلها مضللة في الإعداد الأصلي. ومع ذلك ، فإن حل أي منها سيكون إنجازًا كبيرًا ، والذي سيساعد في النهاية على إلقاء الضوء على المبادئ الأساسية لخصائص تكوين الكون الحاسوبي ، والتي تتجاوز بكثير تفاصيل القاعدة 30.
لقد
عملت على كل من هذه القضايا لأكثر من 35 عامًا . وطوال هذا الوقت ، حاولت أن أجد الفكرة الصحيحة في إطار التفكير الرياضي الحسابي أو الحسابي الثابت ، بهدف حل واحد على الأقل من هذه المشكلات. الآن أريد أن أفتح هذه العملية أمام المجتمع العالمي بأسره. ومع ذلك ، سأكون مهتمًا بمعرفة ما يمكن تحقيقه في حل هذه المشكلات ، والطرق التي يمكن استخدامها في هذه الحالة.
المادة 30 - المهام المطلوب حلها
بالنسبة للمهام التنافسية بموجب المادة 30 ، أعطي الأولوية لأحد السمات الرئيسية لخوارزمية القاعدة 30 ، وهي:
العشوائية الواضحة لتشكيل خلايا العمود المركزي . ابدأ بخلية سوداء واحدة ، ثم ألق نظرة على تسلسل قيم ألوان الخلايا في هذا العمود وستصل إلى استنتاج أنها عشوائية:

قانونArrayPlot[
MapIndexed[If[#2[[2]] != 21, # /. {0 -> 0.2, 1 -> .6}, #] &,
CellularAutomaton[30, {{1}, 0}, 20], {2}], Mesh -> All]
ولكن بأي معنى هم
"عشوائية حقا" ؟ وهل يمكن إثبات هذا الافتراض؟ تستخدم كل مهمة من المهام المحددة في إطار المسابقة معيار العشوائية الخاص بها ، وبعد ذلك تسأل عما إذا كان التسلسل عشوائيًا وفقًا لهذا المعيار.
المهمة 1: هل يبقى العمود المركزي دائمًا غير دوري؟
النظر في بداية العمود المركزي من المادة 30:

قانونArrayPlot[List@CellularAutomaton[30, {{1}, 0}, {80, {{0}}}],
Mesh -> True, ImageSize -> Full]
ليس من الصعب العثور على أن القيم في هذا العمود لا تتكرر - إنها ليست دورية. ولكن التحدي هو ، هل يصبح العمود المركزي دوريًا على الإطلاق؟ من خلال إطلاق القاعدة 30 ، نرى أن التسلسل لا يصبح دوريًا حتى في المراحل
الأولى من البليون . ما يجب القيام به من أجل إنشاء وإثبات هذا بشكل مؤكد.
هنا هو الرابط حيث توجد
أول مليون وأول مليار قيمة لهذا التسلسل (
مستودع بيانات Wolfram ).
المهمة 2: هل كل لون من خلايا (أسود أو أبيض) في المتوسط من المرجح بنفس القدر في العمود الأوسط؟
هذا هو ما نحصل عليه عندما نحسب عدد الخلايا السوداء والبيضاء بالتتابع في خطوات أكثر في العمود المركزي لخوارزمية القاعدة 30:

قانونDataset[{{1, 1, 0, ""}, {10, 7, 3, 2.3333333333333335}, {100, 52, 48, 1.0833333333333333},
{1000, 481, 519, 0.9267822736030829}, {10000, 5032, 4968, 1.0128824476650564},
{100000, 50098, 49902, 1.0039276982886458}, {1000000, 500768, 499232,
1.003076725850907}, {10000000, 5002220, 4997780, 1.0008883944471345},
{100000000, 50009976, 49990024, 1.000399119632349},
{1000000000, 500025038, 499974962, 1.0001001570154626}}]
النتائج قريبة بالتأكيد من تساوي الخلايا السوداء والبيضاء. هنا المشكلة (سؤال المشكلة) هي مسألة
ما إذا كانت هذه العلاقة تتقارب مع 1 مع زيادة عدد الخطوات في الدورة .
المهمة 3: هل يتطلب حساب الخلية n للعمود المركزي عمليات O ( n ) على الأقل؟
للعثور على الخلية
n في العمود الأوسط ، يمكنك دائمًا تشغيل القاعدة 30 لخطوات
n ، بحساب قيم جميع الخلايا داخل الماس المحددة في الشكل أدناه:

قانونWith[{n = 100},
ArrayPlot[
MapIndexed[If[Total[Abs[#2 - n/2 - 1]] <= n/2, #, #/4] &,
CellularAutomaton[30, CenterArray[{1}, n + 1], n], {2}]]]
ولكن إذا قمت بذلك مباشرة ، فستفعل ذلك
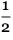 n 2
n 2 تحديثات خلية منفصلة ، وبالتالي ، فإن قوة الحوسبة المطلوبة تزيد مثل O (
n 2 ). مسألة هذه المشكلة هي
ما إذا كان هناك أكثر (أو أكثر) طريقة أسرع لحساب قيمة الخلية nth دون جميع العمليات الحسابية الوسيطة - أو ، على وجه الخصوص ، في أقل من O ( n ) العمليات .
الأرقام التي تشكل بي
القاعدة 30 هي نتاج لعالم الحوسبة: نظام قائم على دراسة البرامج البسيطة الممكنة ذات الهيكل الفكري الجديد ، والذي يوفره نموذج الحوسبة. ومع ذلك
، فإن المهام التي حددتها في مسابقة المادة 30 لها نظائرها في الرياضيات ، والتي كانت موجودة منذ قرون .
النظر في
قيم الأرقام في الرقم بي . يشبه سلوك هذه الأرقام توليد البيانات في العمود المركزي لخوارزمية القاعدة 30. أي أن هناك خوارزمية معينة لحسابها ، وبمجرد صياغتها ، فإنها تبدو عشوائية تقريبًا لأية مهام.
![N [Pi، 85] N[Pi, 85]](https://habrastorage.org/getpro/habr/post_images/49e/ae6/17d/49eae617de3c0c9a864d4624413c6ce8.png)
فقط لجعل التناظرية أقرب قليلاً ، إليك الأرقام القليلة الأولى من Pi في نظام الأرقام مع القاعدة 2:
![BaseForm [N [Pi، 25]، 2] BaseForm[N[Pi, 25], 2]](https://habrastorage.org/getpro/habr/post_images/18e/d4b/8f6/18ed4b8f6fd778443cc62470ea0956a9.png)
قانونBaseForm[N[Pi, 25], 2]
وإليك البتات القليلة الأولى في العمود الأوسط من المادة 30:
![صف [CellularAutomaton [30 ، {{1} ، 0} ، {90 ، {{0}}}] Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]](https://habrastorage.org/getpro/habr/post_images/9e9/f64/a52/9e9f64a521480621d3adbb859609742a.png)
قانونRow[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]
للمتعة ، يمكنك تحويلها إلى رقم عشري:
![N [FromDigits [{Flatten [CellularAutomaton [30، {{1}، 0}، {500، {0}}]]، 0}، 2]، 85] N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]], 0}, 2], 85]](https://habrastorage.org/getpro/habr/post_images/0df/d67/782/0dfd677828ca278c971d267948d88ad3.png)
قانونN[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]],
0}, 2], 85]
بطبيعة الحال ، فإن الخوارزميات المعروفة لحساب أرقام Pi أكثر تعقيدًا من القاعدة البسيطة نسبيًا لتوليد الخلايا في العمود المركزي من المادة 30. لذا ، ماذا نعرف عن الأرقام في Pi؟
أولاً ، نحن نعلم أنها لا تتكرر. وقد ثبت هذا مرة أخرى في الستينيات من القرن الثامن عشر ، عندما تبين
أن Pi رقم غير عقلاني ، لأن الأرقام الوحيدة التي تتكرر فيها الأرقام هي أرقام عقلانية. (في عام
1882 ، أظهر أيضًا
أن Pi متسامٍ ، أي أنه لا يمكن التعبير عنها من خلال جذور كثيرات الحدود).
إذن ما نوع القياس الذي يمكن استخلاصه عند صياغة المشكلة 2؟ هل نعلم أنه في سلسلة من أرقام
Pi ، تحدث أرقام مختلفة بنفس التردد؟ حتى الآن
، تم حساب أكثر من
100 تريليون رقم ثنائي - وترددات الأرقام المقاسة قريبة جدًا (في أول
40 تريليون رقم ثنائي من Pi ، تبلغ نسبة الوحدات إلى الأصفار 0.99999998064 تقريبًا). ولكن عند حساب الحد ، هل ستكون الترددات هي نفسها بالضبط؟ لطالما طرح العلماء هذا السؤال لعدة قرون ، لكن الرياضيات لم تتمكن حتى الآن من الإجابة عليه.
بالنسبة للأرقام المنطقية ، تكون تسلسلات الأرقام المكونة لها دورية ، ومن السهل تحديد الترددات النسبية لحدوث هذه الأرقام في رقم. ومع ذلك ، بالنسبة لتسلسل أرقام جميع الأرقام الأخرى "التي تم إنشاؤها بواسطة الطبيعة (التي تم إنشاؤها بشكل طبيعي)" ، في معظم الحالات ، لا يُعرف عمليا أي شيء عن ماهية ترددات الأرقام المدرجة في الرقم. سيكون من المنطقي أن نفترض أن أرقام Pi (وكذلك العمود المركزي من القاعدة 30) في الواقع "
طبيعية " بمعنى أنه لا يقتصر فقط على كل رقم فردي ، بل وأي كتلة من أرقام ذات طول معين تقابل نفس التردد المحدد. وكما لوحظ في الأعمال المتعلقة بهذا الموضوع من ثلاثينيات القرن العشرين ، من الممكن تمامًا "إنشاء بنية رقمية (نموذج)" بالأرقام العادية.
ثابت Champernone الذي تم الحصول عليه عن طريق الجمع بين أرقام الأعداد الصحيحة المتتالية هو مثال على التعليل أعلاه (يمكن الحصول على نفس الشيء على أساس أي عدد طبيعي من خلال الجمع بين قيم وظائف الأعداد الصحيحة المتتالية):
![N [ChampernowneNumber [10]، 85] N[ChampernowneNumber[10], 85]](https://habrastorage.org/getpro/habr/post_images/253/f93/8f3/253f938f3261e70f8985a49bf1158dde.png)
قانونN[ChampernowneNumber[10], 85]
تجدر الإشارة إلى أن النقطة هنا هي أنه بالنسبة للأرقام "المبنية بشكل طبيعي" التي يتم تشكيلها من خلال مجموعات من الوظائف الرياضية القياسية ، لا يوجد مثال واحد مكتشف حيث يمكن العثور على أي تسلسل منتظم للأرقام. بطبيعة الحال ، في النهاية ، يعتمد هذا الحكم على ما هو المقصود بـ "الانتظام" ، وفي مرحلة ما تتحول المهمة إلى نوع من البحث
الرقمي إلى التمثيلي بحثًا عن ذكاء خارج كوكب الأرض . ومع ذلك ، لا يوجد دليل على أنه من غير الممكن ، على سبيل المثال ، العثور على مجموعة معقدة من الجذور التربيعية التي تحتوي على سلسلة من الأرقام مع انتظام واضح للغاية.
أخيرًا ، فكر في تناظر المشكلة 3 لـ Pi؟ على عكس القاعدة 30 ، حيث أن الطريقة الواضحة لحساب العناصر في التسلسل هي خطوة واحدة في كل مرة ، فإن الطرق التقليدية لحساب أرقام Pi تشمل الحصول على أفضل التقريب ل Pi كرقم دقيق. مع السلسلة القياسية ("الغريبة") التي اخترعها
رامانوجان في عام 1910 والتي تم تحسينها من
قبل الأخوين تشودنوفسكي في عام 1989 ، فإن الأعضاء القلائل الأوائل في هذه السلسلة يقدمون التقديرات التالية:

قانونStyle[Table[N[(12*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(k\)]*\(\((6*k)\)!\)*\((13591409 +
545140134*k)\)\), \(\(\((3*k)\)!\)
\*SuperscriptBox[\((\(k!\))\), \(3\)]*
\*SuperscriptBox[\(640320\), \(3*k + 3/2\)]\)]\))^-1, 100], {n, 10}] //
Column, 9]
إذن كم عدد العمليات اللازمة للعثور على الرقم
التاسع ؟ عدد المصطلحات المطلوبة في الصف هو O (
n ). ولكن يجب حساب كل شرط بدقة
رقمية ، والتي تتطلب على الأقل O (
n ) عمليات حسابية منفصلة ، مما يعني ضمنا أن أعباء العمل الحسابية العامة ستكون أكبر من O (
n ).
حتى التسعينيات ، كان من المفترض أنه لا توجد طريقة لحساب الرقم
التاسع لبي دون حساب جميع الأرقام السابقة. ولكن في عام 1995 ، اكتشف
سيمون بلاف أنه من الممكن فعلاً حساب ، على الرغم من وجود بعض الاحتمالات ، الرقم
الخالي دون حساب الأرقام السابقة. وعلى الرغم من أن المرء يعتقد أن هذا سيسمح بالحصول على الرقم
التاسع في أقل من O (
n ) ، فإن حقيقة أنك تحتاج إلى إجراء حسابات بدقة من الأرقام تعني أن
O على الأقل
( n) ) العمليات.
النتائج والقياسات والحدس
المهمة 1: هل يبقى العمود المركزي دائمًا غير دوري؟
من بين الجوائز الثلاث في مسابقة القاعدة 30 ، هذه هي الجائزة التي تحقق فيها بالفعل معظم التقدم المحرز في حل هذه المشكلة. نظرًا لأنه لا يزال من غير المعروف ما إذا كان العمود المركزي للقاعدة 30 سيصبح دوريًا ، فقد
أظهرت إريكا جين في عام 1986 أنه لا يمكن أن يكون هناك عمودين دوريان. وفي الحقيقة هذا صحيح ، ويمكن للمرء أن يجادل مؤيدًا لحقيقة
أن عمودًا واحدًا مع خلايا فردية في عمود آخر لا يمكن أن يكون دوريًا .
يستخدم إثبات زوج الأعمدة سمة من سمات القاعدة 30. خذ بعين الاعتبار بنية القاعدة:
![RulePlot [CellularAutomaton [30]] RulePlot[CellularAutomaton[30]]](https://habrastorage.org/getpro/habr/post_images/5fa/ca7/858/5faca785893d90e7969ef2a4dad73c58.png)
قانونRulePlot[CellularAutomaton[30]]
من الممكن القول ببساطة أنه بالنسبة لكل ثلاثية من الخلايا ، تحدد القاعدة لون الخلية المركزية بها ، لكن بالنسبة للقاعدة 30 ، يمكنك أيضًا تنفيذ القاعدة بشكل فعال على الجانب: مع مراعاة الخلية الموجودة على اليمين وما فوقه ، يمكنك أيضًا تحديد لون الخلية على اليسار بشكل فريد. هذا يعني أنه إذا كنت تأخذ عمودين متجاورين ،
فيمكنك استعادة القالب بالكامل على اليسار :

قانونGraphicsRow[
ArrayPlot[#, PlotRange -> 1, Mesh -> All, PlotRange -> 1,
Background -> LightGray,
ImageSize -> {Automatic, 80}] & /@ (PadLeft[#, {Length[#], 10},
10] & /@
Module[{data = {{0, 1}, {1, 1}, {0, 0}, {0, 1}, {1, 1}, {1,
0}, {0, 1}, {1, 10}}},
Flatten[{{data},
Table[Join[
Table[Module[{p, q = data[[n, 1]], r = data[[n, 2]],
s = data[[n + 1, 1]] },
p = Mod[-q - r - qr + s, 2];
PrependTo[data[[n]], p]], {n, 1, Length[data] - i}],
PrependTo[data[[-#]], 10] & /@ Reverse[Range[i]]], {i, 7}]},
1]])]
ومع ذلك ، إذا كانت الأعمدة تحتوي على بنية دورية ، فسيتبع ذلك على الفور أن القالب المستعاد يجب أن يكون أيضًا دوريًا. لذلك ، على سبيل المثال ، حسب الإنشاء ، فإن الشروط الأولية على الأقل ليست دورية ، وبالتالي لا يمكن أن يكون كلا العمودين دوريًا. العبارة نفسها صحيحة إذا لم تكن الأعمدة متجاورة ، وإذا كانت جميع الخلايا في كلا العمودين غير معروفة. ومع ذلك ، لا توجد طريقة معروفة لتوزيع هذا الحكم على عمود واحد ، مثل العمود المركزي ، وبالتالي فإنه لا يحل المهمة الأولى للمنافسة بموجب المادة 30.
لذا ، ما الذي يمكن استخدامه لحلها؟ إذا اتضح أن العمود المركزي دوري في النهاية ، يمكنك فقط حسابه. نحن نعلم أنه ليس دوريًا بالنسبة للمليارات من الخطوات الأولى ، لكن يمكننا على الأقل افتراض وجود عملية انتقالية تتضمن تريليونات من الخطوات ، وبعد ذلك تصبح دورية.
هل تعتقد أن هذا أمر معقول؟
يحدث العبور - ومن الناحية النظرية (كما في
المشكلة الكلاسيكية
المتمثلة في إيقاف تشغيل آلة Turing ) ، يمكن أن تكون ذات طول تعسفي. هنا نلقي نظرة على بعض الأمثلة - وجدت أثناء البحث -
قواعد مع 4 ألوان ممكنة (الكود الشائع 150898). لنفترض أننا شغله 200 خطوة ، وكما ترى ، سيكون العمود المركزي عشوائيًا تمامًا:

قانونArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {200, 150 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]},
PixelConstrained -> 2, Frame -> False]
بعد 500 خطوة ، يبدو القالب بأكمله عشوائيًا تمامًا:

قانونArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {500, 300 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, Frame -> False,
ImagePadding -> 0, PlotRangePadding -> 0, PixelConstrained -> 1]
هنا يمكنك أن ترى أنه عند الاقتراب من العمود المركزي ، يحدث شيء مفاجئ: بعد 251 خطوة ، يبدو أن العمود المركزي قد تولد من جديد إلى قيمة ثابتة (أو على الأقل ثابت إلى أكثر من مليون خطوة التالية):

قانونGrid[{ArrayPlot[#, Mesh -> True,
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, ImageSize -> 38,
MeshStyle -> Lighter[GrayLevel[.5, .65], .45]] & /@
Partition[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {1400, {-4, 4}}],
100]}, Spacings -> .35]
هل يمكن أن يحدث نفس الانتقال في المادة 30؟ النظر في الأنماط من المادة 30 ، وحدد تلك التي تكون فيها الأقطار على اليسار دورية:

قانونsteps = 500;
diagonalsofrule30 =
Reverse /@
Transpose[
MapIndexed[RotateLeft[#1, (steps + 1) - #2[[1]]] &,
CellularAutomaton[30, {{1}, 0}, steps]]];
diagonaldataofrule30 =
Table[With[{split =
Split[Partition[Drop[diagonalsofrule30[[k]], 1], 8]],
ones = Flatten[
Position[Reverse[Drop[diagonalsofrule30[[k]], 1]],
1]]}, {Length[split[[1]]], split[[1, 1]],
If[Length[split] > 1, split[[2, 1]],
Length[diagonalsofrule30[[k]]] - Floor[k/2]]}], {k, 1,
2 steps + 1}];
transientdiagonalrule30 = %;
transitionpointofrule30 =
If[IntegerQ[#[[3]]], #[[3]],
If[#[[1]] > 1,
8 #[[1]] + Count[Split[#[[2]] - #[[3]]][[1]], 0] + 1, 0] ] & /@
diagonaldataofrule30;
decreasingtransitionpointofrule30 =
Append[Min /@ Partition[transitionpointofrule30, 2, 1], 0];
transitioneddiagonalsofrule30 =
Table[Join[
Take[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]] + 2,
Drop[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]]], {n, 1, 2 steps + 1}];
transientdiagonalrule30 =
MapIndexed[RotateRight[#1, (steps + 1) - #2[[1]]] &,
Transpose[Reverse /@ transitioneddiagonalsofrule30]];
smallertransientdiagonalrule30 =
Take[#, {225, 775}] & /@ Take[transientdiagonalrule30, 275];
Framed[ArrayPlot[smallertransientdiagonalrule30,
ColorRules -> {0 -> White, 1 -> Gray, 2 -> Hue[0.14, 0.55, 1],
3 -> Hue[0.07, 1, 1]}, PixelConstrained -> 1,
Frame -> None,
ImagePadding -> 0, ImageMargins -> 0,
PlotRangePadding -> 0, PlotRangePadding -> Full
], FrameMargins -> 0, FrameStyle -> GrayLevel[.75]]
على ما يبدو ، هناك حدود تفصل الترتيب إلى يسار الاضطراب إلى اليمين. وعلى الأقل بالنسبة لأول 100000 خطوة أو نحو ذلك ، يبدو أن الحدود تتغير في المتوسط بنحو 0.252 خطوة إلى اليسار في كل خطوة -
مع بعض الانحرافات العشوائية :
قانونdata = CloudGet[
CloudObject[
"https://www.wolframcloud.com/obj/bc470188-f629-4497-965d-\
a10fe057e2fd"]];
ListLinePlot[
MapIndexed[{First[#2], -# - .252 First[#2]} &,
Module[{m = -1, w},
w = If[First[#] > m, m = First[#], m] & /@ data[[1]]; m = 1;
Table[While[w[[m]] < i, m++]; m - i, {i, 100000}]]],
Filling -> Axis, AspectRatio -> 1/4, MaxPlotPoints -> 10000,
Frame -> True, PlotRangePadding -> 0, AxesOrigin -> {Automatic, 0},
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
لكن كيف اكتشفنا في النهاية عند أي نقطة ستتوقف هذه التقلبات عن كونها مهمة ، لدرجة أنها تفرض الأمر على اليسار لعبور العمود الأوسط ، وربما جعل القالب بأكمله دوريًا؟ استنادا إلى البيانات المتاحة ، يبدو الافتراض غير مرجح ، في حين لا يمكنني أن أقول بالضبط كيف يمكن تحديد ذلك.
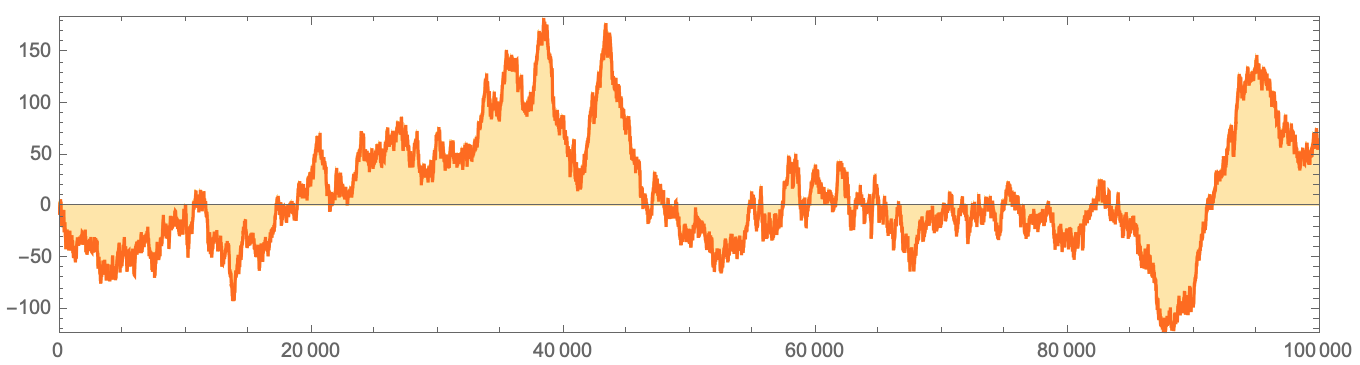
هذا ، بالطبع ، هو بالتحديد الحالة التي توضح وجود أنظمة ذات "عابرين" طويلة بشكل استثنائي. الآن النظر في توزيع الأعداد الأولية وحساب
LogIntegral [
n ] -
PrimePi [
n ]
قانونDiscretePlot[LogIntegral[n] - PrimePi[n], {n, 10000},
Filling -> Axis,
Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4,
Joined -> True, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
نعم ، هناك تقلبات ، ولكن في هذا الرسم التوضيحي يبدو أن هذا الاختلاف سيكون دائمًا في المجال الإيجابي. وهذا ، على سبيل المثال ، هو ما كان يناقشه رامانوجان ، ولكن في النهاية
اتضح أن هذا ليس كذلك . في البداية ، كانت حدود المكان الذي فشل فيه كبيرة في ذلك الوقت (
عدد Skives 10
10 10 964 ). وعلى الرغم من أن أحداً لم يجد بعد قيمة واضحة لـ
n والتي يكون الفارق سالبًا بها ، فمن المعروف أنه يجب أن يوجد
n = 10
317 (وفي النهاية سيكون الفرق سالبًا).
لقد شكلت الرأي القائل بأنه لا يوجد شيء من هذا القبيل يحدث في العمود المركزي من المادة 30 ، ولكن حتى الآن ليس لدينا دليل على أن هذا مستحيل ، لا يمكن المجادلة.
تجدر الإشارة إلى أنه من الممكن أن نفترض أنه على الرغم من أنه من الممكن بشكل أساسي إثبات الدورية من خلال الكشف عن الانتظام في العمود المركزي من المادة 30 ، لا يمكن القيام بأي شيء من هذا القبيل لغير الدورية. من المعروف أن هناك أنماطًا تكون أعمدةها المركزية غير دورية ، على الرغم من أنها منتظمة جدًا. الفئة الرئيسية من هذه الأمثلة هي قوالب متداخلة. هنا ، على سبيل المثال ، مثال بسيط للغاية من القاعدة 161 ، حيث يحتوي العمود الأوسط على خلايا بيضاء عند
n = 2
k :

قانونGraphicsRow[
ArrayPlot[CellularAutomaton[161, {{1}, 0}, #]] & /@ {40, 200}]
وهنا
مثال أكثر تعقيدًا قليلاً (من القاعدة 69540422 ذات اللونين لجارين) ، حيث يكون العمود المركزي هو
تسلسل Thue - Morse -
ThueMorse [
n ]:

قانونGraphicsRow[
ArrayPlot[
CellularAutomaton[{69540422, 2, 2}, {{1},
0}, {#, {-#, #}}]] & /@ {40, 400}]
يمكننا أن نفترض أن تسلسل Thue - Morse يتم إنشاؤه بواسطة التطبيق المتسلسل للاستبدال:

قانونRulePlot[SubstitutionSystem[{0 -> {0, 1}, 1 -> {1, 0}}],
Appearance -> "Arrow"]
اتضح أنه تم تعيين المصطلح
nth في هذا التسلسل على أنه
Mod [
DigitCount [
n ، 2، 1]، 2] - لن يكون هذا الكائن دوريًا أبدًا.
هل يمكن أن يكون العمود المركزي للقاعدة 30 من خلال
الاستبدال ؟ إذا كان الأمر كذلك ، فسأندهش من هذه الحقيقة (على الرغم من أنه
يبدو أن هناك أمثلة طبيعية عند ظهور أنظمة إحلال معقدة للغاية ) ، لكن مرة أخرى ، طالما لا يوجد دليل على ذلك.
تجدر الإشارة إلى أن جميع المهام التنافسية من المادة 30 يتم أخذها في الاعتبار عند صياغة خوارزمية تعمل على عدد لا حصر له من الخلايا. ,
n , , ( )? , 2
n —
, , .
n =5:

Graph[# -> CellularAutomaton[30][#] & /@ Tuples[{1, 0}, 4],
VertexLabels -> ((# ->
ArrayPlot[{#}, ImageSize -> 30, Mesh -> True]) & /@
Tuples[{1, 0}, 4])]
=5
n =11:

Row[Table[
Framed[Graph[# -> CellularAutomaton[30][#] & /@
Tuples[{1, 0}, n]]], {n, 4, 11}]]
, , , , . , 2
n ( , ,
).
,
n 30 ,
, 2 n .
, ( ):
ListLogPlot[
Normal[Values[
ResourceData[
"Repetition Periods for Elementary Cellular Automata"][
Select[#Rule == 30 &]][All, "RepetitionPeriods"]]],
Joined -> True, Filling -> Bottom, Mesh -> All,
MeshStyle -> PointSize[.008], AspectRatio -> 1/3, Frame -> True,
PlotRange -> {{47, 2}, {0, 10^10}}, PlotRangePadding -> .1,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
, ,
n 2
0.63 n . , , . , , ? .
2: ?
10000 30:
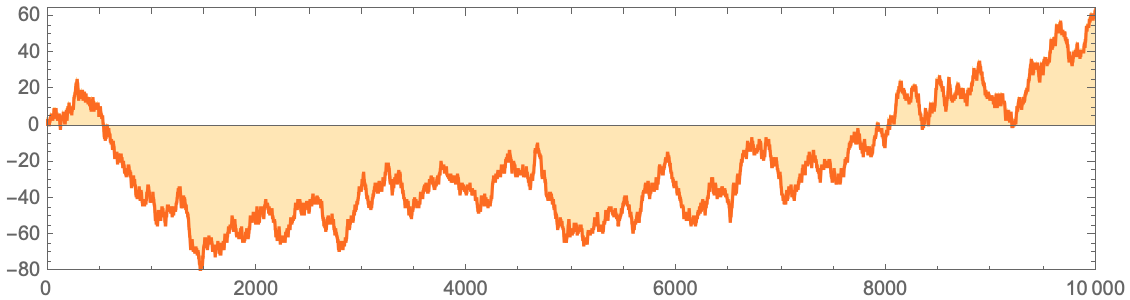
RListLinePlot[
Accumulate[2 CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}] - 1],
AspectRatio -> 1/4, Frame -> True, PlotRangePadding -> 0,
AxesOrigin -> {Automatic, 0}, Filling -> Axis,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
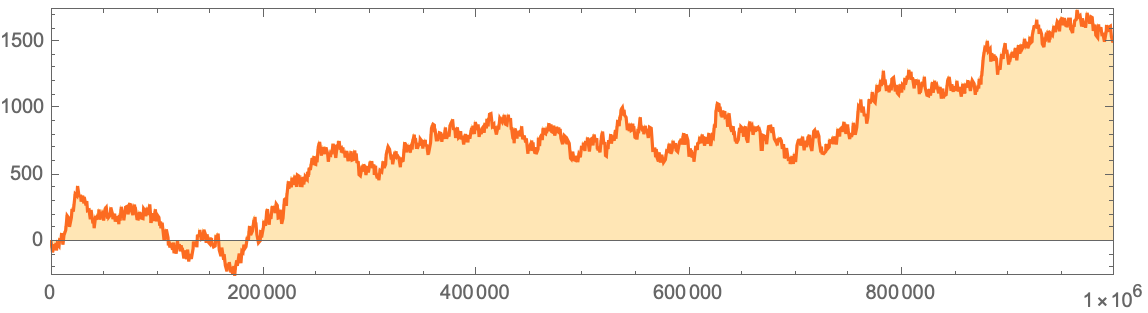
ListLinePlot[
Accumulate[
2 ResourceData[
"A Million Bits of the Center Column of the Rule 30 Cellular Automaton"] - 1], Filling -> Axis, Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4, MaxPlotPoints -> 1000, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
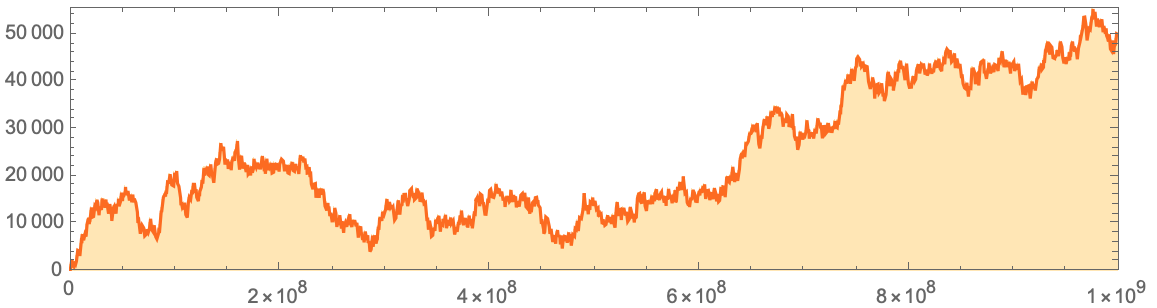
data=Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]];
data=Accumulate[2 data-1];
sdata=Downsample[data,10^5];
ListLinePlot[Transpose[{Range[10000] 10^5,sdata}],Filling->Axis,Frame->True,PlotRangePadding->0,AspectRatio->1/4,MaxPlotPoints->1000,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, , 1 () 0 (), , , , , , , .
. 10 000 :

Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.88, 1.04}}]]
, 1? …
, :
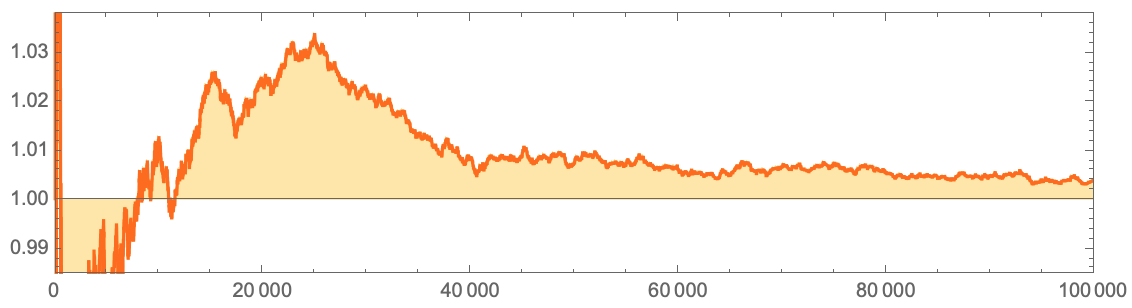
Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^5 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.985, 1.038}}]]
, , . 1 , :
accdata=Accumulate[Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]]];
diffratio=FunctionCompile[Function[Typed[arg,TypeSpecifier["PackedArray"]["MachineInteger",1]],MapIndexed[Abs[N[#]/(First[#2]-N[#])-1.]&,arg]]];
data=diffratio[accdata];
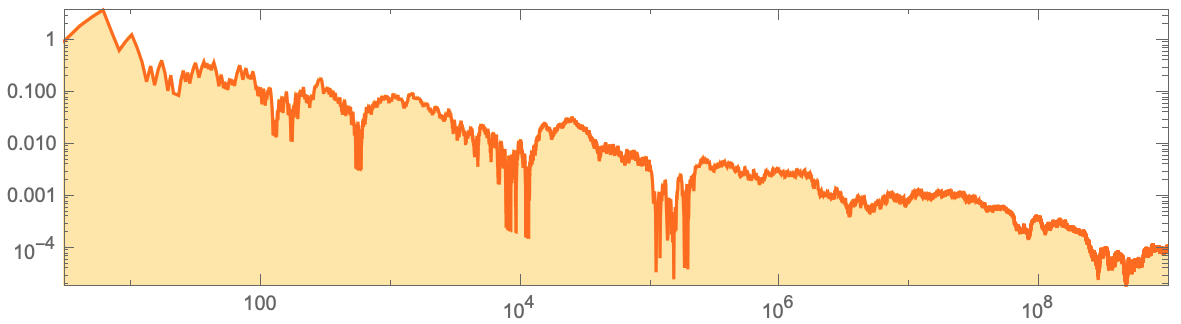
ListLogLogPlot[Join[Transpose[{Range[3,10^5],data[[3;;10^5]]}],Transpose[{Range[10^5+1000,10^9,1000],data[[10^5+1000;;10^9;;1000]]}]],Joined->True,AspectRatio->1/4,Frame->True,Filling->Axis,PlotRangePadding->0,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, ? . , . , , , , .
, , 30, .
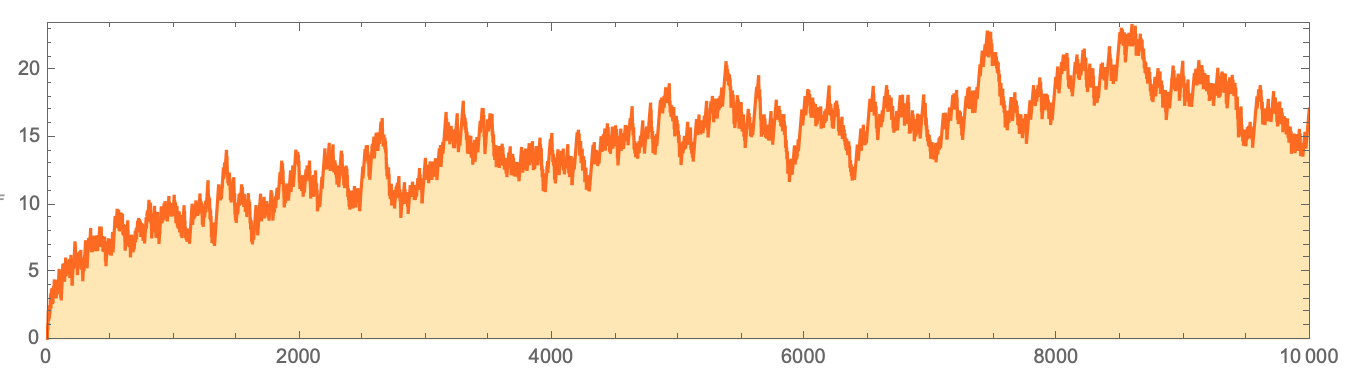
, ,
k . , 2
k . , - , , , , 30
k ( ).
,
. , ,
k =22, 2
k , , :

ListLogPlot[{3, 7, 13, 63, 116, 417, 1223, 1584, 2864, 5640, 23653,
42749, 78553, 143591, 377556, 720327, 1569318, 3367130, 7309616,
14383312, 32139368, 58671803}, Joined -> True, AspectRatio -> 1/4,
Frame -> True, Mesh -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.01]}],
PlotTheme -> "Detailed",
PlotStyle -> Directive[{Thickness[.004], Hue[0.1, 1, 0.99]}]]
, , . , –
, , .
—
— , , ,
, , , 30,
, ,
, , .
30 , , «
», , , , , , . , «»: 30, , , , , , , , 30.
, . 30, , - ,
, , 30, , , - .
. 30
, , . , , 30 - ( ), , , , 30. 200 :

ListLinePlot[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {200, {0, 200}}], Mesh -> All,
AspectRatio -> 1/4, Frame -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.0085]}],
PlotTheme -> "Detailed", PlotStyle -> Directive[{
Hue[0.1, 1, 0.99]}], ImageSize -> 575]
, :

Grid[{Table[
Histogram[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {10^n, {0, 20}}], {.01},
Frame -> True,
FrameTicks -> {{None,
None}, {{{0, "0"}, .2, .4, .6, .8, {1, "1"}}, None}},
PlotLabel -> (StringTemplate["`` steps"][10^n]),
ChartStyle -> Directive[Opacity[.5], Hue[0.09, 1, 1]],
ImageSize -> 208,
PlotRangePadding -> {{0, 0}, {0, Scaled[.06]}}], {n, 4, 6}]},
Spacings -> .2]
, , , 0 1.
1900- . , ,
FractionalPart [
hn ]
n h . ,
FractionalPart [
h n ]
h (
), —
FractionalPart [(3/2)
n ] — . (,
, 16- , , 2-
FractionalPart [16
x n -1 +
r [
n ]],
r [
n ]
n .)
3: n- O( n ) ?
,
150 :

Row[{ArrayPlot[CellularAutomaton[150, {{1}, 0}, 30], Mesh -> All,
ImageSize -> 315],
ArrayPlot[CellularAutomaton[150, {{1}, 0}, 200], ImageSize -> 300]}]
, ( ), , :

ArrayPlot[{Table[Mod[IntegerExponent[t, 2], 2], {t, 80}]},
Mesh -> All, ImageSize -> Full]
? , ,
:
Mod [
IntegerExponent [
n , 2], 2]. ,
n , , .
, « »? ,
n ,
Log [2,
n ] . , , O(log
n ) .
- 30? ,
n- , 30
n 2 , , . , -, , , — , , , , , .
« » (,
, . .), , , , , (,
,
3D- . .), .
,
1980- , , , ,
, , , .
, 3 30 , , . ( O(
n ) ; O(
n α ) α <2, , , O(log
β (
n )) — , , .)
3 , ,
n- , O(
n ), 150 .
O (
n )? () , « »?
, — — , , .
,
. , , ,
n , ,
,
n , (, «», O(log
n ) .
, . , , , ,
Wolfram Language . « ». , , Wolfram Language
, .
, 30 , 3 , , , , , ,
n- , O(
n ) , .
, , . , ,
. , , , , , — , O(log
n ) ,
n .
,
P NP . , 30 ( P
LOGTIME ), , , , . , , ,
n n , O(
n 2 ) , , P (« »), , , , , NP. («») , , , , 2
n .
, 2
n , , . ,
NP- , , , NP . 30 NP-? , , ( - , 30
NP).
30 . : 30 , , 30, «» , , , , .
, 256
110 ( , ),
110 , ,
, . , , , «» 110 .

SeedRandom[23542345]; ArrayPlot[
CellularAutomaton[110, RandomInteger[1, 600], 400],
PixelConstrained -> 1]
30, , — , «» , . ,
, 30 , , ,
, .
, , , , , 30. , , (, )
, , . , , — , . , .
, , 3.
,
,
,
,
n- ?
, 30 . , 2
m 2 m ×
m , , . , , , O(
n 2 ) ( ). , O(
n ) ? .
, 1 , , - O(
n ) — , « ». , ( , 2 ), , , .
- , , , ? ,
, .
. «» , , , .
30 - . ( — — 30
Wolfram Language, « !» ).
: «
- , , ». ? , , , - .
. , — , . ,
, , — - «» 30.
,
30. , 30 - . , , , - 30 , , , , — 30, , , , .
. ,
3 2 6 :

Row[Riffle[
ArrayPlot[#, ImageSize -> {Automatic, 275}] & /@ {Table[
IntegerDigits[3^t, 2, 159], {t, 100}],
Table[IntegerDigits[3^t, 6, 62], {t, 100}]}, Spacer[10]]]
, 6
. ( 2 ). , , .
s- n .
s- 3
n , «» (
b — , 2 6)
Mod [
Quotient [3
n , b
s ], b]. ? , 3
n n , : , , 3
n , log(
n ). , ,
, . , 30, , - , .
3
n -
30 , , O(
n ), ,
n , . ,
r [
n ] ,
r [
n ] «O-»
n , ,
MaxLimit [
r [
n ]/
n ,
n →∞ ]<∞.
, ( - ), . ,
r [
n ]
n , , , - , ,
r [
n ]
. , -
n ( - ),
r [
n ] . , , ,
r [
n ] O(
n ).
30
, ( , ).
Wolfram Language
t 30 :
![c[t_] c[t_]](https://habrastorage.org/getpro/habr/post_images/219/e07/f8e/219e07f8ec41111ce3457989e3d3c188.png)
c[t_] := CellularAutomaton[30, {{1}, 0}, {t, {{0}}}]
[
t ].
1: ?

\!\(
\*SubscriptBox[\(\[NotExists]\), \({p, i}\)]\(
\*SubscriptBox[\(\[ForAll]\), \(t, t > i\)]c[t + p] == c[t]\)\)

NotExists[{p, i}, ForAll[t, t > i, c[t + p] == c[t]]]
,
t >
i ,
[
t +
p ]
c [
t ].
2: ?

\!\(\*UnderscriptBox[\(\[Limit]\), \(t\*
UnderscriptBox["\[Rule]",
TemplateBox[{},
"Integers"]]\[Infinity]\)]\) Total[c[t]]/t == 1/2

DiscreteLimit[Total[c[t]]/t, t -> Infinity] == 1/2
[
t ]/
t t →∞ 1/2.
3: n- O( n ) ?
machine[
m ] ,
m (,
TuringMachine [...]), machine[
m ][
n ] {
v ,
t },
v — ,
t — (, ). :
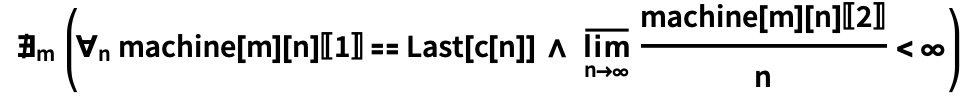
\!\(
\*SubscriptBox[\(\[NotExists]\), \(m\)]\((
\*SubscriptBox[\(\[ForAll]\), \(n\)]\(\(machine[m]\)[n]\)[[1]] ==
Last[c[n]]\ \[And] \
\*UnderscriptBox[\(\[MaxLimit]\), \(n -> \[Infinity]\)]
\*FractionBox[\(\(\(machine[m]\)[n]\)[[
2]]\), \(n\)] < \[Infinity])\)\)
« m, , machine[
m ]
n c [
n ] ,
n , ». (
m , «» ).
, , , , . 3 ( ), , 1 2, . 3 ( ), , 1 . :
1 , , 3 .
1 , , , , , 2. , 2 - 3. ,
, O(
n ) — , , 3, , .
, , ?
1 , , , 30 - , . , 1 , . , , - , .
( , ), 2, 3 , — , , , . , 3 , , (, , ), O(
n ) .
, - . ,
n n- . . , - , . , ,
n n . , . , « » . ,
n , . , , O(
n ) .
:
? « »,
/
( ).
, , (
)? , , , , «» , -, ( ) , .
, ,
. , , , . , () .
, , , , : «
». , , , .
, — - . -
n , . . — («
» . .). , , , .
— , , . , (
FindEquationalProof ). , ()
.
,
, , — , . — , .
, .
Wolfram|Alpha (, ) , . , .
, , -
, , , , .
? ,
«» , .
Wolfram Language , . Wolfram Language, .
« »? , , - . . - , , «» , , - ( ), . , , «» — , .
?
, ? . . , . - , . . - , , .
, , «» — , — , « ». ,
2,3 2007 .
— , , 30, , .
. - ( , , ). , , ( ) , , .
n — 30
n ,
n .
Wolfram Language . , 0,4 100 000 :

CellularAutomaton[30, {{1}, 0}, {100000, {{0}}}]; // Timing
,
30 Xor [
p ,
Or [
q ,
r ]],
.
,
CellularAutomaton :

Module[{a = 1},
Table[BitGet[a, a = BitXor[a, BitOr[2 a, 4 a]]; i - 1], {i,
100000}]]; // Timing
.
. , , 30, , 30 , , , : .
. , , «»
. 30 — . , , , .
— , , . , , 30, .
, , 30,
. 45° , 30, , . ; . ?
? ? - ?
, , , , , .
?
30, . , , ,
, ,
. , - , , ,
, , , - .
– , «» .
( , - ). , , , ,
« » :

GraphicsRow[(ArrayPlot[
CellularAutomaton[30,
MapAt[1 - #1 &, Flatten[Table[#1, Round[150/Length[#1]]]], 50],
100]] &) /@ {{1, 0}, {1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0}, {1,
0, 0, 0, 0, 0, 0}, {1, 1, 1, 0, 0}}]
, , , . ? , « » ?
, (, ), , - 30?
« 30». , «» ? 30 , ? «» ?
, , 30, , , , 30, . 256 ( ) , , :

Row[Riffle[
Labeled[ArrayPlot[CellularAutomaton[#, {{1}, 0}, {150, All}],
PixelConstrained -> 1, Frame -> False],
Style[Text[StringTemplate["rule ``"][#]], 12],
LabelStyle -> Opacity[.5]] & /@ {45, 73}, Spacer[8]]]
, . , . ,
, . , , , « 30», .
« 30». 30 ( 1), , — , .
2, 30, , .
3 .
n- O(
n γ ) γ <2 ( - )? ,
n- , O(log(
n )) ? O(log(
n )) ? ? . ?
, 30. 30, (, , 110) , 30.
, NP-, 30 , , NP-? , . , , , « », 30?
?
2007 2,3 , — , , , . , . 30? . 40 , - ( , !). , , (, ) .
, - ( ), , , , , , , . ( ), , , .
, « » ( , ), . , . , (« » . .). . , - « », , , …
, . , , . , , . , .
, 30 40 , - .
Wolfram Language?
« Wolfram » ( ).