
في المقالة ، بالتفصيل ، وصولاً إلى أصغر التفاصيل ، يتم النظر في ثلاث طرق لأخذ Euler-Poisson متكاملة. في إحدى الطرق ، يتم اشتقاق صيغة تخفيض مساعدة. للعثور على بعض التكاملات المعقدة ، يمكن استخدام صيغ الاختزال التي تسمح لأحدها بتخفيض درجة التكامل وحساب التكاملات المقابلة في عدد محدود من الخطوات.
هذا التكامل مأخوذ من الوظيفة الغوسية:
I= int limit 0inftye−x2dxهناك طريقة رياضية مثيرة جدا للاهتمام. للعثور على التكامل الأصلي ، ابحث أولاً عن مربع هذا التكامل ، ثم اخذ الجذر من النتيجة. لماذا؟ نعم ، لأنه من الأسهل وغير المؤلم الذهاب إلى الإحداثيات القطبية. لذلك ، ضع في اعتبارك مربع التكامل الغوسي:
I2= int limit 0inftye−x2dx int limit 0inftye−y2dy= int limit 0infty int limit 0inftye− left(x2+y2 right)dxdyنرى أننا نحصل على جزء لا يتجزأ من بعض الوظائف
g left(x،y right)= exp left[− left(x2+y2 right) right] . في نهاية هذا السطح المتكامل ، يوجد عنصر المساحة في نظام الإحداثيات الديكارتية
dS=$dxd .
الآن دعنا ننتقل إلى نظام الإحداثيات القطبية:
startarrayldS=dxdy=rd varphi cdotdr left. تبدأarraylx=r cos varphiy=r sin varphi endarray right| tox2 cos2 varphi+y2 sin2 varphi=r2 tox2+y2=r2 endarray
هنا تجدر الإشارة إلى أن r يمكن أن تختلف من 0 إلى + because ، لأن تباينت x داخل نفس النطاق. لكن الزاوية φ تختلف من 0 إلى π / 2 ، والتي تصف منطقة التكامل في الربع الأول من نظام الإحداثيات الديكارتية. استبدال في المصدر ، نحصل على:
startarraylI2= int limit 0infty int limit 0inftye− left(x2+y2 right)dxdy= int limit frac pi20 int limit 0inftye−r2rd varphidr= int limit frac pi20d varphi int limit 0inftye−r2rdr= int limit frac pi20d varphi int limit 0inftye−r2 frac12d left(r2 right)== frac12 int limit frac pi20d varphi left( left.−e−r2 right| 0infty right)= frac12 int limit frac pi20d varphi left(−e− infty− left(−e0 right) right)= frac12 int limit frac pi20d varphi= frac12 left( left. varphi right| frac pi20 right)= frac pi4I2= frac pi4 toI= sqrt frac pi4= frac sqrt pi2 endarray
نظرًا لتماثل القيم المتكاملة والإيجابية لقيم integrand ، يمكننا استنتاج ذلك
int limit − inftyinftye−x2dx=2 int limit 0inftye−x2dx=2 cdot frac sqrt pi2= sqrt pi
دعنا نجد بعض الحلول أكثر؟ هذا مثير للاهتمام! :)
النظر في وظيفة
g left(t right)= left(1+t right)e−tالآن دعونا نتذكر الرياضيات المدرسية وإجراء دراسة بسيطة لوظيفة باستخدام المشتقات والحدود. لا يعني ذلك أننا سنضع حدودًا معقدة هنا (بعد كل شيء ، لن نجتازها في المدرسة) ، نحن نناقش فقط ما سيحدث للوظيفة إذا كانت حجتها تميل إلى الصفر أو إلى ما لا نهاية ، وبالتالي فإننا سوف نقدر السلوك غير المقارب ، وهو أمر مهم للغاية دائمًا في الرياضيات. هذا يشبه التقييم النوعي لما يحدث.
startarraylg left(t right)= left(1+t right)e−tg′ left(t right)=e−t− left(1+t right)e−t=−te−tg′ left(t right)=0 tot=0 left[ startarraylt<0 to−te−t>0 tog left(t right)− rmيزيدt>0 إلى−te−t<0 tog left(t right)− rmالنقص endarray right.g left(0 right)= left(1+0 right)e−0=1g left(−1 right)= left(1−1 right)e− left(−1 right)=0g left( infty right)= left(1+ infty right)e− infty=0 endarray
يحدها من قبل وحدة على الفاصل (-∞ ؛ + ∞) والصفر على الفاصل الزمني [-1 ؛ + ∞).
نجعل التغيير التالي للمتغيرات
t= pmx2ونحن نحصل على:
t = \ pm x ^ 2 \ إلى \ left \ {\ start {array} {l} 0 <\ left ({1 - x ^ 2} \ right) e ^ {x ^ 2} <1 \\ 0 < \ left ({1 + x ^ 2} \ right) e ^ {- x ^ 2} <1 \\ \ end {array} \ right. \ to \ left \ {\ start {array} {l} 0 <\ left ({1 - x ^ 2} \ right) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ right.
في حالة عدم المساواة الأولى ، نقوم بتقييد التباين (0،1) ، وفي الفترة الثانية ، الفاصل (0 ؛ + ∞) ، نرفع كلا من التباينات إلى القوة n ، نظرًا لأن أوجه عدم المساواة ذات المصطلحات الإيجابية يمكن رفعها إلى أي درجة إيجابية. نحصل على:
\ تبدأ {array} {* {20} c} {\ left \ {\ start {array} {l} \ left ({1 - x ^ 2} \ right) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ end {array} \ right.} & {\ Left \ {\ start {array} {l} e ^ {- nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} \\ x> 1 \\ \ end {array} \ right.} \\ \ end {array}
دعونا نبني رسومًا بيانية لـ n = 1 لإظهار عدم المساواة
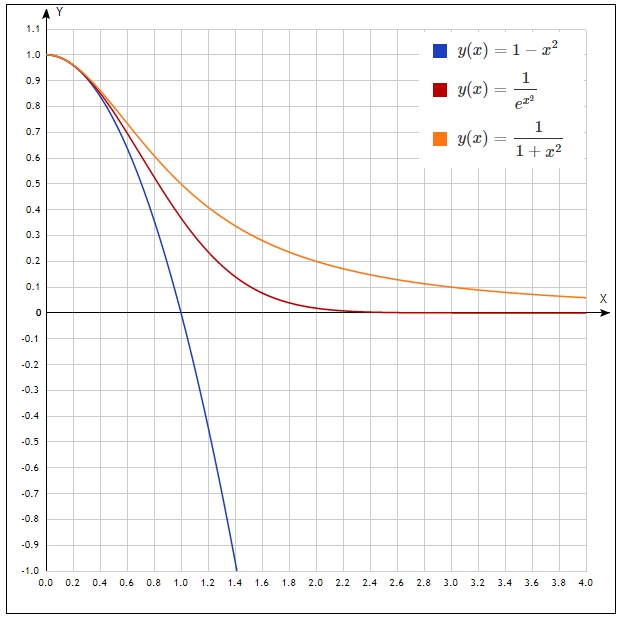
الآن نحاول دمج عدم المساواة ضمن الحدود المشار إليها في الأنظمة المقابلة. ودمج كل شيء على الفور في عدم مساواة واحدة:
int limit10 left(1−x2 right)ndx< int limit10e−nx2dx< int limit 0inftye−nx2dx< int limit 0infty frac1 left(1+x2 right)ndx
مرة أخرى ، إذا نظرت إلى الرسوم البيانية ، فإن عدم المساواة هذا صحيح.
بالنظر إلى بديل صغير ، فمن السهل أن نرى ما يلي:
int limit 0inftye−nx2dx= left[ startarraylp= sqrtnxp2=nx2 fracdp sqrtn=dx endarray right]= frac1 sqrtn int limit 0inftye−p2dp= frac1 sqrtnI
أي في هذا التباين الكبير في الوسط ، لدينا تكامل Euler-Poisson ، والآن نحن بحاجة إلى إيجاد التكاملات التي تقف على حدود هذا التفاوت.
العثور على لا يتجزأ من الحدود اليسرى:\ تبدأ {array} {l} \ int \ limit_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} = \ left [{\ start {array} {* {20} c} \ تبدأ {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} & \ ابدأ {array} {l} x = 1 \ to t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ to t = \ arcsin 0 = 0 \\ \ end {array} \\ \ end {array}} \ right] = \\ = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limit_0 ^ { \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {array}
من أجل حسابها وتقييمها ، دعونا أولاً نعثر على مكمل عام. الآن سأريكم كيفية اشتقاق صيغة التخفيض (في الرياضيات ، بمثل هذه الصيغ تعني تخفيض الدرجة) لتكامل معين.
\ start {array} {l} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cdot d \ left ({\ sin t} \ right)} = \\ = \ left [{\ start {array} {* { 20} c} {u = \ cos ^ {n - 1} t} & {du = - \ left ({n - 1} \ right) \ cos ^ {n - 2} t \ sin tdt} \\ {dv = d \ left ({\ sin t} \ right)} & {v = \ sin t} \\ \ end {array}} \ right] = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ left ({1 - \ cos ^ 2 t} \ right) dt} = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ left ({n - 1} \ right) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ end {array}
تبدأarrayl int limit alpha beta cosntdt= left. cosn−1t sint right| alpha beta+ left(n−1 right) int limit alpha beta cosn−2tdt− left(n−1 right) int limit alpha beta cosntdt int limit alpha beta cosntdt+ left(n−1 right) int limit alpha beta cosntdt= left. cosn−1t sint right| alpha beta+ left(n−1 right) int limit alpha beta cosn−2tdtn int limit alpha beta cosntdt= left. cosn−1t sint right| alpha beta+ left(n−1 right) int limit alpha beta cosn−2tdt int limit alpha beta cosntdt= frac1n left. cosn−1t sint right| alpha beta+ fracn−1n int limit alpha beta cosn−2tdt endarray
الآن ، إذا استخدمنا صيغة التخفيض ، فإننا نعتبرها جزءًا لا يتجزأ ، ولكن مع حدودنا من 0 إلى π / 2 ، يمكننا حينئذٍ إجراء بعض التبسيط:
\ start {array} {l} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ left [{\ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} = 0} \ right] = \\ = \ frac {{n - 1}} { n} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ left ({\ frac {1 } {{n - 2}} \ left. {\ cos ^ {n - 3} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \\ = \ frac {{n - 1 }} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5 }} {{n - 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ right) = \ right) = \\ = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5}} {{n - 4}} \ left ({\ frac {{n - 7}} {{n - 6}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} \ اليمين )} \ right)} \ right) = ... \\ \ end {array}
كما نرى ، يمكنك خفضه إلى ما لا نهاية (يعتمد على n). ومع ذلك ، هناك دقة واحدة. تتغير الصيغة اعتمادًا على ما إذا كان n هو رقم زوجي أم لا.
لهذا ، فإننا نعتبر حالتين.
تبدأarrayln=10: int limit frac pi20 cos10tdt= frac9 cdot7 cdot5 cdot310 cdot8 cdot6 cdot4 int limit frac pi20 cos2tdt= frac9 cdot7 cdot5 cdot310 cdot8 cdot6 cdot4 int limit frac pi20 left( frac12+ frac12 cos2t right)dt== frac9 cdot7 cdot5 cdot310 cdot8 cdot6 cdot4 left. left( frac12t+ frac12 sin2t right) right| frac pi20= frac9 cdot7 cdot5 cdot310 cdot8 cdot6 cdot4 cdot frac pi4= frac9 cdot7 cdot5 cdot3 cdot110 cdot8 cdot6 cdot4 cdot2 cdot frac pi2== frac left(n−1 right)!!n!! cdot frac pi2 endarray
تبدأarrayln=9: int limit frac pi20 cos9tdt= frac8 cdot6 cdot4 cdot29 cdot7 cdot5 cdot3 int limit frac pi20 costdt= frac8 cdot6 cdot4 cdot29 cdot7 cdot5 cdot3اليسار. left( sint right) right| frac pi20== frac8 cdot6 cdot4 cdot29 cdot7 cdot5 cdot3 cdot1= frac left(n−1 right)!!n!! endarray
أين ن !! - مضروب مزدوج. يشار إلى مضروب مزدوج من ن! ويتم تعريفه على أنه ناتج جميع الأعداد الطبيعية في الفاصل الزمني [1 ، n] له نفس التكافؤ مثل n
نظرًا لحقيقة أن 2n + 1 هو رقم فردي لأي قيمة n ، فإننا نحصل على الحد الأيسر لعدم المساواة لدينا:
int limit frac pi20 cos2n+1tdt= frac left(2n right)!! left(2n+1 right)!!
العثور على لا يتجزأ من الحدود اليمنى:(هنا نستخدم نفس صيغة التخفيض التي أثبتت سابقًا)
startarrayl int limit 0infty frac1 left(1+x2 right)ndx= left[ startarraylx= tant to startarray∗20cx=0 tot=0x= infty tot= frac pi2 endarraydx= fracdt cos2t frac11+x2= frac11+ tan2t= cos2t endarray right]== int limit frac pi20 cos2n−2tdt= left[ left(2n−2 right)− rmevenإلىاليمين]= frac left(2n−3 right)!! left(2n−2 right)!! cdot frac pi2 endarray
بعد تقدير الجانبين الأيسر والأيمن من عدم المساواة ، نجري بعض التحولات لتقييم حدود الجانبين الأيسر والأيمن من عدم المساواة ، بشرط أن يميل n إلى:
startarrayl frac left(2n right)!! left(2n+1 right)!!< frac1 sqrtn cdotI< frac left(2n−3 right)!! left(2n−2 right)!! cdot frac pi2 sqrtn cdot frac left(2n right)!! left(2n+1 right)!!<I< sqrtn cdot frac left(2n−3 right)!! left(2n−2 right)!! cdot frac pi2 endarray
مربع جانبي عدم المساواة:
n cdot frac left( left(2n right)!! right)2 left( left(2n+1 right)!! right)2<I2<n cdot frac left( left(2n−3 right)!! right)2 left( left(2n−2 right)!! right)2 cdot frac pi24
الآن دعونا نفعل القليل من الاكتئاب. في عام 1655 ، اقترح جون واليس (عالم رياضيات إنجليزي ، أحد رواد التحليل الرياضي.) صيغة لتحديد الرقم π. جاء إلي واليس ، وحساب مساحة الدائرة. يتقارب هذا المنتج ببطء شديد ، وبالتالي فإن صيغة واليس لا تُستخدم إلا قليلاً في الحساب العملي للرقم π. ولكن من الرائع تقييم تعبيرنا :)
pi= mathop lim limitn to infty frac1n left[ frac left(2n right)!! left(2n−1 right)!! right]2
الآن نقوم بتحويل عدم المساواة لدينا حتى يمكننا أن نرى مكان استبدال صيغة واليس:
\ تبدأ {array} {l} \ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2} } <I ^ 2 <\ frac {1} {{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ right) ^ 2 }} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}}} \ اليمين] \ cdot \ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ اليمين ) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2}}} \ اليمين] <I ^ 2 <\ frac {1} {{\ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ يمين) ^ 2}} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}} \ right]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ \ frac {1} {4} \ cdot \ pi <I ^ 2 <\ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ to \ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}
يتبع من صيغة واليس أن تعبيرات اليسار واليمين تميل إلى π / 4 كـ n → ∞
نظرًا لحقيقة أن الدالة exp [-x²] متساوية ، فإننا نفترض ذلك بأمان
int limit − inftyinftye−x2dx=2 int limit 0inftye−x2dx=2 cdot frac sqrt pi2= sqrt pi
لأول مرة ، تم حساب التكامل الغوسي أحادي البعد في عام 1729 بواسطة Euler ، ثم وجد Poisson طريقة بسيطة لحسابه. في هذا الصدد ، كان يطلق عليه Euler - Poisson لا يتجزأ.
دعونا نحاول حساب التكامل الغوسي. يمكن كتابتها بأشكال مختلفة. بعد كل شيء ، لا شيء يغير اسم المتغير الذي يتم به التكامل.
تبدأarraylI= int limit 0inftye−x2dxI= int limit − inftyinftye−x2dx= int limit − inftyinftye−y2dy= int limit − inftyinftye−z2dz endarray
يمكنك الانتقال من الديكارتي ثلاثي الأبعاد إلى الإحداثيات الكروية والنظر في مكعب غاوس لا يتجزأ.
\ left \ {\ start {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {صفيف} \ اليمين. \ to x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2
يعقوبي من هذا التحول يمكن حسابها على النحو التالي:
\ تبدأ {array} {l} J = \ left | {\ start {array} {* {20} c} {\ frac {{\ جزئية x}} {{\ جزئية r}}} & {\ frac {{\ جزئية x}} {{\ جزئية \ theta}} } & {\ frac {{\ جزئية x}} {{\ جزئية \ varphi}}} \\ {\ frac {{\ جزئي y}} {{\ جزئية r}}} & {\ frac {{\ جزئية y }} {{\ جزئية \ theta}}} & {\ frac {{\ جزئي y}} {{\ جزئية \ varphi}}} \\ {\ frac {{\ جزئية ض}} {{\ جزئية r}} } & {\ frac {{\ جزئية ض}} {{\ جزئية \ ثيتا}}} & {\ frac {{\ جزئية ض}} {{\ جزئية \ varphi}}} \\ \ end {array}} \ الحق | = \ اليسار | {\ start {array} {* {20} c} {\ sin \ theta \ cos \ varphi} & {r \ cos \ theta \ cos \ varphi} & {- r \ sin \ theta \ sin \ varphi} \\ {\ sin \ theta \ sin \ varphi} & {r \ cos \ theta \ sin \ varphi} & {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} & {- r \ sin \ theta} & 0 \\ \ end {array}} \ right | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}
تبدأarraylI3= int limit − inftyinfty int limit − inftyinfty int limit − inftyinftye−x2−y2−z2dxdydz= int limit2 pi0 int limit 0pi int limit 0inftye−r2Jdrd thetad varphi== int limit2 pi0d varphi int limit 0pi sin thetad theta int limit 0inftye−r2r2dr endarray
نحسب التكاملات بالتسلسل ، بدءا من واحد الداخلي.
تبدأarrayl int limit 0inftye−r2r2dr= left[ startarraylu=r todu=drdv=re−r2dr tov= intre−r2dr= frac12 inte−r2dr2=− frac12e−r2 endarray right]== left. left(− frac12re−r2 right) right| 0infty+ frac12 int limit 0inftye−r2dr= frac12 int limit 0inftye−r2dr= frac12 cdot fracI2= fracI4 int limit 0pi sin thetad theta= left. left(− cos theta right) right| 0pi= left(− cos pi right)− left(− cos0 right)=1+1=2 int limit2 pi0d varphi= left. varphi right|2 pi0=2 pi endarray
ثم نتيجة لذلك نحصل على:
تبدأarraylI3=2 pi cdot2 cdot fracI4 إلىI3= piI toI2= pi toI= sqrt piI= int limit − inftyinftye−x2dx= sqrt pi endarray
غالبًا ما يستخدم تكامل Euler-Poisson في نظرية الاحتمالات.
آمل أن تكون هذه المادة مفيدة لشخص ما وتساعد على فهم بعض التقنيات الرياضية :)