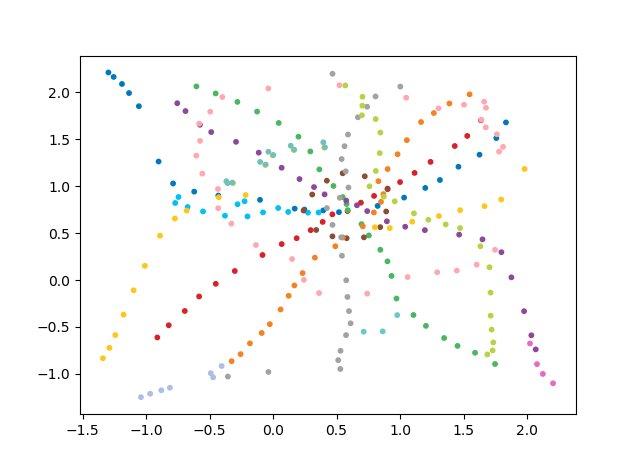
محدث: كما هو مطلوب في التعليقات ، أضفت رابطًا إلى مخطط جافا سكريبت الدوار
لسوء الحظ ، تعذر إدخال كود javascript في نص المنشور
مساء الخير لقد قرأت مؤخرًا مدونة لأحد سكان المدن كان يناقش الشكل الذي يجب أن يكون عليه مخطط المترو المثالي ، ويمكن رسم مخطط المترو على أساس مبدأين:
- يجب أن تكون الدائرة مريحة وسهلة التذكر والتوجيه.
- يجب أن يتوافق المخطط مع جغرافية المدينة
من الواضح أن هذه المبادئ تستبعد بعضها بعضًا ويتطلب المبدأ الأول تشويهًا ملموسًا للواقع الجغرافي.
يكفي أن نتذكر كيف يبدو مخطط مترو موسكو بحلقات جميلة وخطوط مستقيمة:
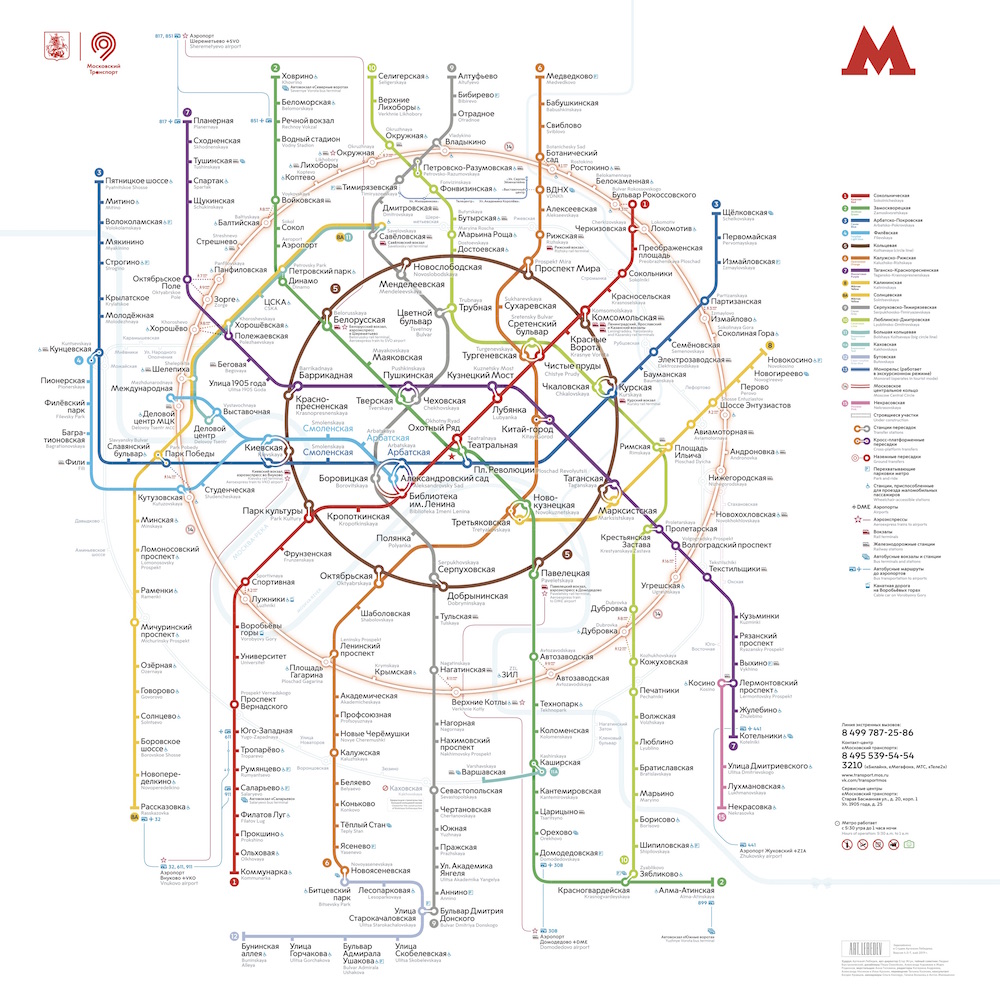
والمقارنة مع خطة دقيقة جغرافيا:

توضح الخطة أن الحلقات ليست سلسة ومركبة تمامًا على الإطلاق ، تنحني الخطوط كثيرًا عن المخطط ، وكثافة المحطات في وسط المدينة عالية جدًا لدرجة أنه من المستحيل تقريبًا تحديد الخطة.
على الرغم من أن الصورة الثانية تعكس الواقع بشكل أكثر دقة ، فمن الواضح أنه من الأنسب استخدام المخطط الأول للتخطيط لمسار في المترو.
ثم فكرت الفكرة التالية: "كيف سيبدو المترو إذا كان المعيار لبناء الدائرة هو الوقت اللازم للانتقال من محطة إلى أخرى؟" بمعنى أنه إذا استطعت الانتقال من محطة إلى أخرى بسرعة ، فسيكون موقعها قريبًا على الرسم التخطيطي.
من الواضح ، في الفضاء ثنائي الأبعاد ، من المستحيل رسم مثل هذا المخطط الذي تكون فيه المسافة بين محطتين مساوية لوقت السفر من محطة إلى أخرى بسبب الطوبولوجيا المعقدة للرسم البياني للمترو.
هناك أيضًا حدس بأن هذا ممكن تمامًا عند إنشاء مخطط في مساحة ذات بعد كبير (التقدير العلوي هو n-1 ، حيث n هو عدد المحطات). بالنسبة لمساحة ذات عدد صغير من الأبعاد ، لا يمكن بناء مثل هذا المخطط إلا تقريبًا.
تبدو مهمة إنشاء خريطة مترو بواسطة وقت السفر مهمة تحسين نموذجية.
افترض أن لدينا مجموعة أولية من الإحداثيات لجميع المحطات (X و Y و Z) ومصفوفة مستهدفة من الأوقات الزوجية (المسافات). من الممكن إنشاء مقياس "عدم صحة" لمجموعة معينة من الإحداثيات ومن ثم تقليلها باستخدام طريقة النسب التدرج لكل من إحداثيات كل محطة. كمقياس ، يمكننا القيام بوظيفة بسيطة للانحراف المعياري عن المسافات.
حسنًا ، الشيء الوحيد المتبقي هو الحصول على بيانات حول مقدار الوقت الذي يجب أن تقضيه في السفر من أي محطة لمترو موسكو إلى أي محطة أخرى.
كانت الفكرة الأولى هي التحقق من مؤشر مترو ياندكس والحصول على هذه البيانات من هناك. لسوء الحظ ، لا يمكن العثور على وصف api. شاهد الأوقات يدويًا في التطبيق لفترة طويلة (في المترو هناك 268 محطة وحجم المصفوفة الزمنية 268 * 268 = 71824). لذلك ، قررت أن أفهم البيانات المصدر لمترو ياندكس. نظرًا لعدم وجود إمكانية الوصول إلى الخادم ، تم تنزيل ملف apk مع التطبيق وتم العثور على البيانات اللازمة. جميع المعلومات حول المترو مبنية بشكل رائع وتخزينها في تنسيق JSON في مجلد أرشيف الأصول / metrokit / apk. يتم تخزين جميع البيانات في هياكل ذاتية الشرح. يحتوي Meta.json على معلومات حول المدن التي توجد مخططاتها في التطبيق ، بالإضافة إلى معرف هذه المخططات.
{ "id": "sc77792237", "name": { "en": "Nizhny Novgorod", "ru": " ", "tr": "Nizhny Novgorod", "uk": "і " }, "size": { "packed": 30300, "unpacked": 145408 }, "tags": [ "published" ], "aliases": [ "nizhny-novgorod" ], "logoUrl": "https://avatars.mds.yandex.net/get-bunker/135516/f2f0e33d8def90c56c189cfb57a8e6403b5a441c/orig", "version": "2c27fe1", "geoRegion": { "delta": { "lat": 0.168291, "lon": 0.219727 }, "center": { "lat": 56.326635, "lon": 43.992153 } }, "countryCode": "RU", "defaultAlias": "nizhny-novgorod" }
حسب معرف المخطط ، نجد المجلد مع JSON المتعلق بموسكو.
يحتوي ملف data.json على معلومات أساسية حول الرسم البياني للمترو ، بما في ذلك أسماء عقد الرسم البياني ، ومعرفات العقدة ، والإحداثيات الجغرافية للعقد ، ومعلومات حول الانتقال من محطة إلى أخرى (المعرف ، ووقت الانتقال ، ونوع الانتقال - سواء كانت القيادة أو المشي ، في الشارع أم لا ، الوقت نحن مهتمون بالثواني) وأيضًا الكثير من المعلومات الإضافية حول المداخل والمخارج من المحطة. هذا سهل بما فيه الكفاية لمعرفة. لنبدأ كتابة التعليمات البرمجية لبناء دائرتنا.
نستورد المكتبات اللازمة:
import numpy as np import json import codecs import networkx as nx import matplotlib.pyplot as plt import pandas as pd import itertools import keras import keras.backend as K from mpl_toolkits.mplot3d import Axes3D from mpl_toolkits.mplot3d.proj3d import proj_transform from matplotlib.text import Annotation import pickle
تتوافق بنية القواميس والقوائم بيثون تمامًا مع بنية تنسيق json ، لذلك نقرأ معلومات المترو وننشئ كائنات تتوافق مع كائنات json.
names = json.loads(codecs.open( "l10n.json", "r", "utf_8_sig" ).read() ) graph = json.loads(codecs.open( "data.json", "r", "utf_8_sig" ).read() )
ننشئ قاموسًا يعين عقد الرسم البياني والمحطة (يعد هذا ضروريًا لأن المحطات مخصصة للأسماء وليس للعقد البياني)
أيضا ، فقط في حالة ، سنقوم بحفظ إحداثيات العقد لإمكانية إنشاء خريطة جغرافية (تطبيع إلى مجموعة من 0-1)
nodeStdict={} for stop in graph['stops']['items']: nodeStdict[stop['nodeId']]=stop['stationId'] coordDict={} for node in graph['nodes']['items']: coordDict[node['id']]=(node['attributes']['geoPoint']['lon'],node['attributes']['geoPoint']['lat']) lats=[] longs=[] for value in coordDict.values(): lats.append(value[1]) longs.append(value[0]) for k,v in coordDict.items(): coordDict[k]=((v[0]-np.min(longs))/(np.max(longs)-np.min(longs)),(v[1]-np.min(lats))/(np.max(lats)-np.min(lats)))
إنشاء رسم بياني للمترو مع الاتصالات. وضعنا وزن كل اتصال. الوزن يتوافق مع وقت السفر. سنقوم بإزالة العقد التي ليست محطات (في رأيي ، هذه مخارج من المترو وهناك حاجة إلى اتصالات بها لبطاقات Yandex عند حساب الوقت ، لكن لم أفهمها بالضبط) ، قم بإنشاء قاموس معرف العقدة - الاسم الحقيقي باللغة الروسية
G=nx.Graph() for node in graph['nodes']['items']: G.add_node(node['id'])
نحدد الفرع (أي رقم الفرع) الذي تنتمي إليه كل عقدة (ستكون هناك حاجة إلى ذلك لاحقًا لتلوين خطوط المترو في المخطط)
def getlines(graph, G): nodetoline={} id_from={} id_to={} for lk in graph['tracks']['items']: id_from[lk['id']]=lk['fromNodeId'] id_to[lk['id']]=lk['toNodeId'] for line in graph['linesToTracks']['items']: if line['trackId'] in id_from.keys(): nodetoline[id_from[line['trackId']]]=line['lineId'] nodetoline[id_to[line['trackId']]]=line['lineId'] return nodetoline lines=getlines(graph,G)
تتيح لك مكتبة networkx العثور على أقصر طول المسار من عقدة إلى أخرى باستخدام وظيفة nx.shortest_path_length (G، id1، id2، weight = 'length') ، لذلك يمكننا افتراض أننا قد انتهينا من إعداد البيانات. الشيء التالي الذي يجب القيام به هو إعداد نموذج من شأنه تحسين إحداثيات المحطات.
للقيام بذلك ، سنعرف ما الذي سيتم إعطاؤه للمدخلات ، إلى المخرجات ، وكيف سنقوم بتحسين مصفوفة إحداثيات المحطة.
لنفترض أن لدينا مصفوفة لجميع الإحداثيات (3x268). ضرب متجه واحد ساخن (متجه حيث 0 في كل مكان باستثناء وحدة واحدة تحل محل n) من البعد 268 بواسطة هذه المصفوفة الإحداثية سيعطي 3 إحداثيات المقابلة للمحطة ن. إذا أخذنا زوجًا من المتجهات ذات درجة الحرارة الواحدة وضربناها في المصفوفة اللازمة ، فسنحصل على اثنين من الإحداثيات الثلاثية. من زوج من الإحداثيات يمكنك حساب المسافة الإقليدية بين المحطات. وبالتالي ، يمكننا تحديد بنية نموذجنا:
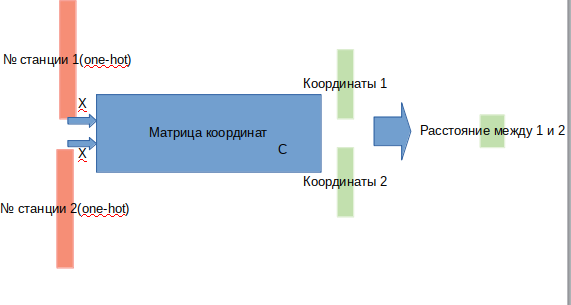
عند المدخل نعطي اثنين من المحطات ، في الإخراج نحصل على المسافة بينهما.
بعد أن نقرر تنسيق البيانات لتدريب النموذج ، سنقوم بإعداد البيانات باستخدام البحث عن بعد على الرسم البياني:
myIDs=list(G.nodes()) listofinputs1=[] listofinputs2=[] listofoutputs=[] for pair in itertools.product(G.nodes(), repeat=2): vec1=np.zeros((len(myIDs))) vec2=np.zeros((len(myIDs))) vec1[myIDs.index(pair[0])]=1 vec2[myIDs.index(pair[1])]=1 listofinputs1.append(vec1) listofinputs2.append(vec2)
نقوم بتحسين مصفوفة إحداثيات المحطة باستخدام طريقة النسب التدرج.
إذا استخدمنا إطار عمل keras للتعلم الآلي ، فسنحصل على ما يلي:
np.random.seed(0) initweightmatrix=np.zeros((len(myIDs),3)) for i in range(len(myIDs)): initweightmatrix[i,:2]=coordDict[myIDs[i]] initweightmatrix[i,2]=np.random.randn()*0.001 def euclidean_distance(vects): x, y = vects sum_square = K.sum(K.square(x - y), axis=1, keepdims=True) return K.sqrt(K.maximum(sum_square, K.epsilon())) def eucl_dist_output_shape(shapes): shape1, shape2 = shapes return (shape1[0], 1) inp1=keras.layers.Input((len(myIDs),)) inp2=keras.layers.Input((len(myIDs),)) layer1=keras.layers.Dense(3,use_bias=None, activation=None) x1=layer1(inp1) x2=layer1(inp2) x=keras.layers.Lambda(euclidean_distance, output_shape=eucl_dist_output_shape)([x1, x2]) out=keras.layers.Dense(1,use_bias=None,activation=None)(x) model=keras.Model(inputs=[inp1,inp2],outputs=out) model.layers[2].set_weights([initweightmatrix]) model.layers[2].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse')
لاحظ أننا نستخدم الإحداثيات الجغرافية الحقيقية باعتبارها الإحداثيات الأولية في layer1 - وهذا ضروري حتى لا نقع في الحد الأدنى المحلي لوظيفة الانحراف المعياري. نحن نهيئ الإحداثي الثالث بإحداثيات غير صفرية للحصول على تدرج غير صفري (إذا كانت الخريطة في البداية مسطحة تمامًا ، فإن تحول أي محطة لأعلى أو لأسفل سيكون هو نفسه ، وبالتالي فإن التدرج يكون 0 ولن يتم تحسين z). يؤثر العنصر الأخير من نموذجنا (Dense (1)) في توسيع نطاق المخطط ليناسب الجدول الزمني.
سنقوم بقياس المسافة بالساعات ، وليس بالثواني ، نظرًا لأن طلبات المسافات تبلغ حوالي ساعة واحدة ، وللتدريب الأكثر فعالية للنموذج ، من المهم أن تكون جميع القيم (بيانات الإدخال ، والأوزان ، والأهداف) تقريبًا بنفس الترتيب من حيث الحجم. إذا كانت هذه القيم قريبة من 1 ، فيمكنك استخدام قيم الخطوات القياسية للتحسين (0.001-0.01).
يقوم model line.layers [2] .trainable = False بتجميد إحداثيات المحطات وفي المرحلة الأولى يتم تغيير معلمة واحدة - المقياس. بعد تحديد حجم مخططنا ، نقوم بإلغاء تجميد الإحداثيات وتحسينها بالفعل:
hist=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200) model.layers[2].trainable=True model.layers[-1].trainable=False model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse') hist2=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200)
نرى أننا نتغذى على جميع أزواج المحطات في وقت واحد ، عند الخروج من جميع المسافات ، والتحسين هو نزول تدرج كامل للدفعات (خطوة واحدة على جميع البيانات). وظيفة الخسارة في هذه الحالة هي الانحراف المعياري ، ويمكنك أن ترى أنه كان 0.015 في نهاية التدريب ، مما يعني أن الانحراف المعياري أقل من دقيقة واحدة لأي زوج من المحطات. بمعنى آخر ، يتيح لك المخطط الناتج معرفة المسافة المطلوبة للانتقال من محطة إلى أخرى بدقة من خلال المسافة في خط مستقيم بين المحطات بدقة + -1 دقيقة!
ولكن دعونا نرى كيف تبدو دائرتنا!
احصل على إحداثيات المحطات ، خذ الترميز اللوني للخطوط وقم بإنشاء صورة ثلاثية الأبعاد بتوقيعات (يتم أخذ رمز العرض الجميل للتوقيعات
من هنا ):
class Annotation3D(Annotation): '''Annotate the point xyz with text s''' def __init__(self, s, xyz, *args, **kwargs): Annotation.__init__(self,s, xy=(0,0), *args, **kwargs) self._verts3d = xyz def draw(self, renderer): xs3d, ys3d, zs3d = self._verts3d xs, ys, zs = proj_transform(xs3d, ys3d, zs3d, renderer.M) self.xy=(xs,ys) Annotation.draw(self, renderer) def annotate3D(ax, s, *args, **kwargs): '''add anotation text s to to Axes3d ax''' tag = Annotation3D(s, *args, **kwargs) ax.add_artist(tag) fincoords=model.layers[2].get_weights() ccode={} for obj in graph['services']['items']: ccode[obj['id']]=('\#'+obj['attributes']['color'])[1:] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') for j, xyz_ in enumerate(xyzn): annotate3D(ax, s=labels[myIDs[j]], xyz=xyz_, fontsize=9, xytext=(-3,3), textcoords='offset points', ha='right',va='bottom') plt.show()
نظرًا لوجود صعوبات في التحويل إلى تنسيق ثلاثي الأبعاد تفاعلي للمتصفح ، أقوم بنشر ملفات gif:
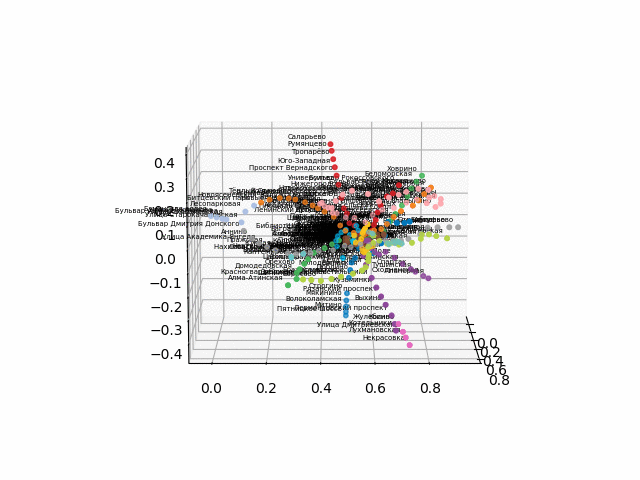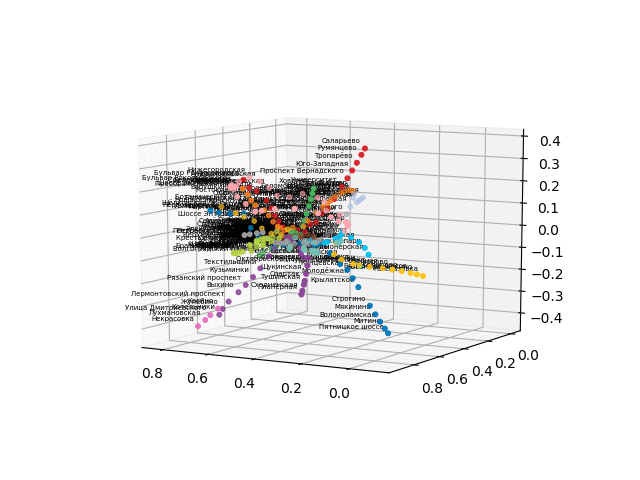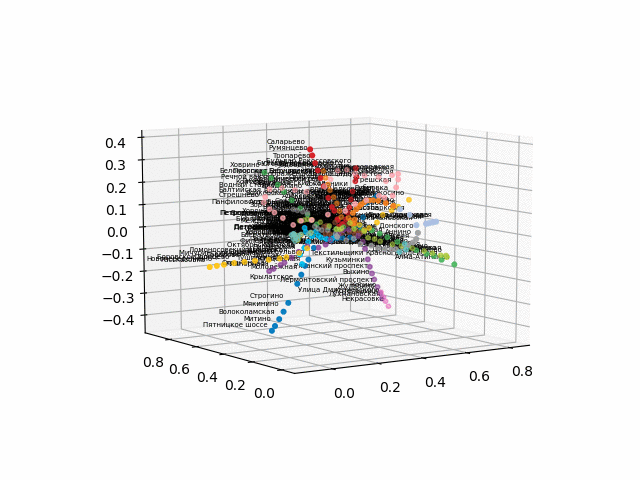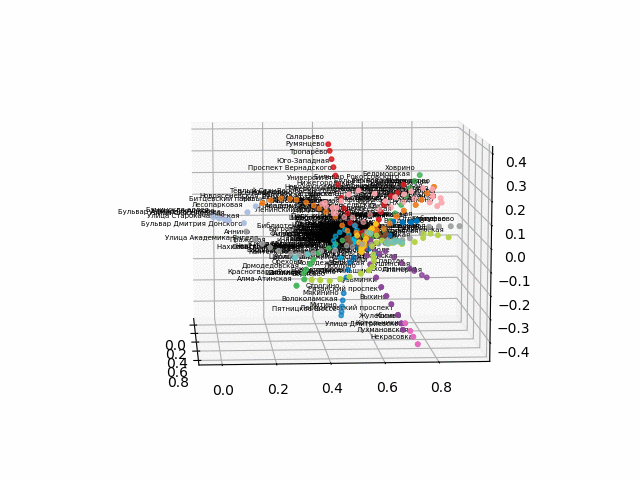
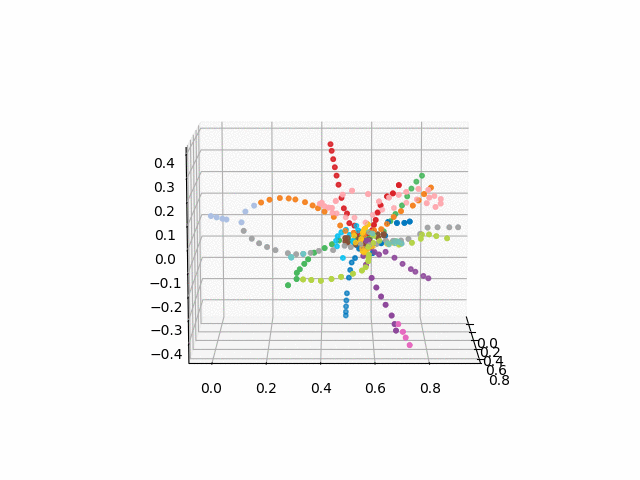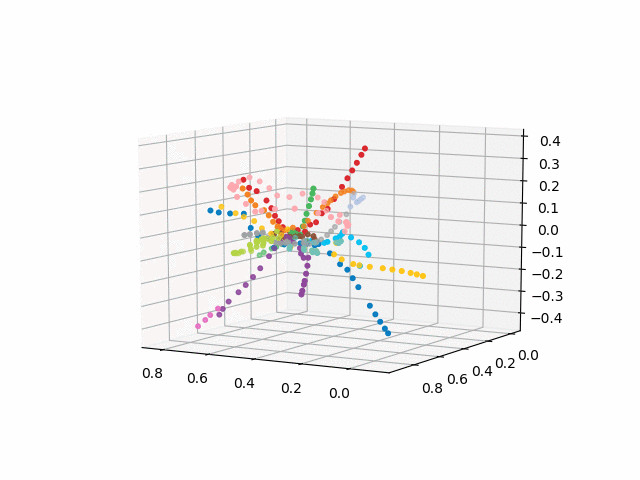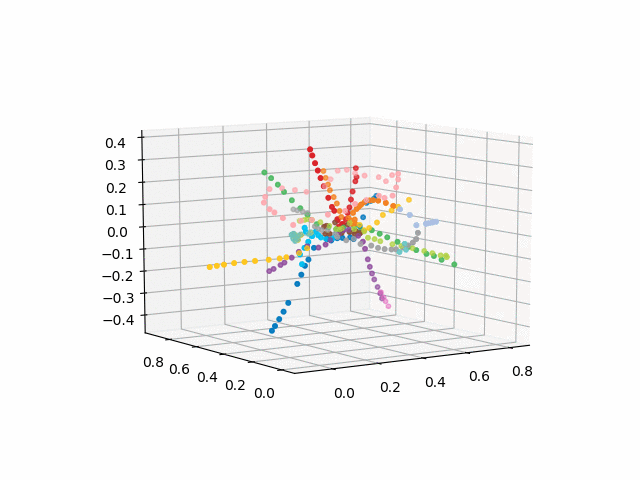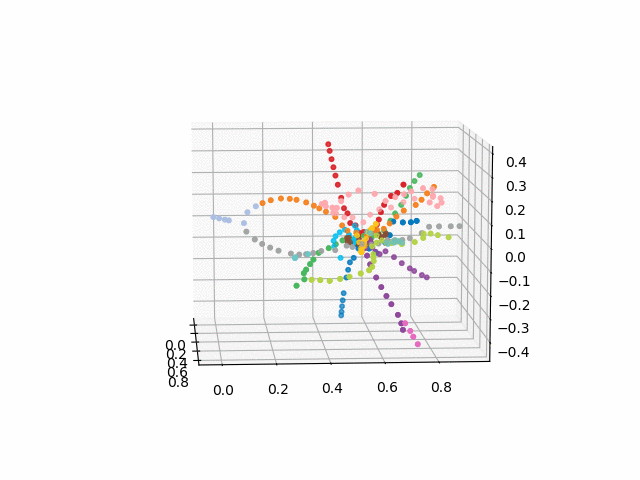
الإصدار بدون نص يبدو أكثر جمالا ويمكن التعرف عليه:
xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] colors=[ccode[lines[idi]] for idi in myIDs] xyzn = zip(xn, yn, zn) fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(xn,yn,zn, c=colors, marker='o') plt.show()
UPD: إضافة خطوط المترو من اللون المطلوب وإنشاء GIF. خطوط سوداء - التحولات بين المحطات:
myedges=[(myIDs.index(edge[0]),myIDs.index(edge[1]))for edge in G.edges] xn = fincoords[0][:,0] yn = fincoords[0][:,1] zn = fincoords[0][:,2] l=[labels[idi] for idi in myIDs] c=[ccode[lines[idi]] for idi in myIDs] fig = plt.figure() ax = fig.gca(projection='3d') ax.scatter(x,y,z, c=c, marker='o',s=25) for edge in myedges: col='black' if c[edge[0]]==c[edge[1]]: col=c[edge[0]] ax.plot3D([x[edge[0]], x[edge[1]]], [y[edge[0]], y[edge[1]]], [z[edge[0]], z[edge[1]]], col) ims = [] def rotate(angle): ax.view_init(azim=angle) rot_animation = animation.FuncAnimation(fig, rotate, frames=np.arange(0, 362, 3), interval=70) rot_animation.save('rotation2.gif', dpi=80, writer=matplotlib.animation.PillowWriter(80))
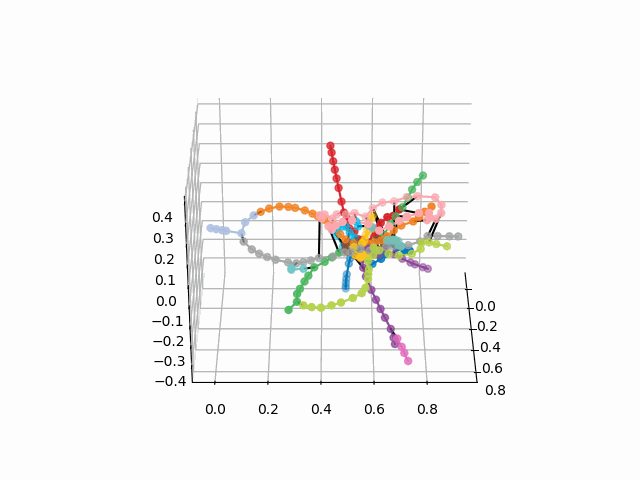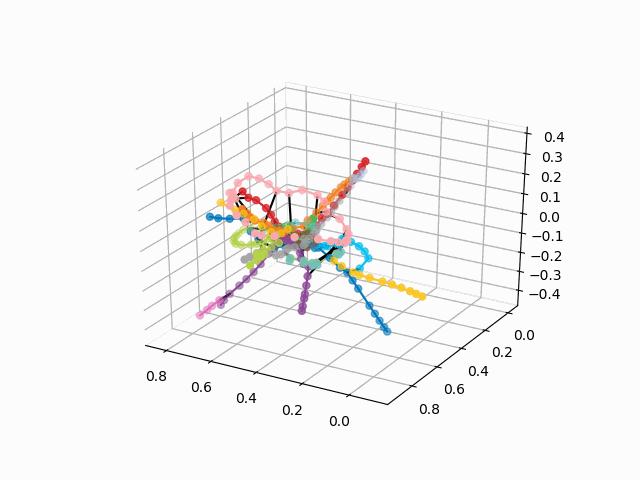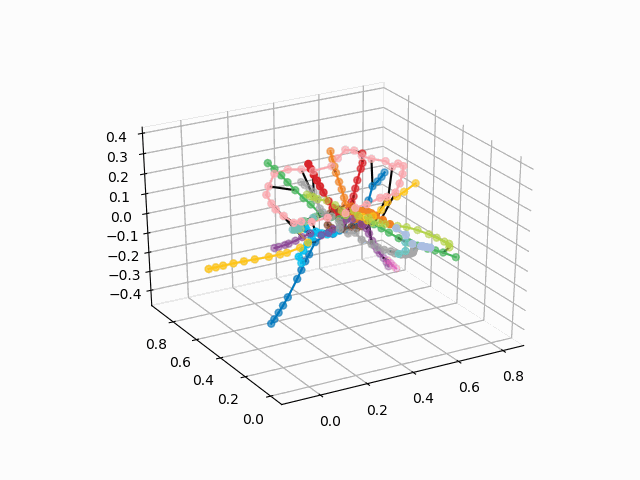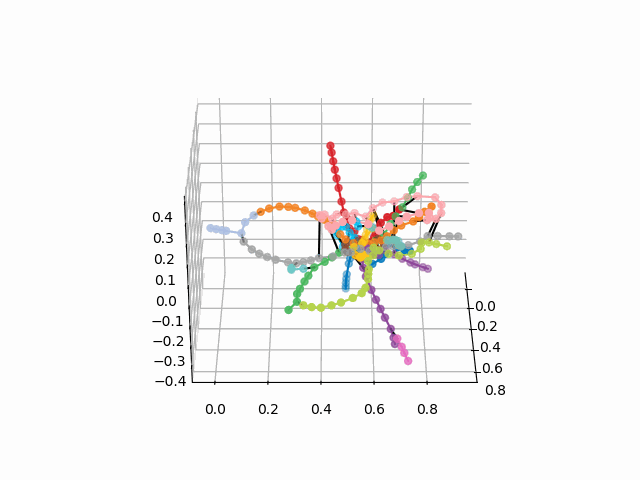
من هذا المخطط ، يمكن استخلاص بعض الاستنتاجات المثيرة للاهتمام التي ليست واضحة من المخططات الأخرى. بالنسبة إلى بعض الفروع ، على سبيل المثال ، الأخضر أو الأزرق أو الأرجواني ، فإن MCC (الحلقة الوردية) تكون عديمة الفائدة تقريبًا بسبب عمليات الزرع غير المريحة ، والتي تظهر في مسافة الحلقة من هذه الفروع. أطول الطرق - من شقة مشتركة إلى طريق سريع أو يوم الجمعة (خيول حمراء وزهرية / زرقاء) ، والطرق الطويلة هي أيضًا رواية قصة ألما-آتا وبونين ألي-نيكراسوفكا. بناءً على الخطة ، يوجد في شمال موسكو ازدواج جزئي للفروع الرمادية والخضراء الفاتحة - فهي قريبة من المخطط. سيكون من المثير للاهتمام أن نرى كيف الخطوط الجديدة (WDC ، BKL) والذين سوف تستخدمها في كثير من الأحيان. على أي حال ، آمل أن تكون مثل هذه المخططات أدوات مهمة للتحليل والإلهام وتخطيط السفر.
PS 3D ليس ضروريًا ، بالنسبة للإصدار الثنائي الأبعاد يكفي لتصحيح الكود قليلاً. ولكن في حالة المخطط ثنائي الأبعاد ، من المستحيل تحقيق هذه الدقة للمسافات.