الطرق شبه النيوتونية ، أو عندما يكون هناك الكثير من المشتقات الثانية لأثوس

عند التعارف الأول مع الأساليب شبه النيوتونية قد يفاجأ المرء مرتين. أولاً ، بعد إلقاء نظرة سريعة على الصيغ ، تثور الشكوك حول إمكانية نجاح ذلك على الإطلاق. ومع ذلك ، فإنها تعمل. علاوة على ذلك يبدو من المشكوك فيه أنها ستعمل بشكل جيد. ومن المثير للدهشة أن نرى مدى سرعة تواجدها مقارنة بالتغيرات المختلفة للنسب المتدرجة ، ليس في المهام التي تم إنشاؤها خصيصًا ، بل في المهام الحقيقية المأخوذة من الممارسة. وإذا كانت هناك بعد ذلك شكوك مختلطة مع الاهتمام ، فأنت بحاجة إلى فهم سبب نجاح هذا الشيء على الإطلاق.

الأصل والأفكار الأساسية التي تدفع أساليب التدرج ، بما في ذلك طريقة نيوتن ، قد تم النظر فيها بالفعل . أي أننا اعتمدنا على المعلومات المتعلقة بسلوك الوظيفة في محيط الموضع الحالي ، مما يعطينا تحليلًا رياضيًا بسيطًا. كحد أدنى ، كان من المفترض أن المعلومات المتعلقة بالمشتقات الأولى كانت متاحة لنا. ماذا لو كان هذا هو كل ما هو متاح لنا؟ هو التدرج النسب الجملة لدينا؟ بالطبع ، نعم ، ما لم تتذكر فجأة أننا نتعامل مع عملية تتم فيها معالجة الوظيفة الهدف بشكل صحيح. وإذا كان الأمر كذلك ، فلماذا لا نستخدم المعلومات المتراكمة حول سلوك الوظيفة من أجل جعل مسيرتنا على سطحها أقل عمياء قليلاً؟

تكمن فكرة استخدام المعلومات حول المسار المغطى في معظم الطرق لتسريع طرق النزول. تتناول هذه المقالة واحدة من أكثر الطرق فعالية ، وإن لم تكن أرخص ، طريقة المحاسبة لهذا النوع من المعلومات ، مما يؤدي إلى فكرة الطرق شبه النيوتونية.

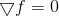
من أجل فهم من أين تنمو أرجل الطرق شبه النيوتونية ومن أين يأتي الاسم ، علينا مرة أخرى العودة إلى طريقة التصغير استنادًا إلى الحل المباشر لمعادلة النقاط الثابتة . تمامًا مثلما نظرنا في طريقة نيوتن المطبقة على حل هذه المعادلة إلى طريقة التحسين التي تحمل نفس الاسم (والتي ، على عكس سلفها ، لديها منطقة تقارب عالمية) ، يمكننا أن نتوقع أن يكون النظر في طرق أخرى لحل أنظمة المعادلات غير الخطية مثمرًا في خطط للأفكار لبناء طرق التحسين الأخرى.

طرق ثانية

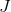
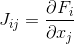
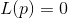
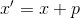
اسمحوا لي أن أذكركم بأن طريقة نيوتن لحل نظام المعادلات ، يعتمد على الاستبدال في الحي لبعض نقطة قريبة من الحل وظائف تقريبه الخطي حيث هو المشغل الخطي ، الذي ، متى هو ناقل و لديه مشتقات جزئية فيما يتعلق بكل متغير ، يتزامن مع مصفوفة جاكوبي . بعد ذلك ، يتم حل المعادلة و نقطة تؤخذ تقريب جديد إلى الحل المطلوب. انها بسيطة وتعمل.

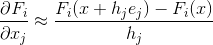
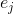
ولكن ماذا لو أننا لسبب ما لا نستطيع حساب مصفوفة جاكوبي؟ أول ما يتبادر إلى الذهن في هذه الحالة هو أنه إذا لم نتمكن من حساب المشتقات الجزئية من الناحية التحليلية ، فيمكننا إذن الحصول على تقريب رقمي لهم. يمكن أن يكون أبسط (على الرغم من عدم وجود الخيار الوحيد) لهذا التقريب صيغة الاختلافات الصحيحة الصحيحة: حيث هو ناقل قاعدة jth. المصفوفة المكونة من مثل هذه التقريبات ستتم الإشارة إليها بواسطة . 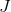تحليل لمقدار الاستبدال في في طريقة نيوتن ، يؤثر تقاربها على تكريس عدد كبير من الأعمال ، لكن في هذه الحالة نحن مهتمون بجانب آخر. وهي تتطلب مثل هذا التقريب حساب الوظيفة عند نقاط إضافية N ، بالإضافة إلى الوظيفة في هذه النقاط يحرف وظيفة ، أي



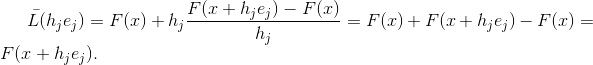
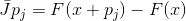
ليست كل خاصية تقريب لمصفوفة Jacobi تحتوي على هذه الخاصية ، ولكن كل مصفوفة دالة تقارب لها هذه الخاصية هي تقريب لمصفوفة Jacobi. في الواقع ، إذا و ثم في . هذه الخاصية ، وهي خاصية الاستيفاء ، تعطينا طريقة بناءة لتعميم طريقة نيوتن.

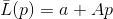
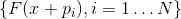
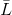
سمح - وظيفة تلبية الاحتياجات لبعض نظام ناقلات مستقلة خطيا . ثم تسمى هذه الوظيفة وظيفة ثانوية والمعادلة التي تحددها هي المعادلة الثانية . إذا كان نظام المتجهات اكتمال (أي ، هناك بالضبط N منهم وأنها لا تزال مستقلة خطيا) ، وبالإضافة إلى ذلك ، نظام ناقلات مستقلة خطيا بعد ذلك محددة بشكل فريد.

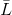
أي طريقة تعتمد على التغيير المحلي للمعادلة معادلة النموذج حيث يرضي المعادلة الثانية ، وتسمى الطريقة الثانية .

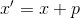
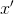
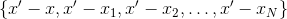
يطرح سؤال عادل حول كيفية بناء secant لوظيفة في الطريقة الأكثر عقلانية. . يبدو السطر التالي من الاستدلال واضحًا: فليتم بناء نموذج تقارب عند النقطة x التي تقحم الوظيفة المعطاة عند النقاط . حل المعادلات يعطينا نقطة جديدة . ثم لبناء نموذج أفيني في مرحلة ما من الأكثر منطقية اختيار نقاط الاستيفاء بحيث تكون القيمة معروف بالفعل - وهذا هو ، أخذه من المجموعة . هناك خيارات مختلفة يمكن من خلالها اختيار النقاط من بين العديد من الأشياء المستخدمة سابقًا. 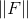على سبيل المثال ، يمكنك أن تأخذ نقاط الاستيفاء تلك التي فيها يهم الأقل أو الأول فقط نقطة. في أي حال ، يبدو واضحا ذلك ينبغي أن تدرج في العديد من نقاط الاستيفاء لنموذج أفيني الجديد. 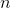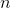بعد ذلك خطوات العملية التكرارية في مجموعتنا يمكن أن تصل إلى النزوح مبنية على نقاط مرت سابقا. إذا كانت العملية مبنية بطريقة لا يستخدم فيها النموذج الجديد من القيم السابقة ، ثم تسمى هذه العملية طريقة p-point secant.

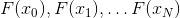
للوهلة الأولى ، قد يبدو أن طريقة N-point secant هي أفضل مرشح لدور استبدال طريقة Newton ، حيث إنها تستفيد إلى أقصى حد من المعلومات التي نحصل عليها في عملية الحل ، مع تقليل عدد العمليات الحسابية إلى الحد الأدنى - نحن نستخدم قيمة الوظيفة في الأخير مرت نقاط N. لسوء الحظ ، هذا ليس كذلك. الشيء هو أن نظام ناقل يرفض بعناد أن يكون مستقلا خطيا مع N. كبيرة بما فيه الكفاية. بالإضافة إلى ذلك ، حتى لو تبين أن هذا الشرط قد تم الوفاء به وما زال نموذج affine المقابلة ، ثم هناك فرصة أن الاتجاهات يثبت أيضا أن تكون مستقلة خطيا ، اتضح حتى أقل. وهذا يستلزم حقيقة أن نموذج أفيني ، على الرغم من وجوده ، يتدهور وغير مناسب عمليا.

بشكل عام ، الأكثر استقرارًا هو الطريقة الثانية المكونة من نقطتين. وهذا هو ، الطريقة التي في كل التكرار لدينا لحساب قيم N-1 إضافية للدالة. من الواضح أن هذا غير مناسب لأغراضنا العملية.

ثم السؤال هو - ماذا كان كل هذا؟

الطرق شبه النيوتونية لحل المعادلات

المخرج بسيط ، رغم أنه غير واضح. إذا لم يكن لدينا القدرة التقنية ، استنادًا إلى القيم المحسوبة بالفعل ، على تحديد نموذج affine الذي يلبي المعادلة secant بشكل فريد ، فهذا غير ضروري. نأخذ معادلة الثواني كأساس ، لكننا سنشترط أن تكون راضيًا فقط عن نظام ناقلات غير مكتمل . بمعنى آخر ، سوف نطلب أن يكون شرط الاستيفاء مستوفياً فقط لعدد صغير بما فيه الكفاية من القيم المعروفة. بالطبع ، في هذه الحالة لم يعد بإمكاننا ضمان أن المصفوفة المستخدمة في مثل هذا النموذج تميل إلى مصفوفة جاكوبي ، لكننا لن نحتاج إلى ذلك. إضافة إلى ذلك ، يجب على نموذج affine استيفاء الوظيفة عند النقطة الحالية ، أي ، نحصل على الصيغة التالية للطريقة الثانية:



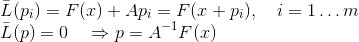
كان Bruiden أول من فكر في طرق من هذا النوع بالنسبة إلى m = 1 ، ووصفها بأنها شبه نيوتونية. من الواضح أن الحالة الثانية في هذه الحالة تسمح لنا بتحديد المصفوفة بشكل فريد فقط في حالة فرض شروط إضافية عليها ، وكل شرط إضافي يؤدي إلى طريقة منفصلة. برويد نفسه مسبب كما يلي:

كما الحركة في الاتجاه من نقطة الى هذه النقطة لا يقدم لنا أي معلومات إضافية حول كيفية تغير الوظيفة في غير الاتجاهات ، ثم تأثير وظيفة أفيني جديدة على المتجه يجب أن يختلف تأثير الوظيفة القديمة على نفس المتجه كلما كان الاختلاف أقل من . كملاذ أخير ، متى متعامد ، يجب ألا يختلف سلوك الوظيفة الجديدة عن سلوك القديم.

فكرة برايدن رائعة في بساطتها. في الواقع ، إذا لم يكن لدينا معلومات جديدة حول سلوك الوظيفة ، فإن أفضل ما يمكننا فعله هو محاولة عدم إبطال الوظيفة القديمة. ثم الشرط الإضافي

للجميع مثل هذا

يتيح لك تحديد مصفوفة التحول الجديد بشكل فريد - يتم الحصول عليها عن طريق إضافة تصحيح من المرتبة 1 إلى المصفوفة القديمة.



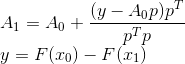
ومع ذلك ، على الرغم من بساطة وتوافق الاستنتاجات التي توصل إليها Bruiden ، فإنها لا توفر نقطة ارتكاز يمكن أن تكون بمثابة أساس لبناء أساليب أخرى مماثلة. لحسن الحظ ، هناك تعبير أكثر رسمية عن فكرته. وهي مصفوفة شيدت بهذه الطريقة اتضح أنه الحل للمشكلة التالية:



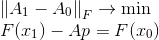
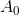
إن قيد المهمة ليس سوى المعادلة الثانية ، وحالة التقليل تعكس رغبتنا في حفظ أكبر قدر ممكن من المعلومات في المصفوفة . مقياس التباين بين المصفوفات في هذه الحالة هو القاعدة Frobenius ، حيث المشكلة التي تنطوي على حل لا لبس فيه. قد تكون هذه الصيغة بمثابة نقطة انطلاق لبناء طرق أخرى. أي ، يمكننا تغيير كل من المقياس الذي نقيم به التغييرات التي تم إدخالها ونشدد الشروط المفروضة على المصفوفة. بشكل عام ، يمكن للمرء أن يعمل بالفعل مع مثل هذه الصيغة للطريقة.

شبه الأمثل نيوتن أساليب

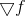
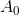
بعد فهم الفكرة الرئيسية ، يمكننا أخيرًا العودة إلى مشاكل التحسين ونلاحظ أن تطبيق صيغة Bruyden لإعادة حساب نموذج القائد لا يناسب مهمتنا جيدًا. في الواقع ، أول مشتق من وظيفة التدرج لا يوجد شيء آخر غير مصفوفة هسيان ، التي هي متماثلة من خلال البناء. في الوقت نفسه ، يؤدي التحديث وفقًا لقاعدة Bruyden إلى مصفوفة غير متماثلة حتى لو كان متماثل. هذا لا يعني أنه لا يمكن تطبيق طريقة Bruden لحل معادلة النقاط الثابتة ، ولكن استنادًا إلى قاعدة التحديث هذه ، من غير المحتمل أن نكون قادرين على إنشاء طرق تحسين جيدة. بشكل عام ، من الواضح تمامًا أن الطريقة شبه نيوتن يجب أن تعمل بشكل أفضل ، وكلما كان نظام ظروف المشكلة يصف بدقة تفاصيل مصفوفة جاكوبي المحددة.

لتصحيح هذا العيب ، نضيف قيدًا إضافيًا إلى مشكلة تقليل Bruden ، مما يتطلب صراحةً أن تكون المصفوفة الجديدة متماثلة مع الأخرى القديمة:



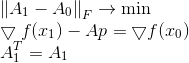
الحل لهذه المشكلة هو



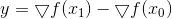
هنا ، وتمت تسمية صيغة إعادة حساب المصفوفة باسم منشئيها - Powell و Shanno و Bruyden (PSB). المصفوفة الناتجة متناظرة ، ولكن من الواضح أنها ليست إيجابية محددة ، ولو فجأة لن يكون الخطية . ورأينا أن اليقين الإيجابي أمر مرغوب فيه للغاية في أساليب التحسين.

مرة أخرى ، سوف نقوم بتصحيح حالة المشكلة ، وذلك باستخدام قاعدة Frobenius المقاسة هذه المرة كمقياس للإنحراف المصفوفي.



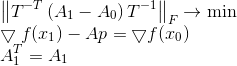
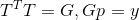
أصل مثل هذا البيان للسؤال هو موضوع كبير منفصل ، ولكن من المثير للاهتمام أنه إذا كانت المصفوفة T هي هكذا (أي ، G هي أيضًا مصفوفة تحويل تقارب ترضي المعادلة الثانية للاتجاه p) ، ثم يتضح أن حل هذه المشكلة مستقل عن اختيار T ويؤدي إلى صيغة التحديث



المعروفة باسم صيغة ديفيدون فليتشر باول. أثبتت طريقة التحديث هذه في الممارسة العملية ، لأنها تحتوي على الخاصية التالية:

إذا و 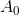واضح إيجابي بعد ذلك أيضا تحديد إيجابي.

وألاحظ بعد ذلك أنه إذا لم يتم استيفاء الشرط الأول ، فلا توجد وظيفة تقارب بمصفوفة محددة ترضي المعادلة الثانية.

إذا كنا في المشكلة التي تؤدي إلى طريقة DFP ، فإننا نأخذ ، كمقياس لتناقض نماذج أفين ، المسافة بين المصفوفات نفسها ، ولكن بين المصفوفات التي تعكسها ، نحصل على مشكلة في النموذج



حلها هو صيغة معروفة ، واكتشفت في وقت واحد تقريبًا من قبل بريدين وفليتشر وجولدفارب وشانو (BFGS).



حتى الآن ، يُعتقد أن إعادة الحساب وفقًا لهذه الصيغة هي الأكثر كفاءة من الناحية الحسابية وفي الوقت نفسه تكون أقل عرضة لتنكس المصفوفة بعدد كبير من التكرارات. تحت نفس شروط DFP ، تحافظ هذه الصيغة على خاصية التحديد الإيجابي.

تتطلب جميع الطرق الموضحة لتحديث المصفوفة تصحيحًا للصف 2. وهذا يجعل من السهل والعكس عكس المصفوفة باستخدام صيغة شيرمان موريسون والقيمة .



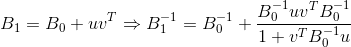
شريطة أن يكون قاسم الصيغة غير صفرية. لن أقدم صيغ محددة لتحديث المصفوفات العكسية للطرق المدرجة ، حيث يسهل العثور عليها أو اشتقاقها بشكل مستقل. الشيء الوحيد الذي يجب ملاحظته في هذه الحالة هو أن أنواع الطرق مع تحديث المصفوفة العكسية عادة ما تكون أقل استقرارًا (أي أنها تعاني أكثر من أخطاء التقريب) من تلك التي تقترح تحديث المصفوفة الأصلية. من الأكثر فعالية تحديث المصفوفة نفسها ، ولكن تحلل Cholesky الخاص بها (ما لم يحدث هذا التحلل بالطبع) ، لأن خيار التنفيذ هذا يكون أكثر استقرارًا من الناحية العددية ، بالإضافة إلى أنه يقلل من تكلفة حل المعادلة التي تحدد اتجاه الحركة.

يبقى أن ننظر في مسألة كيف يجب أن تبدو المصفوفة الأولى في العملية شبه النيوتونية. كل شيء واضح هنا - كلما اقتربنا من مصفوفة هيسان أو نسخته المصححة ، إذا لم يتحول هسي فجأة إلى كونه إيجابيًا ، فكلما كان ذلك أفضل من وجهة نظر التقارب. ومع ذلك ، من حيث المبدأ ، يمكن أن تكون أي مصفوفة محددة إيجابية مناسبة لنا. أبسط إصدار لمثل هذه المصفوفة هو نسخة واحدة ، ثم يتزامن التكرار الأول مع تكرار نزول التدرج. أظهر Fletcher و Powell (بشكل طبيعي ، بالنسبة لطريقة DFP) أنه إذا تم تقليل الوظيفة التربيعية ، بغض النظر عن المصفوفة (الإيجابية المحددة) المستخدمة كتكرار DFP الأولي ، فسيؤدي ذلك إلى حل في تكرار N بالضبط ، حيث N بعد المشكلة ، وتتزامن المصفوفة شبه النيوتونية مع المصفوفة هسه في الحد الأدنى. في الحالة العامة غير الخطية لمثل هذه السعادة ، نحن ، بالطبع ، لن ننتظر ، ولكن هذا على الأقل يعطي سبباً لعدم القلق كثيرًا بشأن الاختيار السيئ للمصفوفة الأولية.

استنتاج

النهج الموصوف لبناء الطرق شبه النيوتونية ليس هو النهج الوحيد الممكن. على الأقل ، توصل مكتشفو الطرق شبه النيوتونية الموصوفة والعديد من الباحثين اللاحقين إلى نفس الصيغ على أساس اعتبارات مختلفة تمامًا. ومع ذلك ، من المثير للاهتمام أنه بمجرد ظهور طريقة شبه نيوتونية معينة ، ثم بغض النظر عن طريقة الحصول عليها ، بعد وقت قصير إلى حد ما أصبح من الواضح أنه كان حلاً لمشكلة تحسين سهلة التفسير. في رأيي ، من اللافت للنظر أنه من الممكن إحضار بعض القاسم المشترك لهذه الأساليب المتنوعة ، لأن هذا يوفر الأساس لبناء طرق أخرى تأخذ بعين الاعتبار بشكل خاص تفاصيل مهمة معينة. على وجه الخصوص ، هناك طرق شبه نيوتونية مصممة لتحديث المصفوفات المتفرقة ، وهي طرق يتعرض فيها أقل عدد ممكن من العناصر للتغيير ، وسيكون الكثير من الآخرين خيالًا.

تجدر الإشارة أيضًا إلى أن أساليب المقاييس المتغيرة ، على الرغم من اسمها ، لا تؤدي دائمًا إلى بناء مصفوفات ، والتي هي بالفعل مقاييس ، على الرغم من أنها تفعل ذلك في كل مرة يكون ذلك ممكنًا على الإطلاق.هذه ليست مشكلة كبيرة عادة ، لكن أولئك الذين يريدون حماية أنفسهم من أي حرج محتمل قد يلجئون إلى نفس الحيل التي تم إجراؤها للتغلب على مشكلة مماثلة في طريقة نيوتن - على سبيل المثال ، عن طريق تغيير الاتجاه أو تطبيق مخطط ليفنبرغ - ماركوارت . صحيح ، في هذه الحالة ، ستصبح الأسئلة المتعلقة باختيار شكل منطقة موثوقة ذات صلة مرة أخرى ، ولكن عليك هنا اختيار أقل الشرور. الحل الآخر لهذه المشكلة هو استخدام طرق البحث الخطي لضمان استيفاء الشروط اللازمة للحفاظ على اليقين الإيجابي. يضمن حكم Wolfe تحقيق هذا الشرط ، في حين أن قواعد Armijo و Goldstein لا.

, . , ( , , N , , ). ( , , ), . , , — . — .