داخل ذا جيموك. هياكل البيانات الأساسية: إقران كومة الذاكرة المؤقتة وشجرة الصور النقطية

غالبًا ما ينبثق موضوع Allocators على الإنترنت: في الواقع ، يعتبر Allocator نوعًا من حجر الأساس ، أي قلب أي تطبيق. في هذه السلسلة من المنشورات ، أود أن أتحدث بالتفصيل عن أحد التخصيصات البارزة والممتازة - JeMalloc ، المدعومة والمطورة بواسطة Facebook واستخدامها ، على سبيل المثال ، في bionic [Android] lib C.

على الشبكة ، لم أجد أي تفاصيل تكشف بالكامل عن روح هذا التخصيص ، مما أثر في النهاية على استحالة إجراء أي استنتاجات حول قابلية تطبيق JeMalloc في حل مشكلة معينة. تم طرح الكثير من المواد ، ومن أجل قراءتها لم تكن متعبة ، أقترح البدء بالأساسيات: هياكل البيانات الأساسية المستخدمة في JeMalloc.

تحت القطة ، أنا أتحدث عن إقران كومة الذاكرة المؤقتة وشجرة الصور النقطية ، والتي تشكل أساس JeMalloc. في هذه المرحلة ، لا أتطرق إلى موضوع تعدد مؤشرات الترابط وغلق الحبيبات الدقيقة ، لكن مع استمرار سلسلة المنشورات ، سوف أخبرك بالتأكيد بهذه الأمور ، من أجل ، في الواقع ، يتم إنشاء أنواع مختلفة من الأنواع الغريبة ، خاصة تلك الموضحة أدناه.

Bitmap_s هي بنية بيانات شبيهة بالشجرة تتيح لك:

• العثور بسرعة على أول مجموعة / بت تعيين في تسلسل بت معين.
• تغيير والحصول على قيمة قليلا مع الفهرس i في تسلسل معين من البتات.
• تم بناء الشجرة وفقًا لسلسلة من n bits ولديها الخصائص التالية:
• الوحدة الأساسية للشجرة هي العقدة ، والوحدة الأساسية للعقدة هي بت. تتكون كل عقدة من وحدات k تمامًا. يتم تحديد شاهد العقدة بحيث يتم حساب العمليات المنطقية على مجموعة محددة من البتات بأسرع وقت ممكن وبكفاءة ممكنة على جهاز كمبيوتر معين. في JeMalloc ، يتم تمثيل العقدة بنوع طويل غير موقّع .
• يتم قياس ارتفاع الشجرة بمستويات ولسلسلة من البتات n هي H = $$$\ log_ {k} {n} log k (n)$المستويات.
• ويمثل كل مستوى من الشجرة بواسطة تسلسل $$$countOfNodesOnLevel = integerCeil (\ frac {n} {{k} ^ {H - currentLevel + 1}})$العقد ، وهو ما يعادل سلسلة من $$$countOfBitsOnLevel = countOfNodesOnLevel * k$الشيء.
• يتكون المستوى الأعلى (الجذر) من الشجرة من k bits ، والأدنى من n bits.
• تحدد كل جزء من عقدة المستوى L حالة جميع وحدات بت التابعة لعقدة فرعية من المستوى L - 1: إذا تم ضبط جزء ما على "مشغول" ، عندها يتم تعيين كل وحدات بت من العقدة الفرعية على "مشغول" ، وإلا ، ربما تحتوي أجزاء من عقدة تابعة على "مشغول" والدولة "الحرة".

من المعقول تمثيل bitmap_t في صفيفين: الأول ، لبعد يساوي عدد كل العقد الشجرية - لتخزين عقد الشجرة ، والثاني ، بعد ارتفاع الشجرة - لتخزين إزاحة بداية كل مستوى في صفيف عقدة الشجرة. باستخدام طريقة تحديد شجرة ، يمكن أن يذهب عنصر الجذر أولاً ، ثم بالتتابع ، العقد لكل مستوى من المستويات. ومع ذلك ، يخزن مؤلفو JeMalloc عنصر الجذر في الصفيف ، وأمامه توجد مستويات مستويات الشجرة الأساسية.

كمثال توضيحي ، خذ سلسلة من 92 بت وعقل K = 32. نحن نفترض أن الحالة "مجانية" - تدل عليها بت واحد ، والحالة "مشغول" - صفر. لنفترض أيضًا أنه في تسلسل البت الأصلي ، يتم ضبط البت مع الفهرس 1 (العد من الصفر ، من اليمين إلى اليسار في الشكل) على الحالة المزدحمة. عندئذٍ ستبدو الصورة النقطية لتسلسل البت مثل الصورة أدناه:



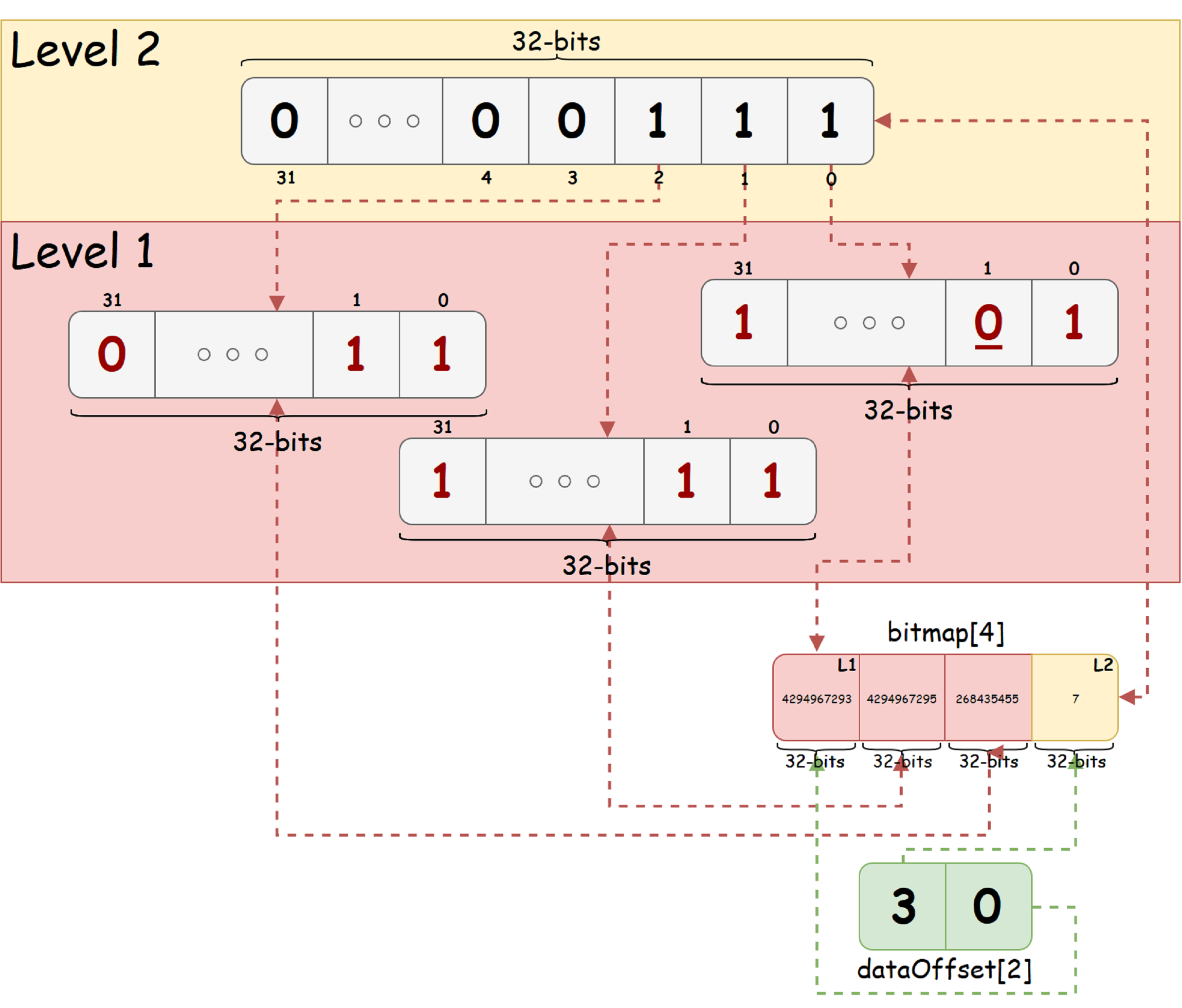من الشكل نرى أن الشجرة الناتجة لها مستويين فقط. يحتوي مستوى الجذر على 3 وحدات بت ، مما يشير إلى وجود كل من البتات الحرة والمحتلة في كل من العقد الفرعية للبت المقابل. في الركن الأيمن السفلي ، يمكنك مشاهدة طريقة العرض "شجرة" في صفيفين: جميع العقد شجرة والإزاحة من كل مستوى في صفيف العقدة.

على افتراض أن bitmap_t يمثله صفيفان (صفيف بيانات ومجموعة من إزاحات مستوى الشجرة في صفيف البيانات) ، فإننا نصف عملية البحث عن أول بت هام على الأقل في bitmap_t:

• بدءًا من العقدة الجذرية ، نقوم بإجراء عملية البحث عن أول جزء من العقدة الأقل أهمية: لحل هذه المشكلة ، تقدم المعالجات الحديثة إرشادات خاصة يمكنها تقليل وقت البحث بشكل كبير. سنقوم بحفظ النتيجة التي تم العثور عليها في المتغير FirstSetedBit .
• في كل تكرار للخوارزمية ، سنحتفظ بمجموع مواضع البتات التي تم العثور عليها: countOfSettedBits + = FirstSetedBit
• باستخدام نتيجة الخطوة السابقة ، نذهب إلى العقدة الفرعية لأول وحدة بت ذات أهمية على الأقل من العقدة ونكرر الخطوة السابقة. يتم الانتقال وفقًا للصيغة البسيطة التالية: $$$CurrentNode = bitmapData [levelOffsetArray [currentLevel] + sumOfBits]$
• تستمر العملية حتى يتم الوصول إلى أدنى مستوى من الشجرة. countOfSettedBits - عدد البت المطلوب في تسلسل بت الإدخال.

اقتران كومة هو بنية بيانات شجرة تشبه كومة الذاكرة المؤقتة التي تسمح لك:

• إدراج عنصر مع تعقيد وقت ثابت من O (1) والتكلفة المطفأة من O (سجل N) أو O (1) ، وهذا يتوقف على التنفيذ.
• ابحث على الأقل عن وقت ثابت - O (1)
• دمج كومة الاقتران مع تعقيد زمني ثابت - O (1) والتكلفة المطفأة O (log N) أو O (1) - اعتمادًا على التنفيذ
• حذف عنصر تعسفي (على وجه الخصوص ، عنصر واحد على الأقل) مع تقدير التعقيد المؤقت في O (N) وتقدير التعقيد المطفأ في O (log N)

وبشكل أكثر رسمية ، فإن Pairing Heap عبارة عن شجرة تعسفية لها جذر مخصص يرضي خصائص الكومة (مفتاح كل قمة ليس أقل / ليس أكثر من مفتاح أصلها).
تبدو كومة الاقتران النموذجية التي تكون فيها قيمة العقدة الفرعية أقل من قيمة العقدة الأصلية (وتعرف أيضًا باسم Min Pairing Heap) ، كما يلي:



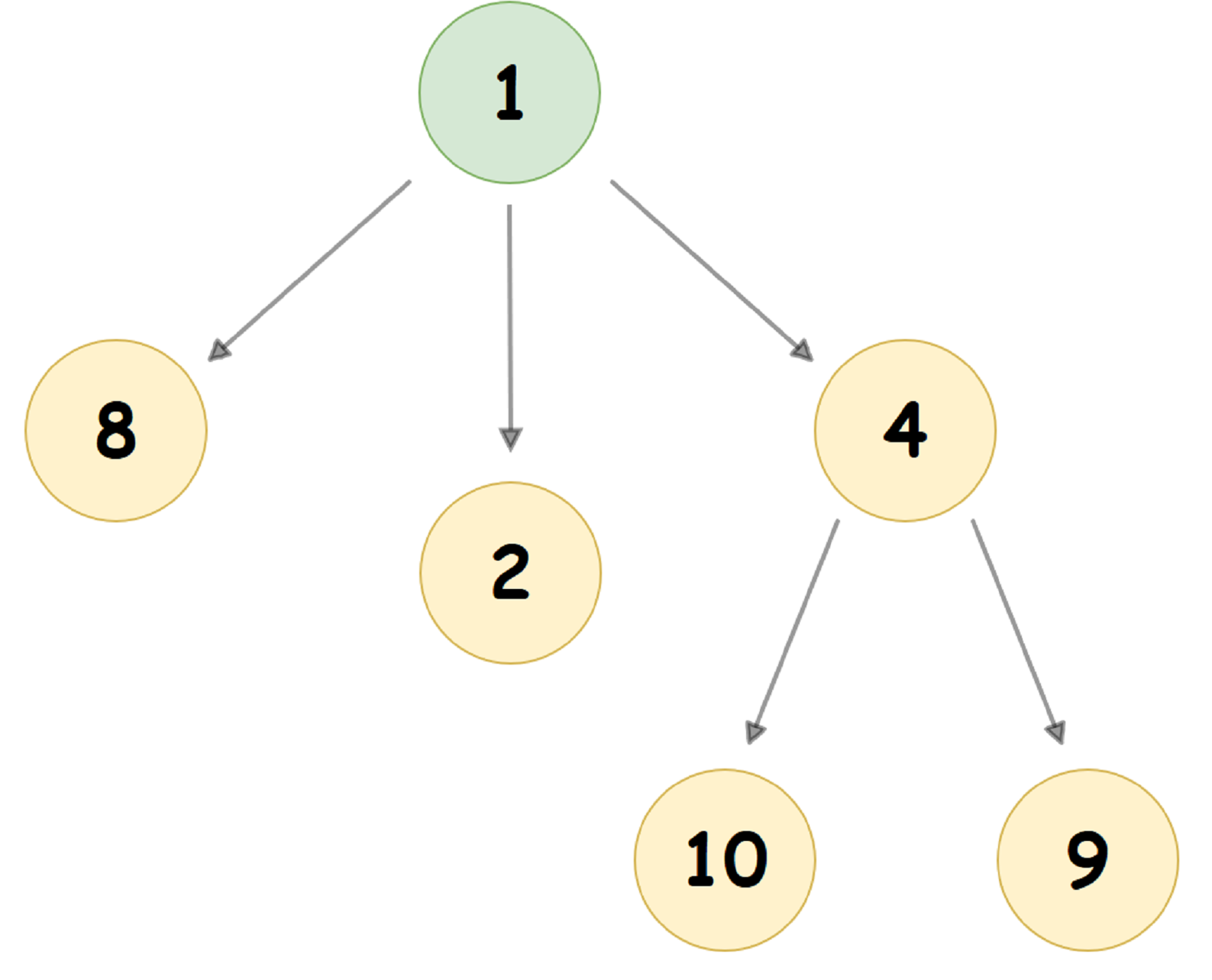
في ذاكرة الكمبيوتر ، يتم تقديم Pairing-Heap ، كقاعدة عامة ، بطريقة مختلفة تمامًا: تخزن كل عقدة من شجرة 3 مؤشرات:

• المؤشر إلى العقدة التابعة في أقصى اليسار للعقدة الحالية
• المؤشر إلى الأخوة اليسرى من العقدة
• المؤشر إلى الأخوة الصحيحة للعقدة

في حالة فقد أي من العقد المشار إليها ، يتم إلغاء مؤشر العقدة المقابل.
للحصول على الكومة المعروضة في الشكل أعلاه ، نحصل على التمثيل التالي:



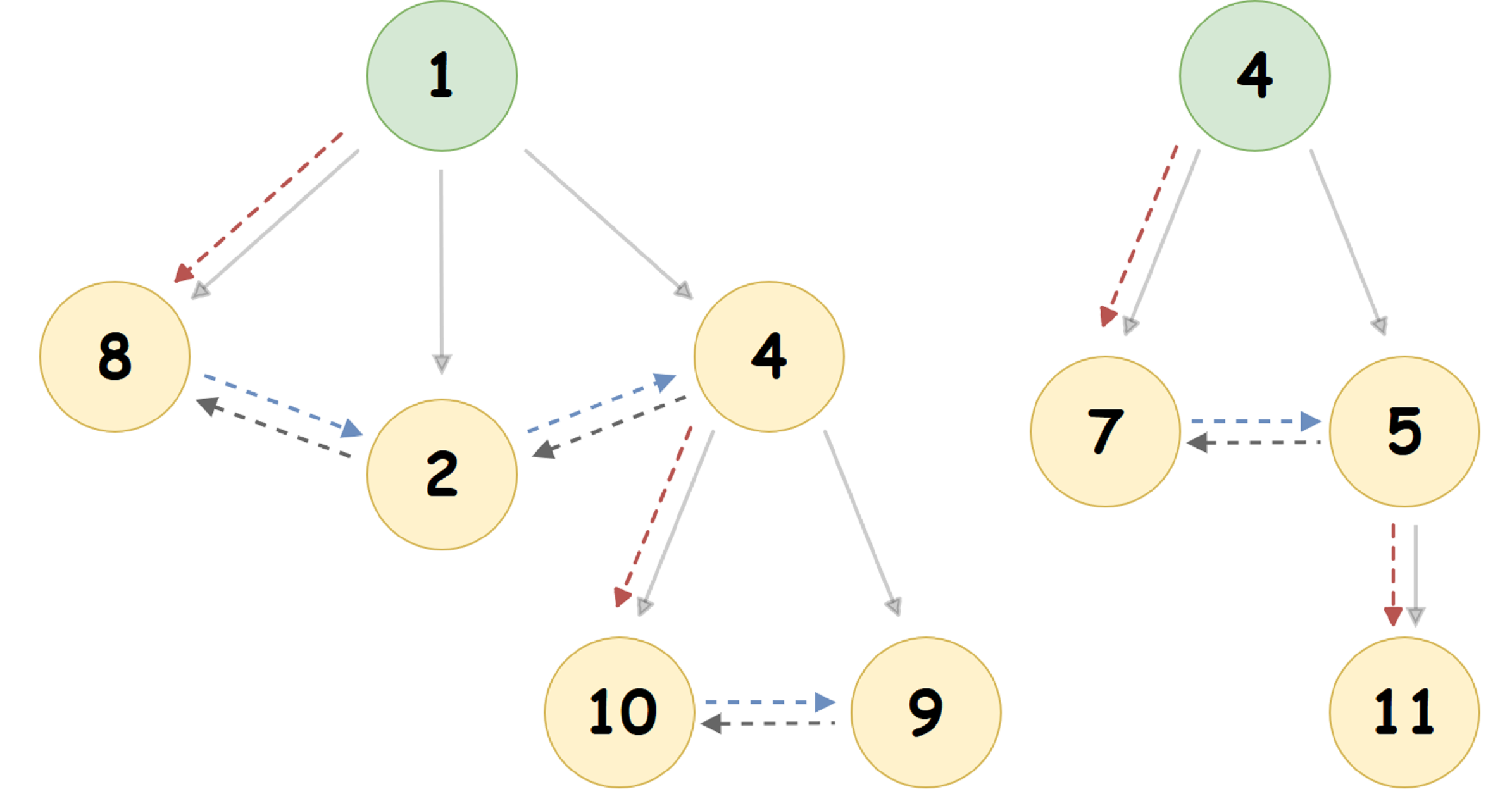هنا ، يتم الإشارة إلى المؤشر إلى أقصى عقدة تابعة لليسار بواسطة سهم أحمر منقط ، والمؤشر إلى الأخ الأيمن للعقدة باللون الأزرق ، والمؤشر إلى الأخ الأيسر رمادي. يعرض السهم الصلب تمثيل الاقتران كومة في شكل يشبه شجرة شائع للشخص.

يرجى ملاحظة الحقائق التالية:

• في جذر الكومة لا يوجد دائمًا أي إخوة يمين ويسار.
• إذا كان لدى أي عقدة U مؤشر غير صفري إلى العقدة الفرعية ذات أقصى اليسار ، فستكون هذه العقدة هي "رأس" القائمة المرتبطة بشكل مضاعف لجميع العقد الفرعية التابعة لـ U. وتسمى هذه القائمة siblingList.

بعد ذلك ، ندرج خوارزمية العمليات الرئيسية في Min Pairing-Heap :

• إدراج العقدة في الاقتران كومة:
  
  دع هناك تعطى كومة إقران مع جذر وقيمة فيها {R ، V_1} ، وكذلك عقدة {U ، V_2} . ثم ، عند إدراج عقدة U في كومة الاقتران المحددة:
  
  • إذا تم استيفاء الشرط V_2 <V_1: تصبح U العقدة الجذرية الجديدة للكومة ، "مزاحمة" الجذر R إلى موضع العقدة التابعة اليسرى. في الوقت نفسه ، يصبح الأخ الأيمن للعقدة R أقدم عقدة في أقصى اليسار ، ويصبح المؤشر إلى العقدة اليسرى إلى العقدة R صفراً.
  • بخلاف ذلك: تصبح U العقدة الأبعد من جذر R ، ويكون أخيها الأكبر العقدة اليسرى من جذر R.
• دمج اثنين من كومة الاقتران:
  
  اسمح لإثنين من أكوام الاقتران بجذور وقيم فيها {R_1، V_1} ، {R_2، V_2} على التوالي. نحن نصف إحدى الخوارزميات لدمج هذه الأكوام في كومة الاقتران الناتجة:
  
  • اختر الكومة مع أدنى قيمة في الجذر. فليكن حفنة من {R_1 ، V_1}.
  • "فصل" الجذر R_1 عن الكومة المحددة: لهذا ، نقوم ببساطة بإلغاء مؤشرها إلى العقدة الفرعية ذات أقصى اليسار.
  • باستخدام المؤشر الجديد إلى العقدة الفرعية الموجودة في أقصى اليسار من الجذر R_1 ، قم بإجراء الجذر R_2. لاحظ أنه من الآن فصاعدًا ، يفقد R_2 حالة الجذر ويمثل عقدة عادية في الكومة الناتجة.
  • سنقوم بتعيين الأخ المناسب للعقدة R_2: مع القيمة الجديدة ، سنقوم بتحويل المؤشر القديم (قبل التصفير) إلى العقدة الفرعية الموجودة في أقصى اليسار من الجذر R_1 ، وبالنسبة إلى R_1 ، على التوالي ، قم بتحديث المؤشر إلى الأخ الأيسر.

النظر في خوارزمية دمج باستخدام مثال محدد:



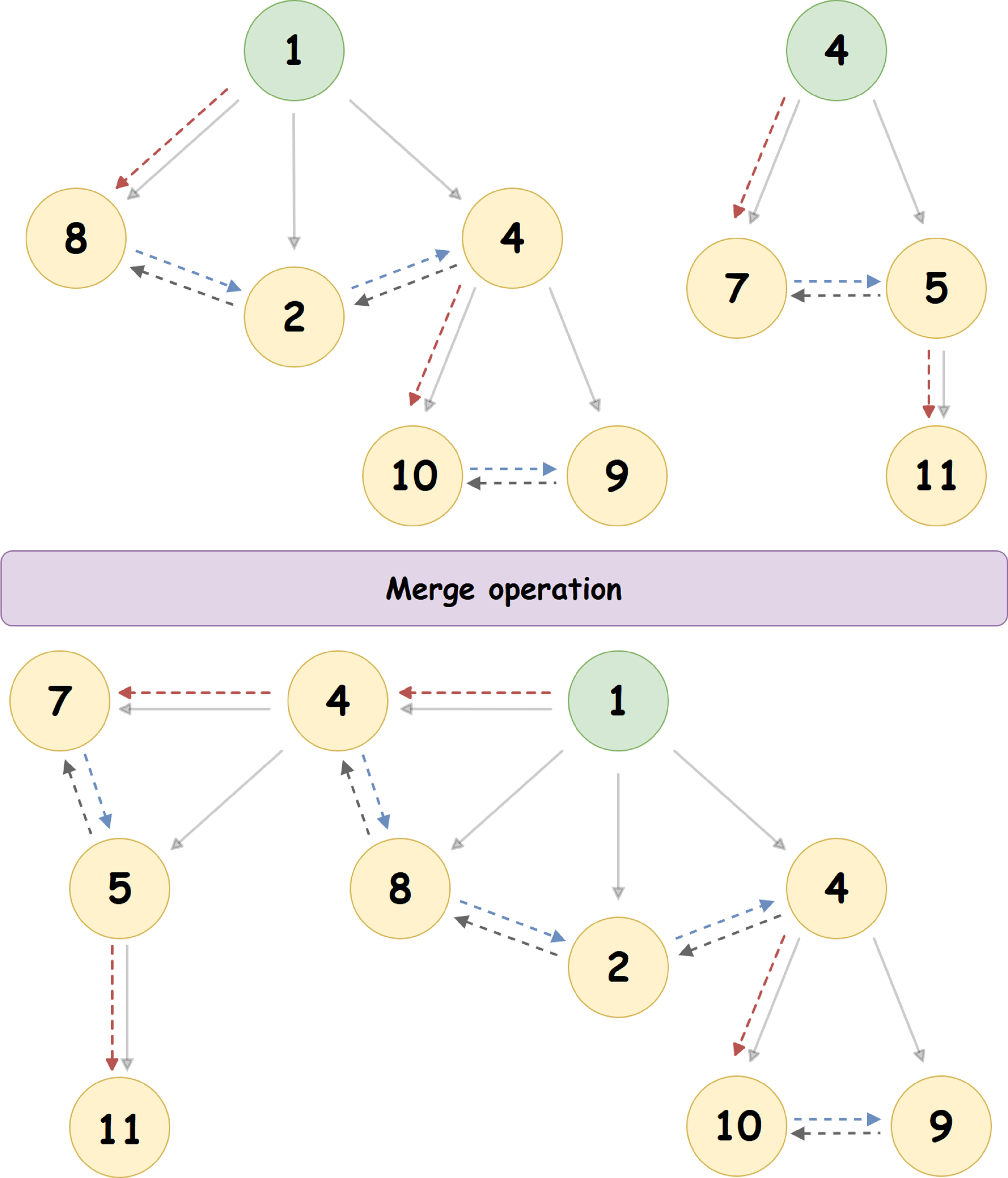هنا ، تربط الكومة ذات الجذر '4' الكومة مع الجذر '1' (1 <4) ، لتصبح العقدة الفرعية التابعة لها. يتم تحديث المؤشر إلى الأخ الأيمن للعقدة '4' ، وكذلك المؤشر إلى الأخ الأيسر للعقدة '8'.

• إزالة الجذر (العقدة مع الحد الأدنى للقيمة)
  
  هناك عدة خوارزميات لإزالة عقدة من كومة الاقتران ، مضمونة لإعطاء تقدير مطفئ من التعقيد في O (log N). نحن نصف واحدة منها ، تسمى خوارزمية multass وتستخدم في JeMalloc:
  
  
  • نقوم بحذف جذر الكومة المعطاة ، مع ترك العقدة الفرعية الموجودة في أقصى اليسار.
  • تشكل العقدة الفرعية الموجودة في أقصى اليسار قائمة مرتبطة بشكل مضاعف بجميع العقد الفرعية للعقدة الأصل ، وفي حالتنا ، الجذر الذي تم حذفه مسبقًا. سننتقل بالتسلسل إلى هذه القائمة حتى النهاية ، وبالنظر إلى العقد على أنها جذور كومة الاقتران المستقلة ، نقوم بعملية دمج العنصر الحالي للقائمة مع التالي ، مع وضع النتيجة في قائمة انتظار FIFO مُعدة مسبقًا.
  • الآن بعد تهيئة قائمة انتظار FIFO ، سنقوم بالتكرار عليها ، وننفذ عملية دمج العنصر الحالي في قائمة الانتظار مع التالي. يتم وضع نتيجة الدمج في نهاية قائمة الانتظار.
  • نكرر الخطوة السابقة حتى يظل عنصر واحد في قائمة الانتظار: كومة الاقتران الناتجة.

مثال جيد على العملية الموضحة أعلاه:

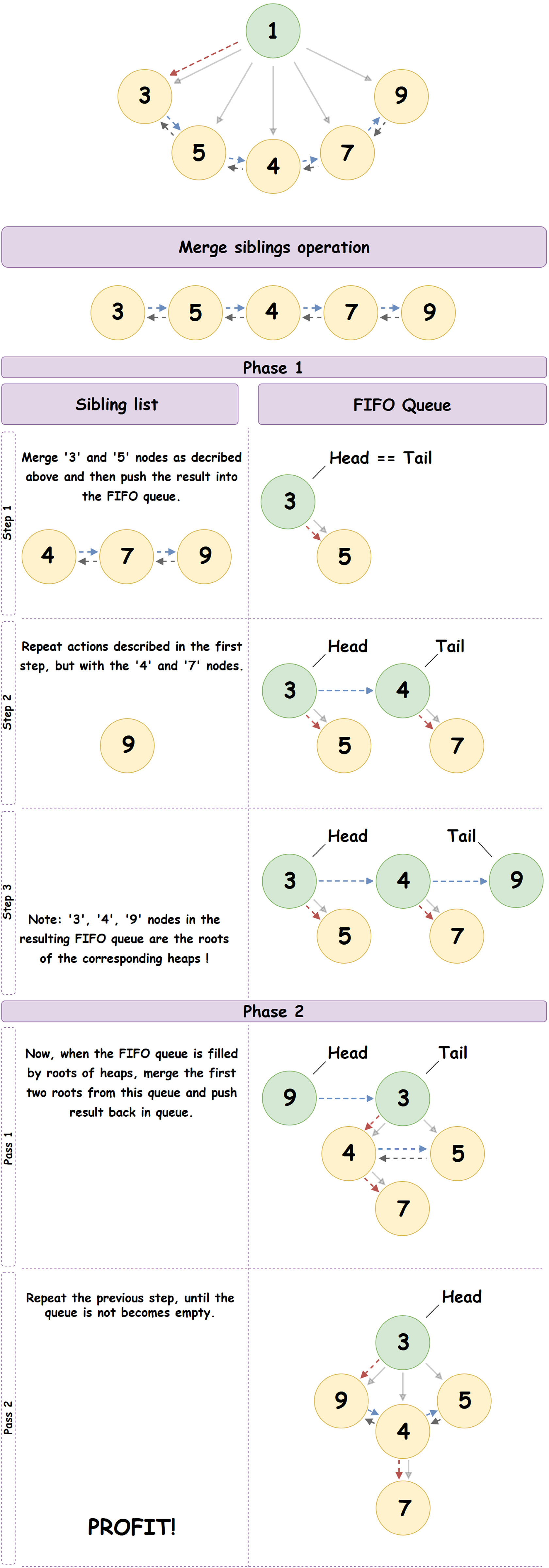
• إزالة عقدة عشوائية غير الجذر إقران كومة:
  
  خذ بعين الاعتبار العقدة المحذوفة كجذر بعض الشجرة الفرعية من كومة الذاكرة المؤقتة الأصلي. أولاً ، نقوم بإزالة جذر هذه الشجرة الفرعية ، باتباع الخوارزمية الموصوفة سابقًا لإزالة جذر كومة الاقتران ، ثم ننفذ إجراء دمج الشجرة الناتجة مع الشجرة الأصلية.
• الحصول على الحد الأدنى من عنصر كومة الاقتران:
  
  فقط قم بإرجاع قيمة جذر الكومة.

ومع ذلك ، فإن معرفتنا بـ Pairing Heap لا تنتهي عند هذا الحد: يتيح لك Pairing Heap إجراء بعض العمليات ليس على الفور ، ولكن فقط عندما تكون هناك حاجة إليها. بمعنى آخر ، يتيح لك Pairing Heap إجراء عمليات "Lazily" ، وبالتالي تخفيض التكلفة المطفأة لبعضها.
لنفترض أننا حققنا عمليات الإدراج K وحذف K في الاقتران كومة الذاكرة المؤقتة. من الواضح أن نتيجة هذه العمليات تصبح ضرورية فقط عندما نطلب الحد الأدنى من العناصر من الكومة.
دعنا نفكر في كيفية تغيير خوارزمية الإجراءات الخاصة بالعمليات الموصوفة مسبقًا أثناء تطبيق Lazy:

من خلال الاستفادة من حقيقة أن جذر Kuchi يحتوي على مؤشرين فارغين على الأقل ، سنستخدم أحدهما لتمثيل رأس قائمة مرتبطة بشكل مضاعف (المشار إليها فيما يلي بـ auxList ) من العناصر المدرجة في الكومة ، والتي سيتم اعتبار كل منها جذر كومة إقران مستقلة. ثم:

• إدراج عقدة كسول في الاقتران كومة:
  
  عند إدراج عقدة U المحددة في Pairing Heap { R_1 ، V_1 } ، نضعها في قائمة مساعدة - بعد رأس القائمة:

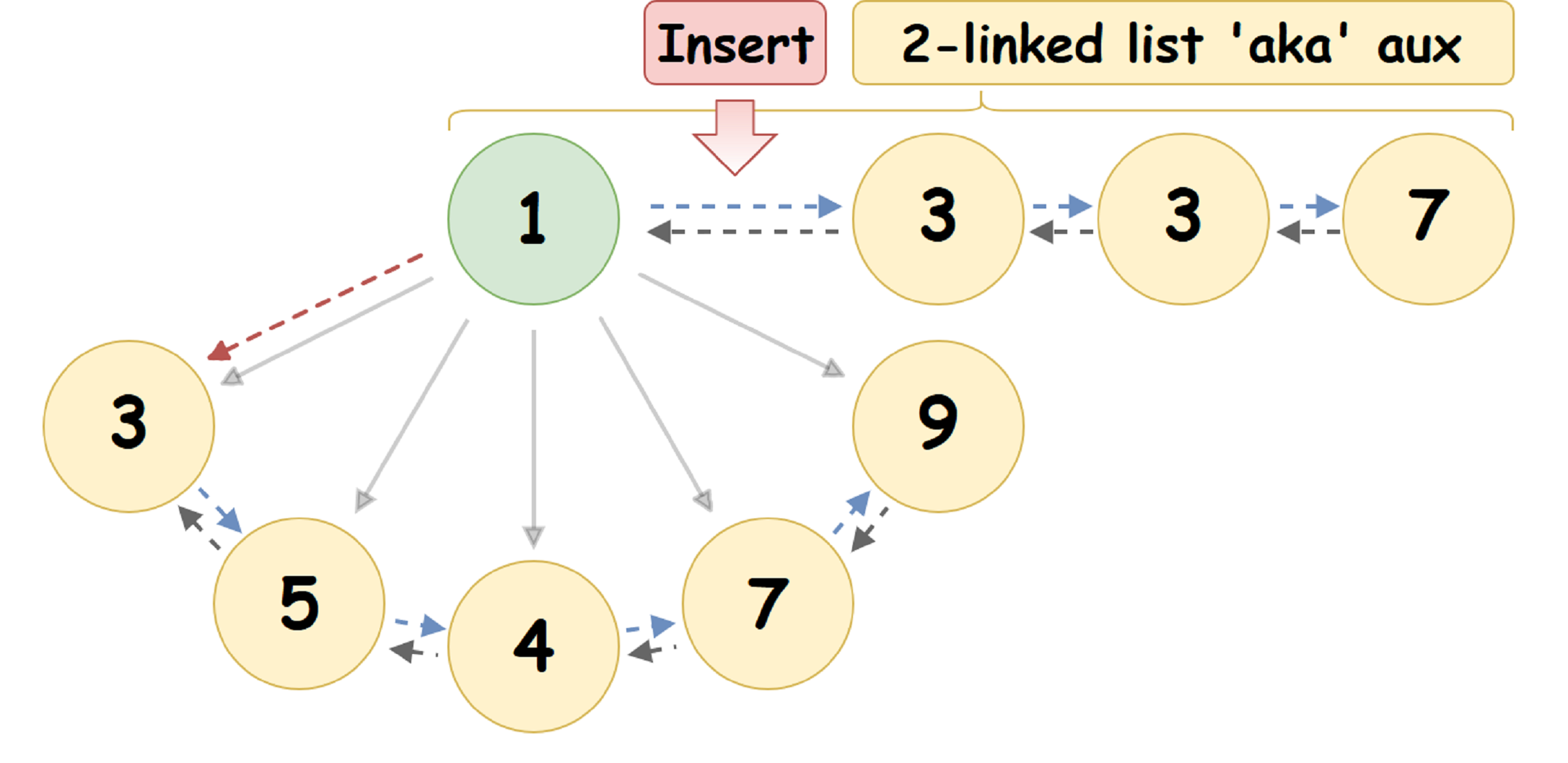
• دمج كسول اثنين من كومة الاقتران:
  
  Lazy دمج اثنين من كومة الاقتران ، على غرار إدراج عقدة Lazy ، حيث تكون العقدة المدرجة هي الجذر (رأس auxList المتصلة بشكل مضاعف) لأحد أكوام الذاكرة المؤقتة.
• كسول الحصول على الحد الأدنى من عنصر كومة الاقتران:
  
  عند طلب الحد الأدنى ، نذهب من خلال قائمة auxList إلى قائمة جذور إقران الاقتران المستقل ، مع دمج عناصر هذه القائمة مع عملية الدمج ، وإرجاع قيمة الجذر الذي يحتوي على العنصر الأدنى إلى أحد كومة الاقتران الناتجة.
• إزالة كسول للعنصر كومة الاقتران الدنيا:
  
  عند طلب إزالة الحد الأدنى للعنصر المحدد من قِبل Pairing Heap ، نجد أولاً العقدة التي تحتوي على الحد الأدنى للعنصر ، ثم نقوم بإزالته من الشجرة التي يكون فيها الجذر ، وإدراج الأشجار الفرعية الخاصة به في auxList من الكومة الرئيسية.
• إزالة كسول من عقدة كومة الاقتران غير الجذر التعسفي:
  
  عند حذف عقدة إقران كومة إجبارية غير جذرية ، تتم إزالة العقدة من الكومة ، ويتم إدراج العقد الفرعية التابعة لها في قائمة المساعدة الخاصة بكومة الذاكرة المؤقتة الرئيسية.

في الواقع ، يقلل استخدام تطبيق Lazy Pairing Heap من التكلفة المطفأة لإدخال وإزالة العقد التعسفية في Pairing Heap: من O (log N) إلى O (1).

هذا كل شيء ، ستجد أدناه قائمة بالارتباطات والموارد المفيدة:

[0] صفحة جيملوك جيثب
[1] المقال الأصلي عن الاقتران بين أكوام
[2] مقالة أصلية عن أكوام تنفيذ التزاوج
[3] قناة Telegram حول تحسين الكود ، C ++ ، Asm ، "مستوى منخفض" ولا شيء أكثر من ذلك!

أن تستمر ...