هل فكرت في تأثير أقرب مترو على سعر شقتك؟
ماذا عن العديد من رياض الأطفال حول شقتك؟ هل أنت مستعد للانغماس في عالم البيانات الجغرافية المكانية؟
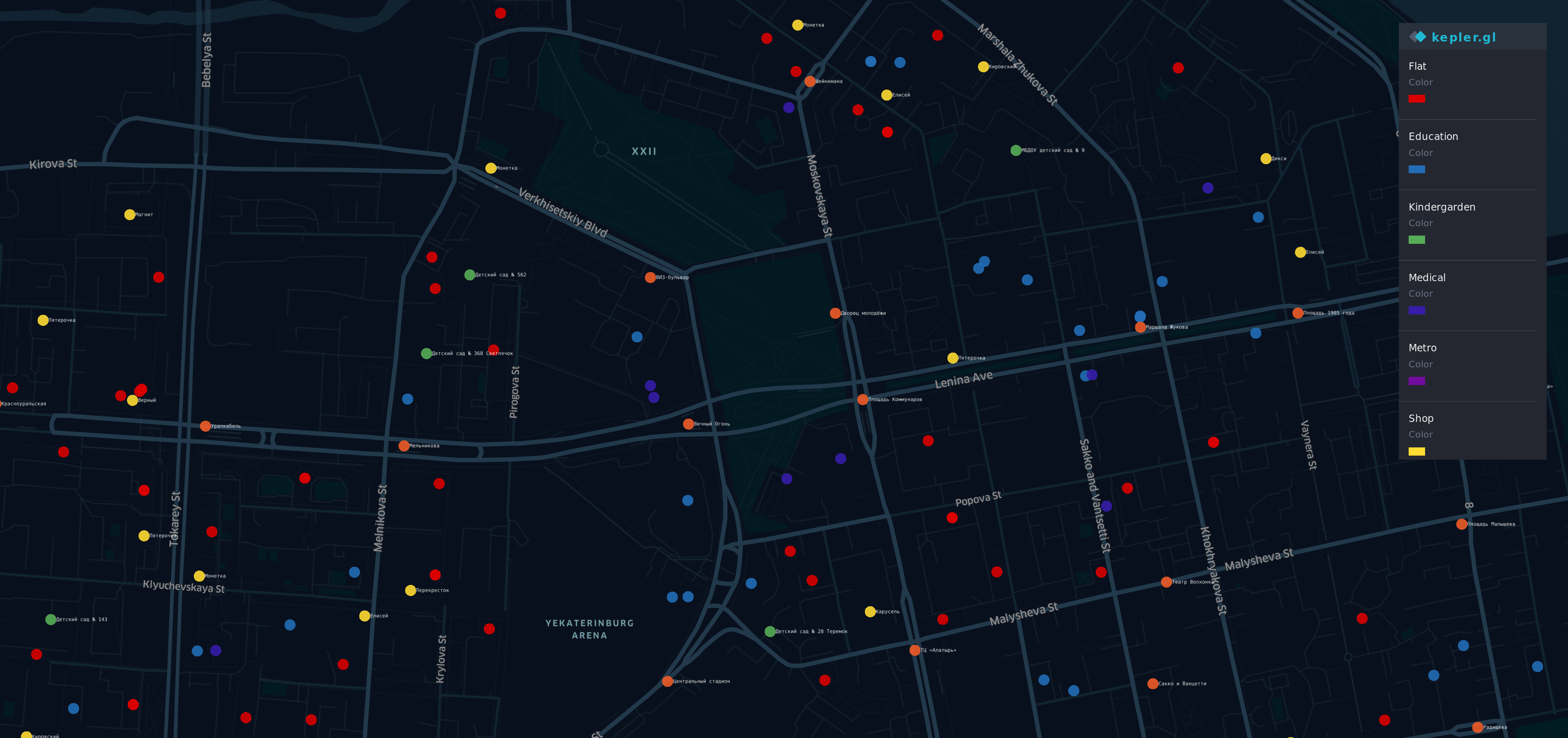
ما هو كل شيء؟
في الجزء السابق ، كان لدينا بعض البيانات وحاولنا العثور على عرض جيد بما فيه الكفاية في سوق العقارات في يكاترينبرج.
لقد وصلنا إلى نقطة عندما كان لدينا دقة في التحقق من الصحة بالقرب من 73 ٪. ومع ذلك ، كل عملة لها وجهان. ودقة 73 ٪ هو 27 ٪ من الخطأ. كيف يمكننا أن نجعل ذلك أقل؟ ما هي الخطوة التالية؟
البيانات المكانية تأتي للمساعدة
ماذا عن الحصول على المزيد من البيانات من البيئة؟ يمكننا استخدام السياق الجغرافي وبعض البيانات المكانية.
نادرا ما يقضي الناس حياتهم بأكملها في المنزل. في بعض الأحيان يذهبون إلى المتاجر ، يأخذون الأطفال من الرعاية النهارية. أطفالهم يكبرون ويذهبون إلى المدرسة والجامعة ، إلخ.
أو ... في بعض الأحيان يحتاجون إلى مساعدة طبية ويبحثون عن مستشفى. والشيء المهم للغاية هو النقل العام ، المترو على الأقل. بمعنى آخر ، هناك العديد من الأشياء القريبة منها والتي لها تأثير على التسعير.
دعني أريك قائمة منهم:
- توقف وسائل النقل العام
- محلات
- رياض الأطفال
- المستشفيات / المؤسسات الطبية
- المؤسسات التعليمية
- مترو
التصور للبيانات الجديدة
بعد الحصول على هذه المعلومات من مصادر مختلفة ، قمت بتصور.

هناك بعض النقاط على الخريطة المنطقة الأكثر شهرة (ومكلفة) في Yek aterinburg.
- R إد نقاط - الشقق
- ركض يا ge - توقف
- Y ellow - المحلات التجارية
- G رين - رياض الأطفال
- ب لوي - التعليم
- أنا ndigo - الطبية
- الخامس iolet - المترو
نعم ، قوس قزح هنا.
نظرة عامة
الآن لدينا مجموعة بيانات مرتبطة بالبيانات الجغرافية وتحتوي على بعض المعلومات الجديدة
df.head(10)

df.describe()

نموذج قديم جيد
جرب بنفس الطريقة كما كان من قبل
y = df.cost X = df.drop(columns=['cost']) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=42)
ثم نقوم بتدريب نموذجنا مرة أخرى ، ونعبر أصابعنا ونحاول التنبؤ بسعر الشقة مرة أخرى.
from sklearn.linear_model import LinearRegression regressor = LinearRegression() model = regressor.fit(X_train, y_train) do_cross_validation(X_test, y_test, model)

حسنًا ... يبدو أفضل من النتيجة السابقة بنسبة 73٪ من الدقة.
ماذا عن محاولة التفسير؟ كان لدينا نموذج سابق لديه قدرة جيدة بما فيه الكفاية لشرح السعر الثابت.
estimate_model(regressor)

عفوًا ... نموذجنا الجديد يعمل بشكل جيد مع الميزات القديمة ، لكن السلوك بميزات جديدة يبدو غريباً.
على سبيل المثال ، يؤدي العدد الأكبر من المؤسسات التعليمية أو الطبية إلى انخفاض في سعر الشقة. وفقًا لذلك ، فإن عدد نقاط الوقف القريبة المسطحة هي حالة مماثلة ويجب أن تحصل على مساهمة إضافية في السعر الثابت.
النموذج الجديد أكثر دقة ، لكنه لا يتناسب مع الحياة الحقيقية.
شيء مكسور
دع النظر في ما حدث.
بادئ ذي بدء - أود أن أذكركم بأن الميزة الرئيسية للانحدار الخطي لدينا هي ... الخطي. نعم ، الكابتن أوبيفي هو هنا.
إذا كانت بياناتك متوافقة مع فكرة "أكبر / عقد إيجار هو X فإن أكبر / إيجار سوف Y" - سيكون الانحدار الخطي أداة جيدة. لكن البيانات الجغرافية أكثر تعقيدًا مما توقعنا.
على سبيل المثال:
- عندما تكون بالقرب من شقتك هناك محطة للحافلات ، فمن الجيد ، ولكن إذا كان مقدارها حوالي 5 ، فإنه يؤدي إلى شارع صاخبة ويود الناس تجنب شراء شقة في مكان قريب.
- إذا كانت هناك جامعة ، فيجب أن يكون لها تأثير جيد على السعر ،
في الوقت نفسه ، لا يشعر حشد من الطلاب بالقرب من منزلك بالسعادة إذا لم تكن شخصًا اجتماعيًا للغاية. - مترو بالقرب من منزلك أمر جيد ، ولكن إذا كنت تعيش في ساعة واحدة سيرا على الأقدام
من أقرب مترو - لا ينبغي أن يكون له معنى.
كما ترى - يعتمد ذلك على العديد من العوامل ووجهات النظر. وطبيعة بياناتنا الجغرافية ليست خطية ، لا يمكننا استقراء تأثيرها.
في الوقت نفسه ، لماذا يعمل النموذج مع المعاملات الغريبة بشكل أفضل من السابق؟
plot.figure(figsize=(10,10)) corr = df.corr()*100.0 sns.heatmap(corr[['cost']], cmap= sns.diverging_palette(220, 10), center=0, linewidths=1, cbar_kws={"shrink": .7}, annot=True, fmt=".2f")

تبدو مثيرة للاهتمام. لقد رأينا صورة مماثلة في الجزء السابق.
هناك علاقة سلبية بين المسافة إلى أقرب مترو والسعر. وهذا العامل له تأثير على الدقة أكثر من بعض العوامل القديمة.
وفي الوقت نفسه ، عمل نموذجنا فوضوي ولا يرى التبعيات بين البيانات المجمعة والمتغير الهدف. بساطة الانحدار الخطي له حدوده الخاصة.
الملك ميت ، يحيا الملك!
وإذا كان الانحدار الخطي غير مناسب لحالتنا ، فما الذي يمكن أن يكون أفضل؟ إذا كان نموذجنا فقط "أكثر ذكاء" ...
لحسن الحظ ، لدينا نهج يجب أن يكون أفضل بسببه ... أكثر مرونة ولديه آلية مضمنة "تفعل ذلك إذا فعل ذلك بفعل ذلك".
شجرة القرار تظهر على الساحة.
from sklearn.tree import DecisionTreeRegressor A decision tree can have a different depth, usually, it works well when depth is 3 and bigger. And the parameter of max depth has the biggest influence on the result. Let's do some code for checking depth from 3 to 32 data = [] for x in range(3,32): regressor = DecisionTreeRegressor(max_depth=x,random_state=42) model = regressor.fit(X_train, y_train) accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) ax = sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ')

حسنا ... لحالة عندما م Ax_depth من شجرة تساوي 8 دقة أعلى من 77.
وسيكون إنجازًا جيدًا إذا لم نفكر في حدود هذا النهج. دعنا نلقي نظرة على كيف ستعمل ax_depht = 2
from IPython.core.display import Image, SVG from sklearn.tree import export_graphviz from graphviz import Source 2_level_regressor = DecisionTreeRegressor(max_depth=2, random_state=42) model = 2_level_regressor.fit(X_train, y_train) graph = Source(export_graphviz(model, out_file=None , feature_names=X.columns , filled = True)) SVG(graph.pipe(format='svg'))

في هذه الصورة ، يمكننا أن نرى أن هناك 4 أنواع فقط من التنبؤ. عند استخدام DecisionTreeRegressor ، فإنه يعمل بشكل مختلف عن الانحدار الخطي . فقط بطريقة مختلفة. لا يستخدم مساهمة من العوامل (المعاملات) ، بدلاً من ذلك يستخدم DecisionTreeRegressor "الاحتمال". وسعر شقة سيكون هو نفسه لديه شقة الأكثر مماثلة على التنبؤ.
يمكننا أن نظهر ذلك من خلال التنبؤ سعرنا مع تلك الشجرة.
y = two_level_regressor.predict(X_test) errors = pd.DataFrame(data=y,columns=['errors']) f, ax = plot.subplots(figsize=(12, 12)) sns.countplot(x="errors", data=errors)

وكل التنبؤ الخاص بك سوف تتطابق مع واحدة من هذه القيم. وعندما نستخدم max_depth = 8 ، لا يمكننا أن نتوقع أكثر من 256 خيارًا مختلفًا لأكثر من 2000 شقة. ربما يكون هذا مفيدًا لقضايا التصنيف ، لكنه ليس مرنًا بما يكفي لقضيتنا.
حكمة الحشد
إذا حاولت التنبؤ بالنتيجة في نهائي كأس العالم - فهناك احتمال كبير بأنك مخطئ. في الوقت نفسه ، إذا طلبت رأي جميع القضاة في البطولة - سيكون لديك فرص أفضل للتخمين. إذا سألت خبراء مستقلين ومدربين وقضاة ثم أجرينا بعض الإجابات السحرية - فستزيد فرصتك بشكل كبير. يبدو وكأنه انتخاب رئيس.
مجموعة من العديد من الأشجار "البدائية" يمكن أن تعطي أكثر من كل منها. وراندو mForestRegressor هو أداة التي سوف نستخدمها
بادئ ذي بدء ، دعونا ننظر في العوامل الأساسية - max_depth ، max_features وعدد من الأشجار في النموذج.
عدد الاشجار
وفقًا لـ "كم شجرة في غابة عشوائية؟" الخيار الأفضل سيكون 128 شجرة . زيادة عدد الأشجار لا تؤدي إلى تحسن كبير في الدقة ، ولكن زيادة وقت التدريب.
أقصى عدد من الميزات
الآن لدينا نموذج يحتوي على 12 الميزات. نصفهم من تلك القديمة التي ترتبط مع ميزات شقة ، وغيرها تتعلق السياق الجغرافي. لذلك قررت إعطاء فرصة لكل منهم. فليكن 6 ميزات لشجرة.
أقصى عمق الشجرة
لهذه المعلمة ، يمكننا تحليل منحنى التعلم.
from sklearn.ensemble import RandomForestRegressor data = [] for x in range(1,32): regressor = RandomForestRegressor(random_state=42, max_depth=x, n_estimators=128,max_features=6)model = regressor.fit(X_train, y_train)accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) f, ax = plot.subplots(figsize=(10, 10)) sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ') from sklearn.ensemble import RandomForestRegressor data = [] for x in range(1,32): regressor = RandomForestRegressor(random_state=42, max_depth=x, n_estimators=128,max_features=6)model = regressor.fit(X_train, y_train)accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) f, ax = plot.subplots(figsize=(10, 10)) sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ') from sklearn.ensemble import RandomForestRegressor data = [] for x in range(1,32): regressor = RandomForestRegressor(random_state=42, max_depth=x, n_estimators=128,max_features=6)model = regressor.fit(X_train, y_train)accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) f, ax = plot.subplots(figsize=(10, 10)) sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ')

قف ... دقة أكثر من 86 ٪ على max_depth = 16 مقابل 77 ٪ على شجرة تصميم واحدة. يبدو مذهلا ، أليس كذلك؟
استنتاج
حسنًا ... لدينا الآن نتيجة أفضل من التنبؤات السابقة ، 86٪ بالقرب من خط النهاية. الخطوة الأخيرة للتحقق - دعنا ننظر إلى أهمية الميزة. هل أعطت البيانات الجغرافية أي فائدة لنموذجنا؟
feat_importances = model.feature_importances_ feat_importances = pd.Series(feat_importances, index=X.columns) feat_importances.nlargest(5).plot(kind='barh')

لا تزال بعض الميزات القديمة تؤثر على النتيجة. في الوقت نفسه أثرت المسافة إلى أقرب مترو ورياض الأطفال. وهذا يبدو منطقيا.
دون شك ، ساعدتنا البيانات الجغرافية في تحسين نموذجنا.
شكرا للقراءة!
PS
رحلتنا لم تنته بعد. دقة 86 ٪ هي نتيجة هائلة للبيانات الحقيقية. وفي الوقت نفسه ، هناك فجوة صغيرة بين 14 ٪ و 10 ٪ من الخطأ المتوسط ، والذي نتوقعه. في الفصل التالي من قصتنا ، سنحاول التغلب على هذا الحاجز أو على الأقل لتقليل هذا الخطأ.
هناك دفتر IPython