🛍️ 👷🏼 💀 معادلة Navier-Stokes ومحاكاة السوائل على CUDA 🌙 😈 🙌

مرحبا يا هبر. في هذه المقالة ، سنتعامل مع معادلة Navier-Stokes لسائل غير قابل للضغط ، ونحلها رقميًا ، ونجري محاكاة جميلة تعمل عن طريق الحوسبة المتوازية على CUDA. الهدف الرئيسي هو إظهار كيف يمكنك تطبيق الرياضيات التي تقوم عليها المعادلة في الممارسة العملية عند حل مشكلة نمذجة السوائل والغازات.

تحذير

تحتوي المقالة على الكثير من الرياضيات ، لذلك يمكن للراغبين في الجانب الفني من المشكلة الانتقال مباشرةً إلى قسم التنفيذ في الخوارزمية. ومع ذلك ، ما زلت أوصي بأن تقرأ المقالة بأكملها وتحاول فهم مبدأ الحل. إذا كانت لديك أية أسئلة بنهاية القراءة ، فسيسعدني أن أجيب عليها في التعليقات على المنشور.

ملاحظة: إذا كنت تقرأ حبر من جهاز محمول ، ولم تشاهد الصيغ ، فاستخدم النسخة الكاملة للموقع

معادلة Navier-Stokes لسائل غير قابل للضغط

ج ز ئ ي ة أ ك ث ر م ن ج ز ئ ي ة

${\ جزئية {\ bf \ vec {u}} \ أكثر من {\ جزئية t}} = - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} - {1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$

أعتقد أن الجميع قد سمعوا مرة واحدة على الأقل عن هذه المعادلة ، بعضها ، وربما حلها بشكل تحليلي في حالاتها الخاصة ، لكن بشكل عام ، تظل هذه المشكلة دون حل حتى الآن. بالطبع ، نحن لا نضع هدفًا لحل مشكلة الألفية في هذه المقالة ، ومع ذلك لا يزال بإمكاننا تطبيق الطريقة التكرارية عليها. ولكن بالنسبة للمبتدئين ، دعونا ننظر إلى التدوين في هذه الصيغة.

تقليديًا ، يمكن تقسيم معادلة Navier-Stokes إلى خمسة أجزاء:

$\ جزئية {\ bf \ vec {u}} \ over \ جزئية t$ - يدل على معدل التغير في سرعة المائع عند نقطة (سننظر في كل جسيم في محاكاة لدينا).
$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}}$ - حركة السوائل في الفضاء.
$- {1 \ over \ rho} \ nabla {\ bf p}$ هو الضغط الذي يمارس على الجسيمات (هنا $\ rho$ - معامل كثافة السوائل).
$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - لزوجة الوسيط (كلما زاد حجمها ، كلما كان السائل يقاوم القوة المطبقة من جانبه) ، $\ nu$ - معامل اللزوجة).
$\ bf \ vec {F}$ - القوى الخارجية التي نطبقها على السائل (في حالتنا ، ستلعب القوة دورًا محددًا للغاية - ستعكس الإجراءات التي يقوم بها المستخدم.

أيضًا ، نظرًا إلى أننا سننظر في حالة سائل غير متجانس وغير قابل للضغط ، لدينا معادلة أخرى:

${{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ . الطاقة في البيئة ثابتة ، لا تذهب إلى أي مكان ، لا تأتي من أي مكان.

سيكون من الخطأ حرمان جميع القراء الذين لم يكونوا على دراية بتحليل المتجهات ، وبالتالي ، في نفس الوقت ، واستعرض باختصار جميع المشغلين الموجودين في المعادلة (ومع ذلك ، فإنني أوصي بشدة بتذكير ما هو المشتق والتفاضلي والمتجه ، لأنهم يرتكزون على كل ذلك ما سوف تناقش أدناه).

نبدأ بمشغل nabla ، الذي يمثل ناقلًا (في حالتنا ، سيكون مكونًا من عنصرين ، نظرًا لأننا سنقوم بنمذجة السائل في الفضاء ثنائي الأبعاد):

$\ nabla = {\ تبدأ {pmatrix} {\ جزئية \ فوق \ جزئية x} ، {\ جزئية \ فوق \ جزئية y} \ end {pmatrix}}$

عامل nabla هو عامل تفاضلي متجه ويمكن تطبيقه على كل من دالة العددية وعلى متجه واحد. في حالة العددية ، نحصل على التدرج اللوني للوظيفة (متجه مشتقاته الجزئية) ، وفي حالة المتجه ، مجموع المشتقات الجزئية على طول المحاور. الميزة الرئيسية لهذا المشغل هي أنه من خلاله يمكنك التعبير عن العمليات الرئيسية لتحليل المتجهات - grad ( gradient ) ، div ( divergence ) ، rot ( rototor ) و

$\ nabla ^ 2$ ( مشغل لابلاس ). تجدر الإشارة على الفور إلى أن التعبير

$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {u}}$ لا يرقى إلى

$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {u}}$ - عامل nabla لا يملك تبديلية.

كما سنرى لاحقًا ، يتم تبسيط هذه التعبيرات بشكل ملحوظ عند الانتقال إلى مساحة منفصلة سننفذ فيها جميع الحسابات ، لذلك لا تنزعج إذا لم تكن واضحًا في الوقت الحالي بشأن ما يجب القيام به مع كل هذا. بعد تقسيم المهمة إلى عدة أجزاء ، سنحل كل منها على التوالي ونعرض كل ذلك في شكل تطبيق متتابع لعدة وظائف على بيئتنا.

الحل العددي لمعادلة Navier-Stokes

لتمثيل سائلنا في البرنامج ، نحتاج إلى الحصول على تمثيل رياضي لحالة كل جسيم سائل في وقت تعسفي. الطريقة الأكثر ملاءمة لذلك هي إنشاء حقل متجه من الجزيئات يخزن حالته في شكل مستوي إحداثي:

في كل خلية من صفيفنا ثنائي الأبعاد ، سنخزن سرعة الجسيمات في وقت واحد

$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}، t)، \ bf \ vec {x} = \ تبدأ {pmatrix} x، y \ end {pmatrix}$ ، والمسافة بين الجزيئات هي التي يرمز لها

$\ دلتا ×$ و

$\ دلتا ذ$ على التوالي. في الكود ، سيكون كافياً بالنسبة لنا تغيير قيمة السرعة لكل تكرار ، وحل مجموعة من المعادلات المتعددة.

الآن نعبر عن التدرج والانحراف ومشغل لابلاس مع مراعاة شبكة الإحداثيات لدينا (

$i، j$ - المؤشرات في الصفيف ،

$\ bf \ vec {u} _ {(x)} ، \ vec {u} _ {(y)}$ - أخذ المكونات المقابلة من المتجه):

عامل	تعريف	منفصلة التناظرية
غراد	$\ nabla \ bf p = \ تبدأ {pmatrix} {\ جزئية \ bf p \ over \ جزئية x} ، {\ جزئية \ bf p \ over \ جزئية y} \ end {pmatrix}$	${{p_ {i + 1، j}} - {p_ {i - 1، j}} \ over {2 \ delta x}}، {{p_ {i، j + 1}} - {p_ {i، j - 1}} \ over {2 \ delta y}}$
شعبة	$\ nabla \ cdot \ bf \ vec {u} = {{\ جزئية u \ over \ جزئية x} + {\ جزئية u \ over \ جزئية y}}$	${{\ \ vec {u} _ {(x) i + 1، j} - \ vec {u} _ {(x) i - 1، j}} \ over {2 \ delta x}} + {{\ vec {u} _ {(y) i، j + 1} - \ vec {u} _ {(y) i، j - 1}} \ over {2 \ delta y}}$
$\ bf \ Delta$	$\ bf \ nabla ^ 2p = {\ جزئية ^ 2 p \ over \ جزئية x ^ 2} + + {\ جزئية ^ 2 p \ over \ جزئية y ^ 2}$	${{p_ {i + 1، j} -2p_ {i، j} + p_ {i - 1، j}} \ over (\ delta x) ^ 2} + {{p_ {i، j + 1} - 2p_ {i، j} + p_ {i، j - 1}} \ over (\ delta y) ^ 2}$
تعفن	$\ bf \ nabla \ times \ vec {u} = {{\ جزئية \ vec {u} \ over \ جزئية y} - {\ جزئية \ vec {u} \ over \ جزئية x}}$	${\ vec {u} _ {(y) i، j + 1} - \ vec {u} _ {(y) i، j - 1} \ over 2 \ delta y} - {\ vec {u} _ {(x) i + 1، j} - \ vec {u} _ {(x) i - 1، j} \ over 2 \ delta x}$

يمكننا تبسيط الصيغ المنفصلة لمشغلي المتجهات إذا افترضنا ذلك

$\ delta x = \ delta y = 1$ . لن يؤثر هذا الافتراض بشكل كبير على دقة الخوارزمية ، ومع ذلك ، فهو يقلل من عدد العمليات لكل تكرار ، ويجعل التعبيرات بشكل عام أكثر متعة للعين.

حركة الجسيمات

هذه العبارات لا تعمل إلا إذا تمكنا من العثور على أقرب الجسيمات بالنسبة للجسيم قيد الدراسة في الوقت الحالي. من أجل إلغاء جميع التكاليف المحتملة المرتبطة بالعثور عليها ، فإننا لن نتتبع حركتها ، ولكن من أين تأتي الجزيئات في بداية التكرار من خلال إسقاط مسار الحركة للخلف في الوقت المناسب (وبعبارة أخرى ، قم بطرح متجه السرعة مرات تغيير الوقت من الموقف الحالي). باستخدام هذه التقنية لكل عنصر من عناصر المصفوفة ، سنكون متأكدين من أن أي جسيم سيكون له "جيران":

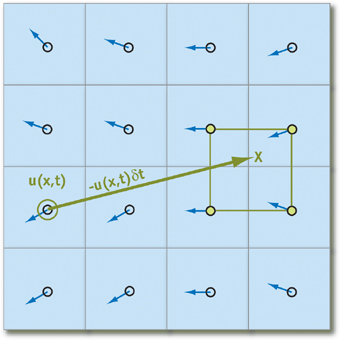
وضع ذلك

$ف دولا$ - عنصر صفيف يخزن حالة الجسيمات ، نحصل على الصيغة التالية لحساب حالتها بمرور الوقت

$\ دلتا ر$ (نعتقد أن جميع المعلمات اللازمة في شكل التسارع والضغط قد تم حسابها بالفعل):

$q ({{\ \ vec {\ bf x}} ، t + \ delta t}) = q ({{\ \ bf \ vec {x}} - {\ bf \ vec {u}} \ delta t}، t)$

نلاحظ على الفور أنه صغير بما فيه الكفاية

$\ دلتا ر$ ولا يمكننا أبدًا تجاوز حدود الخلية ، لذلك من المهم جدًا اختيار الزخم المناسب الذي سيعطيه المستخدم للجزيئات.

من أجل تجنب فقدان الدقة في حالة حدوث إسقاط في حدود الخلية أو في حالة إحداثيات غير عدد صحيح ، سنقوم بإجراء استيفاء خطي مزدوج لحالات الجسيمات الأقرب الأربعة ونأخذها كقيمة حقيقية في هذه النقطة. من حيث المبدأ ، لن تقلل مثل هذه الطريقة من الناحية العملية من دقة المحاكاة ، وفي نفس الوقت يكون التنفيذ بسيطًا للغاية ، لذلك سنستخدمها.

لزوجة

كل سائل له لزوجة معينة ، والقدرة على منع تأثير القوى الخارجية على أجزائه (العسل والماء سيكونان مثالاً جيدًا ، وفي بعض الحالات تختلف معاملات اللزوجة حسب الحجم). تؤثر اللزوجة بشكل مباشر على التسارع الذي يكتسبه السائل ، ويمكن التعبير عنه بالصيغة أدناه ، إذا كنا نختصر المصطلحات الأخرى لفترة قصيرة:

${\ جزئية \ vec {\ bf u} \ over \ جزئية t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$

. في هذه الحالة ، تأخذ المعادلة التكرارية للسرعة بالشكل التالي:

$u ({\ bf \ vec {x}}، t + \ delta t) = u ({\ bf \ vec {x}}، t) + \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$

سوف نقوم بتحويل هذه المساواة قليلاً ، ونصل بها إلى الشكل

$\ bf A \ vec {x} = \ vec {b}$ (النموذج القياسي لنظام المعادلات الخطية):

$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}، t + \ delta t) = {u ({\ bf \ vec {x}}، t )}$

حيث

$\ bf I$ هي مصفوفة الهوية. نحن بحاجة إلى مثل هذه التحولات من أجل تطبيق طريقة جاكوبي فيما بعد لحل عدة أنظمة مماثلة للمعادلات. سنناقشها لاحقًا.

قوى خارجية

أبسط خطوة في الخوارزمية هي تطبيق القوى الخارجية على الوسيط. بالنسبة للمستخدم ، سينعكس هذا في شكل نقرات على الشاشة باستخدام الماوس أو حركته. يمكن وصف القوة الخارجية بالمعادلة التالية ، والتي نطبقها على كل عنصر من عناصر المصفوفة (

$\ vec {\ bf G}$ - متجه الزخم

$x_p ، y_p$ - موقف الماوس

$x ، y$ - إحداثيات الخلية الحالية ،

$ص$ - نصف قطر العمل ، معلمة القياس):

$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \ left (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} \ over r} \ اليمين)$

يمكن حساب متجه النبض بسهولة كالفرق بين الموضع السابق للماوس والموضع الحالي (إذا كان هناك واحد) ، وهنا لا يزال بإمكانك أن تكون مبدعًا. في هذا الجزء من الخوارزمية يمكننا تقديم إضافة الألوان إلى سائل ، وإضاءة ، وما إلى ذلك. يمكن أن تشمل القوى الخارجية أيضًا الجاذبية ودرجة الحرارة ، وعلى الرغم من أنه ليس من الصعب تنفيذ مثل هذه المعلمات ، إلا أننا لن نعتبرها في هذه المقالة.

الضغط

الضغط في معادلة Navier-Stokes هو القوة التي تمنع الجزيئات من ملء كل المساحة المتاحة لها بعد تطبيق أي قوة خارجية عليها. على الفور ، حسابها صعب للغاية ، ولكن يمكن تبسيط مشكلتنا إلى حد كبير من خلال تطبيق نظرية تحلل Helmholtz .

ونحن ندعو

$\ bf \ vec {W}$ مجال مكافحة ناقلات التي تم الحصول عليها بعد حساب النزوح والقوى الخارجية واللزوجة. سيكون هناك تباعد غير صفري ، مما يتناقض مع حالة عدم انضغاط السائل (

$\ nabla \ cdot \ bf \ vec {u} = 0$ ) ، ولإصلاح ذلك ، من الضروري حساب الضغط. وفقًا لنظرية تحلل هلمهولتز ،

$\ bf \ vec {W}$ يمكن تمثيله كمجموع مجالين:

$\ bf \ vec {W} = \ vec {u} + \ nabla p$

حيث

$\ bf u$ - هذا هو مجال مكافحة ناقلات الذي نبحث عنه مع اختلاف التباعد. لن يتم تقديم أي دليل على هذه المساواة في هذه المقالة ، ولكن في النهاية يمكنك العثور على رابط مع شرح مفصل. يمكننا تطبيق عامل nabla على كلا جانبي التعبير للحصول على الصيغة التالية لحساب مجال ضغط العدد:

$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p$

التعبير المكتوب أعلاه هو معادلة بواسون للضغط. يمكننا أيضًا حلها عن طريق طريقة Jacobi المذكورة آنفًا ، وبالتالي نجد آخر متغير غير معروف في معادلة Navier-Stokes. من حيث المبدأ ، يمكن حل أنظمة المعادلات الخطية بعدة طرق مختلفة ومعقدة ، لكننا سنظل نتناول أبسطها ، حتى لا نثقل كاهل هذه المقالة.

الشروط الحدودية و الأولية

تتطلب أي معادلة تفاضلية تم تصميمها على نطاق محدود شروطًا أولية أو حدودية محددة بشكل صحيح ، وإلا فمن المحتمل جدًا أن نحصل على نتيجة غير صحيحة جسديًا. يتم تحديد شروط الحدود للتحكم في سلوك المائع بالقرب من حواف شبكة الإحداثيات ، وتحدد الشروط الأولية المعلمات التي لدى الجسيمات في وقت بدء البرنامج.

ستكون الشروط الأولية بسيطة للغاية - في البداية يكون السائل ثابتًا (سرعة الجسيمات صفر) ، والضغط أيضًا صفر. سيتم تعيين شروط الحدود للسرعة والضغط بواسطة الصيغ المعطاة:

${\ bf \ vec {u} _ {0، j} + \ bf \ vec {u} _ {1، j} \ over 2 \ delta y} = 0، {\ bf \ vec {u} _ {i ، 0} + \ bf \ vec {u} _ {i، 1} \ over 2 \ delta x} = 0$

${\ bf p_ {0، j} - \ bf p_ {1، j} \ over \ delta x} = 0، {\ bf p_ {i، 0} - \ bf p_ {i، 1} \ over \ delta ذ} = 0 دولا$

وبالتالي ، فإن سرعة الجسيمات عند الحواف ستكون عكس السرعة في الحواف (وبالتالي فإنها سوف تتصدى من الحافة) ، ويكون الضغط مساويًا للقيمة المجاورة للحدود مباشرةً. يجب تطبيق هذه العمليات على جميع العناصر المرتبطة للصفيف (على سبيل المثال ، هناك حجم شبكة

$N \ مرة M$ ، ثم نطبق الخوارزمية للخلايا المميزة باللون الأزرق في الشكل):

صبغ

مع ما لدينا الآن ، يمكنك بالفعل التوصل إلى الكثير من الأشياء المثيرة للاهتمام. على سبيل المثال ، لتحقيق انتشار الصبغة في السائل. للقيام بذلك ، نحتاج فقط إلى الحفاظ على حقل عددي آخر ، والذي سيكون مسؤولاً عن مقدار الطلاء في كل نقطة من المحاكاة. الصيغة لتحديث الصبغة تشبه إلى حد كبير السرعة ، ويتم التعبير عنها على النحو التالي:

${\ جزئية d \ over \ جزئية t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gamma \ nabla ^ 2d + S$

في الصيغة

$S$ مسؤول عن تجديد المنطقة بصبغة (ربما حسب المكان الذي ينقر فيه المستخدم) ،

$د$ مباشرة هي كمية الصبغة في هذه النقطة ، و

$\ gamma$ - معامل الانتشار. حلها ليس بالأمر الصعب ، حيث أن جميع الأعمال الأساسية المتعلقة باشتقاق الصيغ قد تم تنفيذها بالفعل ، وهي كافية لإجراء بعض البدائل. يمكن تنفيذ الرسام في الكود بلون في تنسيق RGB ، وفي هذه الحالة يتم تقليل المهمة إلى عمليات مع العديد من القيم الحقيقية.

الدردورية

لا تعد معادلة الدوامة جزءًا مباشرًا من معادلة Navier-Stokes ، ولكنها تعد معلمة مهمة لمحاكاة معقولة لحركة الصبغة في السائل. نظرًا لحقيقة أننا ننتج خوارزمية في حقل منفصل ، وكذلك بسبب الخسائر في دقة قيم الفاصلة العائمة ، يتم فقد هذا التأثير ، وبالتالي نحتاج إلى استعادته عن طريق تطبيق قوة إضافية على كل نقطة في الفضاء. تم تحديد متجه هذه القوة كـ

$\ bf \ vec {T}$ ويتم تحديده بواسطة الصيغ التالية:

$\ bf \ omega = \ nabla \ times \ vec {u}$

$\ vec {\ eta} = \ nabla | \ omega |$

$\ bf \ vec {\ psi} = {\ vec {\ eta} \ over {| \ vec {\ eta} |}}$

$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ times \ omega) \ delta x$

$\ أوميغا$ هناك نتيجة لتطبيق الدوار على ناقل السرعة (يرد تعريفه في بداية المقال) ،

$\ vec \ eta$ - التدرج في مجال العددية للقيم المطلقة

$\ أوميغا$ .

$\ vec \ psi$ يمثل ناقل طبيعي

$\ vec \ eta$ و

$\ epsilon$ هو ثابت يتحكم في حجم الدوامات في سائلنا.

طريقة جاكوبي لحل أنظمة المعادلات الخطية

عند تحليل معادلات Navier-Stokes ، توصلنا إلى نظامين من المعادلات - أحدهما يتعلق باللزوجة والآخر للضغط. يمكن حلها بواسطة خوارزمية تكرارية ، يمكن وصفها بواسطة الصيغة التكرارية التالية:

$x ^ {(k + 1)} _ {i، j} = {{x ^ {(k)} _ {i-1، j} + x ^ {(k)} _ {i + 1، j} + x ^ {(k)} _ {i، j-1} + x ^ {(k)} _ {i، j + 1} + \ alpha b_ {i، j}} \ over \ beta}$

بالنسبة لنا

$x$ - عناصر مجموعة تمثل حقل العددية أو المتجهات.

$ك$ - رقم التكرار ، يمكننا ضبطه من أجل زيادة دقة الحساب أو العكس بالعكس لتقليله وزيادة الإنتاجية.

لحساب اللزوجة نستبدل:

$x = b = \ bf \ vec {u}$ .

$\ alpha = {1 \ over \ nu \ delta t}$ .

$\ beta = 4+ \ alpha$ ، هنا المعلمة

$\ beta$ - مجموع الأوزان. وبالتالي ، نحتاج إلى تخزين حقلي سرعة متجهين على الأقل من أجل قراءة قيم أحد الحقول بشكل مستقل وكتابتها في حقل آخر. في المتوسط ، لحساب مجال السرعة باستخدام طريقة Jacobi ، من الضروري إجراء 20 إلى 50 تكرارًا ، وهذا كثير جدًا إذا أجرينا حسابات على وحدة المعالجة المركزية.

لمعادلة الضغط ، نقوم بالتبديل التالي:

$x = p$ .

$b = \ nabla \ bf \ cdot \ vec {W}$ .

$\ alpha = -1$ .

$\ beta = 4$ . نتيجة لذلك ، نحصل على القيمة

$p_ {i، j} \ delta t$ عند هذه النقطة. ولكن نظرًا لأنه يستخدم فقط لحساب التدرج المخصوم من حقل السرعة ، يمكن حذف التحويلات الإضافية. بالنسبة لحقل الضغط ، من الأفضل إجراء 40-80 تكرارًا ، لأنه مع وجود أعداد أقل يصبح التناقض ملحوظًا.

تنفيذ الخوارزمية

سننفذ الخوارزمية في C ++ ، نحتاج أيضًا إلى Cuda Toolkit (يمكنك قراءة كيفية تثبيته على موقع Nvidia) ، وكذلك SFML . نحتاج إلى CUDA لموازنة الخوارزمية ، وسيتم استخدام SFML فقط لإنشاء نافذة وعرض صورة على الشاشة (من حيث المبدأ ، يمكن كتابة هذا في OpenGL ، ولكن الفرق في الأداء سيكون ضئيلًا ، لكن الكود سيزداد بمقدار 200 سطر آخر).

مجموعة أدوات Cuda

أولاً ، سنتحدث قليلاً عن كيفية استخدام Cuda Toolkit لموازنة المهام. يتم توفير دليل أكثر تفصيلا من قبل نفيديا نفسها ، لذلك نحن هنا نقتصر فقط على الأكثر ضرورة. من المفترض أيضًا أنك تمكنت من تثبيت برنامج التحويل البرمجي ، وكنت قادراً على إنشاء مشروع اختبار دون أخطاء.

لإنشاء وظيفة يتم تشغيلها على وحدة معالجة الرسومات ، يجب أولاً أن تعلن عن عدد النواة التي نرغب في استخدامها ، وعدد كتل النواة التي نحتاج إلى تخصيصها. لهذا ، توفر لنا مجموعة Cuda Toolkit بنية خاصة - dim3 ، من خلال إعداد كل قيم x و y و z الافتراضية على 1. عن طريق تحديدها كوسيطة عند استدعاء الوظيفة ، يمكننا التحكم في عدد النواة المخصصة. نظرًا لأننا نعمل مع صفيف ثنائي الأبعاد ، نحتاج إلى تعيين حقلين فقط في المُنشئ: x و y :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads);

حيث size_x و size_y هما حجم المصفوفة قيد المعالجة. استدعاء الدالة والتوقيع كالتالي (تتم معالجة الأقواس ثلاثية الزاوية بواسطة برنامج التحويل البرمجي Cuda):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host

في الوظيفة نفسها ، يمكنك استعادة مؤشرات صفيف ثنائي الأبعاد من خلال رقم الكتلة ورقم النواة في هذه الكتلة باستخدام الصيغة التالية:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y;

تجدر الإشارة إلى أن الوظيفة المنفذة على بطاقة الفيديو يجب أن يتم وضع علامة عليها بعلامة __global__ ، وأن تُرجع أيضًا لاغية ، لذلك غالبًا ما تتم كتابة نتائج العمليات الحسابية على المصفوفة التي تم تمريرها كوسيطة وتم تخصيصها مسبقًا في ذاكرة بطاقة الفيديو.

وظائف CudaMalloc و CudaFree هي المسؤولة عن تحرير وتخصيص الذاكرة على بطاقة الفيديو. يمكننا العمل على مؤشرات إلى منطقة الذاكرة التي يعودون إليها ، لكن لا يمكننا الوصول إلى البيانات من الكود الرئيسي. أسهل طريقة لإرجاع نتائج الحساب هي استخدام cudaMemcpy ، على غرار memcpy القياسي ، لكن مع إمكانية نسخ البيانات من بطاقة الفيديو إلى الذاكرة الرئيسية والعكس.

SFML ونافذة تقديم

مسلحين بكل هذه المعرفة ، يمكننا أخيرًا الانتقال إلى كتابة التعليمات البرمجية مباشرةً. للبدء ، دعنا ننشئ ملف main.cpp ونضع كل الشفرة الإضافية لعرض النافذة هناك:

MAIN.CPP

 #include <SFML/Graphics.hpp> #include <chrono> #include <cstdlib> #include <cmath> //SFML REQUIRED TO LAUNCH THIS CODE #define SCALE 2 #define WINDOW_WIDTH 1280 #define WINDOW_HEIGHT 720 #define FIELD_WIDTH WINDOW_WIDTH / SCALE #define FIELD_HEIGHT WINDOW_HEIGHT / SCALE static struct Config { float velocityDiffusion; float pressure; float vorticity; float colorDiffusion; float densityDiffusion; float forceScale; float bloomIntense; int radius; bool bloomEnabled; } config; void setConfig(float vDiffusion = 0.8f, float pressure = 1.5f, float vorticity = 50.0f, float cDiffuion = 0.8f, float dDiffuion = 1.2f, float force = 1000.0f, float bloomIntense = 25000.0f, int radius = 100, bool bloom = true); void computeField(uint8_t* result, float dt, int x1pos = -1, int y1pos = -1, int x2pos = -1, int y2pos = -1, bool isPressed = false); void cudaInit(size_t xSize, size_t ySize); void cudaExit(); int main() { cudaInit(FIELD_WIDTH, FIELD_HEIGHT); srand(time(NULL)); sf::RenderWindow window(sf::VideoMode(WINDOW_WIDTH, WINDOW_HEIGHT), ""); auto start = std::chrono::system_clock::now(); auto end = std::chrono::system_clock::now(); sf::Texture texture; sf::Sprite sprite; std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); texture.create(FIELD_WIDTH, FIELD_HEIGHT); sf::Vector2i mpos1 = { -1, -1 }, mpos2 = { -1, -1 }; bool isPressed = false; bool isPaused = false; while (window.isOpen()) { end = std::chrono::system_clock::now(); std::chrono::duration<float> diff = end - start; window.setTitle("Fluid simulator " + std::to_string(int(1.0f / diff.count())) + " fps"); start = end; window.clear(sf::Color::White); sf::Event event; while (window.pollEvent(event)) { if (event.type == sf::Event::Closed) window.close(); if (event.type == sf::Event::MouseButtonPressed) { if (event.mouseButton.button == sf::Mouse::Button::Left) { mpos1 = { event.mouseButton.x, event.mouseButton.y }; mpos1 /= SCALE; isPressed = true; } else { isPaused = !isPaused; } } if (event.type == sf::Event::MouseButtonReleased) { isPressed = false; } if (event.type == sf::Event::MouseMoved) { std::swap(mpos1, mpos2); mpos2 = { event.mouseMove.x, event.mouseMove.y }; mpos2 /= SCALE; } } float dt = 0.02f; if (!isPaused) computeField(pixelBuffer.data(), dt, mpos1.x, mpos1.y, mpos2.x, mpos2.y, isPressed); texture.update(pixelBuffer.data()); sprite.setTexture(texture); sprite.setScale({ SCALE, SCALE }); window.draw(sprite); window.display(); } cudaExit(); return 0; }

خط في بداية الوظيفة الرئيسية

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4);

ينشئ صورة RGBA كصفيف أحادي البعد بطول ثابت. سنقوم بتمريرها مع معلمات أخرى (موضع الماوس ، الفرق بين الإطارات) إلى وظيفة computeField . يتم الإعلان عن الأخير ، وكذلك العديد من الوظائف الأخرى ، في kernel.cu واستدعاء الكود الذي تم تنفيذه على وحدة معالجة الرسومات. يمكنك العثور على وثائق على أي من الوظائف على موقع SFML ، ولا يوجد شيء مثير للاهتمام في كود الملف ، لذلك لن نتوقف عند هذا الحد لفترة طويلة.

GPU الحوسبة

لبدء كتابة التعليمات البرمجية تحت gpu ، قم أولاً بإنشاء ملف kernel.cu وحدد العديد من الفئات المساعدة فيه: Color3f و Vec2 و Config و SystemConfig :

kernel.cu (هياكل البيانات)

 struct Vec2 { float x = 0.0, y = 0.0; __device__ Vec2 operator-(Vec2 other) { Vec2 res; res.x = this->x - other.x; res.y = this->y - other.y; return res; } __device__ Vec2 operator+(Vec2 other) { Vec2 res; res.x = this->x + other.x; res.y = this->y + other.y; return res; } __device__ Vec2 operator*(float d) { Vec2 res; res.x = this->x * d; res.y = this->y * d; return res; } }; struct Color3f { float R = 0.0f; float G = 0.0f; float B = 0.0f; __host__ __device__ Color3f operator+ (Color3f other) { Color3f res; res.R = this->R + other.R; res.G = this->G + other.G; res.B = this->B + other.B; return res; } __host__ __device__ Color3f operator* (float d) { Color3f res; res.R = this->R * d; res.G = this->G * d; res.B = this->B * d; return res; } }; struct Particle { Vec2 u; // velocity Color3f color; }; static struct Config { float velocityDiffusion; float pressure; float vorticity; float colorDiffusion; float densityDiffusion; float forceScale; float bloomIntense; int radius; bool bloomEnabled; } config; static struct SystemConfig { int velocityIterations = 20; int pressureIterations = 40; int xThreads = 64; int yThreads = 1; } sConfig; void setConfig( float vDiffusion = 0.8f, float pressure = 1.5f, float vorticity = 50.0f, float cDiffuion = 0.8f, float dDiffuion = 1.2f, float force = 5000.0f, float bloomIntense = 25000.0f, int radius = 500, bool bloom = true ) { config.velocityDiffusion = vDiffusion; config.pressure = pressure; config.vorticity = vorticity; config.colorDiffusion = cDiffuion; config.densityDiffusion = dDiffuion; config.forceScale = force; config.bloomIntense = bloomIntense; config.radius = radius; config.bloomEnabled = bloom; } static const int colorArraySize = 7; Color3f colorArray[colorArraySize]; static Particle* newField; static Particle* oldField; static uint8_t* colorField; static size_t xSize, ySize; static float* pressureOld; static float* pressureNew; static float* vorticityField; static Color3f currentColor; static float elapsedTime = 0.0f; static float timeSincePress = 0.0f; static float bloomIntense; int lastXpos = -1, lastYpos = -1;

السمة __host__ أمام اسم الأسلوب تعني أنه يمكن تنفيذ التعليمات البرمجية على وحدة المعالجة المركزية ، __device__ ، على العكس من ذلك ، يلزم المترجم بجمع الكود تحت GPU. تعلن الكود عن بدائل للعمل مع المتجهات المكونة ، اللون ، التكوينات مع المعلمات التي يمكن تغييرها في وقت التشغيل ، وكذلك العديد من المؤشرات الثابتة للصفائف ، والتي سوف نستخدمها كمخازن للحسابات.

يتم تعريف cudaInit و cudaExit أيضًا بشكل تافه للغاية:

kernel.cu (الحرف الأول)

 void cudaInit(size_t x, size_t y) { setConfig(); colorArray[0] = { 1.0f, 0.0f, 0.0f }; colorArray[1] = { 0.0f, 1.0f, 0.0f }; colorArray[2] = { 1.0f, 0.0f, 1.0f }; colorArray[3] = { 1.0f, 1.0f, 0.0f }; colorArray[4] = { 0.0f, 1.0f, 1.0f }; colorArray[5] = { 1.0f, 0.0f, 1.0f }; colorArray[6] = { 1.0f, 0.5f, 0.3f }; int idx = rand() % colorArraySize; currentColor = colorArray[idx]; xSize = x, ySize = y; cudaSetDevice(0); cudaMalloc(&colorField, xSize * ySize * 4 * sizeof(uint8_t)); cudaMalloc(&oldField, xSize * ySize * sizeof(Particle)); cudaMalloc(&newField, xSize * ySize * sizeof(Particle)); cudaMalloc(&pressureOld, xSize * ySize * sizeof(float)); cudaMalloc(&pressureNew, xSize * ySize * sizeof(float)); cudaMalloc(&vorticityField, xSize * ySize * sizeof(float)); } void cudaExit() { cudaFree(colorField); cudaFree(oldField); cudaFree(newField); cudaFree(pressureOld); cudaFree(pressureNew); cudaFree(vorticityField); }

في وظيفة التهيئة ، نخصص ذاكرة للصفيفات ثنائية الأبعاد ، ونحدد مجموعة من الألوان التي سنستخدمها لطلاء السائل ، وكذلك تعيين القيم الافتراضية في التكوين. في cudaExit ، نقوم فقط بتحرير جميع المخازن المؤقتة. من المفارقات التي تبدو ، لتخزين المصفوفات ثنائية الأبعاد ، من الأفضل استخدام المصفوفات أحادية البعد ، والتي سيتم الوصول إليها بالتعبير التالي:

 array[y * size_x + x]; // equals to array[y][x]

نبدأ في تنفيذ الخوارزمية المباشرة مع وظيفة إزاحة الجسيمات. يتم نقل الحقول oldField و newField (الحقل الذي تأتي منه البيانات ومن أين تتم كتابتها إلى) ، وحجم المصفوفة ، وكذلك دلتا الوقت ومعامل الكثافة (المستخدمة لتسريع إذابة الصبغة في السائل وجعل الوسيط غير حساس للغاية لل advect ، إلى advect إجراءات المستخدم). يتم تنفيذ وظيفة الاستيفاء الثنائية الخطية بطريقة كلاسيكية عن طريق حساب القيم الوسيطة:

kernel.cu (advect)

 // interpolates quantity of grid cells __device__ Particle interpolate(Vec2 v, Particle* field, size_t xSize, size_t ySize) { float x1 = (int)vx; float y1 = (int)vy; float x2 = (int)vx + 1; float y2 = (int)vy + 1; Particle q1, q2, q3, q4; #define CLAMP(val, minv, maxv) min(maxv, max(minv, val)) #define SET(Q, x, y) Q = field[int(CLAMP(y, 0.0f, ySize - 1.0f)) * xSize + int(CLAMP(x, 0.0f, xSize - 1.0f))] SET(q1, x1, y1); SET(q2, x1, y2); SET(q3, x2, y1); SET(q4, x2, y2); #undef SET #undef CLAMP float t1 = (x2 - vx) / (x2 - x1); float t2 = (vx - x1) / (x2 - x1); Vec2 f1 = q1.u * t1 + q3.u * t2; Vec2 f2 = q2.u * t1 + q4.u * t2; Color3f C1 = q2.color * t1 + q4.color * t2; Color3f C2 = q2.color * t1 + q4.color * t2; float t3 = (y2 - vy) / (y2 - y1); float t4 = (vy - y1) / (y2 - y1); Particle res; res.u = f1 * t3 + f2 * t4; res.color = C1 * t3 + C2 * t4; return res; } // adds quantity to particles using bilinear interpolation __global__ void advect(Particle* newField, Particle* oldField, size_t xSize, size_t ySize, float dDiffusion, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float decay = 1.0f / (1.0f + dDiffusion * dt); Vec2 pos = { x * 1.0f, y * 1.0f }; Particle& Pold = oldField[y * xSize + x]; // find new particle tracing where it came from Particle p = interpolate(pos - Pold.u * dt, oldField, xSize, ySize); pu = pu * decay; p.color = p.color * decay; newField[y * xSize + x] = p; }

تقرر تقسيم وظيفة نشر اللزوجة إلى عدة أجزاء: يُسمى computeDiffusion من الكود الرئيسي ، الذي يطلق على diffuse and computeColor عددًا محددًا مسبقًا من المرات ، ثم يستبدل الصفيف من حيث نأخذ البيانات والآخر حيث نكتبها . هذه هي أسهل طريقة لتنفيذ معالجة البيانات الموازية ، لكننا ننفق ضعف الذاكرة.

كلتا الدالتين تسبب اختلافات في طريقة جاكوبي. يتحقق نص jacobiColor و jacobiVelocity على الفور من أن العناصر الحالية ليست على الحدود - في هذه الحالة ، يجب أن نضبطها وفقًا للصيغ الموضحة في قسم الشروط والحدود الأولية .

kernel.cu (منتشر)

 // performs iteration of jacobi method on color grid field __device__ Color3f jacobiColor(Particle* colorField, size_t xSize, size_t ySize, Vec2 pos, Color3f B, float alpha, float beta) { Color3f xU, xD, xL, xR, res; int x = pos.x; int y = pos.y; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = colorField[int(y) * xSize + int(x)] SET(xU, x, y - 1).color; SET(xD, x, y + 1).color; SET(xL, x - 1, y).color; SET(xR, x + 1, y).color; #undef SET res = (xU + xD + xL + xR + B * alpha) * (1.0f / beta); return res; } // calculates color field diffusion __global__ void computeColor(Particle* newField, Particle* oldField, size_t xSize, size_t ySize, float cDiffusion, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Vec2 pos = { x * 1.0f, y * 1.0f }; Color3f c = oldField[y * xSize + x].color; float alpha = cDiffusion * cDiffusion / dt; float beta = 4.0f + alpha; // perfom one iteration of jacobi method (diffuse method should be called 20-50 times per cell) newField[y * xSize + x].color = jacobiColor(oldField, xSize, ySize, pos, c, alpha, beta); } // performs iteration of jacobi method on velocity grid field __device__ Vec2 jacobiVelocity(Particle* field, size_t xSize, size_t ySize, Vec2 v, Vec2 B, float alpha, float beta) { Vec2 vU = B * -1.0f, vD = B * -1.0f, vR = B * -1.0f, vL = B * -1.0f; #define SET(U, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) U = field[int(y) * xSize + int(x)].u SET(vU, vx, vy - 1); SET(vD, vx, vy + 1); SET(vL, vx - 1, vy); SET(vR, vx + 1, vy); #undef SET v = (vU + vD + vL + vR + B * alpha) * (1.0f / beta); return v; } // calculates nonzero divergency velocity field u __global__ void diffuse(Particle* newField, Particle* oldField, size_t xSize, size_t ySize, float vDiffusion, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Vec2 pos = { x * 1.0f, y * 1.0f }; Vec2 u = oldField[y * xSize + x].u; // perfoms one iteration of jacobi method (diffuse method should be called 20-50 times per cell) float alpha = vDiffusion * vDiffusion / dt; float beta = 4.0f + alpha; newField[y * xSize + x].u = jacobiVelocity(oldField, xSize, ySize, pos, u, alpha, beta); } // performs several iterations over velocity and color fields void computeDiffusion(dim3 numBlocks, dim3 threadsPerBlock, float dt) { // diffuse velocity and color for (int i = 0; i < sConfig.velocityIterations; i++) { diffuse<<<numBlocks, threadsPerBlock>>>(newField, oldField, xSize, ySize, config.velocityDiffusion, dt); computeColor<<<numBlocks, threadsPerBlock>>>(newField, oldField, xSize, ySize, config.colorDiffusion, dt); std::swap(newField, oldField); } }

يتم استخدام القوة الخارجية من خلال وظيفة واحدة - applyForce ، والتي تأخذ كحجة موقف الماوس ولون الصبغة ، وكذلك دائرة نصف قطرها العمل. مع ذلك ، يمكننا إعطاء السرعة للجزيئات ، وكذلك طلاء لهم. يتيح لك الأس الشقيق جعل المنطقة غير حادة جدًا ، وفي نفس الوقت واضح تمامًا في نصف القطر المحدد.

kernel.cu (القوة)

 // applies force and add color dye to the particle field __global__ void applyForce(Particle* field, size_t xSize, size_t ySize, Color3f color, Vec2 F, Vec2 pos, int r, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float e = expf((-(powf(x - pos.x, 2) + powf(y - pos.y, 2))) / r); Vec2 uF = F * dt * e; Particle& p = field[y * xSize + x]; pu = pu + uF; color = color * e + p.color; p.color.R = min(1.0f, color.R); p.color.G = min(1.0f, color.G); p.color.B = min(1.0f, color.B); }

إن حساب الدوامة هو بالفعل عملية أكثر تعقيدًا ، وبالتالي ننفذها في حساب vorticity وطبق Vorticity ، نلاحظ أيضًا أنه من الضروري بالنسبة لهما تحديد اثنين من مشغلي الموجات مثل curl (الدوار) و absGradient (تدرج قيم الحقل المطلقة). لتحديد تأثيرات دوامة إضافية ، فإننا نضرب

$ذ$ مكون من ناقلات التدرج على

$-1 دولا$ ، ثم قم بتطبيعه عن طريق القسمة على الطول (دون أن ننسى التحقق من أن الموجه غير صفري):

kernel.cu (دوامة)

 // computes curl of velocity field __device__ float curl(Particle* field, size_t xSize, size_t ySize, int x, int y) { Vec2 C = field[int(y) * xSize + int(x)].u; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] float x1 = -Cx, x2 = -Cx, y1 = -Cy, y2 = -Cy; SET(x1, x + 1, y).ux; SET(x2, x - 1, y).ux; SET(y1, x, y + 1).uy; SET(y2, x, y - 1).uy; #undef SET float res = ((y1 - y2) - (x1 - x2)) * 0.5f; return res; } // computes absolute value gradient of vorticity field __device__ Vec2 absGradient(float* field, size_t xSize, size_t ySize, int x, int y) { float C = field[int(y) * xSize + int(x)]; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] float x1 = C, x2 = C, y1 = C, y2 = C; SET(x1, x + 1, y); SET(x2, x - 1, y); SET(y1, x, y + 1); SET(y2, x, y - 1); #undef SET Vec2 res = { (abs(x1) - abs(x2)) * 0.5f, (abs(y1) - abs(y2)) * 0.5f }; return res; } // computes vorticity field which should be passed to applyVorticity function __global__ void computeVorticity(float* vField, Particle* field, size_t xSize, size_t ySize) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; vField[y * xSize + x] = curl(field, xSize, ySize, x, y); } // applies vorticity to velocity field __global__ void applyVorticity(Particle* newField, Particle* oldField, float* vField, size_t xSize, size_t ySize, float vorticity, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Particle& pOld = oldField[y * xSize + x]; Particle& pNew = newField[y * xSize + x]; Vec2 v = absGradient(vField, xSize, ySize, x, y); vy *= -1.0f; float length = sqrtf(vx * vx + vy * vy) + 1e-5f; Vec2 vNorm = v * (1.0f / length); Vec2 vF = vNorm * vField[y * xSize + x] * vorticity; pNew = pOld; pNew.u = pNew.u + vF * dt; }

ستكون الخطوة التالية في الخوارزمية هي حساب مجال الضغط القياسي وإسقاطه على حقل السرعة. للقيام بذلك ، نحتاج إلى تنفيذ 4 وظائف هي: التباعد ، والذي سينظر في سرعة التباعد ، jacobiPressure ، الذي ينفذ طريقة Jacobi للضغط ، و computePressure باستخدام computePressureImpl ، والذي يكرر حسابات الحقل:

kernel.cu (الضغط)

 // performs iteration of jacobi method on pressure grid field __device__ float jacobiPressure(float* pressureField, size_t xSize, size_t ySize, int x, int y, float B, float alpha, float beta) { float C = pressureField[int(y) * xSize + int(x)]; float xU = C, xD = C, xL = C, xR = C; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = pressureField[int(y) * xSize + int(x)] SET(xU, x, y - 1); SET(xD, x, y + 1); SET(xL, x - 1, y); SET(xR, x + 1, y); #undef SET float pressure = (xU + xD + xL + xR + alpha * B) * (1.0f / beta); return pressure; } // computes divergency of velocity field __device__ float divergency(Particle* field, size_t xSize, size_t ySize, int x, int y) { Particle& C = field[int(y) * xSize + int(x)]; float x1 = -1 * Cux, x2 = -1 * Cux, y1 = -1 * Cuy, y2 = -1 * Cuy; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] SET(x1, x + 1, y).ux; SET(x2, x - 1, y).ux; SET(y1, x, y + 1).uy; SET(y2, x, y - 1).uy; #undef SET return (x1 - x2 + y1 - y2) * 0.5f; } // performs iteration of jacobi method on pressure field __global__ void computePressureImpl(Particle* field, size_t xSize, size_t ySize, float* pNew, float* pOld, float pressure, float dt) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float div = divergency(field, xSize, ySize, x, y); float alpha = -1.0f * pressure * pressure; float beta = 4.0; pNew[y * xSize + x] = jacobiPressure(pOld, xSize, ySize, x, y, div, alpha, beta); } // performs several iterations over pressure field void computePressure(dim3 numBlocks, dim3 threadsPerBlock, float dt) { for (int i = 0; i < sConfig.pressureIterations; i++) { computePressureImpl<<<numBlocks, threadsPerBlock>>>(oldField, xSize, ySize, pressureNew, pressureOld, config.pressure, dt); std::swap(pressureOld, pressureNew); } }

يناسب الإسقاط وظيفتين صغيرتين - المشروع والتدرج الذي يستدعي الضغط. يمكن قول ذلك في المرحلة الأخيرة من خوارزمية المحاكاة لدينا:

kernel.cu (مشروع)

 // computes gradient of pressure field __device__ Vec2 gradient(float* field, size_t xSize, size_t ySize, int x, int y) { float C = field[y * xSize + x]; #define SET(P, x, y) if (x < xSize && x >= 0 && y < ySize && y >= 0) P = field[int(y) * xSize + int(x)] float x1 = C, x2 = C, y1 = C, y2 = C; SET(x1, x + 1, y); SET(x2, x - 1, y); SET(y1, x, y + 1); SET(y2, x, y - 1); #undef SET Vec2 res = { (x1 - x2) * 0.5f, (y1 - y2) * 0.5f }; return res; } // projects pressure field on velocity field __global__ void project(Particle* newField, size_t xSize, size_t ySize, float* pField) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; Vec2& u = newField[y * xSize + x].u; u = u - gradient(pField, xSize, ySize, x, y); }

بعد الإسقاط ، يمكننا المضي قدمًا بأمان في تقديم الصورة إلى المخزن المؤقت والتأثيرات اللاحقة المختلفة. تقوم وظيفة الطلاء بنسخ الألوان من حقل الجسيمات إلى صفيف RGBA. تم أيضًا تطبيق وظيفة ApplyBloom ، والتي تبرز السائل عند وضع المؤشر عليه والضغط على زر الماوس. من التجربة ، تجعل هذه التقنية الصورة أكثر متعة وإثارة للاهتمام لعيون المستخدم ، ولكنها ليست ضرورية على الإطلاق.

في مرحلة ما بعد المعالجة ، يمكنك أيضًا تسليط الضوء على الأماكن التي يكون فيها السائل أعلى سرعة ، وتغيير اللون اعتمادًا على ناقل الحركة ، وإضافة تأثيرات مختلفة ، وما إلى ذلك ، ولكن في حالتنا سنقتصر على نوع من الحد الأدنى ، لأنه حتى الصور رائعة للغاية (خاصة في الديناميات) :

kernel.cu (الطلاء)

 // adds flashlight effect near the mouse position __global__ void applyBloom(uint8_t* colorField, size_t xSize, size_t ySize, int xpos, int ypos, float bloomIntense) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; int pos = 4 * (y * xSize + x); float e = expf(-(powf(x - xpos, 2) + powf(y - ypos, 2)) * (1.0f / (bloomIntense + 1e-5f))); uint8_t R = colorField[pos + 0]; uint8_t G = colorField[pos + 1]; uint8_t B = colorField[pos + 2]; uint8_t maxval = max(R, max(G, B)); colorField[pos + 0] = min(255.0f, R + maxval * e); colorField[pos + 1] = min(255.0f, G + maxval * e); colorField[pos + 2] = min(255.0f, B + maxval * e); } // fills output image with corresponding color __global__ void paint(uint8_t* colorField, Particle* field, size_t xSize, size_t ySize) { int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; float R = field[y * xSize + x].color.R; float G = field[y * xSize + x].color.G; float B = field[y * xSize + x].color.B; colorField[4 * (y * xSize + x) + 0] = min(255.0f, 255.0f * R); colorField[4 * (y * xSize + x) + 1] = min(255.0f, 255.0f * G); colorField[4 * (y * xSize + x) + 2] = min(255.0f, 255.0f * B); colorField[4 * (y * xSize + x) + 3] = 255; }

وفي النهاية ، لا يزال لدينا وظيفة رئيسية واحدة نسميها من main.cpp - computeField . إنه يربط جميع أجزاء الخوارزمية معًا ويدعو الكود الموجود على بطاقة الفيديو ، كما ينسخ البيانات من وحدة المعالجة المركزية إلى وحدة المعالجة المركزية. كما أنه يحتوي على حساب الزخم المتجه واختيار لون الصبغة ، والذي نمرره لتطبيق :

kernel.cu (الوظيفة الرئيسية)

 // main function, calls vorticity -> diffusion -> force -> pressure -> project -> advect -> paint -> bloom void computeField(uint8_t* result, float dt, int x1pos, int y1pos, int x2pos, int y2pos, bool isPressed) { dim3 threadsPerBlock(sConfig.xThreads, sConfig.yThreads); dim3 numBlocks(xSize / threadsPerBlock.x, ySize / threadsPerBlock.y); // curls and vortisity computeVorticity<<<numBlocks, threadsPerBlock>>>(vorticityField, oldField, xSize, ySize); applyVorticity<<<numBlocks, threadsPerBlock>>>(newField, oldField, vorticityField, xSize, ySize, config.vorticity, dt); std::swap(oldField, newField); // diffuse velocity and color computeDiffusion(numBlocks, threadsPerBlock, dt); // apply force if (isPressed) { timeSincePress = 0.0f; elapsedTime += dt; // apply gradient to color int roundT = int(elapsedTime) % colorArraySize; int ceilT = int((elapsedTime) + 1) % colorArraySize; float w = elapsedTime - int(elapsedTime); currentColor = colorArray[roundT] * (1 - w) + colorArray[ceilT] * w; Vec2 F; float scale = config.forceScale; Fx = (x2pos - x1pos) * scale; Fy = (y2pos - y1pos) * scale; Vec2 pos = { x2pos * 1.0f, y2pos * 1.0f }; applyForce<<<numBlocks, threadsPerBlock>>>(oldField, xSize, ySize, currentColor, F, pos, config.radius, dt); } else { timeSincePress += dt; } // compute pressure computePressure(numBlocks, threadsPerBlock, dt); // project project<<<numBlocks, threadsPerBlock>>>(oldField, xSize, ySize, pressureOld); cudaMemset(pressureOld, 0, xSize * ySize * sizeof(float)); // advect advect<<<numBlocks, threadsPerBlock>>>(newField, oldField, xSize, ySize, config.densityDiffusion, dt); std::swap(newField, oldField); // paint image paint<<<numBlocks, threadsPerBlock>>>(colorField, oldField, xSize, ySize); // apply bloom in mouse pos if (config.bloomEnabled && timeSincePress < 5.0f) { applyBloom<<<numBlocks, threadsPerBlock>>>(colorField, xSize, ySize, x2pos, y2pos, config.bloomIntense / timeSincePress); } // copy image to cpu size_t size = xSize * ySize * 4 * sizeof(uint8_t); cudaMemcpy(result, colorField, size, cudaMemcpyDeviceToHost); cudaError_t error = cudaGetLastError(); if (error != cudaSuccess) { std::cout << cudaGetErrorName(error) << std::endl; } }

استنتاج

في هذه المقالة ، قمنا بتحليل خوارزمية رقمية لحل معادلة Navier-Stokes وكتبنا برنامج محاكاة صغير لسائل غير قابل للضغط. ربما لم نفهم جميع التعقيدات ، لكنني آمل أن تكون المادة مثيرة للاهتمام ومفيدة بالنسبة لك ، وكانت بمثابة مقدمة جيدة على الأقل في مجال نمذجة السوائل.

بصفتي مؤلف هذا المقال ، سأقدر بإخلاص أي تعليقات وإضافات ، وسأحاول الإجابة على جميع أسئلتك تحت هذا المنشور.

مواد إضافية

يمكنك العثور على كل شفرة المصدر في هذه المقالة في مستودع جيثب الخاص بي. أي اقتراحات للتحسين هي موضع ترحيب.

المواد الأصلية التي كانت بمثابة أساس لهذه المقالة ، يمكنك أن تقرأ على الموقع الرسمي لنفيديا. كما يقدم أمثلة على تنفيذ أجزاء من الخوارزمية بلغة التظليل:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

يمكن العثور على دليل على نظرية تحلل Helmholtz وكمية هائلة من المواد الإضافية حول ميكانيكا الموائع في هذا الكتاب (الإنجليزية ، انظر القسم 1.2):
Chorin ، AJ ، و JE Marsden. 1993. مقدمة رياضية لميكانيكا الموائع. 3rd ed. الوثاب.

قناة يوتيوب واحدة يتحدث الإنجليزية ، مما يجعل محتوى عالي الجودة يتعلق بالرياضيات ، وحل المعادلات التفاضلية على وجه الخصوص (الإنجليزية). مقاطع الفيديو المرئية للغاية التي تساعد على فهم جوهر العديد من الأشياء في الرياضيات والفيزياء:
3Blue1Brown -
المعادلات التفاضلية في YouTube (3Blue1Brown)

وأشكر أيضًا WhiteBlackGoose على المساعدة في إعداد المواد للمقال.

وفي النهاية ، هناك مكافأة صغيرة - بعض لقطات الشاشة الجميلة التي تم التقاطها في البرنامج: