خوارزمية غروفر والبحث عن البيانات

مرحبا ، habrozhiteli! لقد سلّمنا مؤخرًا كتاب كوان برنارد بعنوان Quantum Computing for Real IT . هنا قرروا مشاركة مقتطف من كتاب "خوارزمية وبيانات البحث في Grover"

نحن ندخل عصر البيانات الكبيرة. يعد البحث عن مجموعات البيانات العملاقة بكفاءة حاليًا مصدر قلق كبير للعديد من الشركات الكبيرة. تعتبر خوارزمية Grover قادرة نظريًا على تسريع عملية استعادة البيانات.

اخترع لوف جروفر خوارزمية له في عام 1996. مثل خوارزميات Deutsch و Simon ، فإن سرعة التنفيذ أعلى مقارنة بالخوارزميات الكلاسيكية من حيث تعقيد الاستعلام. ومع ذلك ، لن نتمكن من تنفيذ خوارزمية استرداد البيانات الحالية دون استخدام أوراكل الذين يمكنهم طرح أسئلتهم. يجب أن نبني خوارزمية تؤدي أعمال أوراكل. ولكن قبل أن نبدأ في الحديث عن تنفيذ خوارزمية Grover ، دعونا نرى ما الذي تقوم به وكيف.

خوارزمية غروفر

تخيل أن لديك أربع أوراق لعب. يتم قلبهم رأسا على عقب. أنت تعرف أن إحداها عبارة عن إيس من الديدان وتحتاج إلى العثور عليها. كم عدد البطاقات التي يجب عليك قلبها حتى تعرف أين تكمن آفة الديدان؟

إذا كنت محظوظًا ، فستجد البطاقة المطلوبة في المحاولة الأولى ، وإذا لم تكن محظوظًا ، فيمكنك قلب ثلاث بطاقات ، ولن يكون أحدها من الدودة. في أسوأ الأحوال ، عند تسليم ثلاث بطاقات ، ستعرف بالتأكيد أن آخر بطاقة هي الدودة التي تبحث عنها. لذلك ، يمكننا معرفة مكان وجود الآس من خلال التقليب من بطاقة إلى ثلاث بطاقات. في المتوسط ​​، تحتاج إلى قلب 2.25 بطاقات.

هذه واحدة من المهام التي تحلها خوارزمية Grover. قبل البدء في وصف الخوارزمية ، نقوم بإعادة صياغة المشكلة. لدينا أربعة تتابعات ثنائية: 00 و 01 و 10 و 11. لدينا دالة و التي تُرجع صفر لثلاثة من هذه التتابعات و 1 للتسلسل الرابع. نحتاج إلى إيجاد التسلسل الثنائي المتوافق مع قيمة الإخراج 1. على سبيل المثال ، يمكننا الحصول على النتائج التالية: f (00) = 0 ، f (01) = 0 ، f (10) = 1 و f (11) = 0. المهمة الآن هي هو معرفة عدد المرات التي يجب حساب الوظيفة من أجل الحصول على النتيجة f (10) = 1. هنا قمنا بإعادة صياغة المشكلة ببساطة عن طريق استبدال أوراق اللعب بالوظائف ، وبالتالي فإن إجابة هذا السؤال معروفة بالفعل: كما كان من قبل ، سيكون من الضروري حساب الوظيفة 2.25 مرات.

كما هو الحال مع جميع خوارزميات استعلام التعقيد ، نقوم ببناء أوراكل - بوابة تغلف وظيفة. أوراكل على سبيل المثال لدينا ، حيث لا يوجد سوى أربعة تسلسلات ثنائية ، هو مبين في الشكل. 9.1.

تظهر سلسلة خوارزمية Grover في الشكل. 9.2.

الخوارزمية ينفذ خطوتين. في البداية ، يتم قلب علامة سعة الاحتمال ، المرتبطة بالمكان الذي نحاول العثور عليه. والثاني يعزز هذا الاحتمال السعة. دعونا نرى كيف تفعل هذه السلسلة.


بعد انتقاله عبر صمامات Hadamard ، يحصل الببتان العلويان على الحالة


و qubit السفلي لديه حالة

الدولة مجتمعة يمكن أن يكتب كما


تمر الكوابيت بعد ذلك عبر البوابة واو. وهي تنقلب 0 و 1 في البوصة الثالثة إلى الموقع الذي نحاول العثور عليه. لحالتنا f (10) = 1 نحصل عليها



يمكن إعادة كتابته كـ



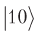
نتيجة لذلك ، نحصل على اثنين من الببتات العليا ، وليس الخلط بينه وبين انخفاض ، ولكن سعة الاحتمال سيغير علامة ، مشيرا إلى الموقع المطلوب.

إذا قمنا بقياس النقطتين العلويتين في هذه الخطوة ، فسنحصل على واحد من أربعة مواقع ، وكل الإجابات الأربعة المحتملة محتملة على حد سواء. نحتاج إلى اتخاذ خطوة أخرى - لزيادة سعة الاحتمال. يتم التضخيم عن طريق عكس تسلسل الأرقام بالنسبة لمتوسطها. إذا كان الرقم أعلى من المتوسط ​​، فإنه ينقلب ويصبح أقل من المتوسط. إذا كان الرقم أقل من المتوسط ​​، فإنه ينقلب ويصبح أعلى من المتوسط. في كل حالة ، يتم الحفاظ على بعد من المتوسط. للتوضيح ، نستخدم أربعة أرقام: 1 و 1 و 1 و -1. مجموعهم 2 ، والمعدل هو 2/4 ، أو 1/2. ثم نبدأ في فرز الأرقام بالتسلسل. الرقم الأول هو 1. وهو 1/2 أعلى من المتوسط. بعد الانقلاب ، يجب أن يكون 1/2 أقل من المتوسط. في هذه الحالة ، سيتحول إلى 0. الرقم -1 أقل من المتوسط ​​بمقدار 3/2. بعد الانقلاب ، يجب أن يصبح 3/2 أعلى من المتوسط ​​، أي يتحول إلى 2.

اثنين من qubits العليا لديها حاليا حالة


تحويل السعات نسبة إلى المتوسط ​​، نحصل عليه .
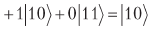
بعد الانتهاء من القياس ، سنحصل بالتأكيد على 10 ، أي أن الثورة بالنسبة إلى المتوسط ​​تمنحنا بالضبط ما نحتاج إليه. كل ما يتعين علينا القيام به هو التأكد من وجود بوابة ، أو ما هو الشيء نفسه ، مصفوفة متعامدة تصف الثورة بالنسبة إلى المتوسط. هذه المصفوفة موجودة:


كنتيجة لعمل الصمام الموجود في العلمين العلويين


في هذا المثال ، حيث يوجد لدينا اثنين فقط من البتات ، يجب علينا استخدام أوراكل مرة واحدة فقط. يكفي أن نطرح السؤال الوحيد. بالنسبة للحالة n = 2 ، تقدم خوارزمية Grover إجابة دقيقة بعد سؤال واحد ، بينما في الحالة الكلاسيكية ، في المتوسط ​​، يجب طرح 2.25 سؤالًا.

تمتد هذه الفكرة لتشمل عددًا تعسفيًا من n qubits. نبدأ بتحويل علامة السعة الاحتمالية ، والتي تتوافق مع الموقع المطلوب. ثم نقوم بتنفيذ ثورة نسبة إلى المتوسط. ومع ذلك ، في هذه الحالة ، لا يحدث تضخيم السعة بنفس القدر الذي يحدث في الحالة مع اثنين من البتات. خذ على سبيل المثال ثمانية أرقام ، سبعة منها واحدة ورقم واحد -1. مجموعهم هو 6 ، والمعدل هو 6/8. بعد الانقلاب ، يتحول المتوسط ​​1 إلى نصف ، و -1 سوف يتحول إلى 10/4. نتيجة لذلك ، في وجود ثلاث وحدات بت ، وقياس البايت واحد بعد تضخيم السعة ، سوف نحصل على الموقع المطلوب باحتمال أعلى من الآخرين. المشكلة هي أن هناك فرصة كبيرة للحصول على إجابة خاطئة. نحتاج إلى احتمال أكبر للحصول على الإجابة الصحيحة - نحتاج إلى زيادة السعة قبل القياس. الحل هو نقل كل الكيبيتات مرة أخرى من خلال السلسلة. نقلب مرة أخرى علامة السعة الاحتمالية المرتبطة بالموقع المطلوب ونقلب مرة أخرى بالنسبة إلى المتوسط.

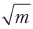
النظر في القضية المعممة. نحن بحاجة إلى إيجاد شيء في أحد المواقع المحتملة. للعثور عليه بالطريقة الكلاسيكية ، في أسوأ الحالات ، يتعين علينا طرح أسئلة m - 1. عدد الأسئلة ينمو في نسبة إلى م. قام Grover بحساب صيغة تحدد عدد المرات التي تحتاج فيها السلسلة إلى الحصول على أقصى احتمال للإجابة الصحيحة. ينمو الرقم الذي تعطيه هذه الصيغة بشكل متناسب . هذا هو تسارع من الدرجة الثانية.

تطبيقات خوارزمية غروفر

هناك العديد من المشاكل في تنفيذ الخوارزمية. أولاً ، يتم تقييم التسارع التربيعي بالنسبة لطلب التعقيد. لاستخدام أوراكل ، ستحتاج إلى إنشائه ، وإذا لم تأخذ هذه المهمة بعناية فائقة ، فإن عدد الخطوات التي تقوم بها أوراكل سوف يفوق عدد الخطوات التي تحفظها الخوارزمية ، ونتيجة لذلك ، ستصبح الخوارزمية أبطأ من السرعة التقليدية. مشكلة أخرى هي أنه من خلال تحديد التسارع ، نفترض أن مجموعة البيانات مضطربة. إذا كانت مجموعة البيانات تحتوي على بنية محددة ، فيمكنك غالبًا العثور على خوارزمية كلاسيكية تستخدم هذه البنية وتبحث عن حل أسرع بكثير. المشكلة الأخيرة مرتبطة بالتسارع. التسارع التربيعي ليس أكثر من تسارع الأسي ، وهو ما لاحظناه في خوارزميات أخرى. هل من الممكن تحقيق المزيد؟ لنلقِ نظرة على هذه القضايا.

كل من المشاكل المرتبطة بتنفيذ أوراكل ووجود هيكل في مجموعة البيانات لها ما يبررها وتبين أنه في معظم الحالات خوارزمية غروفر ليس لها تطبيق عملي للبحث في قاعدة البيانات. ولكن في بعض الحالات ، فإن وجود بنية في البيانات يجعل من الممكن إنشاء أوراكل يعمل بكفاءة عالية. في مثل هذه الحالات ، يمكن للخوارزمية تجاوز الخوارزميات الكلاسيكية. الإجابة على سؤال إمكانية تحقيق نجاح أكبر قد تم تقديمها بالفعل. ثبت أن خوارزمية غروفر هي الأمثل. لا توجد خوارزمية كمية قادرة على حل مشكلة بأكثر من التسارع التربيعي. لا يزال التسارع التربيعي ، رغم أنه غير مثير للإعجاب مثل الأسي ، يوفر بعض الفوائد. عند العمل مع مجموعات البيانات الكبيرة ، يمكن أن يكون أي تسريع قيمة.

من المحتمل أن تجد خوارزمية Grover التطبيق الرئيسي ليس للبحث ، كما تم تقديمه أعلاه ، ولكن بسبب أشكاله. على وجه الخصوص ، قد تكون فكرة تضخيم السعة مفيدة.

لقد درسنا بعض الخوارزميات فقط ، لكن خوارزميات Shore و Grover تعتبر الأكثر أهمية. هناك العديد من الخوارزميات الأخرى استنادًا إلى الأفكار الكامنة في هذين الخيارين. والآن ، دعونا نحول انتباهنا من الخوارزميات الكمية إلى مجالات أخرى لتطبيق الحوسبة الكمومية.