الممارسات الوظيفية والواجهة الأمامية: الموندات والمجانين

مرحبا بالجميع! اسمي ديمتري رودنيف ، أنا مطور الواجهة الأمامية في BCS. لقد بدأت رحلتي بتخطيط واجهات متفاوتة التعقيد ودائماً ما أوليت اهتمامًا خاصًا للواجهة: كم سيكون مريحًا للمستخدم للتفاعل معه ، إذا تمكنت من توصيل المستخدم بالواجهة التي صممها المصمم.



في هذه السلسلة من المقالات التي أود أن أشاركها تجربتي في تطبيق الممارسات الوظيفية في تطوير الواجهة الأمامية ، سأتحدث عن إيجابيات وسلبيات ستحصل عليها كمطور باستخدام هذه الممارسات. إذا كنت تحب الموضوع ، فسوف نغرق في الزوايا "الأكثر جفافًا" والأكثر تعقيدًا في العالم الوظيفي. لاحظت على الفور أننا سننتقل من الأكبر إلى الأصغر ، أي أننا سننظر في التطبيق الكلاسيكي من وجهة نظر عين الطير ، وبينما ننتقل إلى المقالات ، سنذهب إلى حيث تجلب لنا ممارسة محددة فوائد ملحوظة.

لذلك ، لنبدأ بمعالجة الولايات. في نفس الوقت ، سوف أخبرك ، وهنا بشكل عام ، الأحاديات والمجانين.

مقدمة

عند الكشف عن الواجهة التالية وإيجاد أرضية مشتركة بين واجهة المستخدم والتحليلات ، بدأت ألاحظ أنه في كل مرة يتعامل فيها مطور مع شبكة ما ، كان يحتاج فقط إلى معالجة جميع حالات واجهة المستخدم ووصف رد الفعل على حالة معينة. ونظرًا لأن كل واحد منا يسعى إلى التميز ، فهناك رغبة في هذه الطريقة في معالجة الحالات لإظهار نمط يصف بشفافية قدر الإمكان ما يحدث وما هو بادئ رد فعل معين ، ونتيجة لذلك ، نتيجة العمل. لحسن الحظ ، في عالم البرمجة ، تم تنفيذ أي شيء تقريبًا تقريبًا بواسطة شخص ما قبلك.

في كل من عالم التطوير وعالم التصميم ، لم يتم تشكيل الأنماط التي تسمح لك بحل مشاكلك بفعالية ، بل وأيضًا المضادات التي يجب تجنبها بكل الوسائل حتى لا تزدهر الممارسة السيئة ، وكان للمطور أو المصمم دائمًا نقطة ارتكاز في المواقف ، عندما لا يكون هناك حل ملموس.

في حالتنا ، فإن الموقف الذي يواجهه معظم المطورين هو معالجة جميع حالات عنصر واجهة المستخدم ورد الفعل عليها. المشكلة هنا هي أن عنصر واجهة المستخدم يمكن أن يتفاعل مع كل من الحالة المحلية (دون تنفيذ طلبات غير متزامنة) ومع الموارد البعيدة أو المستودعات. ينسى المطورون أحيانًا التعامل مع جميع حالات الحافة ، مما يؤدي إلى سلوك غير متناسق للنظام ككل.

ستحتوي جميع الأمثلة على أمثلة التعليمات البرمجية باستخدام مكتبة React ومجموعة شاملة من JavaScript - TypeScript ، بالإضافة إلى مكتبات البرمجة الوظيفية fp-ts.

النظر في أبسط مثال ، حيث لدينا قائمة من العناصر التي نطلبها من الخادم ، ونحن بحاجة إلى عرض واجهة المستخدم بشكل صحيح وفقا لنتائج الطلب. نحن مهتمون بوظيفة render ، لأننا في حاجة إلى عرض الحالة الصحيحة أثناء تنفيذ الطلب. يمكن الاطلاع على رمز المثال الكامل على العنوان التالي: application simple . في المستقبل ، سيكون هناك مشروع كامل متاح ، يركز على سلسلة من المقالات ، حيث سنقوم خلال الدورة بتفكيك أجزائه الفردية.

  const renderInitial = (...) => ...; const renderPending = (...) => ...; const renderError = (...) => ... ; const renderSuccess = (...) => ... ; return ( {state.subcribers.foldL( renderInitial, renderPending, renderError, renderSuccess, )} ); 

يوضح المثال بوضوح أن كل حالة من حالات نموذج البيانات لها وظيفتها الخاصة ، وأن كل دالة تقوم بإرجاع جزء من واجهة المستخدم الموصوفة لها (رسالة ، زر ، إلخ). التطلع إلى الأمام ، سأقول أن المثال يستخدم RemoteData monad .

هذا أنيق للغاية ، والأهم من ذلك أنه آمن ، يمكننا العمل مع البيانات والرد عليها. كانت هذه مقدمة ، حيث حاولت أن أثبت فوائد النهج الوظيفي في مثال بسيط على ما يبدو.

Functor و Monad

الآن ، لنبدأ في الغوص تدريجياً في نظرية الفئات المطبقة وتحليل مفاهيم مثل Functor و Functor ، وكذلك النظر في ممارسات العمل مع البيانات بأمان باستخدام الممارسات الوظيفية.

"أساسًا ، لا يعد المشغّل أكثر من بنية بيانات تسمح لك بتطبيق وظائف التحويل لاستخراج القيم من الصدفة ، وتعديلها ، ثم إعادتها إلى الغلاف.

يعد تضمين القيم في وعاء أو حاوية نمطًا أساسيًا للتصميم في البرمجة الوظيفية ، لأنه يحمي من الوصول المباشر إلى القيم ، مما يسمح بمعالجتها بأمان ودون تغيير في برامج التطبيقات. "

أخذت هذا الاقتباس من كتاب رائع عن مراجعة تقنيات البرمجة الوظيفية في JavaScript . لنبدأ بالمكون النظري ونحلل ما هو العامل الفعلي. بادئ ذي بدء ، نحن بحاجة إلى التعرف على قسم رائع من الرياضيات يسمى نظرية الفئة على المستوى الأساسي.

نظرية الفئة هي فرع من فروع الرياضيات يدرس خصائص العلاقات بين الأشياء الرياضية ، بغض النظر عن التركيب الداخلي للأشياء. تحتل نظرية الفئة مكانة مركزية في الرياضيات الحديثة ؛ وقد وجدت أيضًا تطبيقات في علوم الكمبيوتر والمنطق والفيزياء النظرية.

تتكون الفئة من كائنات وسهام موجهة بينهما. أسهل طريقة لتصور فئة هي:

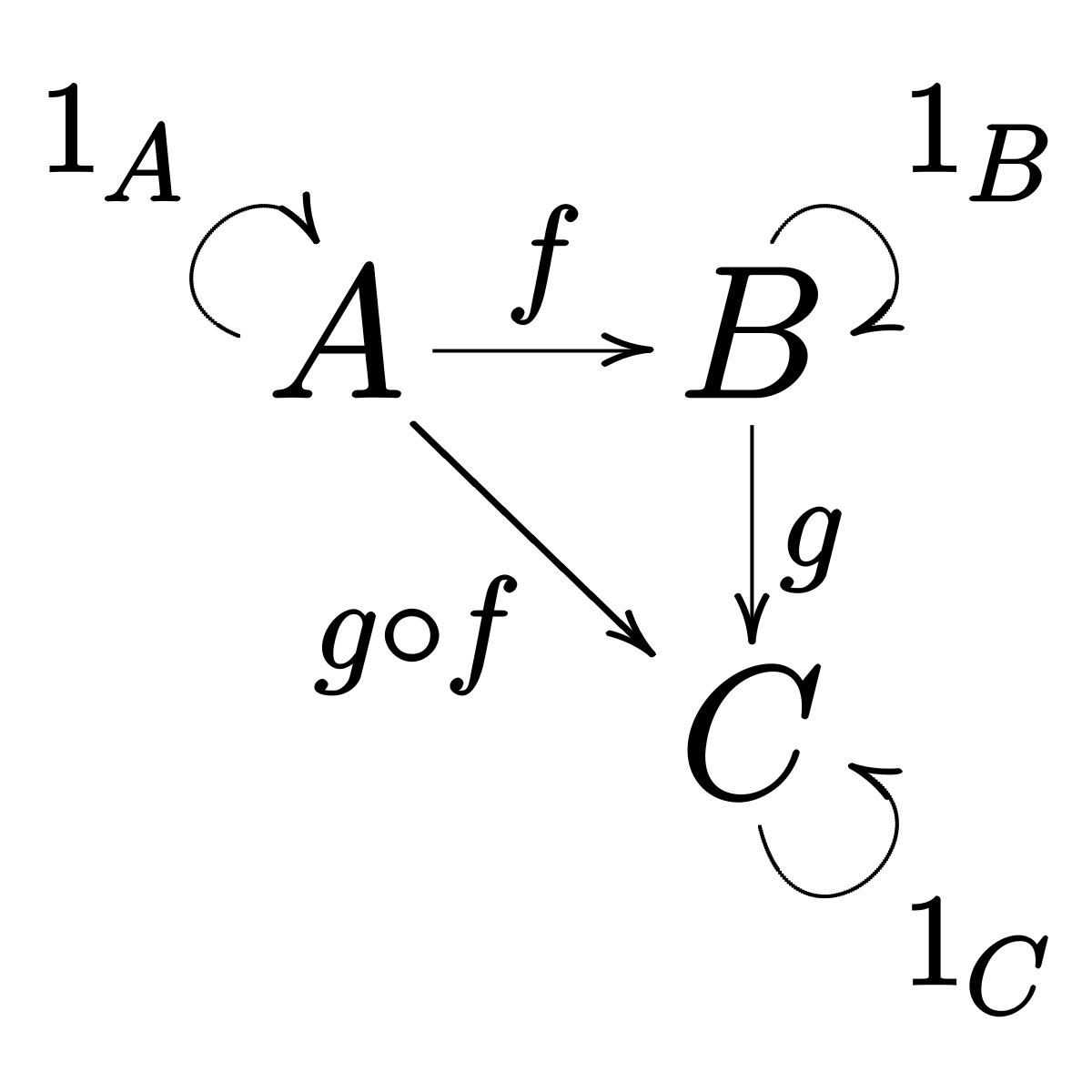
يتم ترتيب الأسهم بحيث إذا كان لديك سهم من كائن A إلى كائن B وسهم من الكائن B إلى C ، فيجب أن يكون هناك سهم - تكوينها من A إلى C. فكر في الأسهم كوظائف ؛ وتسمى أيضا التشكل. لديك دالة f تأخذ A كوسيطة وتعود إلى B. توجد وظيفة أخرى g تأخذ B كوسيطة وتعود إلى C. يمكنك دمجها بتمرير النتيجة من f إلى g . لقد وصفنا للتو وظيفة جديدة تأخذ A وتُرجع C. في الرياضيات ، يُشار إلى مثل هذا التكوين بدائرة صغيرة بين تدوين الوظيفة: g ◦ f. انتبه لترتيب التكوين - من اليمين إلى اليسار.

في الرياضيات ، يتم توجيه التكوين من اليمين إلى اليسار. في هذه الحالة ، يساعدك إذا قرأت g ◦ f كـ "g after f".

 -—   A  B f :: A -> B -—   B   g :: B -> C -— A  C g . f 

هناك نوعان من الخصائص الهامة للغاية التي يجب أن تفيها التركيبة في أي فئة.

1. التراكيب هي ترابطية (associativity هي خاصية للعمليات تسمح لك باستعادة تسلسل تنفيذها في حالة عدم وجود مؤشرات صريحة للخلافة مع أولوية متساوية ؛ وهذا يميز بين associativity اليسرى ، حيث يتم تقييم التعبير من اليسار إلى اليمين ، والجمعيات اليمنى من اليمين إلى اليسار. إذا كان لديك ثلاثة أشكال (سهام) و f و g و h ، والتي يمكن ترتيبها (أي ، أنواعها متوافقة مع بعضها البعض) ، فأنت يحتاج الأقواس لمجموعة منهم. رياضيا، وهذا كما هو مكتوب h ◦ (g ◦ f) = (h ◦ g) ◦ f = h ◦ g ◦ f (ح ◦ ز) ◦ و = ح ز ◦ ◦ و
2. لكل كائن A هناك سهم ، والذي سيكون وحدة التكوين. هذا السهم من كائن إلى نفسه. أن تكون وحدة تكوين تعني أنه عند تكوين وحدة بأي سهم يبدأ على A أو ينتهي على A ، على التوالي ، تُرجع التركيبة السهم نفسه. ويسمى سهم الوحدة للكائن A IDa (الوحدة الموجودة على A). في التدوين الرياضي ، إذا f ◦ idA = f من A إلى B ، ثم f ◦ idA = f
   
   للعمل مع الوظائف ، يتم تطبيق سهم واحد كدالة متطابقة ، والتي تقوم ببساطة بإرجاع الوسيطة الخاصة بها.

الآن يمكننا النظر في ما functor هو في نظرية الفئة.

functor هو نوع خاص من التعيين بين الفئات. يمكن فهمه على أنه شاشة تحافظ على الهيكل. الدالات بين الفئات الصغيرة هي أشكال في فئة الفئات الصغيرة. مجمل جميع الفئات ليست فئة بالمعنى المعتاد ، حيث أن مجمل كائناتها ليست فئة. - ويكيبيديا .

ضع في اعتبارك مثالاً على تنفيذ ل functor للحاوية ربما ، وهي فكرة "القيمة التي قد تكون مفقودة".

 const compose = <A, B, C>( f: (a: A) => B, g: (b: B) => C, ): (a: A) => C => (a: A) => g(f(a)); //  Maybe: type Nothing = Readonly<{ tag: 'Nothing' }>; type Just<A> = Readonly<{ tag: 'Just'; value: A }>; export type Maybe<A> = Nothing | Just<A>; const nothing: Nothing = { tag: 'Nothing' }; const just = <A>(value: A): Just<A> => ({ tag: 'Just', value }); //    Maybe: const fmap = <A, B>(f: (a: A) => B) => (fa: Maybe<A>): Maybe<B> => { switch (fa.tag) { case 'Nothing': return nothing; case 'Just': return just(f(fa.value)); } }; //  1: fmap id === id namespace Laws { console.log( fmap(id)(just(42)), id(just(42)), ); // => { tag: 'Just', value: 42 } //  2: fmap f ◦ fmap g === fmap (f ◦ g) const f = (a: number): string => `Got ${a}!`; const g = (s: string): number => s.length; console.log( compose(fmap(f), fmap(g))(just(42)), fmap(compose(f, g))(just(42)), ); // => { tag: 'Just', value: 7 } } 

يمكن الاطلاع على طريقة fmap من الجانبين:

1. كوسيلة لتطبيق وظيفة خالصة على قيمة "حاوية" ؛
2. كوسيلة ل "رفع في سياق الحاوية" وظيفة نقية.

في الواقع ، إذا كانت الأقواس في الواجهة مختلفة قليلاً ، فيمكننا الحصول على توقيع وظيفة fmap :

 const fmap: <A, B>(f: (a: A) => B) => ((ma: Maybe<A>) => Maybe<B>); 

بعد تعريف الواجهة:

 type Function1<Domain, Codomain> = (a: Domain) => Codomain; 

نحصل على تعريف fmap :

 const fmap: <A, B>(f: (a: A) => B) => Function1<Maybe<A>, Maybe<B>>; 

تتيح لنا هذه الحيلة البسيطة التفكير في المُدرب كطريقة "لرفع وظيفة خالصة في سياق الحاوية". بفضل هذا ، من الممكن التعامل مع أنواع مختلفة من البيانات بطريقة آمنة: على سبيل المثال ، معالجة سلاسل القيم المتداخلة الاختيارية بنجاح ؛ تحويل قوائم البيانات التعامل مع الاستثناءات وأكثر من ذلك.

كما هو موضح سابقًا ، باستخدام عوامل التوجيه ، يمكنك تطبيق الوظائف على القيم بأمان ودون تغيير. تشبه Monads functor ، إلا أنها قادرة على تفويض منطق خاص في حالات خاصة. المشرف نفسه يعرف فقط كيفية تطبيق هذه الوظيفة ولف النتيجة مرة أخرى في قشرة ، وليس لديه منطق إضافي.

ينشأ عنصر أحادي عند إنشاء نوع بيانات كامل بواسطة مبدأ استخراج البيانات عن طريق مبدأ استخراج القيم من الأصداف وتحديد القواعد من التداخل. مثل الدالات ، تعد monads قالب تصميم يستخدم لوصف العمليات الحسابية في شكل سلسلة من المراحل حيث تكون القيمة المعالجة غير معروفة على الإطلاق ، ولكن monads هي التي تجعل من الممكن بأمان وبدون آثار جانبية تتحكم في تدفق البيانات عند استخدامها في التكوين. Monads يمكن أن تهدف إلى حل مجموعة متنوعة من المشاكل. نظريًا ، تعتمد monads على نظام الكتابة بلغة معينة. في الواقع ، يعتقد الكثير من الناس أنه لا يمكن فهمهم إلا في حالة وجود أنواع بيانات واضحة.

من أجل فهم الأحاديات بشكل أفضل ، يجب تعلم المفاهيم المهمة التالية.

الكائن الدقيق الاحادي الخلية. يوفر واجهة مجردة لعمليات monadic
نوع monadic. تنفيذ محدد لهذه الواجهة

لكن أمثلة عملية لتطبيق هذه الخصائص لعامل البناء والإنشاءات الفئوية الأخرى التي سأعرضها في المقالات المستقبلية.