حول إحداثيات مركزية على الأصابع

مرحبا.

من المؤكد أن الجميع قد شهد تقييم ثقب الباب لدرجة تشابه الطفل مع الوالدين: شيء مثل "أبي سكب ، لكنه يشبه أمي أيضًا !!!"


( مأخوذة من هنا )

كما في المثال في الصورة ، يمكنك تقييم درجة التشابه في المئة. يمكنك أيضًا استخدام الأقارب لوصف وجه الطفل بشكل أكثر دقة في شكل مبلغ مرجح لأقارب الأقارب ...

وسوف ينظر وسيُنظر إليه بشكل طبيعي تمامًا لشخص "عادي" لا يرتبط بعلم الإنسان ، أو ، على سبيل المثال ، علم الطب الشرعي. بالنسبة للمحترفين في مجال التحليل والتعرف على الوجوه ، من المرجح أن يكون الوجه الإنساني عبارة عن مجموعة من المعلمات. وهذا هو ، نقطة (مجموعة من الإحداثيات) في بعض الفضاء مع أساس (محاور المقابلة للمعلمات). وإذا وصفنا وجه الطفل مقارنة بأقاربه ، فمن المرجح أن تظهر النقطة المقابلة لوجه الطفل في هذه المساحة من المعلمات داخل بدن محدب من سحابة النقاط المقابلة لوجوه أقرب الأقرباء (ولكن هذا ليس دقيقًا).

في الواقع ، ما أنا عليه ... هذان الطريقان لوصف الوجوه يتوافقان مع نظامين للإحداثيات:

1. متحدة المركز ، وصف لنقطة في الفضاء (في مثالنا: الوجه) من خلال مزيج مرجح من النقاط الأخرى ؛
2. أفيني ، وصف لنقطة في الفضاء من خلال الإحداثيات في بعض الأساس.

فما هي الإحداثيات ثنائية المركز؟

اسمحوا في الفضاء الأبعاد المعطاة نقطة مع ناقلات نصف قطرها . . علاوة على ذلك ، لا تكمن أي من النقاط في القشرة الخطية لمتجهات نصف القطر الخاصة بالنقاط المتبقية ... ببساطة ، إنها بسيطة للغاية: دع هذه النقاط تشكل شخصية لا يمكن تمثيلها بالكامل في مساحة ذات بُعد أقل من .

في حالة الفضاء أحادي البعد (خط) ، نحتاج إلى نقطتين غير متطابقتين ، في حالة الفضاء ثنائي الأبعاد - مثلث غير متحلل ، في حالة ثلاثي الأبعاد - رباعي الأسطح.

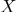
ثم أي نقطة في الفضاء يمكن أن يمثله ناقلات نصف قطرها :



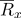
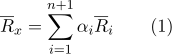
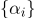
مجموعة وهناك إحداثيات مركزية.

كيف يتم إحداثيات مركزية أفضل / أسوأ من أفيني؟

لنبدأ بالعيوب النسبية:

1. في التمثيل الحركي المركزي ، نحتاج إلى تنسيق واحد أكثر من التمثيل الأقارب ؛
2. لا يمكن حساب المسافة بين النقاط المحددة ثنائية المركز بشكل مباشر في هذه الإحداثيات.

في جزء منه ، يتم تعويض العيب الأول من حقيقة أنه على الرغم من الحاجة إلى استخدام إحداثيات مركزية عند وصف نقطة في مساحة الأبعاد ، لا يزيد عدد الدرجات. ترتبط إحداثيات مركزية المحددة في الصيغة (1) بالعلاقة:



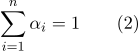
بالنسبة للعيوب الثانية ، إذا كانت هناك حاجة لحساب المسافة بين النقاط الممثلة ثنائية المركز ، فمن المنطقي حساب المنتجات العددية واستخدام التناظرية المسافة Mahalanobis.

ما هي المكافآت من استخدام إحداثيات مركزية؟

1. إحداثيات مركزية هي ثابتة لتحويل تحولات الفضاء. يتم استخدام هذه الخاصية ، على سبيل المثال ، للاستيفاء الخطي في رسومات الكمبيوتر. اسمح لإحداثيات الملمس أن تحدد في رؤوس عنصر السطح الثلاثي 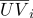والقواعد الطبيعية ( 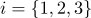) ، ثم كل نقطة من هذا القسم السطحي سيكون لها إحداثيات متحدة المركز 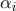إحداثيات الملمس 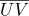وعادي 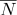يمكن حسابها على النحو التالي:
   
   
   
   
   
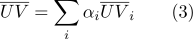
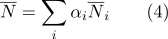
2. من خلال إحداثيات مركزية ، من السهل تحديد ما إذا كانت النقطة تنتمي أم لا 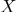أجزاء من الفضاء يحدها متعدد السطوح مع القمم : يتم ذلك فقط إذا . مساواة إحداثية مركزية رقم 1 تعني أن هذه النقطة يتزامن مع . إذا كانت عدة إحداثيات متحدة المركز تساوي 0 ، فهذا يعني أن النقطة تنتمي إلى فضاء فرعي يمتد بواسطة متجهات نصف القطر للنقاط المتبقية التي تزيد إحداثياتها المقابلة عن 0.

ربما يكون من الصعب للغاية حساب؟

لا أكثر تعقيدًا من أي تحول خطي لنظام الإحداثيات. لأنه ، في جوهرها ، حساب إحداثيات مركزية مثل هذا التحول.

نعيد كتابة متجه نصف القطر للنقاط بالشكل التالي:

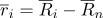
حيث - متجه شعاعي في نظام الإحداثيات المتمركز عند نقطة معينة .

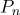
ثم يمكن إعادة كتابة الصيغة (1) بالصيغة التالية:



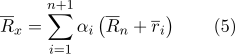
سنكشف عن الأقواس في المجموع:



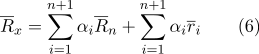
حسب العقار (2):



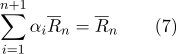
وفقا لذلك:

.

حيث

بالنظر إلى (2) ، فإننا نقتصر على حساب الإحداثيات الأولى ثنائية المركز. تخيل الانتقال إلى إحداثيات مركزية كتحول خطي:

.

حيث - المتجه n للإحداثيات ثنائية المركز (باستثناء الأخير) ، - مصفوفة التحول.

بالنظر إلى خصائص التمثيل الحركي المركزي ، إذا كان استبدال واحد من ناقلات ( ) ، ثم نحصل على متجه بمكونات صفرية ، باستثناء واحد من واحد ، والذي سيكون مساويًا 1.

إذا المصفوفة ضرب المصفوفة تتكون من أعمدة من ، ثم يجب أن نحصل على مصفوفة الهوية (مصفوفة تحتوي على المصفوفة الرئيسية والأصفار في العناصر المتبقية):

.

حيث . هي مصفوفة الهوية ( - رمز كرونكر: 1 إذا خلاف 0).

من (10) نجد :



وبالتالي ، وجود مجموعة من النقاط مع ناقلات نصف قطرها . يمكننا حساب المصفوفة لتحويلها إلى إحداثيات ثنائية المركز:



باستخدام هذه المصفوفة ، يمكننا الحصول على الأول إحداثيات نقطة مركزية مع ناقلات نصف قطرها :



باستخدام العلاقة (2) مرة أخرى ، نحصل على آخر إحداثية متحدة المركز:

استنتاج

ربما للوهلة الأولى ، يبدو أن اللامركزية محرج ومعقد. ولكن في الواقع ، هذه أداة مريحة للغاية ولا غنى عنها في العديد من المهام ، والتي تعتاد عليها بسرعة كبيرة. لأنه لا يوجد سحر هنا ، فهو جبر خطي في أنقى صوره!