الانحدار الخطي ونزول التدرج

دع مؤشرات X و Y ، التي لها تعبير كمي ، تتم دراستها في مجال موضوع معين.

علاوة على ذلك ، هناك كل الأسباب للاعتقاد بأن المؤشر Y يعتمد على المؤشر X. قد يكون هذا الموقف بمثابة فرضية علمية ويستند إلى الحس السليم الأساسي. على سبيل المثال ، خذ محلات البقالة.

تدل بواسطة:

X - منطقة المبيعات (متر مربع. م)

Y - المبيعات السنوية (مليون ع.)

من الواضح أنه كلما ارتفعت مساحة التداول ، زادت قيمة التداول السنوي (نفترض وجود علاقة خطية).

تخيل أن لدينا بيانات عن بعض متاجر n (مساحة البيع بالتجزئة والدوران السنوي) - لدينا مجموعة بيانات ومساحة البيع بالتجزئة k (X) ، والتي نريد أن نتوقع مبيعاتها السنوية (Y) هي مهمتنا.

نفترض أن قيمة Y الخاصة بنا تعتمد على X في النموذج: Y = a + b * X

لحل مشكلتنا ، يجب أن نختار المعاملتين a و b.

أولاً ، دعونا نضع القيم العشوائية a و b. بعد ذلك ، نحتاج إلى تحديد وظيفة الخسارة وخوارزمية التحسين.

للقيام بذلك ، يمكننا استخدام وظيفة الجذر التربيعي لفقدان المربع ( MSELoss ). يتم حسابها بواسطة الصيغة:



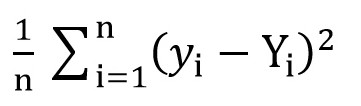
حيث y [i] = a + b * x [i] بعد a = rand () و b = rand () ، و Y [i] هي القيمة الصحيحة لـ x [i].
في هذه المرحلة ، لدينا الانحراف المعياري (دالة معينة لـ a و b). ومن الواضح أنه كلما كانت قيمة هذه الوظيفة أصغر ، كلما تم تحديد المعلمتين (أ) و (ب) بشكل أكثر دقة فيما يتعلق بتلك المعلمات التي تصف العلاقة الدقيقة بين مساحة مساحة البيع والدوران في هذه الغرفة.

الآن يمكننا البدء في استخدام النسب المتدرج (فقط لتقليل وظيفة الخسارة).

نزول التدرج

جوهرها بسيط جدا. على سبيل المثال ، لدينا وظيفة:

y = x*x + 4 * x + 3 

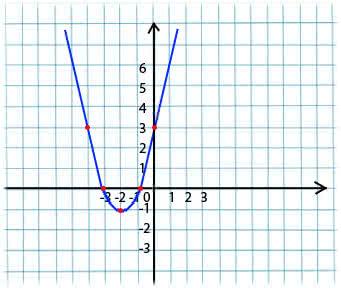
نأخذ قيمة تعسفية لـ x من مجال تعريف الوظيفة. تخيل أن هذه هي النقطة x1 = -4.

بعد ذلك ، نأخذ المشتق فيما يتعلق x لهذه الدالة في النقطة x1 (إذا كانت الوظيفة تعتمد على عدة متغيرات (على سبيل المثال ، a و b) ، فإننا نحتاج إلى أخذ المشتقات الجزئية لكل من المتغيرات). y '(x1) = -4 <0

الآن نحصل على قيمة جديدة لـ x: x2 = x1 - lr * y '(x1). تتيح لك المعلمة lr (معدل التعلم) ضبط حجم الخطوة. وبالتالي نحصل على:

إذا كان المشتق الجزئي عند نقطة معينة x1 <0 (تنقص الوظيفة) ، فإننا ننتقل إلى نقطة الحد الأدنى المحلي. (x2 سيكون أكبر من x1)

إذا كان المشتق الجزئي عند نقطة معينة x1> 0 (تزيد الدالة) ، فإننا لا نزال ننتقل إلى نقطة الحد الأدنى المحلي. (x2 سيكون أقل من x1)

من خلال إجراء هذه الخوارزمية بشكل متكرر ، سنقترب من الحد الأدنى (ولكن لن نصل إليه).

في الممارسة العملية ، يبدو كل هذا أبسط بكثير (ومع ذلك ، لا أفترض أن أقول أي من المعاملين a و b سوف يتناسبان مع الحالة المذكورة أعلاه بدقة أكبر مع المحلات التجارية ، لذلك نأخذ الاعتماد على النموذج y = 1 + 2 * x لإنشاء مجموعة البيانات ، ثم تدريب نموذجنا على مجموعة البيانات هذه):
(الرمز مكتوب هنا )

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

بعد تجميع الشفرة ، يمكنك أن ترى أن القيم الأولية لـ a و b كانت بعيدة عن المطلوبين 1 و 2 ، على التوالي ، والقيم النهائية قريبة جدًا.

سأوضح قليلاً عن سبب اعتبار a_grad و b_grad بهذه الطريقة.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) . سيكون مشتق جزئي لـ F فيما يتعلق بإرادة -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error . سيكون مشتق جزئي من F فيما يتعلق ب -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error . نأخذ القيمة المتوسطة (mean()) نظرًا لأن error و x_train و y_train هما y_train للقيم ، a و b عبارة عن عدديتين.

المواد المستخدمة في المقال:

towardsdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html