🏽 👨🏾‍🏭 🚫 عدد الكامنة وراء الموسيقى الحديثة 🧜🏽 ⛵️ 🎣

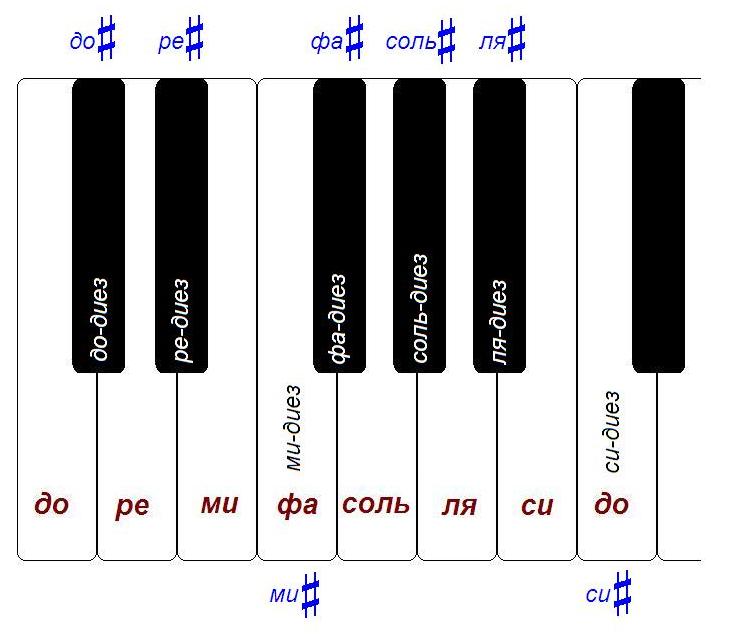
لماذا اثنا عشر؟

إذا نظرت إلى لوحة المفاتيح ، فسترى أن كل أوكتاف يحتوي على 12 نصف نغمة.
في حالة البيانو ، هذا يعني فقط أنه بين ، على سبيل المثال ، "إلى" أوكتاف الأول و "إلى" أوكتاف الثاني ، هناك 11 مفاتيح. جنبا إلى جنب مع واحد من "تفعل" (على سبيل المثال ، إلى اوكتاف الثاني) نحصل على 12 مفاتيح: تفعل # ، إعادة ، إعادة # ، ميل ، fa ، fa # ، الملح ، الملح # ، لا ، لا # ، سي ، تفعل.

لكن لماذا 12؟

ربما هذا مجرد حادث؟ أحب أسلافنا الرقم 12 ، ولديهم 12 في كل مكان: 12 شهرًا ، و 12 علامة زودياك ، و 12 من قبائل إسرائيل ، و 12 رسلًا ... وهنا قرروا ، فليكن 12 عامًا ، وهكذا تم الأمر. أم لا يزال هناك قانون موضوعي ، وهذا الرقم ليس عرضيًا؟

في هذه المقالة سأحاول إثبات أن هذا ليس حادثًا. المتطلبات العامة بما فيه الكفاية ، طبيعية تمامًا للموسيقى (الغربية) الحديثة ، مع ضرورة رياضية ، تقودنا إلى الرقم 12. ومن المثير للاهتمام أن السبب وراء وجودنا لهذه القيمة هو ملكية رقم آخر (انظر نهاية المقالة). يمكنك حتى أن تقول أنها تكمن في قلب الصوت الحديث.

بيان المشكلة

أولاً ، دعونا نحاول إضفاء الطابع الرسمي على المهمة.

لدينا تردد إشارة $\ omega_0$ . سوف نسميها منشط. لدينا أيضا اوكتاف مع تردد $2 \ omega_0$ . نحن الآن بحاجة إلى فهم الخيارات المتاحة للترددات الوسيطة $\ omega_0$ إلى $2 \ omega_0$ ، بحيث لحن مبني على هذه الملاحظات سوف يبدو متناغم لآذاننا؟

أخشى أن هذه الصيغة ، على الرغم من أنها تعكس جوهر السؤال ، لا تزال ، من وجهة نظر رياضية ، غامضة إلى حد ما ، ولا يمكن الإجابة على مثل هذا السؤال بشكل لا لبس فيه ، إذا كان لسماع الإنسان دقة محدودة للغاية. وهذا ما تؤكده حقيقة أنه في أوقات مختلفة تم استخدام الألحان المختلفة ، على سبيل المثال ، فيثاغورس ، والإيقاعات نظيفة ، المزاج جيدا ، والمزاج بالتساوي . وقد بدت جميعها سليمة ، على الأقل بالنسبة لبعض الأعمال ، مقبولة تمامًا.

ما هو الوئام؟

يجب علينا فرض بعض الشروط الإضافية. لكن أولاً ، يجب أن نجيب على سؤال مهم واحد: ما الذي نعتبره صوتًا متناغمًا؟

دعنا ننظر إلى صوتين - مع الترددات $\ omega_1$ و $\ omega_2$ .

خذ نسبة هذه الترددات. يمكن تمثيل هذه العلاقة كمنتج للأرقام $a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l}$ حيث $inline$ هي الأعداد الأولية ، و $inline$ - الأعداد الصحيحة ، على سبيل المثال ، هذه النسبة قد تساوي $2 ^ {- 3} \ cdot3 \ cdot5$ . ومن هذه الأعداد الأولية ( $inline$ ) أقل ، كلما كان هذا الفاصل أكثر تناسقًا بالنسبة لأذننا (سوف أجد هذا البيان هنا (انظر الفقرة الثانية) )

لذلك ، على سبيل المثال ، سيكون الصوت الأكثر تناسقًا وفقًا لهذا البيان عبارة عن أوكتاف (تغيير التردد بمقدار مرتين). وستكون الفواصل التوافقية التالية الخامسة (تغيير التردد في $inline$ مرات) ورباعي (تغيير التردد في $inline$ مرات).

ولكن ليس بهذه البساطة مع هذا البيان. لذلك ، على سبيل المثال ، ليس من الواضح جدًا كيف تؤثر الدرجة. على سبيل المثال ، ما هو الضرب أكثر انسجاما من قبل $inline$ او 7؟ لا أعرف ما إذا كان هذا السؤال قد تمت دراسته أم لا ، وهل من الممكن ، من حيث المبدأ ، تقديم إجابة عليه. أيضا ، تصور الانسجام هو شيء شخصي إلى حد ما. لذا ، فإن الموسيقى الحديثة مليئة بالأصوات التي كان من الممكن أن ينظر إليها على أنها نشوة رهيبة منذ 100-200 عام.

الشرط الأول. منشط ، كوارت ، كوينت ، اوكتاف

عدم اليقين هذا ليس مشكلة لأبحاثنا الصغيرة. والحقيقة هي أن الاستنتاج الوحيد الذي أريد استخلاصه من هذا البيان هو أنه في حالتنا ، على أي حال ، ينبغي أن يكون هناك على الأقل الفواصل "الأكثر تناسقًا" ، أي الأوكتاف والرباعية والخامسة. هذا هو ، جنبا إلى جنب مع منشط مع التردد $\ omega_0$ وأوكتاف مع تردد $2 \ omega_0$ يجب أن يكون لدينا أيضا الخامس والرابع ، مع ترددات على التوالي ${3 \ over 2} \ omega_0$ . ${4 \ over 3} \ omega_0$ أو شيء قريب جدا لم نتمكن من التمييز بين الخامس والرابع النقي.

ملاحظة: في الواقع ، فقط المقويات ، الأخماس والأوكتافات كافية. إن وجود خامس يعطينا فوراً الكوارت ، كإضافة إلى أوكتاف ، وبموجب الشرط الثاني (الثبات) ، الموصوف أدناه ، يجب أن يكون لدينا أيضاً ترتان منشط. أي أن الحاجة للرباعي هي نتيجة لوجود خامس وشرط الثبات.

وهذا هو الشرط الأول لدينا.

الشرط الثاني. ثبات

الشرط الثاني لدينا هو الثبات. وهذا مطلب مهم للموسيقى الحديثة. يتكون هذا المطلب من حقيقة أن جميع التناسقات في أي مفاتيح يجب أن تبدو هي نفسها. إذا كنا نتحدث عن النظام الحديث ، الذي يستخدم لضبط البيانو ، فإن هذا يعني أن الخامس ، الذي يتكون من سبعة نغمات ، يجب أن يبدو كما هو ، بغض النظر عن الصوت الذي تم بناؤه منه. وهذا يعني أن نسبة التردد بين فعل والملح يجب أن تكون هي نفسها بالنسبة لـ # - ملح # ، وإعادة - لا ، وإعادة # - لا # ، ... وعلى قدم المساواة $inline$ . ويجب أن ينطبق هذا الثبات ، بالطبع ، ليس فقط على الخامس ، ولكن أيضًا على أي فواصل زمنية. ميزة هامة لهذا النظام هي القدرة على تبديل المسرحية في أي فترة. هذا هو جوهر مزاج موحد.

يجب أن أقول إن هذا الشرط من الثبات ليس واضحًا جدًا ، وقد تم تطبيق هذا النهج مؤخرًا نسبيًا ، فقط في القرن الثامن عشر. الأنظمة المستخدمة من قبل (على سبيل المثال ، فيثاغورس ونقية) لا تملك هذه الخاصية. على سبيل المثال ، استمع إلى Sonata for Microtonal Piano (Ben Johnston) ، المكتوب في نظام نظيف (الحد الأولي = 5). يبدو وكأنه لم يتم ضبط البيانو. كل ثروات التوافقيات الحديثة تعتمد بالتحديد على هذا الثبات. على سبيل المثال ، ظهر "Bach-Cled Clavier" من Bach بدقة بفضل طريقة جديدة لضبط لوحات المفاتيح. لقد كان هذا الثبات هو الذي مكّن باخ من إنشاء تسلسلات توافقية كانت مستحيلة من قبل.

لذلك ، لدينا الآن جميع البيانات اللازمة لحساب.

حساب

دعونا نبني مقياسًا من المقويات إلى أوكتافات تفي بالمتطلبات.
لنفترض أنه في هذه الحالة نحصل عليها $inline$ الأصوات (بما في ذلك اوكتاف). إنه كذلك $inline$ وهو الرقم المطلوب. نريد أن نظهر ذلك $inline$ تحت ظروفنا يجب أن يكون 12.

نتيجة للمتطلب الثاني هو أن تكون الفترة الفاصلة بين ترددات الأصوات المجاورة متساوية $2 ^ {1 \ over N}$ .

الآن الشرط الأول يقول أنه في صفنا يجب أن يكون هناك صوتان يتوافقان مع ترددات (بتقريب جيد) ${3 \ over 2} \ omega_0$ و ${4 \ over3} \ omega_0$ . هذا هو الخامس والرابع. لنفترض أن الكوارت هو $inline$ يبدو في صفنا ، والخامس - $inline$ عشر. نحن نشير $inline$ .

من السهل أن نرى أن التغير في التردد بين الرابع والخامس (نسبة التردد) هو $inline$ .

ولكن ، وفقا لشرطنا الثاني ، يجب أن يكون هذا متساوًا أيضًا $2 ^ {n \ over N}$ .

لذلك حصلنا على الصيغة:

$2 ^ {n \ over N} \ approx 9/8$

بعد التحولات البسيطة ، نحصل على الصيغة الأساسية:

$n \ approx N (2 \ log_2 {3} - 3) = N \ cdot 0.170$

من السهل أن نرى أن الحل (بالطبع ، تقريبي) هو $inline$ حيث $inline$ - أي عدد طبيعي (صغير بما فيه الكفاية ، لأنه مع ذلك يختلف 0.170 عن 1/6).

دعنا ننظر إلى القضية $inline$ . في هذه الحالة $inline$ . $inline$ . وهذا هو ، وهذا هو البديل من النظام الحديث ، إلا من دون نصف نغمات ، فقط مع النغمات (تفعل ، إعادة ، ميل ، فا # ، الملح # ، لا # ، تفعل). ولكن ، كما ترون ، في هذه الحالة ، لم تدخل المجموعة الرباعية (و) والخمرة (الملح) في هذا النطاق.

وهذا هو ، قد يكون الخيار الوحيد بالنسبة لنا

$inline$ حيث $inline$ - أي عدد طبيعي ( $inline$ صغيرة بما فيه الكفاية). حالة $inline$ يتوافق فقط مع نظامنا الحديث ، والذي يسمى النظام المزاجي موحد.

ولكن لماذا لا 24 أو أكثر؟ السبب بسيط - يمكنني أن أفترض أن مثل هذا التخرج هو بالفعل مفرط لتصورنا. لذلك ، يبقى رقم واحد فقط: 12.

إذا لم تكن راضيًا عن قطار التفكير المعطى ، فيمكنك العثور عليه هنا

دليل رياضي دقيق

الهدف:

ابحث عن العدد الصحيح الموجب الأدنى N حيث يوجد عدد صحيح موجب $inline$ مثل هذا $2 ^ {n \ over N}$ يختلف عن $3 \ over2$ ليس أكثر من $\ دلتا$ سنتا .

الحل:

دلالة بواسطة $Z_n = N \ cdot (log_2 {3} -1)$ . ثم ، مع $\ delta <{1200 \ over N}$ (وهذا صحيح بالنسبة لمجموعة من هؤلاء $\ دلتا$ و $inline$ التي سننظر فيها) مهمتنا هي إيجاد الحد الأدنى $inline$ في أي

${{1200 \ over N} \ cdot | Z_n - round (Z_n) | <\ دلتا $$ .

حيث $inline$ - وظيفة التقريب إلى أقرب عدد صحيح.

سوف نحل هذه المشكلة عدديا.

الآن حان الوقت لاتخاذ قرار $\ دلتا$ .

ما مقدار التباين (الخامس) بين الخامس الخالص و "الخامس لدينا" الذي نعتبره مقبولاً؟ يسمع الكثير من الناس ، على سبيل المثال ، أن الثلث الكبير / الصغير في النظام المزيف بالتساوي "مزيف". ولكن هذا هو فقط حوالي 15 سنتا بالنسبة لفترات نقية. لذلك ، يجب أن يكون شرطنا أفضل من 15 سنتًا. تقول بعض المصادر أنه في بعض الترددات ، يميز الموسيقيون ما يصل إلى 5 - 6 سنتات. لذلك من الحكمة أن تأخذ $$ \ دلتا = 5 دولارات$ .

ثم يبين الجدول بوضوح أن الأصغر $inline$ . التالية مرضية $inline$ .

ملاحظه:
التكرار التالي ، لكل منهما $inline$ تحتاج أيضًا إلى التحقق من الصوت وفواصل زمنية أخرى. في حالة $inline$ على سبيل المثال ، يصبح الثلثان "مزيفين" تمامًا: أكثر من 30 سنتًا (لثلث كبير).

إذن إجابتنا هي: $inline$ . الذي كان مطلوبا لإثبات.

وبالمناسبة ، من الواضح أن إجابتنا لن تتغير إذا قمنا بدلاً من ذلك $$ \ دلتا = 5 دولارات$ خذ على سبيل المثال ، 10 أو حتى 15.

الاستنتاج. الرقم الأساسي

من المثير للدهشة ، أنه تبين أن العدد الأساسي للنظام الموسيقي الحديث والموسيقى المعاصرة (الأوروبية) هو $\ log_2 {3}$ ، أي أنه مع دقة جيدة (0.1 ٪) تحمل المساواة التالية:

$\ log_2 {3} \ approx 19/12$

ردود على التعليقات والنقد في التعليقات

بادئ ذي بدء ، شكرا لتعليقات مثيرة للاهتمام!
فيما يلي إجاباتي على أهم التعليقات (في رأيي) والانتقادات.

نقد 1. بيضة أو دجاج

Druu: أنظر ، 12 صوتًا في أوكتاف كان يصل إلى مزاج موحد بشكل عام ، لذلك لا يمكنك تبرير 12 صوتًا بمساعدة المزاج ، فهذا سيكون مجرد خطأ.

المخبأ: هذا هو بالضبط منطق الرنين الذي أتحدث عنه: إذا اخترت موسيقى مبنية على نظام معين ، فمن الواضح أنه في سياقها يكون نظام مختلف مستحيلاً.

لهذه الملاحظات وما شابهها ، أود أن أذكر 2 من المواقف المضادة:

1) إذا بدقة كافية المساواة $log_2 {3} = 19/12$ ، سيكون من المستحيل "سحب" نظام مزاج موحد في نظام نقي يتكون من 12 صوتًا. الأقوى $log_2 {3}$ يختلف عن $inline$ ، أكثر كاذبة لدينا الخامسة سوف يبدو. إذا كان هذا الرقم مختلفًا (بقوة) ، فلن يكون هناك نهج مزاجي موحد لفترات نقية ، ونتيجة لذلك ، لن يكون هناك موسيقى حديثة ، أو لنقول ، سيكون مختلفًا. لذلك ، الاستنتاج أن خصائص الرقم منطقية للغاية $log_2 {3}$ هي أساس الموسيقى الحديثة.

2) من المستحيل تبرير الحجة المضادة الثانية ، وهي مجرد افتراض ، لكن يبدو لي أن كل هذا المنطق يستحق الاهتمام. دعنا نحاول الإجابة على السؤال ، لماذا نشأت على الإطلاق الحاجة إلى نظام مقسى موحد؟ التعليقات قد أجبت بالفعل جزئيا. الموسيقى في ذلك الوقت (وقت إنشاء نظام مزاجي موحد) استخدمت بالفعل التحويرات وتعدد الأصوات ، والتي في الواقع ، إلى حد كبير ، تتطلب بالفعل مزاج موحد. تم حل مشكلة الصوت "وهمية" من خلال حقيقة أن الموسيقيين قليلا "ضبط" الصوت أثناء الأداء. كان من السهل القيام بالسلسلة (على الأقل بدون تردد) والرياح والغناء (صحيح ، إذا كنت مخطئًا - لقد توصلت إلى هذا الاستنتاج من تعليقاتك). على سبيل المثال ، بالنسبة للكمان - هذا مجرد تغيير بسيط في موضع الأصابع. ولكن بمجرد حرمانك من هذه الفرصة (harpsichord) ، بدأ كل شيء على الفور في أن يبدو سيئًا. لذا ، يبدو أن هذه الملاحظات الـ 12 لم تظهر على هذا المنوال فحسب ، ولكن كتطور طبيعي للموسيقى تجاه هذه الإمكانية للتضمينات المجانية وتعدد الأصوات الغنية ، وهذا بدوره نتيجة للثبات. كان تطور طبيعي للموسيقى. بمعنى ، أريد أن أقول أنه إذا كان من الممكن حدوث ثقل رياضي ليس لـ 12 صوتًا ، ولكن على سبيل المثال ، لمدة 10 ، سيكون لدينا (حتى قبل المزاج الموحد) في مقياسنا 10 أصوات (في هذه الحالة ، أنا أتحدث عن الطريقة تطوير الموسيقى الأوروبية). ثم يتم سحب 10 أصوات مزاج موحد على نظامنا النقي.

نقد 2. تفرد الاثني عشر

كان هناك الكثير من الانتقادات حول الادعاء بأن 12 هو الرقم المعقول الوحيد.

أولاً ، لفهم عدوانية هذا البيان ومبدأ استحالة تبرير صارم ، ربما قللت درجة تصنيف بعض الادعاءات الواردة في المقال. وبعد ...

في هذه الحالة ، لدينا 2 خطوط النقد.

1) لماذا أعتبر أن 19 أو 24 أو 29 (وما إلى ذلك) غير مقبول؟

لا ، لا أعتقد ذلك. بالنسبة للأدوات المختلفة ، هناك تقنيات لاستخدام الأصوات خارج المقياس ، على سبيل المثال ، glissando و vibrato. هذه التقنيات تضيف الجمال والطبيعية إلى الصوت. لذلك ، حتى مع وجود 12 ملاحظة ، لا نزال نستخدم الأصوات المساعدة. إذا كنا نتحدث عن محيط ، وعن صوت غير عادي ، وعن تخصيب الصوت ... فهذا أمر له ما يبرره ، ولكن إذا كنا نتحدث عن النغمات الأساسية ، فإن لدي شكوك. يتم إنشاء الموسيقى ليس فقط للنخبة ، ولكن للناس العاديين ، وبالنسبة لهم هذا التخرج (IMHO) ليس ضروريًا.

الحجة الثانية ، والتي تم تقديمها في التعليقات ، هي في الواقع تعقيد إنشاء الأدوات والأداء في حالة النطاق الطويل ، على الرغم من أن لدينا مثالًا رائعًا على مثل هذه الأداة - السيتار. ولكن حاول أن تأخذ أوكتافًا (بيد واحدة) على البيانو إذا كان لديك 24 صوتًا.

2) لكن ماذا عن الخماسي؟

في جميع البلدان الشرقية التي كنت فيها ، لسبب ما نادراً ما سمعت موسيقى وطنية مبنية على مقياس خماسي. كما قام جميع الموسيقيين من الشرق ، الذين استمعت إليهم (وأحب بعضهم) ، بأداء الموسيقى الأوروبية تمامًا. فيما يلي اقتباس مثير للاهتمام: "يستخدم الملحنون الأكاديميون خماسيًا كطلاء خاص منذ القرن التاسع عشر لإعطاء الموسيقى نكهة قديمة." رائحة عتيقة ...
في تصوري ، مع ذلك ، هذه الموسيقى ليست حديثة ، لكنني لا أريد أن أدافع عن هذا الموقف ، لذلك في بعض الأماكن في المقال أستخدم مصطلح "الموسيقى الأوروبية الحديثة". من الواضح أن هذه الموسيقى (المبنية على مقياس الخماسي) تطورت وفقًا لقوانين أخرى ، ولم تصل إلى الطلب على تعدد الأصوات الغنية والتشكيل المتكرر والسهل ، والتي ظهرت في الموسيقى الأوروبية. لذلك ، من الواضح أن هذه المقالة ليست عن الخماسي.

نقد 3. الموسيقى المعاصرة

ماذا أسمي الموسيقى الحديثة؟

على الرغم من أن هذا يبدو كأنه علم موسيقى ، إلا أنه يعني بالموسيقى الحديثة الموسيقى التي تتطلب الثبات ، الأمر الذي يؤدي في حالة الآلات ذات النظام الثابت (على سبيل المثال ، harpsichord ، البيانو) إلى الحاجة إلى نظام معتدل بشكل موحد (أو شيء قريب). في حالة الأدوات الأخرى ، على سبيل المثال ، الأوتار الخالية من التوتر ، يبدو كل شيء أكثر تعقيدًا ، لأنه في الواقع ، من الممكن استخدام مجموعة أكبر من (12) من الأصوات. ولكن لا يزال ، عندما نتحدث عن شرط الثبات ، فإننا نعني أن هذه الأصوات يجب أن تكون قريبة جدًا (بتردد) من 12 لدينا.

يشمل هذا التعريف كل موسيقى البيانو تقريبًا والموسيقى الكلاسيكية الأوروبية والجاز وموسيقى الروك والبوب وجميع المشتقات منها. أنا متأكد من أن هناك استثناءات ، ولكن IMHO هذه هي الاستثناءات. لا أرى أي سبب للتجادل حول هذا ، لأنه يمكن للجميع استثمار شيء في هذا المفهوم.

النقد 4. حساب

خطأ في الحسابات.

أعتقد أنه تمت إزالة هذا السؤال. ومع ذلك ، لا بد لي من الاعتراف بأنه خلال المناقشة ، أدليت بعدة بيانات خاطئة عن المسائل الثانوية التي لم تؤثر على الاستنتاج الرئيسي للمقال.

ملاحظة: لا تعامل هذه المقالة (وجعل المتطلبات المقابلة) بمثابة عمل أكاديمي. :) هذه ليست مقالة عن نظرية الموسيقى. علاوة على ذلك ، هذه ليست مقالة عن تاريخ الموسيقى. في هذه المجالات ، لا أعتبر بأي حال من الأحوال معرفتي مهمة على الأقل إلى حد ما وأعترف بأنه قد تكون هناك أخطاء ، على الرغم من أنني حاولت تجنبها. هنا يتم صياغة مشكلة رياضية بسيطة (على مستوى المدرسة من التعقيد) ، والحل الذي ، كما يبدو لي ، له تفسير مثير للاهتمام. التي شاركت.

عدد الكامنة وراء الموسيقى الحديثة