الوقت القاتل من الطفولة

أنا متأكد من أن العديد من القراء يشاركون أحيانًا في هراء عديم الفائدة في الفصل بدلاً من الاستماع إلى المعلم. لقد فعلت ذلك بالضبط ، وكانت إحدى الطرق لقتل الوقت هي اللعب على الورق. بدت لعبة المعاينة (التي لا يزال اسمها غير معروف بالنسبة لي) مثيرة للاهتمام بشكل خاص بالنسبة لي ، ولكن هناك سببان: لا يتطلب الأمر وجود شخص ثانٍ ويمكن إكماله! صحيح ، كان من النادر للغاية القيام بذلك. لوقت طويل كنت أتساءل عن مدى بساطة الحل ، والآن ، بعد سنوات عديدة ، لن يكون من الصعب العثور عليه بشكل برمجي.

القواعد

أولاً ، يجدر وصف القواعد. تبدأ اللعبة بالحقل التالي:

123456789
111213141
516171819

هنا ، يتم تسجيل جميع الأرقام من 1 إلى 19 حرفًا بحرف ، باستثناء 10. الأرقام موجودة من اليسار إلى اليمين ، سطراً سطراً. القواعد بسيطة للغاية - في كل خطوة تحتاج إلى شطب رقمين يتوافق مع المعايير التالية:

• يجب أن تكون الأرقام هي نفسها أو في المجموع تعطي 10 (1 و 1 و 3 و 7 و 8 و 2 ، إلخ) ؛
• يجب عليهم إما الوقوف فوق بعضهم البعض أو ترتيبهم في سلسلة. في هذه الحالة ، يتم تجاهل الأرقام التي تم شطبها بالفعل.

يظهر أحد خيارات التحركات القليلة الأولى أدناه:

1 23456789
1 11213141
5161718 19

#2345678 9
# 1 1213141
5161718##

#2345678#
##1213141
5161718##

في الوقت الذي لا يوجد فيه المزيد من التحركات ، تتم إضافة جميع الأرقام غير المميزة إلى النهاية. تنتهي اللعبة عندما يتم شطب الحقل بالكامل.

#2345678#
##1213141
51 6 171 8 ##
23 4 567 8 12
131415161
718

#2345678#
##1213 1 41
5 1 # 1 71###
23#567#12
131415 1 61
718

#2345678#
##1213#41
5###71###
2 3 #567#12
1 3 1415#61
718

...

عدد التحركات المتاحة يزداد بسرعة ، تبدأ اللعبة في التفرع بقوة. غالبًا ما يصبح الجدول طويلًا بحيث يمتد إلى الصفحة التالية في دفتر ملاحظات. من الأسهل بدء مجموعة جديدة. في بعض الأحيان كنت أتواصل من المثابرة ، لكنني في النهاية تنازلت.

يثير هذا السؤال المعقول - ما مدى سرعة الانتهاء من هذه اللعبة؟ في مرحلة الطفولة ، كان من الممكن إيجاد حل في عمود واحد على ورقة دفتر الملاحظات - أي حوالي 40 سطرًا أو 360 حرفًا.

لا أعرف الطريقة المضمونة لإكمال اللعبة. ليس من الواضح تماما كيفية اختيار استراتيجية. يمكنك تجربة اللعب بنفسك إذا لم تفعل ذلك.

قرار

كيف يتم البحث عن حلول لهذه المشاكل؟ أنا لا أعرف بالتأكيد ، لكنني اخترت تمثال نصفي المعتاد.

نحتاج إلى قائمة انتظار ، تتكون أولاً من تكوين أولي واحد. في كل خطوة ، نأخذ التكوين التالي من قائمة الانتظار ، وننظر في جميع التحركات المتاحة منه ، وإما أن نضيفها جميعًا إلى نهاية قائمة الانتظار أو نعلن أنفسنا الفائز إذا لم تكن هناك مثل هذه التحركات.

123456789 #23456789 12345678# 123456789 123456789 123456789 123456789 ...
111213141 #11213141 #11213141 ##1213141 1##213141 11#213141 11121314# ...
516171819 516171819 516171819 516171819 516171819 516#71819 51617181# ...

إذا لم تفصل في الحل الأول المتاح ، فستنتج هذه الخوارزمية جميع الحلول الممكنة (في وجود كمية لا حصر لها من ذاكرة الوصول العشوائي).
في الممارسة العملية ، لن يساعد هذا النهج الساذج على الإطلاق ، على الأقل بسبب التكرارات التي تظهر باستمرار في قائمة الانتظار. لذلك ، ستكون هناك حاجة لبعض التحسينات ، والتي سأشرحها الآن:

• بطبيعة الحال ، تحتاج التكوينات إلى التخزين المؤقت حتى لا تعيد ترتيبها. سيؤدي ذلك إلى زيادة استخدام الذاكرة بشكل كبير ، ولكنه لا يساعد في الحصول على حل في فترة زمنية معقولة. علاوة على ذلك ، فإن مسألة مقارنة التكوينات تظهر بحدة. نظرًا لأن تكوينين فائزين من نفس الحجم سيتألفان دائمًا من أرقام يتوسطه خط ، هناك حاجة إلى طريقة إضافية للتمييز بينهما ، وإلا فلن يتم العثور على جميع الحلول ؛
• لجعل البحث ذا معنى وسريع ، من الأفضل استخدام قائمة انتظار الأولوية. بعدد أقل من الأرقام الموجودة في الحقل (بما في ذلك تم شطبها) ، يجب مراعاة التكوين السابق ؛
• إذا كنت بحاجة إلى أكثر من حل واحد ، ولكن كثيرًا ، فمن الأفضل تحديد الحد الأقصى لعدد الأرقام في الحقل ، سيصدر البحث حلولًا قبل ذلك بكثير.

الجواب

إذا كان كل شيء صحيحًا ، اتضح أن الحل الأدنى يتكون من 68 حرفًا فقط أو 8 أسطر!

سأحضرها في شكل رسوم متحركة متحركة. تم لصق بعض التحركات في خطوة واحدة لتقليل عدد الإطارات:

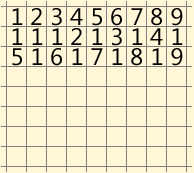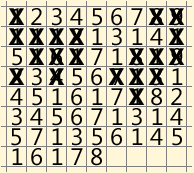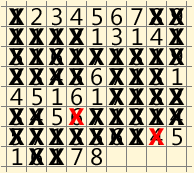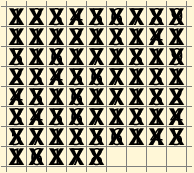
أنا صادقة ، أدهشني مدى قصر هذا القرار. ولكن ربما لن يتحقق هذا الحظ والقرارات الأخرى قريبًا وستكون طويلة جدًا؟

لا ، القرارات ليست نادرة على الإطلاق. تم العثور على إجابات سريعة في أطوال 72 و 74 و 76. و 4 حلول مختلفة بشكل أساسي بطول 80. بشكل عام ، تمكنت من العثور على 30 حلًا يصل طولها إلى 90 طولًا (شاملة) ، وإذا قمت بزيادة الحد إلى 100 ، فسيكون هناك 170 حلًا. ولكن البحث عنها يصبح أكثر تكلفة.

تحت المفسد ، يتم وصف الحل الأمثل بالتفصيل:

 123456789 111213141 516171819 123456789 111213141 5161718## 123456789 1##213141 5161718## 12345678# 1##21314# 5161718## #2345678# ###21314# 5161718## #234567## ####1314# 5161718## #234567## ####1314# 5161718## 234567131 45161718 #234567## ####1314# 51#1718## 23#567131 45161718 #234567## ####1314# 51#171### #3#567131 45161718 #234567## ####1314# 51#171### #3#567#31 451617#8 #234567## ####1314# 51#171### #3#56###1 451617#8 #234567## ####1314# 5###71### #3#56###1 451617#8 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 571356145 16178 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 57#356145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 5###56145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 #####6145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 34567131# ######145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 3456713## #######45 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 3#56713## #######45 1##78 #234567## ####1314# 5###71### #3#56###1 451617### 3#56713## #######45 1##78 #234567## ####1314# 5###71### #3#56###1 45161#### ##56713## #######45 1##78 #234567## ####1314# 5###7#### #3#56###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# 5######## ###56###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##56##### #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##5###### ########5 1##78 #234567## ####1314# ######### ####6###1 45161#### ######### ######### 1##78 #234567## ####131## ######### ########1 45161#### ######### ######### 1##78 #234567## ####13### ######### ######### 45161#### ######### ######### 1##78 #234567## #####3### ######### ######### 4516##### ######### ######### 1##78 #23456### ######### ######### ######### 4516##### ######### ######### 1##78 #2345#### ######### ######### ######### #516##### ######### ######### 1##78 #234##### ######### ######### ######### ##16##### ######### ######### 1##78 #23###### ######### ######### ######### ##1###### ######### ######### 1##78 #23###### ######### ######### ######### ######### ######### ######### ###78 #2####### ######### ######### ######### ######### ######### ######### ####8 ######### ######### ######### ######### ######### ######### ######### ##### 

يمكن الاطلاع على رمز حل Java الخاص بي على هذا الرابط ، لكني أحذرك من أنه أمر فظيع ، لأنه كتبت أصلا لا للنشر. في شكله الحالي ، يجد كل الحلول ما يصل إلى 70 حرفًا (أي حل واحد فقط). هذا سهل الإصلاح عن طريق اللعب بالشروط الموجودة في التعليمات البرمجية.

شكرا لاهتمامكم!