حب الرياضيات

استنادا إلى مقال بقلم جوليان كلينتون سبروت. نماذج ديناميكية من الحب. ديناميات علم اللاخطية وعلوم الحياة ، أغسطس 2004.

اعتقدت الوئام في الجبر ...
نظرية صديقي جافة ، لكن شجرة الحياة دائماً خضراء ...

الذين فقط لم يقاتلوا من أجل هذه "المشكلة" .... لقد تم تفكيكها في المآسي اليونانية القديمة ، كما أخبرنا شكسبير العظيم قصة روميو وجولييت ، وقام أندريه وجدة بتفكيكها من كلا الجانبين في تشريح الحب. لكن الناس لم يصلوا إلى أسفل الحقيقة حتى اتخذ العلماء القرار. صحيح ، ليس كل شيء يبدو مقنعًا تمامًا لعلماء النفس. هم أنفسهم في بعض الأحيان حتى بعد الطلاق الخاصة بهم تبدأ في تحليل تاريخ حبهم غادرت. حسنًا ، اكتب كتبًا تشبه الكعك الساخن أحيانًا. مكتوبة من قبل الخبراء! ماذا يمكنني أن أقول؟ لا شيء تقريبا الشخصية - الأعمال فقط ...

وأخيرًا ، لم يأخذ الشعراء بالكتاب والشعراء بالحب. الرياضيات هي ملكة العلوم. هل هي قادرة على مواجهة مشكلة أبدية؟ يتم نشر الكتب ، على سبيل المثال ، عن طريق جون جوتمان ، "رياضيات الزواج" ، وغيره من المؤلفين. يعتبر علماء الرياضيات تطوير العلاقات الرومانسية عملية ديناميكية ...

وكل شيء يبدأ ، كما هو متوقع ، بالتعريفات. كيفية التعرف على الحب نوعيا وكميا؟ يصنف الباحثون المشكلة حسب النوع: علاقة غرامية ، شغف ، إخلاص. علاوة على ذلك ، كل نوع لديه مجموعة معقدة من المشاعر. ولكن بالإضافة إلى حب شخص آخر ، هناك حب للذات وللحياة وللإنسانية ...

في الوقت نفسه ، لا يمكن عكس نقيض الحب - في النموذج الرياضي - لأن كلا المشاعر يمكن أن تتعايش في نفس الوقت. على سبيل المثال ، قد يعجب شخص ما ببعض مظاهر شريك ، ولكن قد يكون البعض الآخر سيئًا. لذلك ، من غير الواقعي افتراض أن حب الفرد لا يتأثر إلا بمشاعره الخاصة ، وأن مشاعر الشريك الآخر لا تعتمد على التأثيرات الأخرى ، وأن المعلمات التي تميز تفاعل شخصين تظل دون تغيير ، وبالتالي تستبعد إمكانية التعلم والتكيف.

يزيد التعقيد حتى في نموذج محدود مقيد بشكل كبير عندما يتم إدخال ثلاثة أو أكثر من المتغيرات في معادلات اللاخطية و / أو.

* ملاحظة: مترجم. في رأيي ، يمكن لهذه الدراسات أيضًا إحياء الرياضيات نفسها ، وجذب انتباه الجمهور ، وعادة ما تكون بعيدة عن هذا العلم التجريدي.

نموذج خطي بسيط

يمكن تمثيل قصة حب روميو وجولييت في الوقت (ر) باستخدام الدالات * R (ر) - حب روميو لجولييت وجي (ر) - حب جولييت لروميو.

ثم يتم التعبير عن نموذج خطي بسيط لعلاقتهم بالمعادلات (1)



أ و ب - معايير النمط الرومانسي لروميو
ج و د - خيارات أسلوب جولييت
يميز كيف انغمس روميو في مشاعره الخاصة
ب - إلى أي مدى اعتنق روميو مشاعر جولييت

تستخدم إحدى المقالات (جوتمان وآخرون ، 2002) مصطلح "الجمود السلوكي" لأول و "وظيفة التأثير" للمعلمة الثانية. على الرغم من 0 = ، يصبح القصور الذاتي أكبر. النموذج الديناميكي في مثل هذه الظروف هو ثنائي الأبعاد ويمكن التحكم فيه من خلال الشروط الأولية والمعلمات الأربعة ، والتي يمكن أن تكون إيجابية أو سلبية.

اقترح رينالدي نموذجًا خطيًا بسيطًا ، 1998 أ. في الوقت نفسه ، تتم إضافة مصطلح مجاني لكل مشتق من أجل مراعاة الجاذبية (أو الكراهية ذات القيمة السلبية) ، والتي يظهرها كل شريك للآخر في غياب مشاعر أخرى. مثل هذا النموذج أكثر واقعية لأنه يسمح للمشاعر أن تنمو من حالة عدم مبالاة وتوفر توازنًا لا يتميز باللامبالاة التامة. كل هذا موصوف بهذه الطريقة فقط عن طريق إدخال معلمتين إضافيتين. في حين أن حالة التوازن غير اللامبالاة يمكن أن تكون مهمة للغاية بالنسبة للأفراد المعنيين ، فإن هذا لا يغير الديناميكيات إلا عن طريق تحريك مساحة الولاية RJ.

الأساليب الرومانسية

يمكن لروميو أن يعرض أحد الأساليب الرومانسية الأربعة اعتمادًا على اللافتات أ و ب ، مع التدوين الذي قدمه مؤلف العمل (Strogatz ، 1994) وطلابه:

1. رغبة عاطفية: a> 0، b> 0 (يلف روميو بمشاعر جولييت ومشاعرها.)
2. النوع النرجسي: a> 0، b <0 (روميو محاط أكثر بمشاعره الخاصة ، إنه منفصل عن مشاعر جولييت.)
3. حذر (أو حبيب موثوق به): a <0، b> 0 (يتحرك روميو بعيدًا عن مشاعره الخاصة ، ولكن تغلب عليها مشاعر جولييت.)
4. الناسك: a <0، b <0 (تم فصل روميو عن مشاعر جولييت ومشاعرها.)

نظرًا لأن أربعة أنماط من السلوك ممكنة أيضًا لجولييت ، فهناك 16 مجموعة ممكنة من الأزواج ، لكل منها دينامياتها الخاصة ، على الرغم من أن نصفها يتوافق مع التقليب من R و J.

تحدد المعادلات (1) نقطة توازن واحدة لـ R = J = 0 ، والتي تقابل علاقة غير مبالية متبادلة ، أو ما يسمى "هضبة الحب" (في نموذج رينالدي ، 1988) ، مع وصف للسلوك من خلال القيم الذاتية (2)




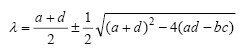
التركيز Forking السرج
التين. 1. الوضع الديناميكي بالقرب من نقطة التوازن في الفضاء ثنائي الأبعاد ، وفقًا للمعادلة 1.

مثلث الحب

يتم الحصول على نموذج أكثر ثراءً من الناحية الرياضية عند إضافة شخص ثالث إلى نموذج بسيط ، خاصةً لأن التحالفات قد تنشأ والتي يمكن لشخصين أن يتحدوا ضدها. لنفترض أن روميو لديه حبيب آخر ، هو جينيفيف ، على الرغم من أن الشخص الثالث المعني قد يكون طفلًا أو قريبًا آخر. في هذه الحالة ، يصبح فضاء الحالات أكثر ترجيحًا من حيث الأبعاد ، حيث يكون لكل من الثلاثة مشاعر تجاه الاثنين الآخرين ، وتنشأ اثنتا عشرة معلمة إذا كان بإمكان كل منهما أن يأخذ أنماطًا مختلفة بالنسبة إلى الآخر ، حتى لو تم تجاهل الجذب الطبيعي ، ( استعرضها رينالدي ، 1998 أ).

في أبسط الحالات ، قد لا تعرف جولييت وجنيفيف وجود بعضهما البعض ، وقد يعرض روميو نفس الأسلوب الرومانسي فيما يتعلق بكليهما. بعد ذلك يتحول النظام الناتج عن الأبعاد الأربعة إلى نظامين مقسومين ثنائي الأبعاد ، إلى أن تتأثر مشاعر روميو تجاه جولييت بطريقة ما بمشاعر جينيفيف بالنسبة له ، وينطبق الشيء نفسه على جينيفيف.

آثار غير الخطية

هناك عدد لا حصر له من الطرق لإدخال تأثيرات غير خطية. تخيل أن روميو يستجيب بشكل إيجابي لمحبة جولييت ، ولكن مع مظهر مفرط من حبها ، يشعر كما لو كان خنقا ويظهر رد فعل سلبي. بالمقابل ، إذا أظهرت جولييت ما يكفي من الكراهية ، فيمكن لروميو أن تحاول أن تكون ممتعًا لها.

في هذه الحالة ، يمكن الاستعاضة عن bJ في المعادلة 1 بالوظيفة اللوجستية bJ (1 - | J |) المقابلة لقياس J بالوحدات من الشرط الذي يقابلها J = 1 بالقيمة التي يصبح عندها حبها نتائج عكسية. النتائج المماثلة من الناحية النوعية تأتي من الوظيفة bJ (1 - J2) ، وهي الحالة التي نظرت فيها رينالدي (1998b) للشاعر الإيطالي في القرن الرابع عشر نموذج الحب الأفلاطوني للورا الجميلة ، التي تربطها بالزواج. على افتراض الشيء نفسه بالنسبة لجولييت ، نحصل على:
(4)



هناك 4 حالات التوازن ، بما في ذلك واحدة في الأصل. ويبين الشكل 3 التركيز المستمر الذي جولييت. ك "رغبات عاطفية" (ج = د = 1) يقود روميو "الناسك" (أ = ب = –2) إلى حالة من الحب المتبادل في R = J = 2. نموذج مماثل لمحبي حذرين (موثوقة) مع اللاخطية السيني يؤدي أيضا إلى توازن مستقر (رينالدي وجراناني 1998). من الواضح أن المعادلات 4 لا تسمح بدورات الحد ، ولا تحدث الفوضى بينما يكون النظام ثنائي الأبعاد.


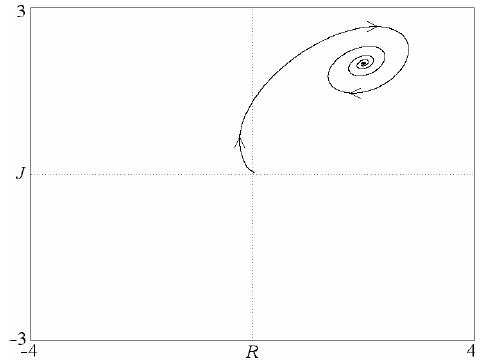التين. 3. أحد الحلول للنموذج اللاخطي وفقًا للمعادلة 4.

ربما تطبيق تأثيرات غير خطية على مثلثات الحب.

خاتمة

تُظهر بعض النماذج الديناميكية الخطية للحب ديناميات معقدة بشكل مدهش ، بينما يبدو أن الكثير منها يشبه التجربة المعروفة في العلاقات. إذا كان هناك ثلاثة أو أكثر من المتغيرات وحتى يتم إدخال أبسط الآثار غير الخطية ، يمكن أن تحدث الفوضى. يمكن تخيل امتداد مثير للاهتمام للنموذج عند النظر في مجموعة من الشخصيات المتفاعلة ، على سبيل المثال ، في حالات الأسرة الكبيرة أو البلدية. هذه النماذج ، بالطبع ، مبسطة للغاية ، لأن الحب يؤخذ في الاعتبار كمتغير عددي بسيط ، وردود فعل الأفراد فيما يتعلق بحبهم وحب الشخصيات الأخرى لهم متسقة وآلية ، دون مراعاة عوامل التأثير الخارجي.

ملاحظة: الحب يمكن أن يعيش بدون رياضيات ، لكن الرياضيات تثير حب الذات للأشخاص الذين يقدرون الانسجام الحقيقي.

المراجع:
جوليان كلينتون سبروت. نماذج ديناميكية من الحب. ديناميات اللاخطية علم النفس وعلوم الحياة • أغسطس 2004

رينالدي ، س. (1998 أ). حب ديناميات: حالة الأزواج الخطية. الرياضيات التطبيقية والحساب ، 95 ، 181-192.
Rinaldi، S. & Gragnani، A. (1998). حب الديناميات بين أفراد آمنين: نهج النمذجة. الديناميات غير الخطية وعلم النفس وعلوم الحياة ، 2 ، 283-301.
Rinaldi، S. (1998b). لورا وبيترارك: قضية مثيرة للاهتمام لديناميات الحب الدورية. مجلة SIAM في الرياضيات التطبيقية ، 58 ، 1205-1221