الاستدلال المتغير - ما هو وماذا يأكل؟

مرحبا يا هبر!

لقد تحدثت مؤخرًا مع زملائي حول أداة تشفير ذاتي تبايني ، واتضح أن الكثير من أولئك الذين يعملون في التعلم العميق يعرفون عن الاستدلال المتغير (التباين المتغير) ، ولا سيما الحد الأدنى للتغير من خلال الإشاعات ولا يفهمون تمامًا ما هو عليه.
في هذه المقالة أريد تحليل هذه القضايا بالتفصيل. من يهتم ، أطلب قطعًا - سيكون الأمر ممتعًا للغاية.

ما هو الاختلاف الاختلاف؟

حصلت عائلة الأساليب المختلفة للتعلم الآلي على اسمها من قسم التحليل الرياضي "حساب التفاضل والتكامل التفاضلي". في هذا القسم ، ندرس مشاكل البحث عن الحد الأقصى للوظائف (دالة هي دالة للوظائف - أي أننا لا نبحث عن قيم المتغيرات التي تصل فيها الوظيفة إلى الحد الأقصى (الحد الأدنى) ، ولكن هذه الوظيفة تصل فيها الوظيفة إلى الحد الأقصى (الحد الأدنى).

ولكن السؤال الذي يطرح نفسه - في التعلم الآلي ، نحن نبحث دائمًا عن نقطة في مساحة المعلمات (المتغيرات) التي تكون فيها وظيفة الخسارة أدنى قيمة. وهذا هو ، مهمة التحليل الرياضي الكلاسيكية ، وهنا هو حساب التفاضل والتكامل من الاختلافات؟ يظهر حساب الاختلافات في الوقت الحالي عندما نقوم بتحويل وظيفة الخسارة إلى دالة خسارة أخرى (غالبًا ما يكون هذا هو الحد الأدنى للتغير) باستخدام طرق حساب التفاضل والتكامل.

لماذا نحتاج هذا؟ أليس من الممكن تحسين وظيفة الخسارة مباشرة؟ نحتاج إلى هذه الطرق عندما يكون من المستحيل الحصول مباشرة على تقدير تدرج غير متحيز (أو يكون لهذا التقدير تشتت مرتفع للغاية). على سبيل المثال ، مجموعات النموذج لدينا $$$p (z)$ و $$$p (x / z)$ ، ونحن بحاجة إلى حساب $$$p (x) = \ int (p (z) p (x / z) dz)$ . هذا هو بالضبط ما تم تصميم التشفير التلقائي لصيغته.

ما هو الحد الأدنى المتغير؟

تخيل أن لدينا وظيفة $$$f (x)$ . سيكون الحد الأدنى في هذه الوظيفة أي وظيفة $$$g (x)$ تلبية المعادلة:

$$

$$g (x) <= f (x)$$

هذا هو ، لأي وظيفة هناك حدود أقل لا تعد ولا تحصى. هل كل هذه الحدود السفلية متشابهة؟ بالطبع لا. نقدم مفهومًا آخر - التناقض (لم أجد مصطلحًا ثابتًا في أدب اللغة الروسية ، وتسمى هذه القيمة الضيق في مقالات باللغة الإنجليزية):

$$

$$\ delta = الحد الأقصى {f (x)} - الحد الأقصى {g (x)}$$

من الواضح بما فيه الكفاية ، المتبقية دائما إيجابية. أصغر المتبقية ، كان ذلك أفضل.

فيما يلي مثال للحد الأدنى مع صفر المتبقية:

وإليك مثال صغير متبقي ولكنه إيجابي:

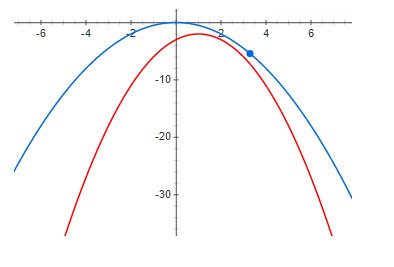
وأخيرا ، هناك تباين كبير بما فيه الكفاية:


يمكن أن نرى بوضوح من الرسوم البيانية أعلاه أن الحد الأقصى للدالة والحد الأقصى للحد الأدنى في نفس النقطة عند الصفر المتبقي. أي إذا أردنا إيجاد الحد الأقصى لبعض الوظائف ، فيمكننا البحث عن الحد الأقصى للحدود. إذا كان التناقض ليس صفراً ، فهذا ليس كذلك. والحد الأقصى للحد الأدنى يمكن أن يكون بعيدًا جدًا (على طول المحور السيني) عن الحد الأقصى المطلوب. توضح الرسوم البيانية أنه كلما بقيت أكبر ، كلما كانت الارتفاعات أعلى من بعضها البعض. هذا غير صحيح بشكل عام ، ولكن في معظم الحالات العملية يعمل هذا الحدس بشكل جيد للغاية.

متغير التشفير التلقائي

سنقوم الآن بتحليل مثال على حد أدنى جيد جدًا للتغير مع وجود بقايا صفرية محتملة (أدناه سيكون من الواضح سبب ذلك) - هذا هو رمز Variational Autoencoder.

مهمتنا هي بناء نموذج عام وتدريبه باستخدام طريقة الاحتمالية القصوى. سيكون للنموذج النموذج التالي:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

حيث $$$ف (س)$ هي كثافة الاحتمال للعينات المولدة ، $$$z$ - المتغيرات الكامنة ، $$$ف (ض)$ - كثافة الاحتمال لمتغير كامن (غالبًا ما يكون أحد المتغيرات البسيطة - على سبيل المثال ، توزيع غاوسي متعدد الأبعاد مع توقع صفر وتشتت الوحدة - بشكل عام ، شيء يمكننا أخذ عينات منه بسهولة) ، $$$q_ \ theta (x | z)$ - يتم تحديد كثافة العينة الشرطية لقيمة معينة من المتغيرات الكامنة ، في وحدة الترميز التلقائي التباين ، يتم تحديد مقياس غاوسي مع توقع حصيرة وتشتت اعتمادا على z.

لماذا قد نحتاج إلى تمثيل كثافة البيانات بهذه الطريقة المعقدة؟ الجواب بسيط - البيانات لها وظيفة كثافة معقدة للغاية ولا يمكننا ببساطة بناء نموذج من هذه الكثافة بشكل مباشر. نأمل أن يتم تقريب هذه الكثافة المعقدة جيدًا باستخدام كثافتين أبسط. $$$ف (ض)$ و $$$q_ \ theta (x | z)$ .

نريد تعظيم الوظيفة التالية:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

حيث $$$p (x)$ - كثافة احتمال البيانات. المشكلة الرئيسية هي أن الكثافة $$$ف (س)$ (مع نماذج مرنة بما فيه الكفاية) لا يمكن تقديم التحليل ، وبالتالي تدريب النموذج.

نستخدم صيغة بايز ونعيد كتابة وظيفتنا على النحو التالي:

$$

$$I = \ int {p (x) log (\ frac {q (z) q (x | z)} {q (z | x)}) dx}$$

لسوء الحظ، $$$q (z / x)$ من الصعب حساب كل شيء أيضًا (من المستحيل أخذ التحليل المتكامل). لكن أولاً ، نلاحظ أن التعبير تحت اللوغاريتم لا يعتمد على z ، لذلك يمكننا أخذ التوقع الرياضي من اللوغاريتم في z لأي توزيع وهذا لن يغير قيمة الوظيفة ويتضاعف ويقسم اللوغاريتم في نفس التوزيع (رسميًا لدينا شرط واحد فقط - هذا التوزيع لا ينبغي أن تختفي في أي مكان). نتيجة لذلك ، نحصل على:

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + + \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {\ phi (z | x)} {q (z | x)})}}$$

لاحظ أنه ، أولاً ، المصطلح الثاني هو اختلاف KL (مما يعني أنه إيجابي دائمًا):

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + + \ int {p (x) KL [\ phi (z | x) || q (z | x))] dx}$$

وثانيا $$$I$ لا يعتمد على $$$q (z | x)$ ليس من $$$\ phi (z | x)$ . يتبع ذلك ،

$$

$$I> = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} = VLB$$

حيث $$ - الحد الأدنى للتغيير (الحد الأدنى المتغير) ويصل إلى الحد الأقصى عندما $$$KL [\ phi (z | x) || q (z | x))] = 0$ - أي التوزيعات هي نفسها.

الإيجابية والمساواة إلى الصفر إذا وفقط إذا كانت التوزيعات تتزامن مع اختلافات KL ، تم إثباتها على وجه الدقة بطرق مختلفة - وبالتالي الحدود الاسمية للتغير.

أريد أن أشير إلى أن استخدام الحد الأدنى التباين يعطي العديد من المزايا. أولاً ، يتيح لنا الفرصة لتحسين وظيفة الخسارة من خلال أساليب التدرج (حاول القيام بذلك عندما لا يتم أخذ التكامل بشكل تحليلي) وثانياً ، تقارب التوزيع العكسي $$$q (z | x)$ توزيع $$$\ phi (z | x)$ - وهذا يعني أنه لا يمكننا فقط أخذ عينات من البيانات ، ولكن أيضًا أخذ عينات من المتغيرات الكامنة. لسوء الحظ ، فإن العيب الرئيسي هو عندما يكون نموذج التوزيع العكسي غير مرن ، أي عندما تكون الأسرة $$$\ phi (z | x)$ لا يحتوي $$$q (z | x)$ - ستكون الباقي إيجابية ومتساوية:

$$

$$\ delta = \ int {p (x) \ underset {\ phi (z | x)} {min} (KL [\ phi (z | x) || q (z | x)]) dx}$$

وهذا يعني أن الحد الأقصى للحد الأدنى ووظائف الخسارة على الأرجح لا يتزامنان. بالمناسبة ، يولد المشفر التلقائي المتغير المستخدم في إنشاء الصور ضبابية للغاية ، وأعتقد أن السبب في ذلك هو اختيار عائلة فقيرة للغاية $$$\ phi (z | x)$ .

مثال على الخلاصة غير الجيدة

الآن سننظر في مثال حيث ، من ناحية ، يحتوي الحد السفلي على كل الخصائص الجيدة (مع نموذج مرن بما فيه الكفاية ، والباقي سيكون صفرا) ، ولكن بدوره لا يعطي أي ميزة على استخدام وظيفة الخسارة الأصلية. أعتقد أن هذا المثال كاشٍ للغاية وإذا لم تقم بإجراء تحليل نظري ، فيمكنك قضاء الكثير من الوقت في محاولة لتدريب نماذج لا معنى لها. بدلاً من ذلك ، تكون النماذج منطقية ، ولكن إذا استطعنا تدريب مثل هذا النموذج ، فسيكون من السهل اختياره $$$ف (س)$ من نفس العائلة واستخدم مبدأ الاحتمال الأقصى مباشرة.

لذلك ، سوف نأخذ بعين الاعتبار نفس النموذج التوليفي بالضبط كما هو الحال في برنامج التشفير التلقائي المتغير:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

سنقوم بالتدريب باستخدام نفس طريقة الاحتمالية القصوى:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

ما زلنا نأمل ذلك $$$q (x | z)$ سيكون "أسهل" من $$$ف (س)$ .
الآن فقط سوف نكتب $$$I$ مختلف قليلا:

$$

$$I = \ int {p (x) log (\ int {q (z) q_ \ theta (x | z) dz}) dx}$$

باستخدام صيغة جنسن ، نحصل على:

$$

$$I> = \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz} = VLB$$

في هذه اللحظة بالتحديد ، يستجيب معظم الأشخاص دون التفكير في أن هذا هو في الحقيقة الحد الأدنى ويمكنك تدريب النموذج. هذا صحيح ، لكن دعونا ننظر إلى التناقض:

$$

$$\ delta = \ int {p (x) log (q (x)) dx} - \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz}$$

حيث (من خلال تطبيق صيغة بايز مرتين):

$$

$$\ delta = \ int {p (x) q (z) log (\ frac {q (x)} {q (x | z)}) dxdz} = \ int {p (x) q (z) log ( \ frac {q (z)} {q (z | x)}) dxdz}$$

من السهل أن نرى ما يلي:

$$

$$\ delta = \ int {p (x) KL [q (z) || q (z | x)] dx}$$

دعونا نرى ما يحدث إذا قمنا بزيادة الحد الأدنى - ستنخفض النسبة المتبقية. مع نموذج مرن إلى حد ما:

$$

$$KL [q (z) || q (z | x)] \ rightarrow0$$

يبدو أن كل شيء على ما يرام - الحد الأدنى لديه صفر المتبقية المتبقية ونموذج مرن إلى حد ما $$$q (x | z)$ كل شيء يجب أن تعمل. نعم ، هذا صحيح ، يمكن للقراء المهتمين فقط أن يلاحظوا أن الصفر المتبقي يتحقق عندما $$$x$ و $$$z$ متغيرات عشوائية مستقلة !!! ولنتيجة جيدة ، "تعقيد" التوزيع $$$q (x | z)$ يجب أن لا يقل عن $$$ف (س)$ . أي أن الحدود الدنيا لا تمنحنا أي مزايا.

النتائج

يمثل الحد الأدنى من التباين أداة رياضية ممتازة تتيح لك تحسين وظائف "مزعجة" للتعلم تقريبًا. ولكن مثل أي أداة أخرى ، يجب أن تفهم جيدًا مزاياها وعيوبها وأن تستخدمها أيضًا بعناية فائقة. لقد اعتبرنا مثالًا جيدًا للغاية - تشفير تلقائي متنوع ، وكذلك مثال للحد الأدنى غير الجيد للغاية ، بينما يصعب رؤية مشاكل هذا الحد السفلي دون تحليل رياضي مفصل.

آمل أن تكون مفيدة ومثيرة للاهتمام على الأقل.