صيغة لحساب الأعداد الأولية وتحسين المقسومات القوة الغاشمة

تحية! قررت في وقت فراغي أن أبحث عن مشكلة إيجاد الأعداد الأولية. الموضوع واسع وممتع. أريد أن أشارك زوجين من الأفكار التي تتبادر إلى الذهن. لم يكشف البحث على الإنترنت عن ذلك ، مشيرا إلى أصالتها.

أولاً ، لم أجد أبدًا صيغة رياضية لحساب الأعداد الأولية بالترتيب. ولكن بعد كل شيء ، إذا كان هناك خوارزميات ، فمن الممكن بالتأكيد إنشاء صيغ باستخدام وظائف منطقية أو عوامل تشغيل. أعطي أدناه الصيغة الأكثر إيجازًا التي تحولت.

لبعض تسلسل الأرقام $$$(x_ {m}) = {x_ {1} ، x_ {2} ، x_ {3} ، ... x_ {max}}$ نقدم لك عامل اكتشاف الرقم الأول الذي يساوي:

$$

$$\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ start {matrix} m \ \ mathbf {if} \ \ موجود \ m: \ forall \، k <m \ x_ {k } \ neq a \ \ mathbf {and} \ x_ {m} = a \\ 0 \ \ mathbf {وإلا} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ نهاية {matrix} \ right.$$

يمكن حساب جميع الأعداد الأولية ، بدءًا من 5 ، بالصيغة:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i) \، mod \، P_ {j + 1}))، \ \ \ \ forall \، n \ geqslant 3 \\ \ forall \، i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ،، \ \ 2 \ leqslant \ alpha \ leqslant n-1؛ \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1 دولا$$

عامل $$$\ mathbf {Dt_ {0} ^ {j}}$ يتكرر أكثر $$$j$ ما تبقى من تقسيم كل رقم مرشح على البساطة مع $$$i$ عدد ال $$$(P_ {n-1} + 2i)$ إلى الأعداد الأولية الموجودة بالفعل في نطاق يصل إلى $$$P_ {j_ {max} +1}$ . يتم تحديد أرقام المرشحين بالترتيب من مجموعة الأرقام الفردية أكبر من الرقم الأولي السابق $$$P_ {n-1}$ . $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ هي وظيفة pi تبين عدد الأعداد الأولية $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .
عامل $$$\ mathbf {Dt_ {0} ^ {i}}$ يتكرر أكثر $$$i$ قيم خرج المشغل $$$\ mathbf {Dt_ {0} ^ {j}}$ حتى يتم العثور على 0. نظرًا لأن سلسلة الأعداد الأولية لا نهائية ، فسيحدث ذلك عاجلاً أم آجلاً. عند الخروج من المشغل $$$\ mathbf {Dt_ {0} ^ {i}}$ لذلك سيكون هناك دائما بعض الأرقام $$$i$ . الحد الأدنى $$$i_ {max}$ يتم تحديده بواسطة الحد الأقصى للفرق بين الأعداد الأولية المجاورة الأصغر من الأولى. الزيادة في هذا الاختلاف تحدث لوغاريتميا. يوضح الرسم البياني أدناه اعتماد الحد الأقصى ومتوسط ​​النمو $$$\ Delta P _ {\ alpha}$ من ن لأول 100،000 الأعداد الأولية. تم أخذ عينات من القيمة القصوى ومتوسطها لكل ألف رقم.
أقصى زيادة في اختلاف الأعداد الأولية $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ إلى القيمة القصوى السابقة $$$كحد أقصى (\ Delta P _ {\ alpha})$ يساوي 20 (لفرق الأعداد الأولية 31397-31469 = 72 بالنسبة للفرق 25523-25471 = 52). هو في المنطقة حيث مشتق لوغاريتم المغلف $$$\ Delta P _ {\ alpha}$ لا تزال كبيرة بما فيه الكفاية ، والأعداد الأولية لم تعد صغيرة جدا. بناء على هذه القيمة ، شرط ل $$$i_ {max}$ . جدول المواعيد $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ لأول 50،000 الأعداد الأولية الواردة أدناه. تم حساب القيم لكل ألف.
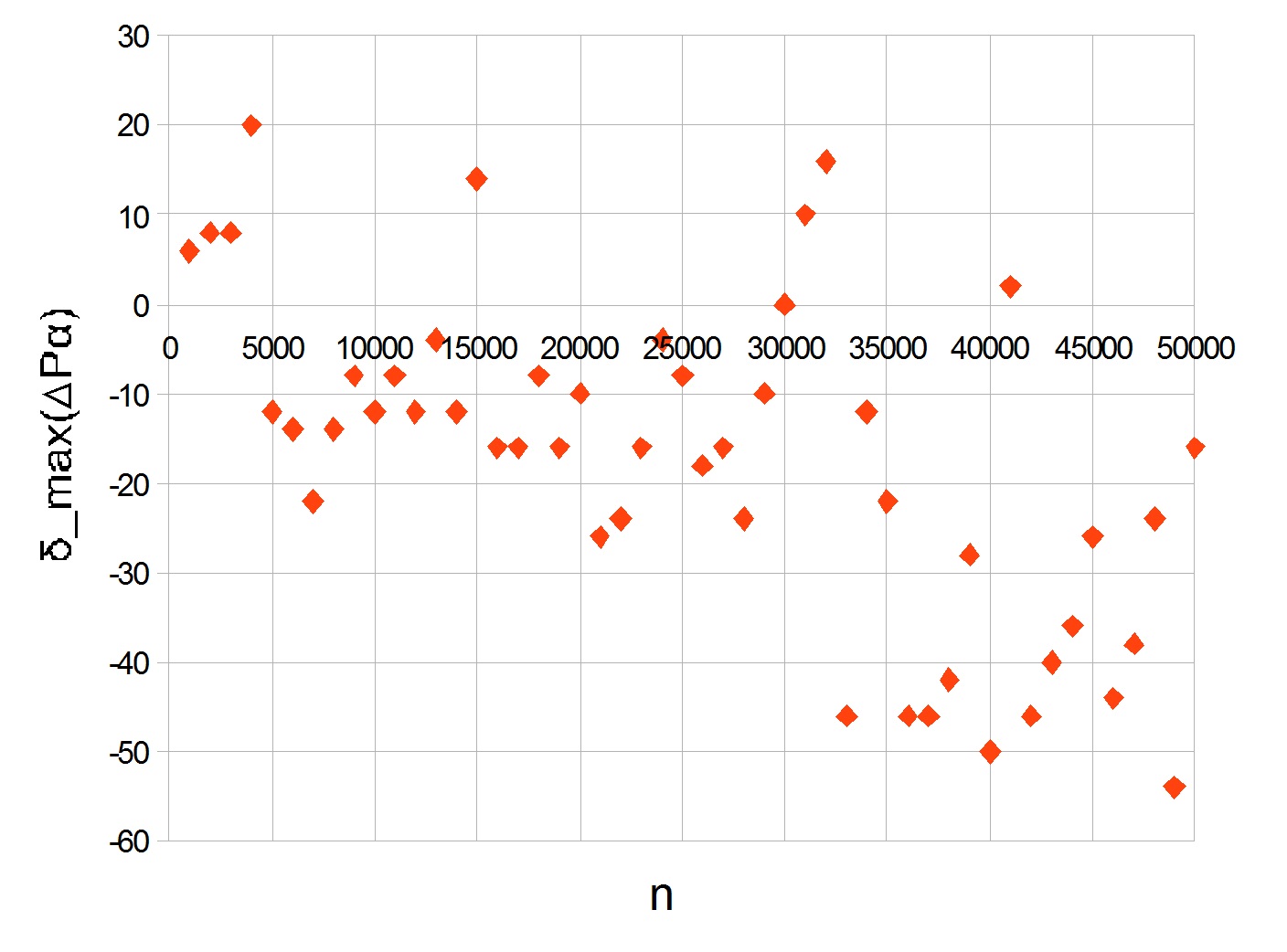
ذروة مرئية في 20. مع زيادة ن ، يذهب الرسم البياني إلى ناقص ، مما يدل على انخفاض في معدل نمو الأعداد الأولية الكبيرة.

الاعتبار الثاني هو تحسين حساب سلسلة من الأعداد الأولية.
الخوارزمية المنصوص عليها في الصيغة أعلاه هي طريقة محسنة لتعداد المقسومات. التحسينات هي استبعاد الأرقام الزوجية من الاعتبار والتحقق من قابلية القسمة على الأعداد الأولية الأصغر من المربع. جذور أعداد المرشحين. الجزء الأكثر صعوبة من الخوارزمية هو حساب مجموعة من وظائف وزارة الدفاع المتبقية. يمكن تقليل التعقيد عن طريق تحسين هذه الوظيفة. ومع ذلك ، هناك طريقة أكثر فعالية. سمح $$$(r_ {j + 1} ^ {n-1}) = {r_ {2} ، r_ {3} ، ... r _ {\ pi (\ sqrt {P_ {n-1}})}}}$ هو سلسلة من المخلفات من قسمة آخر رقم تم العثور عليه في الأعداد الأولية من 3 إلى جذره. سنجعل تسلسل النموذج

$$

$$(r_ {i، j + 1} ^ {n}) = {(r_ {2} + 2i) \، mod \، P_2، (r_ {3} + 2i) \، mod \، P_3، ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \، mod \، P _ {\ pi (\ sqrt {P_ {n-1}})}، (P_ {n -1} + 2i) \، mod \، P _ {\ \ pi (\ sqrt {P_ {n-1} + 2i})}}$$

من أجل البدء من $$$i = 1$ . يتم احتساب المصطلح الأخير إذا $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . عندما في بعض خطوة من الحساب الباقي $$$r_ {i، j + 1} ^ {n}$ يصبح يساوي 0 ، انتقل إلى التسلسل التالي. يتم ذلك حتى يتم العثور علي ، حيث تكون جميع المخلفات غير صفرية. هذا يعني إيجاد العدد الأولي التالي. تسلسل $$$(r_ {j + 1} ^ {n})$ يجب حفظه حتى يتم العثور على الرقم الأولي التالي. يتم تحويل الصيغة المتكررة لحساب الأعداد الأولية بهذه الطريقة إلى:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i، j + 1} ^ { n})) ، \ \ \ \ forall \ ، n \ geqslant 3$$

في الخوارزمية المقدمة ، يتم تسهيل عملية التشغيل: divisible by $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ مرات أكثر المقسمات. الاستثناءات الوحيدة هي حدوث المقسومات البسيطة الجديدة. في ذاكرة الكمبيوتر ، عند تنفيذ الخوارزمية ، من الضروري تخزين مجموعة من الأعداد الأولية إلى جذر المتطلب ، وكذلك مجموعة متغيرة من البقايا. قد يكون تعقيد الخوارزمية بالمعنى العام (مقدار العمل) أقل من الطرق الأخرى المعروفة. أكثر العمليات تعقيدًا فيها هي استخراج الجذر التربيعي وحساب المخلفات والضرب. يمكن استخراج الجذر إلى أقرب عدد صحيح. للحصول على البقايا ، يمكنك استخدام خوارزمية فعالة تستند إلى قاعدة عامة للقسمة. يتم استخدام الضرب فقط من قبل 2 أعداد صغيرة نسبيا ط . يمكن تقليل التعقيد الزمني للخوارزمية عن طريق توزيع العمل وفقًا لقيم i . يجب أن يعمل المنخل المقسم الذي تم الحصول عليه بهذه الطريقة بشكل أسرع على أجهزة الكمبيوتر متعددة الخيوط. ومع ذلك ، فإن العمل المنجز سيكون أكبر بسبب الزيادة في الأرباح. يمكنك أيضًا تثبيت "تثبيت" العجلة على الخوارزمية. مع الحجم الأمثل للعجلات ، يمكن أن يقلل هذا من التعقيد في نطاق معين من n - حتى يبطئ الجهاز "wilds".

ربما شخص ما سوف يأتي في متناول يدي أفكاري.