أشجار البحث الثنائية هي بنية بيانات لتخزين العناصر ذات قدرات البحث السريع. الفكرة بسيطة ومبدعة: "أقل اليسار ، وأكثر هو الصحيح". هذا هو المكان الذي تنتهي فيه البساطة وتبدأ الأسئلة المعقدة الخاصة بموازنة شجرة بحيث لا تتحول إلى فرع طويل.

في هذه المقالة ، سنقدم تعريفًا ، وسرد قواعد وضع العناصر في شجرة حمراء سوداء ، والنظر في خوارزمية موازنة ، ودمج ما قيل في مثال. ندرس هذا الموضوع بمزيد من التفاصيل ، وكذلك الأنواع الأخرى من أشجار البحث الثنائية في الدورة التدريبية "الخوارزميات للمطورين" . الشجرة الحمراء السوداء
الشجرة الحمراء السوداء هي
شجرة بحث ثنائية ذاتية التوازن تضمن نمو لوغاريتمي لارتفاع الشجرة من عدد العقد والتنفيذ السريع للعمليات الأساسية لشجرة البحث: إضافة العقدة وحذفها والبحث عنها.
الشجرة الحمراء السوداء غير متوازنة تمامًا ، في بعض الأماكن يمكن أن يتفاوت ارتفاعها مرتين تقريبًا. لا يؤثر هذا الافتراض بشكل غير مقارب على سرعة البحث عن العناصر ، ولكنه يسرع بشكل كبير من وضع العناصر الجديدة ، لأنك لا تحتاج إلى "هز" الشجرة في كل مرة تضيف فيها عناصر ، أحيانًا يكفي فقط إضافة عنصر أحمر دون لمس العناصر الأخرى ودون تغيير "الارتفاع الأسود" .
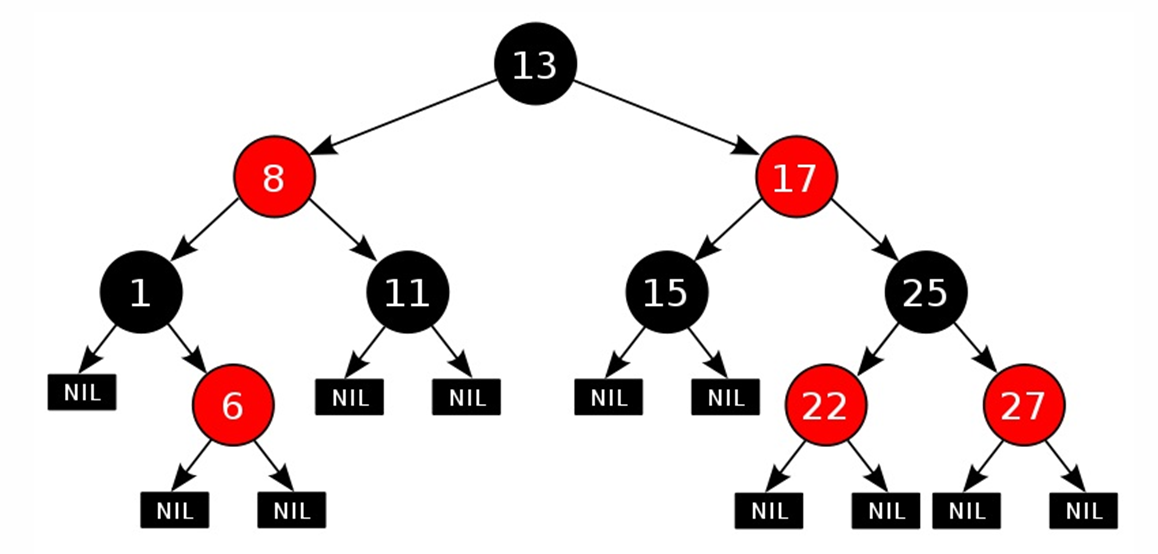
قواعد لوضع العناصر في شجرة حمراء سوداء
- كل عقدة إما حمراء أو سوداء ؛ أوراق NIL دائماً سوداء.
- جذر الشجرة دائما أسود
- كلا أحفاد كل عقدة حمراء سوداء
- يحتوي المسار لأسفل من أي عقدة إلى أي ورقة نزول على نفس عدد العقد السوداء.
عند إدراج عنصر جديد ، يتم تعيين لون أحمر له. لتحقيق أول قاعدتين ، ما عليك سوى إعادة رسم القمم الجديدة بالألوان المرغوبة.
النظر في قواعد التوازن لتنفيذ 3 و 4 نقاط.
في كل شكل ، يُفترض أننا قمنا بالفعل بإضافة عنصر X ينتهك القاعدة 3 ، ونحن بحاجة إلى تغيير بنية الشجرة بحيث يتم تنفيذ القاعدة 3 ، وعدم انتهاك 4.
أسطورة القمم:
- X - عنصر إضافي ينتهك 3 فقرة من القواعد.
- ف - البند العاشر
- ز- جد العنصر X ، والد العنصر P
- U هو عم العنصر X ، شقيق العنصر P ، الابن الثاني للعنصر G.
الحالة الأولى - العم الأحمر
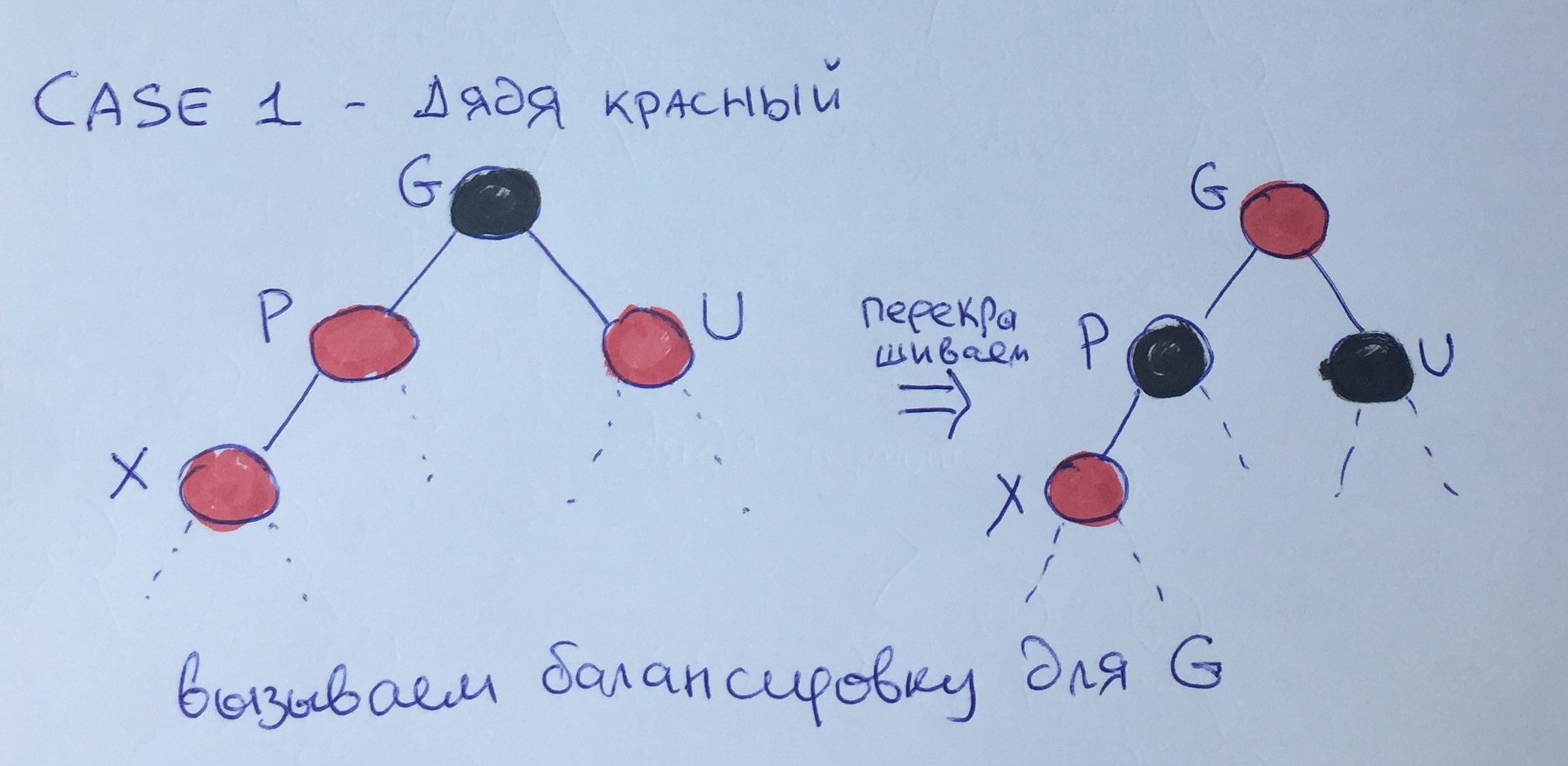
إذا كان كل من الأب والعم حمراء ، فيمكننا "خفض" اللون الأسود من مستوى الجد إلى مستوى الأب وإعادة رسم العقد ، كما هو موضح في الشكل. في هذه الحالة ، سيبقى "الارتفاع الأسود" على حاله ، ومع ذلك ، فمن الممكن انتهاك القاعدة 3 للعنصر G ، لذلك ، من الضروري استدعاء مزيد من الموازنة بشكل متكرر لهذه العقدة.
الحالة الثانية - عم أسود - أبي وجده في اتجاهات مختلفة.
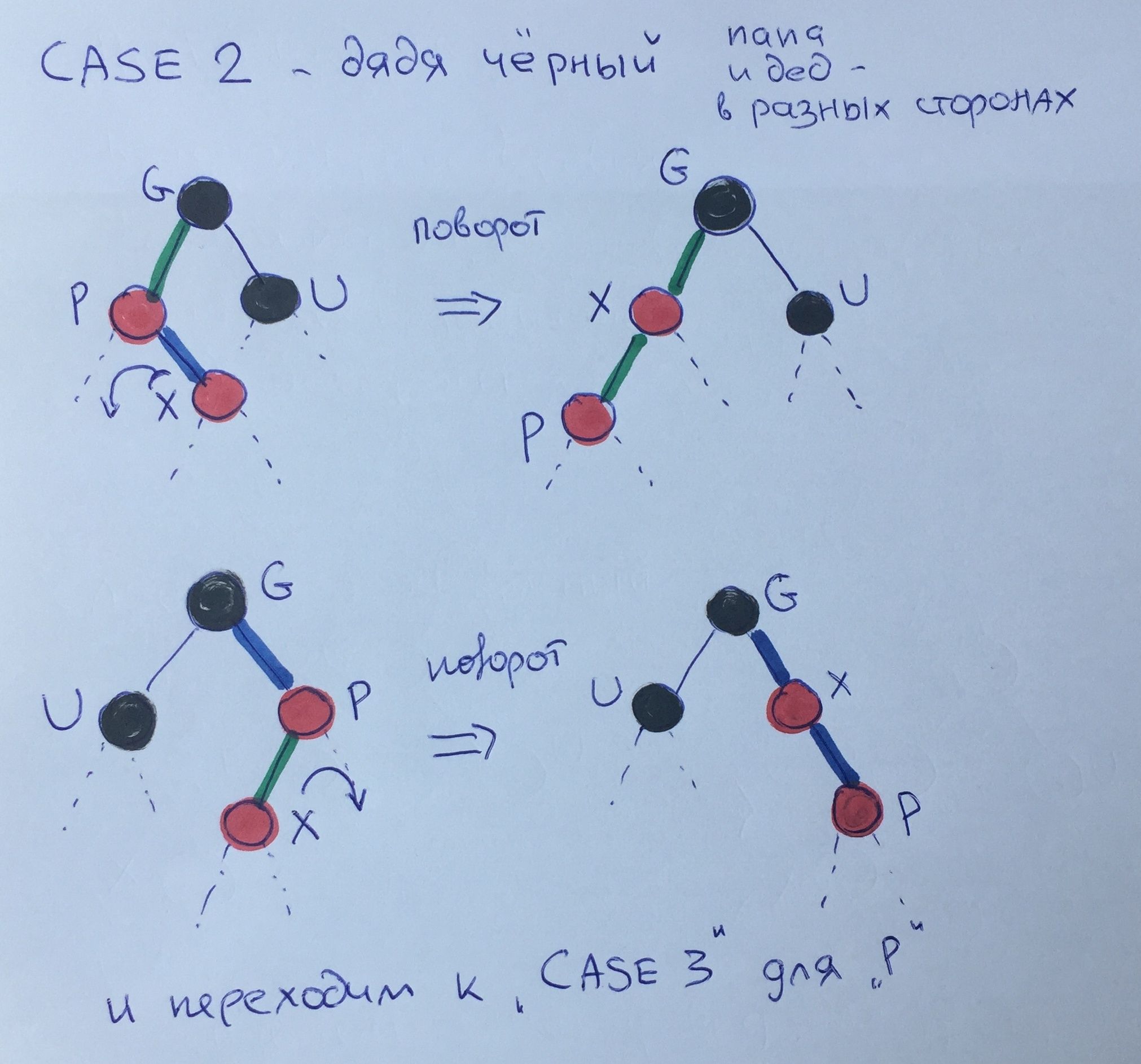
يجب إحضار هذا الهيكل إلى الحالة الثالثة ، عندما يذهب الأب وجده في نفس الاتجاه. للقيام بذلك ، تحتاج إلى جعل منعطفًا صغيرًا من الابن X إلى والده (لا يتم اعتبار قواعد المنعطفات في هذه المقالة) واستدعاء 3 حالات للعنصر R.
الحالة الثالثة - العم الأسود - أبي وجده على نفس الجانب
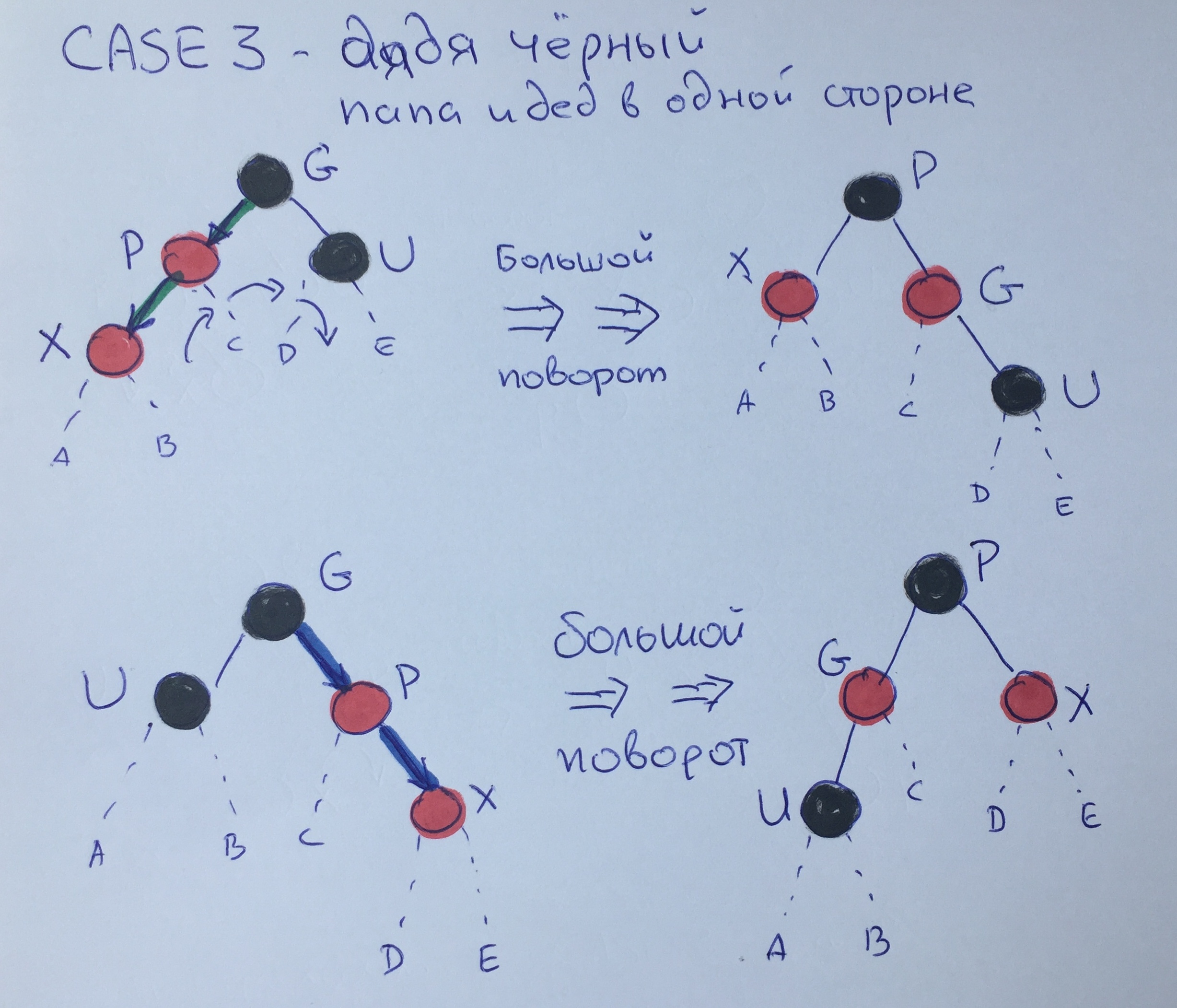
في هذه الحالة ، يمكننا بالفعل تحويل كبير من الأب من خلال الجد إلى العم الأسود وإعادة رسم P باللون الأسود و G باللون الأحمر. نتيجة لهذا التناوب ، سوف تكون راضية 3-القاعدة.
تأكد من أن القاعدة الرابعة راضية أيضًا. افترض أنه قبل المنعطف الكبير ، كان الارتفاع الأسود للعنصر G هو N + 2. سيكون ارتفاع العناصر "المعلقة" كما يلي:
A = N + 1 ،
B = N + 1 ،
C = N + 1 ،
D = N
E = N.
انظر لنفسك أنه بعد قلب القاعدة الأربع ، صحيح بالنسبة لجميع العناصر.
مثال ملموس
سننظر الآن في عملية تشكيل شجرة حمراء سوداء مع إدراج متتالي للعناصر 1 و 2 و 3 و 4 و 5 و 6.
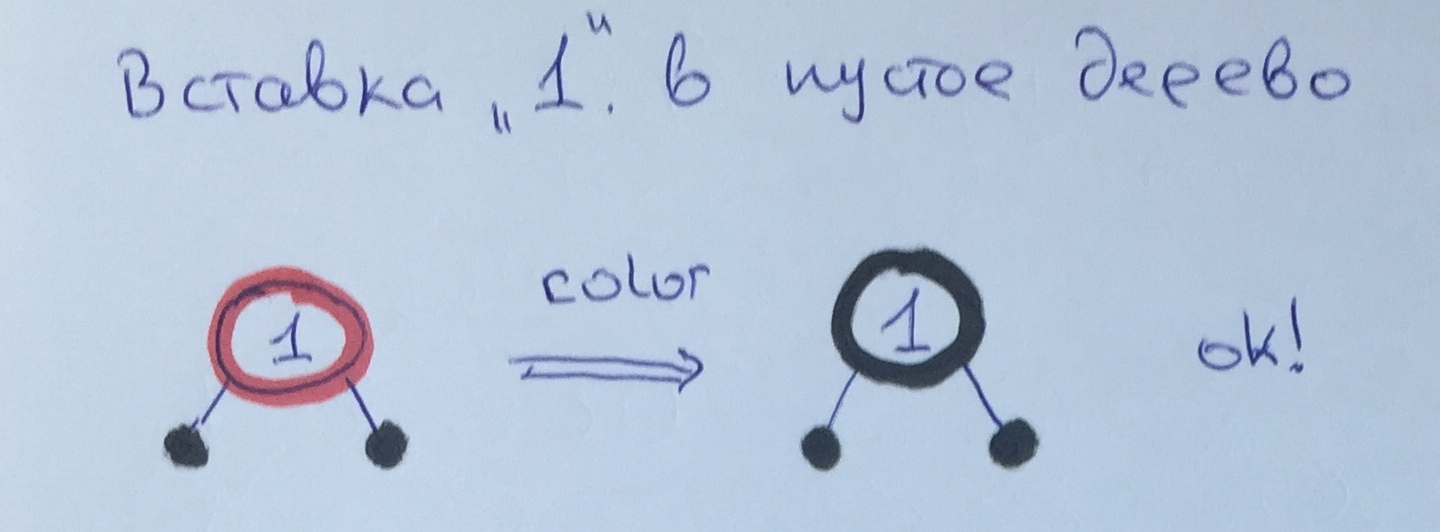
بما أن العنصر 1 هو الجذر ، فنحن ببساطة نعيد طلاءه للوفاء بالقاعدة 1.
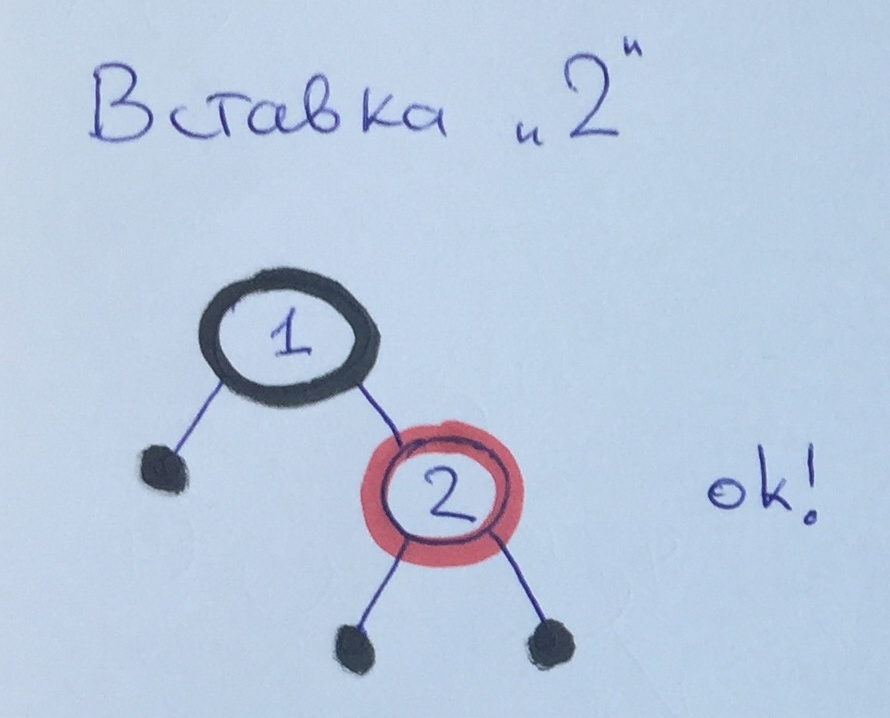
بعد إضافة العنصر 2 ، يتم تنفيذ جميع القواعد.
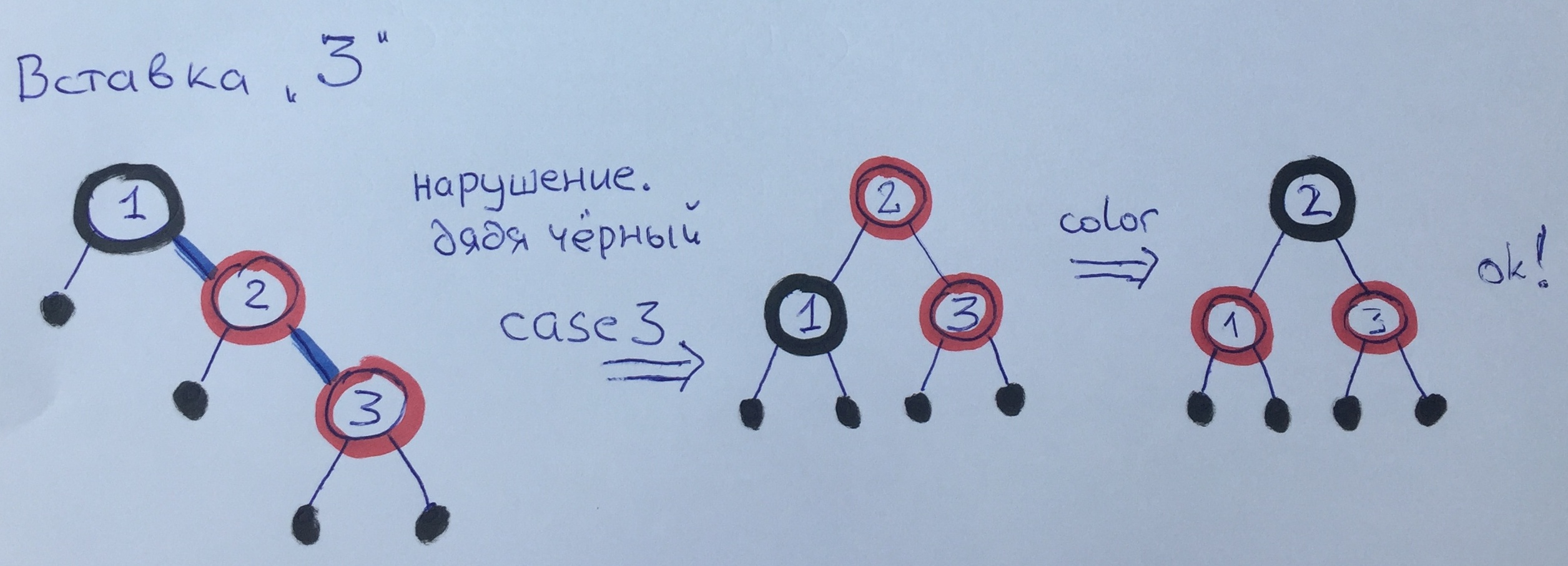
عند إضافة العنصر 3 ، انتهكنا القاعدة 3. نظرًا لأن لدينا عمًا أسود ، وجدًا وأبًا من جهة ، نستخدم الحالة الثالثة - ننتقل ونعيد الطلاء.
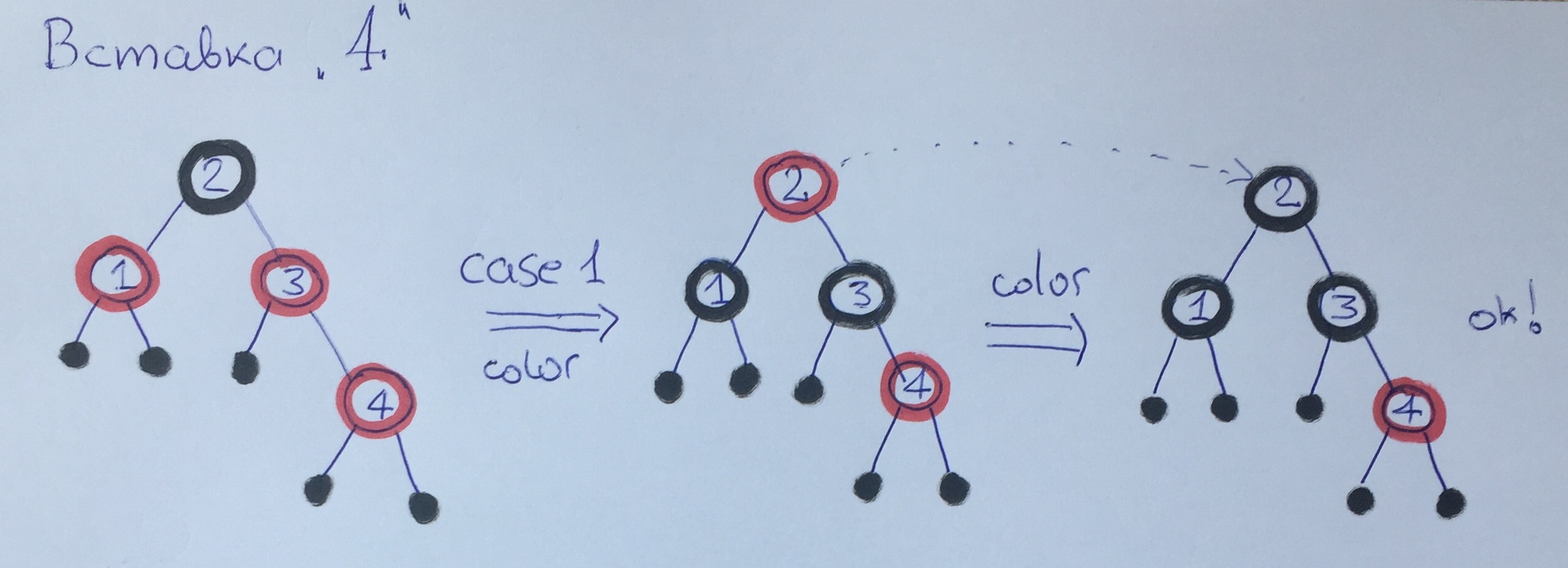
عند إضافة العنصر 4 ، انتهكنا مرة أخرى القاعدة 3. هذه المرة يكون عمنا أحمر ، لذلك نطبق الحالة الأولى مع إعادة الطلاء - الارتفاع الأسود للشجرة سيزداد بمقدار 1. يرجى ملاحظة. إطلاق خوارزمية الموازنة بشكل إضافي للجد - العنصر 2 ، والذي ، مثل الجذر ، يتم طلاؤه ببساطة باللون الأسود.
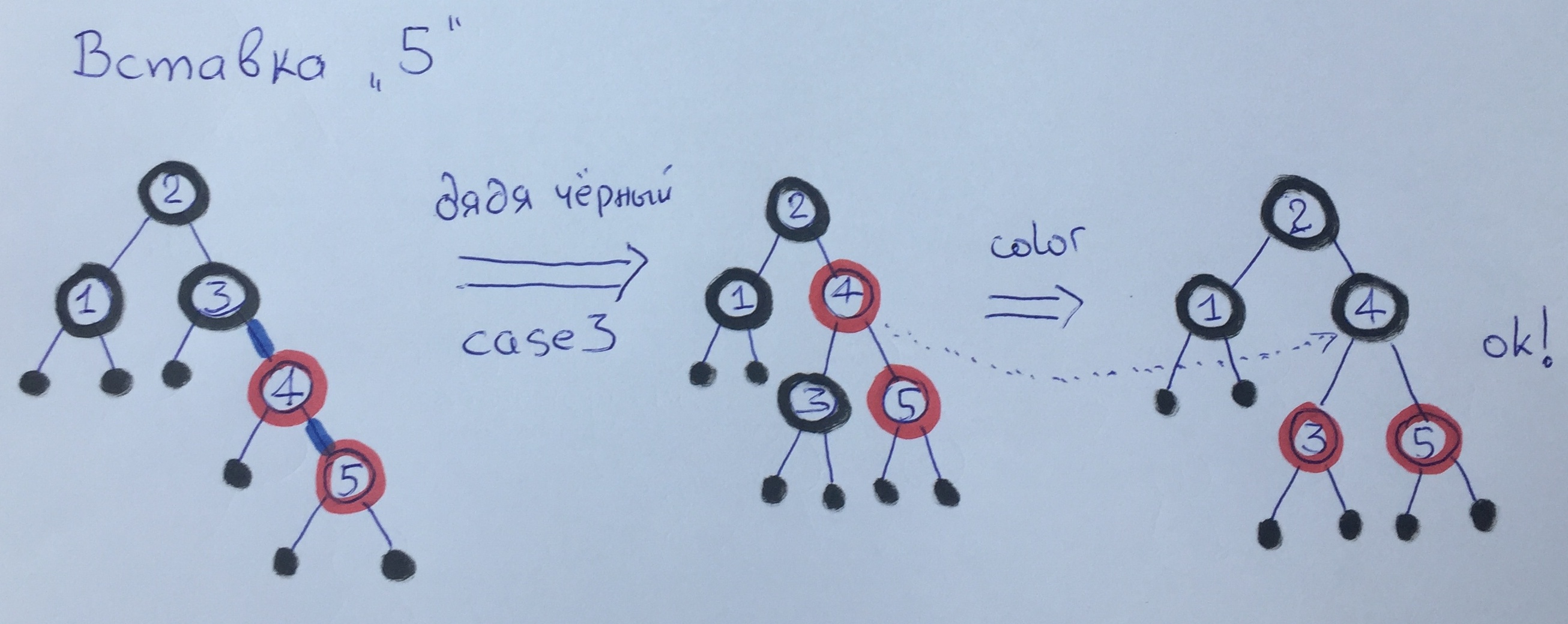
عند إدخال العنصر 5 ، نقوم مرة أخرى بتطبيق الحالة الثلاث - ننتقل إلى حد كبير ونعيد رسم القمم. لاحظ أن الارتفاع الأسود لم يتغير.
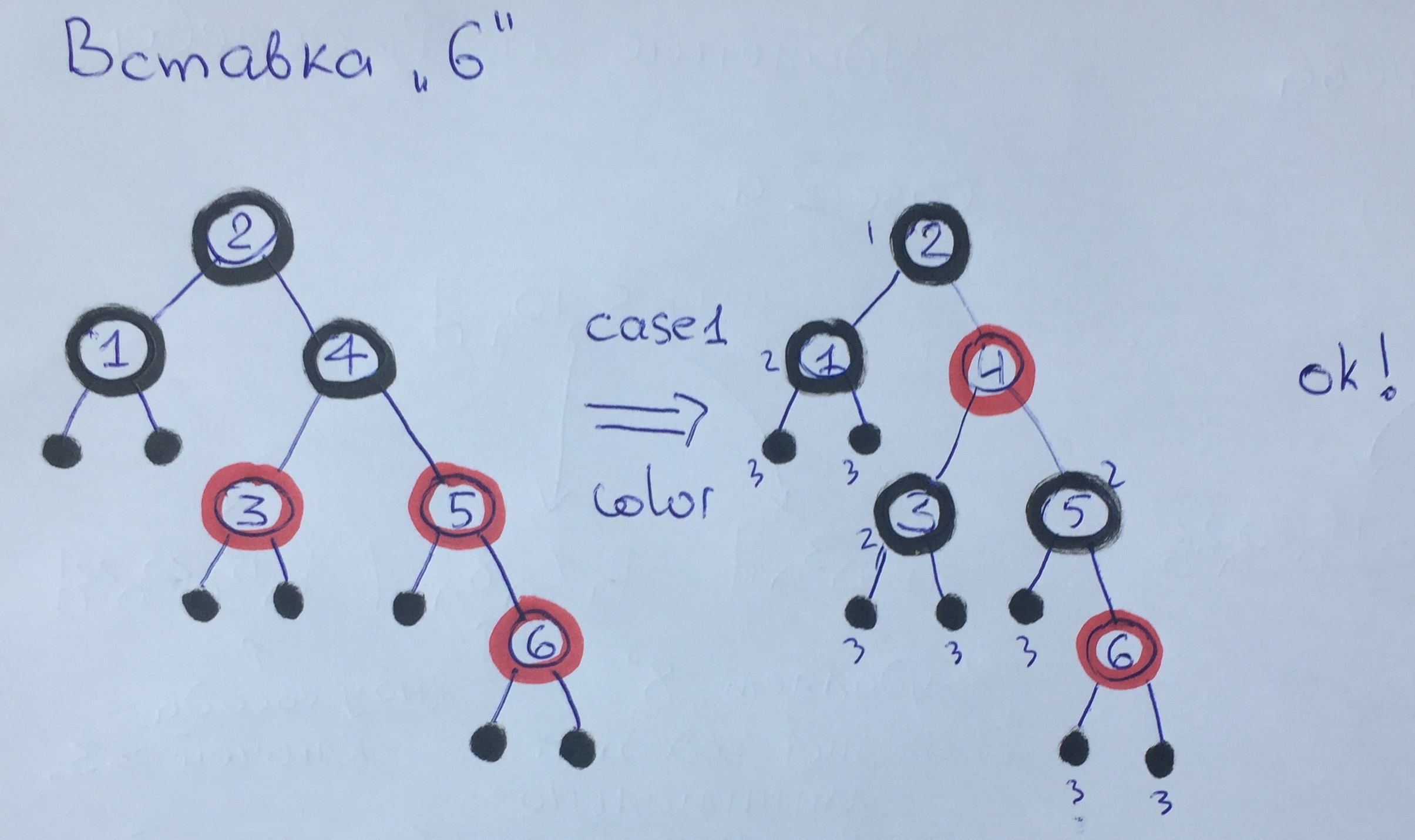
عند إضافة العنصر 6 ، انتهكنا مرة أخرى القاعدة 3. منذ عمنا أحمر ، نطبق الحالة الأولى مع إعادة طلاء ، لم يتغير الارتفاع الأسود. لم يغير استدعاء الموازنة لـ 4 عناصر أي شيء في الشجرة ، لأن هذا العنصر لا ينتهك القواعد.
لذلك ، تعرفنا على قضايا موازنة الشجرة الحمراء السوداء ، بمزيد من التفصيل ومع أمثلة من الخوارزميات لهذا الموضوع ، بالإضافة إلى أنواع أخرى من أشجار البحث الثنائية الأخرى ، فإننا نعتبرها في الدورة التدريبية
"الخوارزميات للمطورين" .