نزول التدرج العشوائي (SGD) لوظيفة الخسارة اللوغاريتمية (LogLoss) في مشكلة التصنيف الثنائي

الجزء السابق (حول الانحدار الخطي ونزول التدرج وكيف يعمل كل شيء) - habr.com/ar/post/471458

في هذه المقالة ، سأعرض حلاً لمشكلة التصنيف أولاً ، كما يقولون ، "الأقلام" ، بدون مكتبات تابعة لجهة أخرى لـ SGD و LogLoss وحساب التدرجات ، ثم باستخدام مكتبة PyTorch.

الهدف: لاثنين من الميزات الفئوية التي تصف الصفار والتماثل ، حدد الفئة (تفاحة أو كمثرى) التي ينتمي إليها الكائن (علم النموذج لتصنيف الكائنات).

للبدء ، قم بتحميل مجموعة البيانات الخاصة بنا:

import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10) 

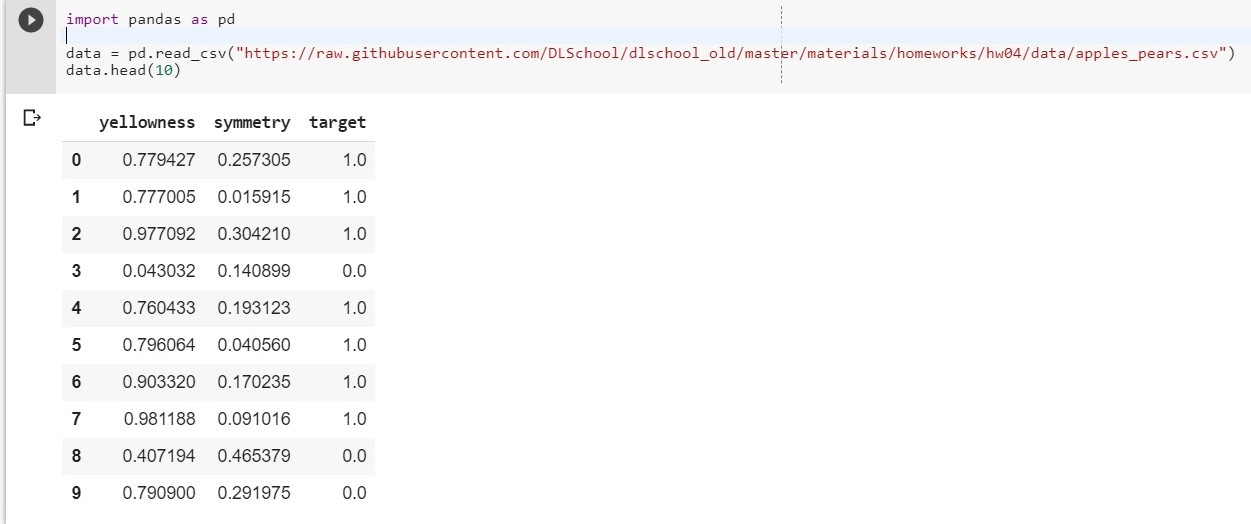
اسمحوا: X1 - اصفرار ، X2 - التماثل ، ص = targer

نحن نؤلف الوظيفة y = w1 * x1 + w2 * x2 + w0
(سيتم اعتبار w0 هو الانحياز (eng. - bias))

تم الآن تقليل مهمتنا إلى إيجاد الأوزان w1 و w2 و w0 ، والتي تصف بدقة أكثر اعتماد y على x1 و x2.

نحن نستخدم وظيفة فقدان لوغاريتمي:



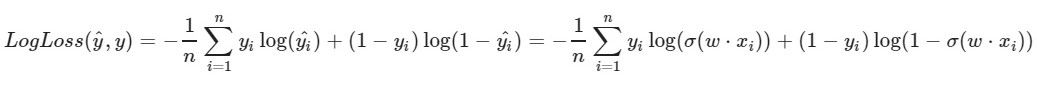
المعلمة اليسرى للدالة هي التنبؤ بالأوزان الحالية w1 و w2 و w0

المعلمة الصحيحة للدالة هي القيمة الصحيحة (الفئة هي 0 أو 1)

x (x) هي وظيفة التنشيط السيني لـ x

log (x) - اللوغاريتم الطبيعي لـ x

من الواضح أنه كلما كانت قيمة دالة الخسارة أصغر ، كان اختيار الأوزان w1 و w2 و w0 أفضل. للقيام بذلك ، اختر النسب التدرج العشوائي .

لاحظت أن صيغة LogLoss ستلقي نظرة مختلفة في ضوء حقيقة أننا في SGD نختار عنصرًا واحدًا وليس تحديدًا كاملاً (أو نموذج فرعي ، كما في حالة نزول تدرج الدُفعات المصغرة):


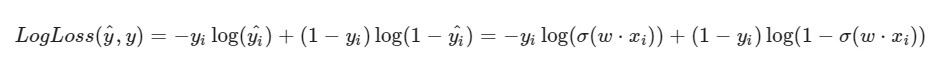تقدم الحل:

يتم إعطاء الأوزان الأولية w1 و w2 و w0 قيمًا عشوائية

نأخذ كائنًا i معينًا من مجموعة البيانات الخاصة بنا (على سبيل المثال ، عشوائيًا) ، ونحسب LogLoss له (باستخدام w1 و w2 و w0 ، حيث قمنا بتعيين قيم عشوائية في البداية) ، ثم نحسب المشتقات الجزئية لكل من الأوزان w1 و w2 و w0 ، ثم تحديث كل من الأوزان.

القليل من التحضير:

 import pandas as pd import numpy as np X = data.iloc[:,:2].values #  - y = data['target'].values.reshape((-1, 1)) #  (    ) x1 = X[:, 0] x2 = X[:, 1] def sigmoid(x): return 1 / (1 + np.exp(-x)) 

التنفيذ:

 import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1) print(w1, w2, w0) # form range 0..999 idx = np.arange(1000) # random shuffling np.random.shuffle(idx) x1, x2, y = x1[idx], x2[idx], y[idx] # learning rate lr = 0.001 # number of epochs n_epochs = 10000 for epoch in range(n_epochs): i = random.randint(0, 999) yhat = w1 * x1[i] + w2 * x2[i] + w0 w1_grad = -((y[i] - sigmoid(yhat)) * x1[i]) w2_grad = -((y[i] - sigmoid(yhat)) * x2[i]) w0_grad = -(y[i] - sigmoid(yhat)) w1 -= lr * w1_grad w2 -= lr * w2_grad w0 -= lr * w0_grad print(w1, w2, w0) 

[0.49671415] [-1.1382643] [0.64768854]
[0.87991625] [-1.14098372] [0.22355905]

* _grad هو مشتق من الوزن المقابل. سأكتب المعادلة العامة:



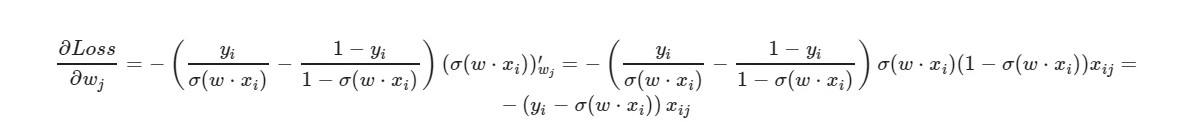
للمصطلح الحر w0 - تم حذف العامل x (يساوي واحد).

باستخدام الصيغة النهائية للمشتق ، يمكننا أن نرى أننا لسنا بحاجة لحساب وظيفة الخسارة بشكل صريح (نحتاج فقط إلى مشتقات جزئية).

دعونا نتحقق من عدد الكائنات من مجموعة التدريب التي يعطيها نموذجنا الإجابات الصحيحة ، وعددها - الأشياء الخاطئة.

 i = 0 correct = 0 incorrect = 0 for item in y: if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item): correct += 1 else: incorrect += 1 i = i + 1 print(correct, incorrect) 

925 75

np.around (x) - تقريب قيمة x. بالنسبة لنا: إذا كانت x> 0.5 ، فإن القيمة هي 1. إذا كانت x ≤ 0.5 ، فإن القيمة هي 0.

وماذا سنفعل إذا كان عدد ميزات الكائن هو 5؟ 10؟ 100؟ وسيكون لدينا كمية مناسبة من الأوزان (زائد واحد للتحيز). من الواضح أن العمل يدويًا مع كل وزن ، وحساب التدرجات لأنه غير مريح.

سوف نستخدم مكتبة PyTorch الشهيرة.

PyTorch = NumPy + CUDA + Autograd (الحساب التلقائي للتدرجات)

تنفيذ PyTorch:

 import torch import numpy as np from torch.nn import Linear, Sigmoid def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step X = torch.FloatTensor(data.iloc[:,:2].values) y = torch.FloatTensor(data['target'].values.reshape((-1, 1))) from torch import optim, nn neuron = torch.nn.Sequential( Linear(2, out_features=1), Sigmoid() ) print(neuron.state_dict()) lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer) for epoch in range(n_epochs): loss = train_step(X, y) print(neuron.state_dict()) print(loss) 

OrderedDict ([('0.weight' ، موتر ([[- 0.4148 ، -0.5838]])) ، ('0.bias' ، موتر ([0.5448])]]]
OrderedDict ([('0.weight' ، موتر ([[5.4915 ، -8.2156]]]) ، ('0.bias' ، الموتر ([- 1.1130]]]]])
+0.03930133953690529

خسارة جيدة إلى حد ما على عينة الاختبار.

هنا ، تم اختيار MSELoss كدالة خسارة.

المزيد عن الخطي

باختصار: نعطي معلمتين للإدخال (لدينا x1 و x2 كما في المثال السابق) ونحصل على معلمة واحدة (ص) للإخراج ، والتي بدورها يتم تغذيتها لإدخال وظيفة التنشيط. ثم يتم حسابها بالفعل: قيمة وظيفة الخطأ ، التدرجات. في النهاية - يتم تحديث الأوزان.

المواد المستخدمة في المقال