
في أنواع التوزيع ، يتم توزيع العناصر وإعادة توزيعها في الفئات حتى يتم فرز الصفيف.
في الحالة العامة ، يحدث هذا بنفس الطريقة تقريبًا. تنتشر العناصر حسب الفئات وفقًا لبعض المعايير. إذا لم يؤدي ذلك إلى ترتيب الصفيف ، فسيتم تنقيح سمات الفئة وتناثر العناصر مرة أخرى على الفئات المكررة. ويحدث هذا حتى تصبح المجموعة مرتبة.
في عمليات الفرز حسب التوزيع ، لا توجد دائمًا مقارنات بين العناصر فيما بينها وتبادلها. الشيء الرئيسي هو ما إذا كان العنصر ينتمي إلى فئة معينة أم لا ، ومقارنتها مع العناصر الأخرى نادرا ما تلعب دورا.
عادةً ما يكون لهذه الأنواع تعقيد زمني خطي (بدلاً من لوغاريتمي ، كما هو الحال مع أنواع التبادلات أو الدمج أو الخيارات أو الإضافات الفعالة). أيضًا ، تتطلب خوارزميات هذه الفئة دائمًا الكثير من الذاكرة الإضافية ، حيث يجب تخزين العناصر التي تم تجميعها حسب الفئات في مكان ما.
أنواع التوزيع جيدة لفرز الأعداد الصحيحة والسلاسل. عادةً ما يكون فرز الأرقام الحقيقية معهم غير مريح. أيضًا ، تقوم أنواع التوزيع بفرز مصفوفات مرتبة تمامًا وتتألف من أرقام مكررة - فكلما زاد عدد مرات التكرار ، كانت الفئات الأقل حاجة مختلفة.

كُتب هذا المقال بدعم من إديسون.
رأي العملاء: 10 إيجابيات من المبرمجين من EDISON
هذا مثير للاهتمام ومفيد لمعرفة: مبرمج الإفطار
النظر في خوارزمية أن معظم محدب يوضح الخصائص المذكورة أعلاه.
فرز دلو :: فرز دلو
أسماء أخرى هي سلة الفرز ، كتلة الفرز ، والفرز جيب.
نحن نوزع الأرقام في السلال ، ثم ننتشر في كل سلة سلال أصغر ، وهكذا ، حتى في بعض المستويات في السلة ، هناك فقط نفس العناصر. ثم من هذه السلال ذات المستوى الأدنى ، من السهل استعادة الصفيف في حالة مرتبة.
دعونا شرح مع مثال محدد. دعنا نقول لدينا مجموعة غير مرتبة. من المعروف أن هذه المجموعة تحتوي على أرقام من 1 إلى 8.
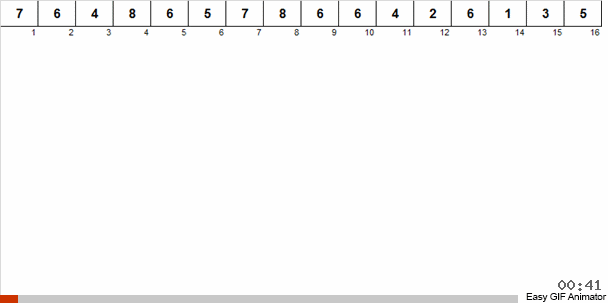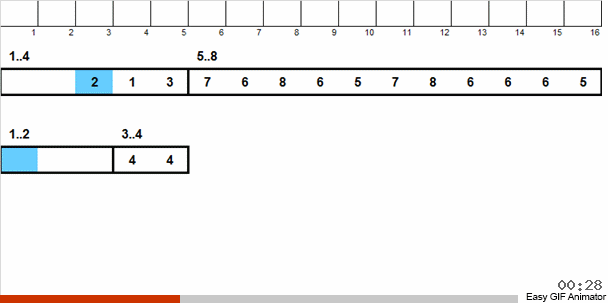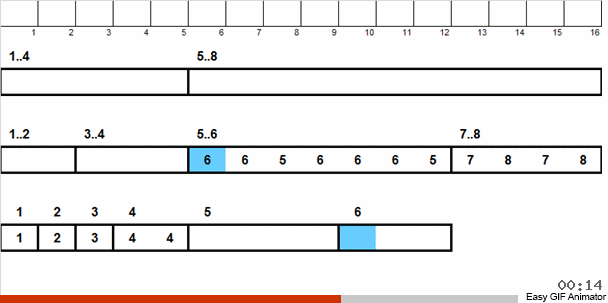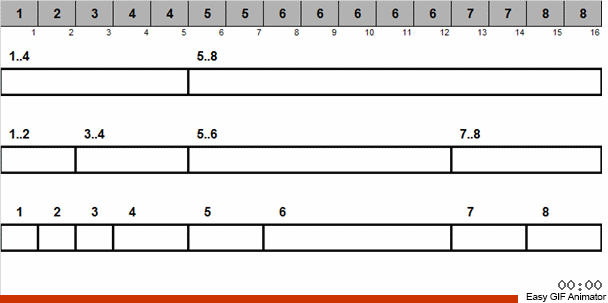
نحن نرمي هذه الأرقام إلى مجموعتين: الأرقام من 1 إلى 4 تنقسم إلى مجموعة واحدة ، من 5 إلى 8. في المجموعة الثانية ، ثم نوزع الأرقام في السلة الأولى على سلالتين: في رقم واحد 1 و 2 ، وفي المجموعة 3 و 4 الأخرى. نقوم أيضًا بتوزيع هذه السلال في سلال bast ، والتي تحتوي بالفعل على أرقام من نفس الحجم. لتلك السلة الكبيرة التي تحتوي على أرقام من 5 إلى 8 ، نطبق تكرار مماثل.
ثم ، من سلال صغيرة ، يحتوي كل منها على نفس الأرقام ، نعيد العناصر إلى الصفيف الرئيسي وفقًا للأسبقية.
لا ينطبق الفرز النووي في هذا النموذج بشكل خاص في الممارسة العملية ، ولكنه يوضح بشكل معياري كيف تعمل جميع عمليات الفرز حسب التوزيع بشكل عام.
Thanos sort :: Thanos sort
في بعض الأحيان يتم إرسال أنواع المؤلفين إلي ، وهذه مجرد حالة. وصفها المؤلف أندريه دانيلين بأنها "فرز روسي إلى نصفين" ، لكني أطلق عليها اسم فرز ثانوس. أو ، إذا تابعنا رسميًا عن الأساليب المستخدمة ، فيمكننا استدعاء الفرز المتوسط الحسابي الخاص به.
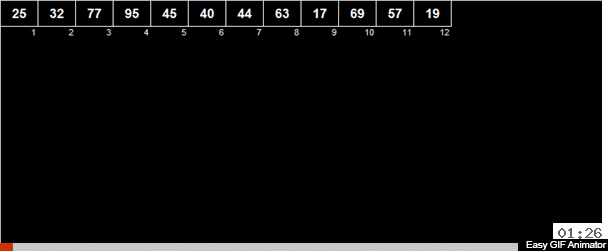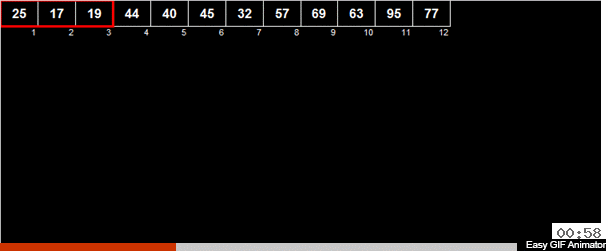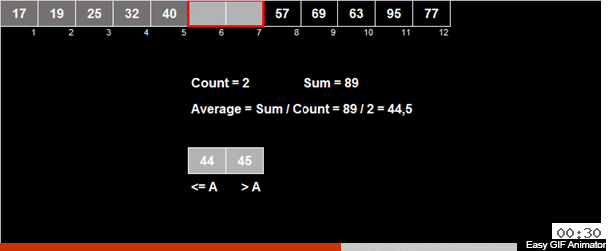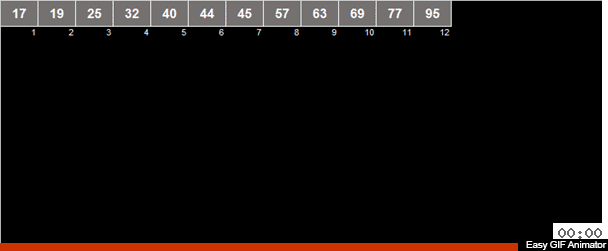
يتم حساب الوسط الحسابي للعناصر في الصفيف ثم يتم توزيع جميع العناصر في مجموعتين. في مجموعة واحدة ، توجد عناصر أصغر (أو تساوي) في الوسط الحسابي ، في المجموعة الثانية - عناصر أكبر من الوسط الحسابي. ثم يتم تطبيق نفس الإجراءات بشكل متكرر على كلتا المجموعتين - وهلم جرا إلى النهاية المريرة.
وماذا عن التيتانيوم المجنون؟ إذا كانت هذه صفيفًا عشوائيًا ، عندئذٍ ، فإن العنصر ، عند مقارنته بالمتوسط الحسابي ، لديه فرصة بنسبة 50/50 في الانتقال إلى واحدة من مجموعتين.
بالمناسبة ، على الإنترنت ، صادفت خوارزمية هزلية أخرى بنفس الاسم. إذا لم يتم فرز المصفوفة ، فانقر فوق Infinity Glove وأرسل نصف عناصر الصفيف المحددة عشوائياً إلى غير موجود. إذا كان الناجون يشكلون مجموعة مرتبة ، فيمكن اعتبار مهمتهم العظيمة قد تحققت. إن لم يكن بالفعل ، ثم يمكنك إجراء عدد قليل من النقرات.

لكن العودة إلى فرزنا التوزيع. يمكن تقسيم كل منهم إلى مجموعتين فقط -
فرز الأنواع والفرز bitwise . حسنًا ، إذا كنت تريد ذلك ، يمكنك أيضًا تمييز عمليات
فرز الأرقام ، أي تلك التي يمكن أن يعزى إلى كليهما.
هناك أيضًا خوارزميات مختلطة (هذه هي تلك التي تستخدم طرقًا لفئات مختلفة ، على سبيل المثال ، يعد فرز Tim عبارة عن مزيج من فرز الدمج وفرز الإدراج ، والفرز الاستقرائي هو فرز سريع ينتقل إلى مجموعة بيانات ، وما إلى ذلك) ، بما في ذلك فرز التوزيع ومع ذلك ، الهجينة هي قسم منفصل. عنهم في وقت لاحق.
ترتبط آلاف الفرز والحساب المتوسط الفرز لفرز العد.
فرز الأنواع
الفكرة الأساسية هي أننا نحسب عدد الأرقام في كل فصل.
فرز العد :: فرز العد
نحن نحسب عدد المرات التي يحدث فيها رقم واحد أو آخر في الصفيف. معرفة هذه الكميات ، ونحن تشكيل بسرعة مجموعة أمرت بالفعل.
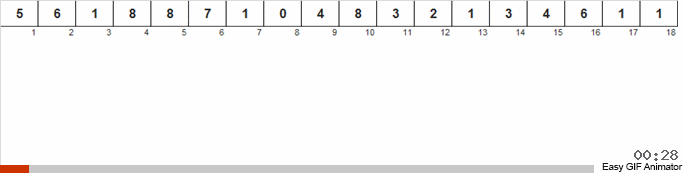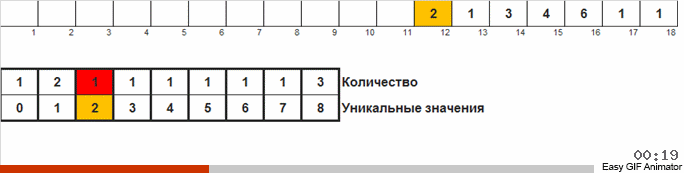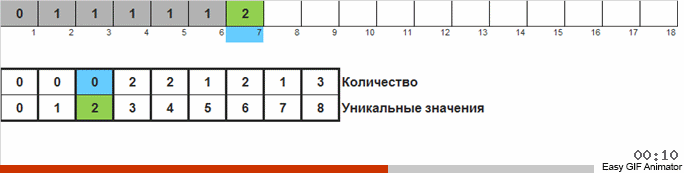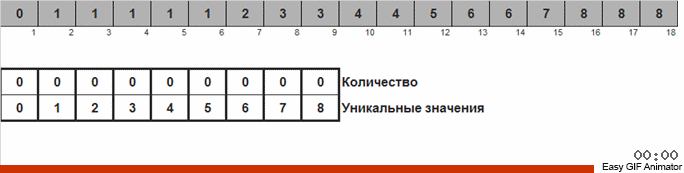
لهذا الفرز تحتاج إلى معرفة الحد الأدنى والحد الأقصى في الصفيف. ثم يتم إنشاء المفاتيح للصفيف الإضافي ، حيث نصلح ما وعدد المرات التي التقينا فيها.
رمز بايثون:
def CountingSort(array, mn, mx): count = defaultdict(int) for i in array: count[i] += 1 result = [] for j in range(mn,mx+1): result += [j]* count[j] return result
فرز حمامة :: فرز حمامة
نذهب إلى الصفيف ، إذا تم العثور على رقم جديد ، فإننا نبدأ العداد (كمفتاح لقائمة المساعدة) لهذا الرقم. إذا لم تتم مواجهة الرقم لأول مرة ، فسيتم تشغيل الزيادة لهذا العداد.
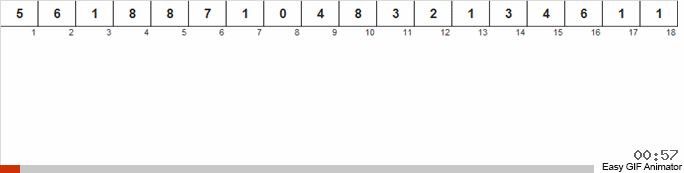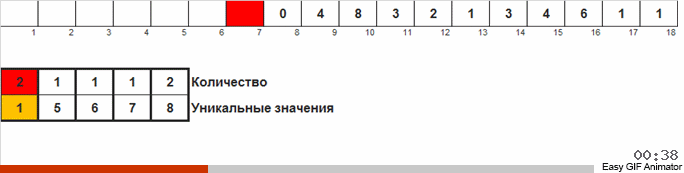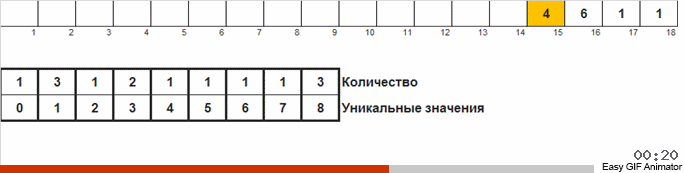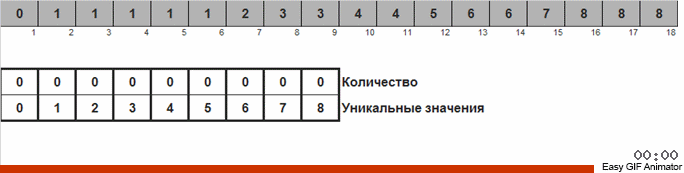
الاختلاف عن الطريقة السابقة هو أنه عند الفرز عن طريق العد ، نبدأ على الفور في عدادات لجميع الأرقام الممكنة التي قد تحدث في الصفيف (يمكننا تحمله إذا كان الحد الأقصى والحد الأدنى في الصفيف معروفان). بعض الأرقام لا تظهر أبدًا ولا تظهر عداداتها. في فرز الحمام ، نبدأ العدادات فقط لتلك الأرقام التي تحدث بالفعل في الصفيف. يتم استخدام مجموعة في فرز الفرز للعدادات ، ويتم استخدام قائمة مرتبطة مضاعفة في فرز الحمام ، والذي يسمح لك بإضافة عدادات جديدة أثناء التنقل.
تُسمى هذه الطريقة أحيانًا
بالفرز Dirichlet ، لأن الخوارزمية نفسها هي مثال على النتائج المختلفة لمبدأ Dirichlet.
إذا تم توزيع كائنات N عبر حاويات M ، و N> M ، فإن حاوية واحدة على الأقل تحتوي على أكثر من عنصر واحد.
رمز بايثون:
def PigeOnHoleSort(a): mi = min(a) size = max(a) - mi + 1 holes = [0] * size for x in a: holes[x - mi] += 1 i = 0 for count in range(size): while holes[count] > 0: holes[count] -= 1 a[i] = count + mi i += 1
الفرز قليلا
نقوم بتوزيع الأرقام وفقًا للرقم الموجود في فئة معينة من الرقم. إذا قمنا بذلك عدة مرات لأرقام مختلفة ، فسنحصل فجأة على مجموعة مرتبة.
ترتيب منخفض bitwise الفرز :: LSD نوع الجذر

ننتقل من الأرقام الأقل إلى الأرقام القديمة وفي كل تكرار نوزع عناصر المصفوفة اعتمادًا على الرقم الموجود في الرقم.
بعد التوزيع التالي ، نعيد العناصر إلى الصفيف الرئيسي بالترتيب الذي سقطت فيه العناصر في الفئات أثناء إعادة التوزيع التالية.
بالنسبة للفرز البطيء ، من المهم أن تعتبر العناصر لها نفس عدد الأرقام. إذا كان العدد الفعلي للأرقام مختلفًا ، فسيتم حل المشكلة عن طريق إضافة أصفار إضافية كأرقام أعلى.
ترتيب ارتفاع bitwise الفرز :: MSD نوع الجذر

أولاً ، نوزع بين الرتب العليا ، التي ننتقل منها إلى الرواد الأصغر سناً.
يعد تنفيذ هذا الخيار أكثر صعوبة ، حيث يتم تنفيذ الانتقال إلى الأرقام السفلية بشكل متكرر داخل الفئات ، وليس بين جميع عناصر الصفيف.
لكن هذا التعقيد يكافئه حقيقة أن MSD أسرع من LSD. عند الانتقال من الأرقام الأدنى إلى الأرقام القديمة ، يجب عليك معالجة جميع الأرقام من جميع الأرقام من أجل الفرز بشكل صحيح. إذا قمت بالانتقال من الأقدم إلى الأقدم ، فليس عليك في الواقع معالجة جميع الأرقام لجميع الأرقام ، حيث تأتي الحالة المصنفة كقاعدة عامة في وقت مبكر.
معظم الفرز bitwise هي اختلاف MSD أكثر كفاءة. هذا مفيد بشكل خاص لفرز الأوتار ؛ لذلك ، عادةً ما يتم استخدام شجرة لاحقة. سنحلل في واحدة من المقالات التالية.
عد الفرز bitwise
في بعض الأحيان ، يكون فرز التوزيع قابلاً للعد في نفس الوقت وخاصية البت.
حبة التصنيف :: حبة التصنيف

أسماء أخرى من الخوارزمية: الفرز المعداد ، والفرز الجاذبية.
لقد كتبت بالفعل عن هذا الفرز عدة مرات (
1 ،
2 ) ، لذلك سأكون مختصراً ، فقط الجوهر.
افترض أن كل رقم في صفيف هو مجموعة من الكرات ، وعدد الكرات هو قيمة الرقم. إذا رتبنا الأرقام على بعضها البعض كصفوف أفقية من هذه الكرات ثم دفعناها عموديًا ، فسنحصل على مجموعة مرتبة.
الحيلة هنا هي أننا نمثل كل رقم باستخدام الكرات في نظام رقم أحادي. وفي الحقيقة ، نحن ببساطة نحسب عدد المرات التي تحتوي فيها كل الأرقام على أرقام.
BeadSort في بيثون في سطر واحد:
بعد فترة من الوقت ، سنقوم بتحليل الفرز الأكثر تعقيدًا للعد التنازلي ، حيث يحتل فرز
العلم الأمريكي مكانًا بارزًا.
مراجع
 دلو
دلو /
دلاء ،
عد /
حمامة /
ديريتشليت ،
جذر /
تفريغ ،
حبةسلسلة المقالات:
تم تحديث تطبيق الجولاب اكسل بشكل ملحوظ. ظهرت بعض الخوارزميات من مقالة اليوم هناك لأول مرة. تحديث من يستخدم.