🐥 🚅 🐪 كل ما تريد معرفته عن البندول العكسي 🤚🏿 👩🏾‍✈️ 👩‍💻

المقالة بمثابة ورقة الغش لأولئك الذين يرغبون في جعل البندول العكسي. فيما يلي المشكلات التي أعيد صياغتها عدة مرات ، هناك حاجة إلى لمحة موجزة عن النظرية لفهم كيفية تثبيت النظام.

لماذا أحتاج هذا؟

باختصار: أردت توسيع آلة CNC الخاصة بي ، لكن حدث خطأ ما ...

القصة الكاملة

منذ الطفولة ، أردت أن يكون لدي آلة CNC الخاصة ، لأن تعاملت مع طرازات الطائرات حيث تحتاج إلى عمل الكثير من التفاصيل الصغيرة المتكررة. أولاً اشتريت مجموعة DIY جاهزة ، ثم قررت زيادتها. لقد لعبت لمدة شهرين ، ولكن لا تزال الآلة صغيرة ، كانت مساحة العمل 18 × 10 سم فقط ، ولا تحتوي على مجسات تحديد المواقع. قررت شراء دليل أكبر ، ووضع مفاتيح الحد وتثبيت العربة في الوسط باستخدام محرك السائر. لقد فعلت ذلك في نصف يوم ، لكن لا يمكنك الذهاب مباشرة إلى الحلم - فبالنسبة إلى CNC كبير ، تحتاج إلى تعقيد المهمة ووضع البندول على العربة ، ثم بدا الأمر سهلاً بالنسبة لي ، لكن كان عليّ أن أتذكر سنوات المعهد والتعرف على TAU.

محاولات فاشلة

استغرق المشروع ما يقرب من عامين من التجربة والخطأ ، وإعادة التصميم ، في انتظار التفاصيل وأيام غير مكتملة حتى يتسنى لأولئك الذين يرغبون في تكرار توفير وقتهم وأعصابهم ، وأعتقد أنه من الضروري التحدث عن القرارات غير الناجحة.

جيروسكوب (MPU6050) بدلاً من جهاز التشفير - لا شيء ضده بشكل أساسي ، ولكن يجب أن يكون المستشعر موجودًا على قضيب دوار ، وهذا يوفر تأثيرًا لا يمكن التنبؤ به وعدم القدرة على التمرير في القضيب عدة مرات حول المحور.
التشفير المطلق - إذا كان مقياس الجهد ، فحركة الأسلاك (نتيجة لوجود جهات الاتصال في arduino) تُحدث ضوضاء في القياسات ، لا يزال ADC ذي 10 بتات غير كافٍ ؛ إذا كان المستشعر أكثر تكلفة ، فإن القراءة تتم عبر واجهة تسلسلية ، وهذا يؤدي إلى تأخير في النظام ، خاصةً مع محرك السائر.
صلابة النظام - في مرحلة ما ، أخذت أنبوبًا من الألمنيوم بحمل في النهاية ، عندما اهتزت العربة ، وبدأت الاهتزازات القوية فيه ، ولم يكن من الواضح على الفور النظام الذي استقرنا عليه. يجب أن نسعى جاهدين للتأكد من أن النظام المادي هو أقرب ما يمكن على غرار ما هو نموذج.
الاحتكاك - غالباً ما يتم إهمال هذه الظاهرة ، حاولت تقليصها باستخدام عجلات عربة كبيرة ومقاطع فتحة V ، على عكس القضبان مع المتزلجون مع كرات صغيرة ، ل الاحتكاك المتداول يتناسب عكسيا مع نصف القطر.
استخدام محرك السائر - قضيت الكثير من الوقت في محاولة السير في هذا الطريق ، فمن المضلل تبسيط الصيغ (في الواقع ، نحن نتحكم فورًا في تسارع قاعدة البندول) وبساطة التصميم (يمكننا أن ننسى الاحتكاك في السكة ، ومشفير المحرك ، إذا افترضنا أن المحرك لا يتخطى الخطوات) ، ولكن ... للتحكم الدقيق في السرعة ، يجب أن يكون الوقت الفاصل بين الخطوات هو عشرات من الميكروثانية ، بحيث يمكنك نسيان إخراج الحالة إلى وحدة التحكم. بدون ملاحظات ، لا يمكنك التأكد من أن المحرك لم يفوت الخطوات وأن السرعة هي بالفعل ما يفكر فيه النظام. لا أدعي أن هذا حلاً مسدودًا ، إذا نجح شخص ما في تثبيت البندول بمحرك السائر ، سأكون سعيدًا للنظر فيه.

البندول مجانا

لإكمال الصورة ، نحاكي البندول على عربة مجانية دون احتكاك.

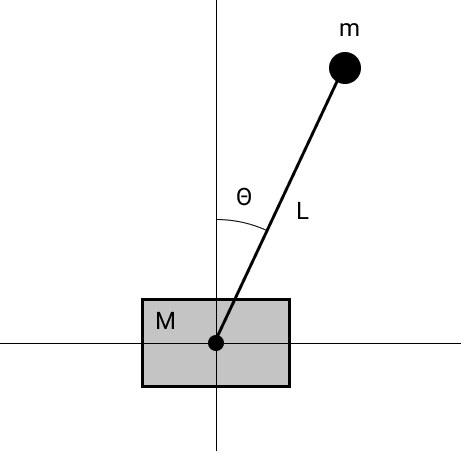
يمكن الحصول على معادلات الحركة من خلال التمييز بين Lagrangian فيما يتعلق بالإحداثيات المعممة. نحصل على المعادلات التالية:

$\ start {cases} L \ cdot \ ddot \ theta + g \ cdot {sin (\ theta)} - \ ddot {x} \ cdot {cos (th)} = 0 \\ (m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta )} = 0 \ end {cases}$

يمكنك من خلالها معرفة كيفية تغير متجه الحالة:

،

$\ start {cases} \ dot \ theta = w \\ \ dot {w} = \ frac {g \ cdot {sin (\ theta)} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin (\ theta)} \ cdot {cos (\ theta)}} {L \ cdot (1 + b \ cdot {cos ^ 2 (\ theta))}} \\ \ dot {x} = v \\ \ dot {v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {sin (\ theta)} - g \ cdot {sin (\ theta)} \ cdot {cos (\ theta)}} {1 + b \ cdot {cos ^ 2 (\ theta)}} \ end {cases}، b = \ frac {m} {M + m}$

ومحاكاة النظام. الكود هنا .

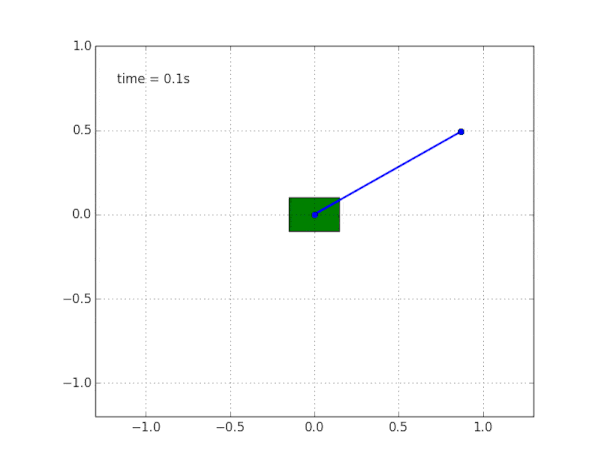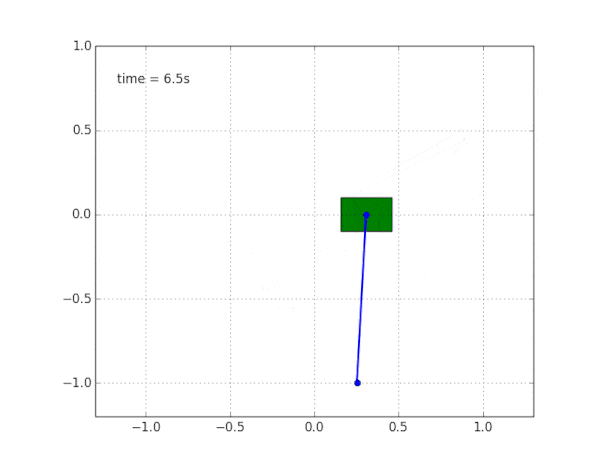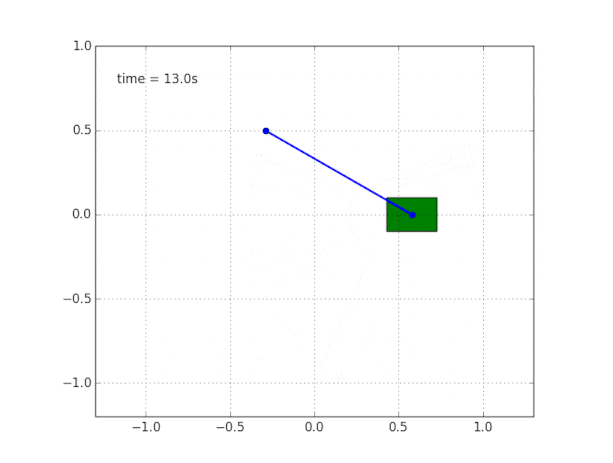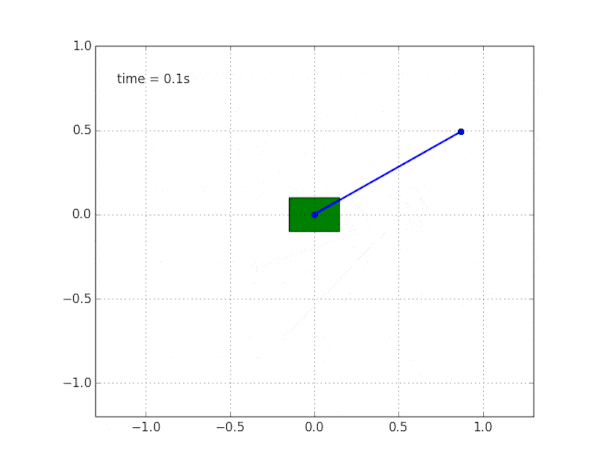
لماذا النظام غير مستقر؟

يخبرنا المنطق السليم والتصور أن البندول نفسه لن يقف. ولكن كيفية التحقق من ذلك رياضيا؟
بشكل عام ، فإن النظام الخطي والحل هما كما يلي:

،

$\ dot {\ mathbf {x}} = A \ mathbf {x} ، \ mathbf {x} (t) = e ^ {At} \ mathbf {x} (0)$

يبدو الأس في قوة المصفوفة أكثر وضوحًا إذا ذهبت إلى نظام الإحداثيات من المتجهات الإلكترونية ، ثم المصفوفة

د و ل ا

$دولا$ سيكون قطري (

$D$ ) ، وسيظهر العارض مثل:

e ^ {Dt} = \ start {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}

$e ^ {Dt} = \ start {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}$

الآن ينظر إليه ، في وجود القيم الذاتية (

$\ lambda_i$ ) مع وجود جزء حقيقي إيجابي ، فإن العنصر المقابل من متجه الحالة سيميل إلى ما لا نهاية ، وسوف ينهار النظام. ينطبق ما سبق على الأنظمة المستمرة ، ويرد وصف أكثر حول الاستدامة في هذه المحاضرة المرئية.
تحقق مما إذا كان هذا هو الحال بالنسبة للبندول العكسي. نحن خطي نظامنا بالقرب من موقف التوازن ل

، ، ،

$\ theta = 0 ، sin (\ theta) \ approx \ theta ، cos (\ theta) \ approx 1، w ^ 2 \ approx 0$ :

\ تبدأ {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ تبدأ {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ start {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}

$\ تبدأ {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ تبدأ {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ start {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}$

القيم الذاتية غير الصفرية لها النموذج

$\ pm \ sqrt {\ frac {g} {L (1 + b)}}$ ، وبالتالي أصبحنا مقتنعين بعدم الاستقرار.

أضف ملاحظات

الآن القوة ستعمل على النقل

و

$و$ ، يمكن إعادة كتابة إحدى المعادلات بالشكل:

$(m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta)} = f$ وسيأخذ النظام الخطي الشكل:

\ تبدأ {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ تبدأ {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ start {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix} + \ start {bmatrix} 0 \\ \ frac {1} {L} \ frac {1} {2m + M} \\ 0 \\ \ frac {1} {2m + M} \ end {bmatrix} \ cdot {f}

الآن النظام (

$\ dot {\ mathbf {x}} = A \ mathbf {x} + Bu$ ) أصبحت قابلة للتحكم ، ويمكن التحقق من ذلك عن طريق التحقق من أن رتبة المصفوفة

\ تبدأ {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}

$\ تبدأ {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}$ مساوية لبعد ناقل الحالة ، أي 4. للحفاظ على البندول في وضع مستقيم ، استخدمت وحدة تحكم الحالة الخطية من الدرجة الثانية ، أي التحكم (u أو f) هو نتاج متجه الحالة

، ، ،

$[\ theta، \ dot {\ theta}، x، \ dot {x}]$ بواسطة متجه من المعلمات التي تم العثور عليها مرة واحدة عن طريق التقليل من الوظيفية التربيعية . رمز المحاكاة هنا .

التحكم في المحرك

أنت الآن بحاجة إلى التحكم في محرك التيار المستمر ، فهو يحتوي على العديد من المعلمات التي لا أعرفها ، لذلك أخذتها من أجل "الصندوق الأسود" ، الموصوف بالمعادلات التالية ، مع مراعاة الاحتكاك:

$\ start {cases} \ dot {x} = v \\ \ dot {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {sign (v)} \ end {cases}$

يمكنك أن تقرأ عن اشتقاق المعادلات وتقدير المعلمة هنا . أدناه أعطي رسومات بيانية عن تسارع المحرك مع النقل اعتمادًا على الجهد (في الواقع ، يتم إخراج إشارة PWM من وحدة التحكم) والمنحنيات المجهزة.

كما أنني وجدت معاملات النموذج بواسطة القوة الغاشمة ، الكود .
وبالتالي ، فإن وحدة التحكم تعطينا التسارع المطلوب ، ومن المعادلة الثانية ، ومعرفة جميع الثوابت ، نجد الجهد.

وضع الجهاز الحقيقي معًا

الآن لدينا كل المعرفة لجمع وتحقيق الاستقرار في البندول. لقد استخدمت الحديد التالي:

اردوينو ميجا 2560 ليس UNO ، لأن اثنين من التشفير يحتاج 4 دبابيس للمقاطعات
يمنحنا التشفير الخاص بالبندول - نبضات OMRON E6B2-CWZ6C 2500 لكل ثورة - الزاوية ، نحسب السرعة الزاوية ، الدقة عالية جدًا ، لذلك كانت هناك اختلافات محدودة كافية دون تجانس ومتوسط
يوفر التشفير للمحرك - LPD3806-600BM-G5-24C 600 نبضة لكل ثورة - موضع النقل ، وحساب السرعة
محرك 12V العاصمة مع علبة تروس 5: 1
10Amp 5V-30V Motor Driver

وهكذا ، نقيس بشكل صريح زاوية البندول ، وموضع العربة ، ونحسب السرعة الزاوية للبندول وسرعة العربة - لقد حصلنا على الحالة الكاملة ، لقد وجدت معلمات وحدة التحكم باستخدام هذا البرنامج النصي. والمثير للدهشة أن كل شيء سار بسرعة كما كان. أنا مرتاح للنتيجة ، فهي تقف بل إنها تحمل كأسًا!

رمز اردوينو هنا
ما يمكن تحسينه مقارنة بالعديد من الخيارات التي يمكن العثور عليها على youtube - هذا البندول هادئ لأن PWM يتم ضبطه خارج النطاق السمعي ويتم استخدام عجلات بلاستيكية.
تبدو هذه المهمة الآن وكأنها عمل مخبري: لقياس معلمات المحرك والعثور على معاملات المنظم ، وفهم ما يحدث في وقت واحد.

ما التالي؟

أخطط لإنتاج بندول: قم بالتأرجح ، تخلص من لفائف الأسلاك ، وصنع درعًا بموصلات ملائمة حتى لا يكون من العار التبرع لبعض المدارس أو المتاحف. إذا أراد شخص ما الانضمام ، سأكون سعيدًا بوجود العديد من الأفكار الطموحة.

مراجع

وصف مفصل لمشكلة البندول معكوس
لقد مضغنا منظمًا خطيًا من الدرجة الثانية للتحكم في البندول المقلوب - هذه المقالة وفرت لي الكثير من الوقت عند بناء البندول الخاص بي
عظيم محاضرات الفيديو TAU

شكرا لاهتمامكم!

كل ما تريد معرفته عن البندول العكسي