قانون تسريع العوائد (الجزء 1)

مرحبا يا هبر! أقدم إليكم ترجمة قانون تسريع العائدات بقلم ريمون كورزويل .

7 مارس 2001

يوضح تحليل تاريخ التكنولوجيا أن عدد التغييرات التكنولوجية ينمو بشكل كبير ، على الرغم من حدسيها ، من وجهة نظر "الفطرة السليمة" ، يبدو أن التطور خطي. وهذا يعني أن التنمية التي تتجاوز مائة عام تقويمي للقرن الحادي والعشرين ستتوافق مع ما يقرب من 20000 عام من التطوير بوتيرة حالية. كما تنمو الكفاءة أو نتائج التقدم ، مثل سرعة الرقاقة أو نسبة أداء السعر ، بشكل كبير. في بعض الأحيان ، حتى معدل النمو الأسي نفسه ينمو بشكل كبير. على مدى عدة عقود ، ستتجاوز الذكاء الآلي الذكاء البشري ، مما يؤدي إلى التفرد - وهي تغييرات تكنولوجية سريعة للغاية وعميقة بحيث تمزق نسيج التاريخ البشري ذاته. ومن بين العواقب ، اندماج الذكاء البيولوجي وغير البيولوجي ، والأشخاص الخالدين الموجودين في شكل برمجيات ، والذكاء عالي المستوى للغاية الذي ينتقل عبر الكون بسرعة الضوء.

سوف تتلقى 40 تريليون دولار ببساطة عن طريق قراءة هذا المقال وفهم كل شيء. انظر أدناه للحصول على التفاصيل الكاملة. (نعم ، غالبًا ما يذهب المؤلفون إلى أي حيل لجذب انتباهكم ، لكنني جاد تمامًا في هذا البيان. لكن قبل أن أعود إلى السرد الإضافي ، اقرأ الجملة الأولى من هذه الفقرة بعناية).

الآن دعنا نعود إلى المستقبل: معظمنا يخطئ في إدراك ذلك. اعتقد أسلافنا أن المستقبل سيكون مشابهًا جدًا لحاضرهم ، والذي بدوره كان مشابهًا لماضيهم. على الرغم من وجود اتجاهات الأسية منذ آلاف السنين ، إلا أنها كانت في تلك المرحلة المبكرة جدًا عندما يكون الاتجاه الأسي ثابتًا إلى درجة أنه يبدو وكأنه أي نقص في الاتجاهات. وهكذا ، فإن افتراضاتهم ، في معظمها ، لها ما يبررها. واليوم ، بتوجيه من الحكمة الدنيوية ، يتوقع الجميع التقدم التكنولوجي التدريجي والعواقب الاجتماعية المقابلة. لكن المستقبل سيكون أكثر إثارة للدهشة مما يدركه معظم المراقبين: القليل منهم فقط أدركوا حقيقة أن سرعة التغيير ذاتها تتسارع.

عرض خطي حدسي مقابل عرض الأسي التاريخي

إن معظم التنبؤات طويلة المدى حول الجدوى التقنية في الفترات المستقبلية من الزمن تقلل بشكل كبير من قوة التقنيات المستقبلية ، لأنها تستند إلى ما أسميه نظرة "خطية حدسيّة" للتقدم التكنولوجي ، بدلاً من وجهة نظر "تاريخية أسيّة". بمعنى آخر ، ليس هذا هو الحال عندما يتوقع المرء مائة عام من التقدم من القرن الحادي والعشرين ، بدلاً من ذلك ، سوف نشهد عشرون ألف سنة من التقدم (إذا كنا نقصد التقدم بخطى الحالية ).

غالبًا ما يحدث هذا التناقض في وجهات النظر في مواقف مختلفة ، على سبيل المثال ، عند مناقشة القضايا الأخلاقية التي أثارها بيل جوي في مقالته WIRED المثيرة للجدل ، "لماذا لا نحتاج إلى المستقبل" . غالبًا ما يتقاطع بيل وأنا في اجتماعات مختلفة ، ولعبنا دور متفائل ومتشائم ، على التوالي. وبينما من المتوقع أن ينتقد مناصري موقف بيل مني ، وأرى حقًا وجود عيوب في مفهوم "الرفض" الذي اقترحه ، مع ذلك ، كقاعدة عامة ، في النهاية ، أدافع عن جوي في قضية الجدوى الرئيسية. في الآونة الأخيرة ، رفض أحد المتحدثين ، الحائز على جائزة نوبل ، مخاوف بيل ، قائلاً: "لا نتوقع أن نرى كائنات هندسية متناهية الصغر تتكاثر ذاتياً بمئات السنين الأخرى". لقد لاحظت أن 100 عام هو في الواقع تقدير معقول للوقت اللازم للتقدم التكنولوجي لتحقيق هذا الهدف المحدد ، مع سرعة تطوره اليوم. ولكن بما أن وتيرة التقدم تتضاعف كل عشر سنوات ، فسنشهد قرنًا من التقدم بسرعة اليوم في 25 عامًا تقويميًا فقط.

عندما يفكر الناس في المضارع في المستقبل ، فإنهم يفترضون بشكل حدسي أن السرعة الحالية للتقدم ستستمر في المستقبل. ومع ذلك ، فإن الفحص الدقيق لسرعة تطوير التكنولوجيا يدل على أن سرعة التقدم ليست ثابتة ، وأنه من الطبيعة البشرية أن تتكيف مع الوتيرة المتغيرة بحيث يبدو الحدس ثابتًا بشكل حدسي. حتى بالنسبة لأولئك منا الذين عاشوا فترة طويلة بما يكفي ليشعروا كيف تتسارع الخطى مع مرور الوقت ، فإن الحدس الطبيعي لدينا يعطي الانطباع بأن التقدم يسير بنفس السرعة التي شعرنا بها مؤخرًا. من وجهة نظر عالم الرياضيات ، السبب الرئيسي لذلك هو أن الأس في المقاطع القصيرة يتم تقريبه بخط مستقيم. لذلك ، على الرغم من أن وتيرة التقدم في الماضي القريب (على سبيل المثال ، في العام الماضي) كانت أعلى بكثير مما كانت عليه قبل عشر سنوات (ناهيك عن مائة أو ألف سنة مضت) ، فإن تجربتنا الأخيرة تسيطر على الذكريات. لذلك ، من الشائع تمامًا أن يقوم المعلقون المتطورون ، الذين يناقشون المستقبل ، كأساس لتوقعاتهم ، باستكمال معدل التغير الحالي خلال السنوات العشر أو المائة القادمة. هذا هو السبب في أنني أسمي هذا النوع من النظرة المستقبلية على وجهة نظر "الخطية حدسي".

يظهر التقييم الجدي لتاريخ التكنولوجيا أن التغير التكنولوجي أسي. مع النمو الهائل ، نجد أن المؤشر الرئيسي ، مثل القدرة الحاسوبية ، مضروب في معامل ثابت لكل وحدة زمنية (على سبيل المثال ، يتضاعف كل عام) ، وليس فقط يزيد بمقدار معين. النمو الأسي هو سمة مميزة لأي عملية تطورية ، ويمكن أن يكون التطور التكنولوجي مثالاً جيدًا.

من الممكن تقييم البيانات بطرق مختلفة ، وفي نطاقات زمنية مختلفة ، ولمجموعة واسعة من التقنيات ، من إلكتروني إلى بيولوجي ، مع ملاحظة تسارع التقدم ومعدل نموها. في الواقع ، فإننا لا نجد النمو الأسي فحسب ، بل النمو الأسي "المزدوج" ، أي أن معدل النمو الأسي نفسه ينمو بشكل كبير. لا تنطبق هذه الملاحظات فقط على افتراض استمرار قانون مور (أي انخفاض كبير في حجم الترانزستورات في دائرة متكاملة) ، ولكنها تستند إلى نموذج تمثيلي لمختلف العمليات التكنولوجية. هذا يدل بوضوح على أن التكنولوجيا ، وخاصة سرعة التغير التكنولوجي ، تتسارع في (على الأقل) تقدم هندسي ، وليس خطيًا ، وهذا يحدث من لحظة ظهور التكنولوجيا والتكنولوجيا ، ولكن في الحقيقة ، من لحظة التطور على الارض

أشدد على هذه النقطة ، لأن المتنبئين الذين يفكرون في الاتجاهات المستقبلية ويتحدثون عن مستقبل محتمل يرتكبون خطأ فادحًا. تتجاهل معظم التوقعات التكنولوجية عمومًا النوع "التاريخي الأسي" من التقدم التكنولوجي. هذا هو السبب في أن الناس يميلون إلى المبالغة في تقدير ما يمكن تحقيقه على المدى القصير (لأننا نميل إلى تجاهل التفاصيل الضرورية) ، ولكن نقلل مما يمكن تحقيقه على المدى الطويل (لأنه يتم تجاهل النمو المتسارع).

قانون العائدات المتسارعة

يمكننا تنظيم هذه الملاحظات في ما أسميه قانون تسريع العوائد ، على النحو التالي:

• يستخدم Evolution ردود فعل إيجابية بطريقة تستخدم أساليب أكثر فاعلية ناتجة عن مرحلة واحدة من التقدم التطوري لإنشاء المرحلة التالية. نتيجة لذلك
• معدل تطور عملية تطورية يزيد أضعافا مضاعفة مع مرور الوقت. بمرور الوقت ، يزداد "ترتيب" المعلومات المتضمنة في العملية التطورية (أي ، قياس مدى ملائمة هذه المعلومات للهدف ، أي البقاء في عملية التطور).
• تبعا لذلك ، فإن "عودة" العملية التطورية (على سبيل المثال ، السرعة ، الفعالية من حيث التكلفة ، أو "القوة" الكلية للعملية) تنمو باطراد بمرور الوقت.
• في سلسلة أخرى من ردود الفعل الإيجابية ، كعملية تطورية معينة (على سبيل المثال ، حساب) تصبح أكثر كفاءة (على سبيل المثال ، فعالة من حيث التكلفة) ، يتم تخصيص المزيد والمزيد من الموارد لمواصلة تطوير هذه العملية. وهذا يؤدي إلى المستوى الثاني من النمو الأسي (أي معدل النمو الأسي نفسه ينمو بشكل كبير).
• التطور البيولوجي هو واحد من هذه العملية التطورية.
• التطور التكنولوجي هو عملية تطورية أخرى. في الواقع ، أدى ظهور النوع الأول الذي يخلق التكنولوجيا إلى عملية تطورية جديدة للتكنولوجيا. وبالتالي ، التطور التكنولوجي هو نتاج واستمرار التطور البيولوجي.
• يوفر نموذج معين (طريقة أو نهج لحل مشكلة ، على سبيل المثال ، تقليل منطقة الترانزستور في دائرة متكاملة ، كنهج لإنشاء أجهزة كمبيوتر أكثر قوة) نموًا كبيرًا إلى أن تصل الطريقة إلى كامل إمكاناتها. عندما يحدث هذا ، يحدث تحول نموذجي (أي تغيير أساسي في النهج) يتيح استمرار النمو المتسارع.

إذا طبقنا هذه المبادئ على أعلى مستوى من التطور على الأرض ، فإن الخطوة الأولى ، وهي إنشاء الخلايا ، قدمت نموذج البيولوجيا. قدم ظهور الحمض النووي اللاحق طريقة رقمية لتسجيل نتائج التجارب التطورية. بعد ذلك ، تسبب تطور النوع الذي يجمع بين التفكير العقلاني والإصبع المقابل (أي الإبهام) في تحول نموذجي أساسي من البيولوجيا إلى التكنولوجيا. التغيير القادم في النموذج الرئيسي سيكون من التفكير البيولوجي إلى الهجين ، والجمع بين التفكير البيولوجي وغير البيولوجي. سوف يشمل هذا الهجين عمليات التمثيل الغذائي الناتجة عن إعادة بناء ونسخ مبادئ الدماغ البيولوجي.

دراسة توقيت هذه المراحل ، نرى أن العملية تتسارع باستمرار. استغرق تطور أشكال الحياة مليارات السنين للخطوات الأولى (على سبيل المثال ، للخلايا البسيطة) ؛ مزيد من التقدم تسارع. خلال الانفجار الكمبري ، استغرقت التغييرات في النماذج الأساسية عشرات الملايين من السنين فقط. في وقت لاحق ، تطورت Humanoids على مدى عدة ملايين من السنين ، وهومو العاقل فقط بضع مئات من الآلاف.

مع ظهور الأنواع المنتجة للتكنولوجيا ، أصبحت الوتيرة الأسية سريعة للغاية بالنسبة للتطور من خلال تخليق البروتين الذي يحركه الدنا وتحولت إلى تكنولوجيات من صنع الإنسان. التكنولوجيا تتجاوز صنع أداة بسيطة. إنها عملية لإنشاء تقنيات أكثر قوة باستخدام أدوات من الجولة السابقة من الابتكار. وبهذا المعنى ، تختلف التكنولوجيا البشرية عن إنتاج الأدوات في الأنواع الأخرى. كل مرحلة من مراحل تطوير التكنولوجيا ثابتة ، وتعمل كأساس للمرحلة التالية.

الخطوات التكنولوجية الأولى (الأدوات الحجرية ، النار ، العجلة) استغرقت عشرات الآلاف من السنين. بالنسبة للأشخاص الذين يعيشون في تلك الحقبة ، كانت التغييرات التكنولوجية ، حتى على مدى آلاف السنين ، بالكاد ملحوظة. بحلول عام 1000 ميلادي ، كان التقدم أسرع بكثير ، وحدث تحول في قرن واحد أو قرنين فقط. في القرن التاسع عشر ، شهدنا تغيرًا تكنولوجيًا أكثر مما كان عليه الحال في القرون التسعة التي سبقته. بعد ذلك ، في السنوات العشرين الأولى من القرن العشرين ، شهدنا تطوراً أكثر أهمية من القرن التاسع عشر بأكمله. الآن تحول النموذج يحدث في بضع سنوات فقط. شبكة الويب العالمية ، في شكلها الحالي ، لم تكن موجودة قبل بضع سنوات فقط ، وقبل عشر سنوات لم تكن موجودة على الإطلاق.

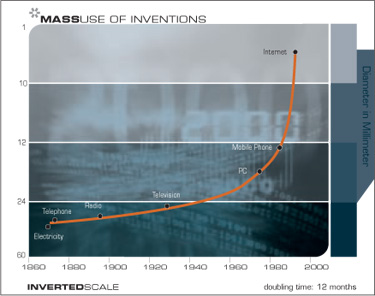
معدل التحول في النموذج (أي المعدل الإجمالي للتقدم التكنولوجي) يتضاعف حالياً (تقريبًا) كل عقد ؛ وهذا يعني أن وقت حدوث تحول في النموذج يتم تخفيضه إلى النصف كل عشر سنوات (ومعدل النمو نفسه ينمو بشكل كبير). وبالتالي ، فإن التقدم التكنولوجي في القرن الحادي والعشرين سيكون معادلاً لما كان سيتطلب (في تمثيل خطي) حوالي 200 قرن. على العكس من ذلك ، لم يمر القرن العشرين سوى 25 عامًا من التقدم (مرة أخرى ، من حيث وتيرته الحالية) ، بسبب زيادة في سرعته إلى القرن الحالي. وهكذا ، سيشهد القرن الحادي والعشرين تغيرات تكنولوجية أكبر بنحو ألف مرة من سابقتها.

التفرد وثيق

من أجل تقدير طبيعة وأهمية "التفرد" المقبل ، من المهم فهم طبيعة النمو المتسارع. تحقيقًا لهذه الغاية ، أود أن أحكي قصة عن مخترع لعبة الشطرنج وراعيها ، إمبراطور الصين. استجابةً لعرض الإمبراطور بتعيين مكافأة لعبته المفضلة الجديدة ، طلب المخترع وضع حبة من الأرز في المربع الأول من رقعة الشطرنج ، اثنتان في المربع الثاني ، وأربعة في المربع الثالث ، وهكذا. وافق الإمبراطور بسرعة على هذا الطلب البسيط والمتواضع. وفقًا لإصدار واحد من هذه القصة ، أفلست الإمبراطور ، حيث شكل 63 من الزوجي ، في نهاية المطاف ، 18 مليون تريليون حبة من الأرز. بالنظر إلى أن عشرة حبات من الأرز تغطي بوصة مربعة ، فإن هذه الكمية من الأرز تتطلب حقول أرز تغطي ضعف كامل سطح الأرض ، بما في ذلك المحيطات. في نسخة أخرى من هذه القصة ، فقد المخترع رأسه.

تجدر الإشارة إلى أنه عندما ملأ الإمبراطور والمخترع النصف الأول من رقعة الشطرنج ، سار كل شيء على ما يرام. تم سكب المخترع ملاعق من الأرز ، ثم وعاء من الأرز ، ثم برميل. بحلول نهاية النصف الأول من رقعة الشطرنج ، كان لدى المخترع بالفعل حقل أرز كبير (4 مليارات حبة) ، ولاحظ الإمبراطور أن هناك شيئًا ما غير صحيح. عندما انتقلوا إلى النصف الثاني من رقعة الشطرنج ، بدأ الوضع في التدهور بسرعة. بالمناسبة ، فيما يتعلق بمضاعفة الحسابات ، منذ اختراع أول أجهزة كمبيوتر قابلة للبرمجة في نهاية الحرب العالمية الثانية ، في الوقت الحالي ، تجاوزنا قليلاً ما يزيد عن اثنين وثلاثين ضعفًا من إنتاجيتها.

هذه هي طبيعة النمو الأسي. على الرغم من أن التكنولوجيا تنمو بشكل كبير ، نحن البشر نعيش في عالم خطي. ولهذا السبب ، فإن الاتجاهات التكنولوجية لا تبدو لنا مثل الخطوات الأولية في عملية مضاعفة القوة التكنولوجية باستمرار. ثم ، على ما يبدو من العدم ، تظهر التكنولوجيا نمواً هائلاً. على سبيل المثال ، عندما انتقلت الإنترنت من 20.000 إلى 80000 نقطة خلال عامين في الثمانينيات ، ظل هذا التقدم مخفيًا عن عامة الناس. بعد عشر سنوات ، عندما نمت من 20 مليون إلى 80 مليون عقد خلال نفس الفترة الزمنية ، كان التأثير ملحوظًا بالفعل.

مع استمرار النمو المتسارع في النصف الأول من القرن الحادي والعشرين ، سيكون لدينا شعور بانفجار اللانهاية ، على الأقل من وجهة نظر أناس حديثين محدودين بمنظور خطي. التقدم ، في نهاية المطاف ، سيبدأ يحدث بسرعة بحيث سيؤدي إلى تدمير قدرتنا على مواكبة ذلك. سوف يخرج حرفيا عن سيطرتنا. سيتم تبديد الوهم بأنه يمكننا "سحب التبديل".

هل يمكن أن يستمر التقدم التكنولوجي في تسريع الإعلان اللانهائي؟ هل هناك لحظة عندما يكون الناس غير قادرين على التفكير بسرعة لمواكبة ذلك؟ أما بالنسبة للناس العاديين ، فمن الواضح أن هذا هو الحال. ومع ذلك ، ما الذي يمكن أن يحققه ألف عالم ، وكل واحد منهم أذكى ألف مرة من عالم اليوم ، وكل واحد منهم يعمل بشكل أسرع ألف مرة من الأشخاص المعاصرين (لأن معالجة المعلومات في أدمغتهم غير البيولوجية بشكل أسرع)؟ سنة واحدة يمكن أن تساوي الألفية. ما الذي سيأتي به؟

حسنًا ، أولاً وقبل كل شيء ، سيصلون إلى تقنية لتصبح أكثر ذكاءً (لأن ذكائهم لم يعد محدودًا في السلطة). سيبدأون في تغيير عمليات التفكير الخاصة بهم من أجل التفكير بشكل أسرع. عندما يتطور العلماء ليكونوا أكثر ذكاءً ويعملون مليون مرة أسرع مليون مرة ، ستكون ساعاتهم مساوية لقرن كامل من التقدم (وفقًا لمعايير اليوم).

سيكون هذا التفرد. التفرد هو التغير التكنولوجي الذي يكون سريعًا وعميقًا لدرجة أنه يكسر نسيج تاريخ البشرية ذاته. سيقول البعض أنه من المستحيل فهم التفرد ، على الأقل بمستوى فهمنا الحالي ، وبالتالي ، من المستحيل أن ننظر إلى ما وراء "أفق الحدث" وفهم ما سيحدث بعد ذلك.

رأيي هو أنه على الرغم من القيود الخطيرة على التفكير التي يفرضها دماغنا البيولوجي ، والتي لا تملك سوى مائة تريليون صلات داخلية ، إلا أننا نملك قوة تفكير تجريدي كافية لاستخلاص استنتاجات مهمة حول طبيعة الحياة بعد التفرد. الشيء الأكثر أهمية ، من وجهة نظري ، هو أن الفكر الناشئ سيستمر في تمثيل الحضارة الإنسانية ، التي هي بالفعل آلة إنسانية. وستكون هذه هي الخطوة التالية في التطور ، التحول التالي رفيع المستوى.

من أجل تقييم مفهوم التفرد في المنظور ، دعونا نلقي نظرة على تاريخ الكلمة نفسها. — , . , , , . , , . , . , , , , . , .

1950- (John Von Neumann) , « … , , , .» 1960- , (Irving John Good) « », , . 1986 , (Vernor Vinge), - (San Diego State University), «» - . , 1993 , , , , , , , « , », .

, . , , , . , , , , . , , . , «» , . , , .

, 1980- , « » , , , , . 20 , , , , .

. . , . ( ) , . , , . , , , , .

, , , . , «» , , . , : , , , -, , . , , .

, , , , .

, , . , , « ». , , Intel, 1970- , 24 . , , , , .

, 2019 . , , . , ?

.

( ) $1000 ( ) 49 , , .

, , , .

, , .

, , , -. ( ), , 1890 , «Robinson», , , CBS, , , , , , ( ) .

- . 49 ( ), . , , . , . ( ) 1910 1950 , 1950 1966 , .

? ? . « », (Randy Isaac), IBM? - ?

, ( ) , . . : , MIPS- ( ) , MIPS- .

, , . ( ), , , . «» ( , , , , ). , , , , , , , .

, ( 1958 ), ( 1947 ), , 1890 1900 . , .

من الواضح أن ما سيكون النموذج السادس بعد قانون مور قد استنفد في العقد الثاني من هذا القرن. الرقائق مسطحة اليوم (على الرغم من أن ما يصل إلى 20 طبقة من المواد لإنتاج طبقة واحدة من الدائرة). في المقابل ، يتم تنظيم دماغنا في ثلاثة أبعاد. نحن نعيش في عالم ثلاثي الأبعاد ، لماذا لا نستخدم البعد الثالث؟ يستخدم العقل البشري في الواقع عملية الحوسبة التناظرية الكهروكيميائية غير الفعالة للغاية والتي يتم التحكم فيها رقميًا. يتم إجراء معظم الحسابات في اتصالات interneuron بسرعة حوالي 200 عملية في الثانية فقط (في كل اتصال) ، وهو أبطأ بنحو عشرة ملايين مرة من الدوائر الإلكترونية الحديثة. لكن الدماغ يستمد قوته لالتقاط الأنفاس من تنظيمه المتوازي للغاية في ثلاثة أبعاد. هناك بالفعل العديد من التقنيات على الطريقة التي تعمل في ثلاثة أبعاد. على سبيل المثال ، تقوم الأنابيب النانوية التي تعمل بالفعل في المختبرات ببناء دوائر من صفائف خماسية من ذرات الكربون. ستكون الدائرة المكونة من خمسة عشر سنتيمترا مكعبة من الأنابيب النانوية أقوى بمليون مرة من المخ البشري. يتم التحقيق في أكثر من كافية من تقنيات الكمبيوتر الجديدة ، بما في ذلك رقائق السيليكون ثلاثية الأبعاد ، والحسابات البصرية ، والحسابات البلورية ، والحسابات القائمة على الحمض النووي ، والحسابات الكمية ، من أجل الحفاظ على تأثير قانون العائد المتسارع ، كما هو مطبق على تكنولوجيا الكمبيوتر ، لفترة طويلة.

وبالتالي ، فإن النمو الأسي (المزدوج) للحوسبة أوسع من قانون مور ، الذي يشير فقط إلى أحد نماذج هذا النمو. وهذا التسارع في تطوير تكنولوجيا الكمبيوتر ، بدوره ، هو جزء من ظاهرة أوسع من تسارع وتيرة أي عملية تطورية. يسارع النقاد إلى الإشارة إلى أن استقراء الاتجاه الأسي يقتصر على نفاد "الموارد". المثال الكلاسيكي هو الموقف التالي: عندما يظهر نوع ما في موطن جديد (على سبيل المثال ، الأرانب في أستراليا) ، فإن عدد الأنواع ينمو بشكل كبير لبعض الوقت ، ولكن عندما تنفد الموارد ، مثل المكان والطعام ، يحد العدد من حد النمو .

لكن الموارد الكامنة وراء النمو الأسي للعملية التطورية غير محدودة نسبياً:

1. ترتيب (تزايد مستمر) للعملية التطورية نفسها. توفر كل مرحلة من مراحل التطور أدوات أكثر قوة في المرحلة التالية. في التطور البيولوجي ، وفر ظهور الحمض النووي الأساس لـ "تجارب" تطورية أكثر قوة وأسرع. في وقت لاحق ، فتح ظهور "هياكل" مختلفة من الكائنات الحية خلال الانفجار الكمبري الطريق أمام التطور التطوري السريع لأعضاء الجسم الأخرى ، مثل الدماغ. أو لأخذ مثال أكثر حداثة ، يمكن أن يؤدي ظهور أدوات التصميم المدعومة بالكمبيوتر إلى تسريع إنشاء الجيل التالي من أجهزة الكمبيوتر.
2. "فوضى" البيئة التي تحدث فيها العملية التطورية والتي توفر خيارات لمزيد من التنوع. في التطور البيولوجي ، يدخل التنوع في شكل طفرات وظروف بيئية متغيرة باستمرار. في التطور التكنولوجي ، يأتي دعم عملية الابتكار على حساب الإبداع البشري إلى جانب ظروف السوق المتغيرة باستمرار.

المشكلة الحقيقية هي أقصى إمكانيات للمادة والطاقة ، حيث تعمل العمليات الفكرية. لكن وفقًا لنماذجي ، لن نذهب إلى حدودها خلال القرن الحالي (ولكن هذا سيصبح مشكلة في القرنين التاليين).

نحتاج أيضًا إلى التمييز بين "منحنى على شكل حرف S" ("منحنى على شكل حرف S" يمتد إلى اليمين ، والذي يتضمن نموًا بطيئًا جدًا وغير محسوس تقريبًا ، يليه نمو سريع جدًا ، ثم تسويته ، حيث تقترب العملية من خط مقارب) لأي نموذج تكنولوجي معين ، وخاصية النمو الأسية المستمرة للتطور التطوري المستمر للتكنولوجيا. نماذج محددة ، مثل قانون مور ، وصلت في النهاية إلى مستويات لم يعد النمو الهائل فيها ممكنًا. وبالتالي ، فإن قانون مور هو منحنى على شكل S. ومع ذلك ، فإن نمو قوة الحوسبة هو عملية أسية مستمرة (على الأقل حتى "تشبع" الكون بفكر حضارتنا البشرية والآلية ، لكن هذا لن يصبح قيدًا في القرن القادم). وفقًا لقانون العائدات المتسارعة ، فإن تحول النموذج ، الذي يطلق عليه أيضًا الابتكار ، يحول منحنى S لنموذج معين إلى استمرار للنمو المتسارع. يبدأ نموذج جديد (على سبيل المثال ، مخططات ثلاثية الأبعاد) في الغلبة عندما يقترب النموذج القديم من الحد الطبيعي. في تاريخ الحوسبة ، حدث هذا بالفعل أربع مرات على الأقل. تميز هذه الميزة أيضًا تصنيع الأدوات لأنواع أخرى من الحيوانات التي تتميز فيها مهارة تصنيع (أو استخدام) الأدوات لكل حيوان على حدة بمنحنى تعليمي حاد الشكل على شكل حرف S ، عن التقنيات التي أنشأها البشر والتي لها معدل نمو هائل منذ الخلق.

تسلسل الحمض النووي ، والذاكرة ، والاتصالات ، والإنترنت والتصغير

ينطبق "قانون تسريع العائدات" على أي تقنية ، وعلى أي عملية تطورية حقيقية ، ويمكن قياسها بدقة مذهلة لتكنولوجيا المعلومات. هناك العديد من الأمثلة على النمو الهائل الناشئ عن قانون تسريع العائدات ، في مجالات تكنولوجية متنوعة مثل تسلسل الحمض النووي وسرعة الاتصال والإلكترونيات بجميع أنواعها وحتى في الأحجام التكنولوجية المميزة المتسارعة. لا ينشأ التفرد من انفجار أسي واحد للسرعة الحسابية ، بل ينشأ عن التفاعل والتآزر الناتج عن التداخل المتنوع لمختلف الثورات التكنولوجية. يجب عليك أيضًا أن تضع في اعتبارك أن كل نقطة على منحنيات النمو الأسي التي تقوم عليها هذه الترسانة من التقنيات (انظر الرسوم البيانية أدناه) تمثل دراما إنسانية خطيرة من الابتكار والمنافسة. والمثير للدهشة أن هذه العمليات الفوضوية تؤدي إلى مثل هذا الاعتماد الأسي السلس والمتوقع.

على سبيل المثال ، عندما بدأ تسلسل الجينوم البشري قبل أربعة عشر عامًا ، اعتقد النقاد أنه نظرًا لسرعة التسلسل التي كانت متاحة آنذاك ، فقد يستغرق إكمال المشروع عدة آلاف من السنين. ومع ذلك ، للعام الخامس عشر ، تم الانتهاء من المشروع ، قبل الموعد المحدد بقليل.

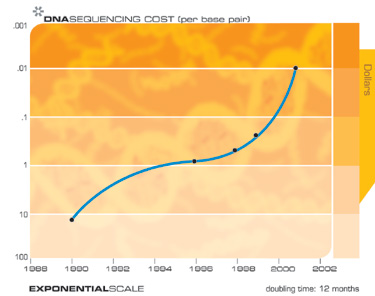
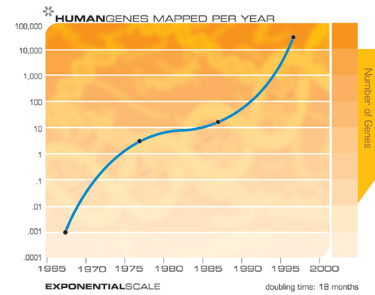
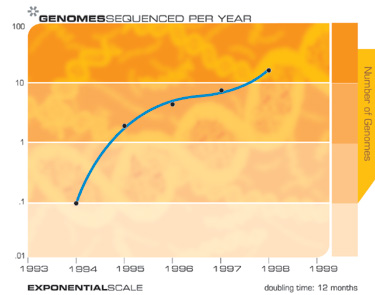
بالطبع ، نتوقع أن نرى نمواً هائلاً في تكنولوجيا أجهزة التخزين الإلكترونية مثل ذاكرة الوصول العشوائي (ذاكرة الوصول العشوائي).

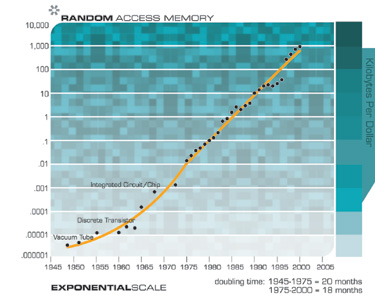
لاحظ كيف استمر النمو الهائل مع تحول النموذج من أنابيب الفراغ إلى الترانزستورات المنفصلة وما وراءها ، إلى الدوائر المتكاملة.

لا يرتبط تطوير تقنية الذاكرة المغناطيسية ارتباطًا مباشرًا بقانون مور ، ولكنه يعتمد على التقدم في مجال الأنظمة الميكانيكية والكهرومغناطيسية.

كان النمو الهائل في مجال تقنيات الاتصالات أكثر انفجارًا من مجال الحوسبة ، ولم يكن أقل أهمية في نتائجه. مرة أخرى ، هذا التسارع له قاعدة أوسع بكثير من مجرد تقليل حجم الترانزستورات على رقاقة ، ويشمل التقدم المتسارع في مجال الألياف البصرية ، والتبديل البصري ، والتكنولوجيا الكهرومغناطيسية ، وأكثر من ذلك بكثير.

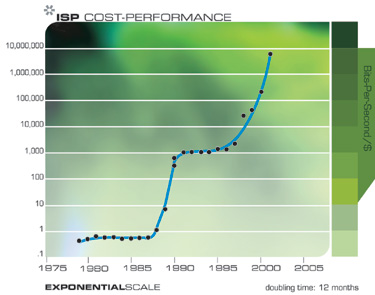
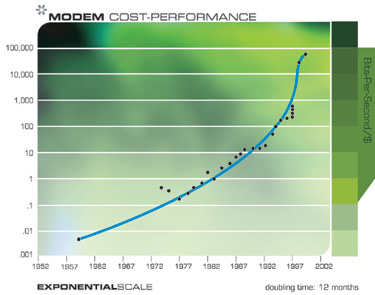
انتبه إلى سلسلة من المنحنيات الصغيرة "على شكل حرف S"

لاحظ أنه في هذين الرسمين البيانيين ، يمكننا في الواقع رؤية تقدم المنحنيات "على شكل حرف S": التسارع بسبب النموذج الجديد ، ثم الاستقرار عند اختفاء النموذج ، والاستئناف اللاحق للنمو السريع بعد تحول النموذج.

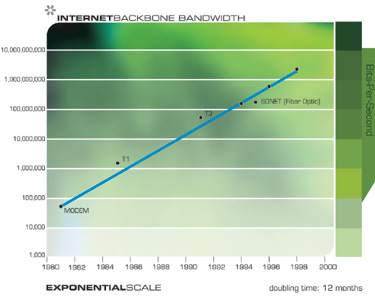
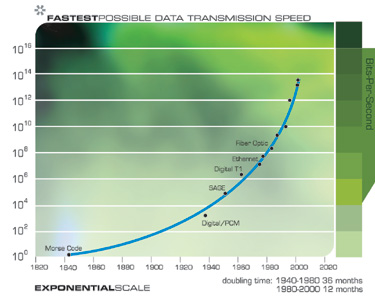
يوضح المخططان التاليان النمو الإجمالي للإنترنت ، معبراً عنه في عدد من المواقع. هذه الرسوم البيانية مبنية على نفس البيانات ، لكن أحدهما على مقياس الأسي ، والآخر خطي. كما أشرت سابقًا ، يبدو أن التقدم التكنولوجي بخطى متسارعة يتطور خطيًا. وبالتالي ، يبدو لمعظم المراقبين أنه حتى منتصف التسعينيات ، عندما ، على ما يبدو ، من أي مكان ، ظهرت شبكة الويب العالمية والبريد الإلكتروني على الفور ، لم يحدث شيء. لكن تحول الإنترنت إلى ظاهرة عالمية كان يمكن التنبؤ به بسهولة قبل ذلك بكثير ، استنادًا إلى بيانات من الاتجاه الأسي.

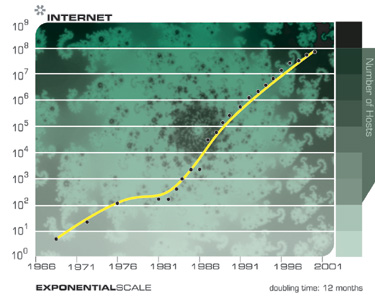
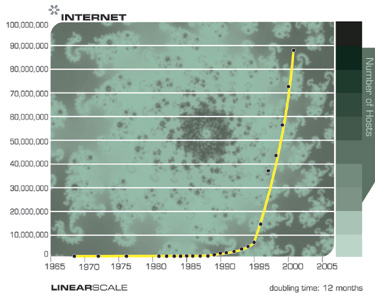
انتبه إلى ما يشبه المفاجأة في النمو الهائل للإنترنت على مخطط خطي ، وكيف يمكن التنبؤ به على الرسم البياني الأسي.

في النهاية ، سوف نهرب من فوضى الأسلاك في مدننا وفي حياتنا إلى الاتصالات اللاسلكية ، التي تتضاعف إنتاجيتها كل 10 إلى 11 شهرًا.

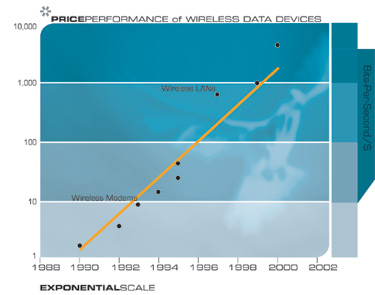
ومن التقنيات الأخرى التي ستكون لها عواقب بعيدة المدى للقرن الحادي والعشرين الميل الواسع إلى جعل الأشياء أصغر ، أي التصغير. يتم تقليل الأبعاد المميزة لعناصر مجموعة واسعة من التقنيات ، الإلكترونية والميكانيكية ، وكذلك بمعدل مضاعف. حاليا ، يحدث انخفاض في الأبعاد الخطية لكل بعد بمعامل حوالي 5.6 لكل عقد.

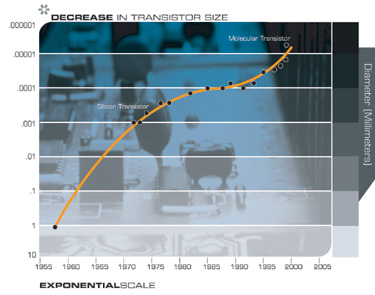
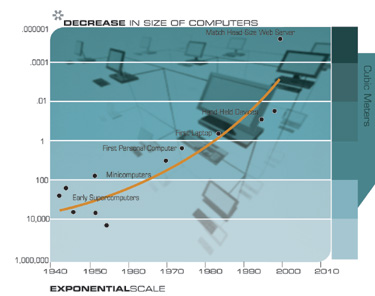
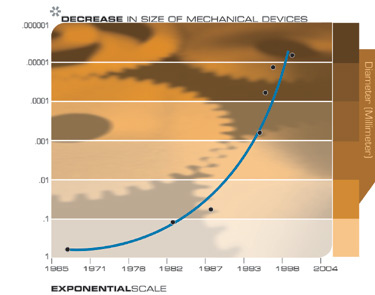
العودة إلى النمو الهائل للحوسبة

إذا نظرنا إلى النمو الهائل للحوسبة في المنظور الصحيح ، كواحد من الأمثلة على الانتشار الواسع للنمو الأسي المستند إلى تكنولوجيا المعلومات ، والذي يعد أحد الأمثلة العديدة لقانون تسريع العوائد ، فيمكننا أن نتوقع بثقة استمراره.

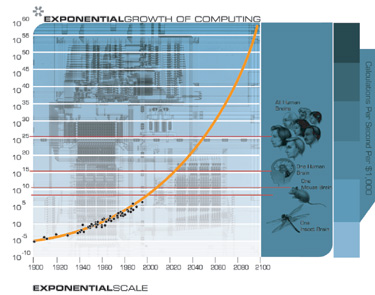
في المربع المصاحب ، أعطي نموذجًا رياضيًا مبسطًا لقانون تسريع العائدات ، من حيث صلته بزيادة الأس (مضاعفة) في قوة الحوسبة. من الصيغ أدناه ، يوضح الرسم البياني أعلاه زيادة مستمرة في سرعة العمليات الحسابية. يتوافق هذا الرسم البياني مع البيانات المتاحة للقرن العشرين ، ويمر بجميع التحولات النموذجية الخمسة ، ويعطي تنبؤات للقرن الحادي والعشرين. يرجى ملاحظة أن معدل النمو يزيد ببطء ، ولكن لا يزال أضعافا مضاعفة.

قانون العائدات المتسارعة فيما يتعلق بنمو الحوسبة

فيما يلي نظرة عامة مختصرة على قانون تسريع العوائد على مثال النمو الأسي المزدوج في السرعة الحسابية. يعتبر هذا النموذج تأثير القوة المتنامية للتكنولوجيا كحافز لتطوير الجيل القادم. على سبيل المثال ، مع أجهزة الكمبيوتر الأكثر قوة ، والتقنيات ذات الصلة ، نكتسب الأدوات والمعرفة لتطوير أجهزة كمبيوتر أكثر قوة ، وجعلها أسرع.

يرجى ملاحظة أن بيانات عام 2000 والفترات اللاحقة تمثل الحسابات في الشبكات العصبية ، لأنه من المتوقع أن يهيمن هذا النوع من الحسابات في نهاية المطاف ، وخاصة عند محاكاة وظائف الدماغ البشري. هذا النوع من الحسابات أقل تكلفة من الحسابات التقليدية (على سبيل المثال ، للحسابات Pentium III / IV) ، مع معامل لا يقل عن 100 (خاصة إذا تم تنفيذها باستخدام الإلكترونيات الرقمية إلى التناظرية ، والتي سوف تتوافق بشكل جيد مع العمليات الكهروكيميائية الرقمية إلى التناظرية للدماغ ). يقابل المعامل 100 حوالي ست سنوات اليوم ، وبعد أقل من ست سنوات في القرن الحادي والعشرين.

تقديري لأداء المخ هو 100 مليار خلية عصبية ، مضروبة في المتوسط ​​ب 1000 وصلة لكل خلية عصبية (تحدث الحسابات بشكل رئيسي في الوصلات) ، ومضاعفة بـ 200 عملية في الثانية. بالطبع ، هذه الدرجات مرتفعة بشكل متحفظ ؛ يمكن العثور على الدرجات العليا والدنيا. ومع ذلك ، فإن الكثير من التقييمات عالية الأداء (أو أقل) تحول التوقعات فقط بعدد قليل نسبياً من السنوات.

بعض التواريخ الأكثر أهمية لهذا التحليل هي:

• نحقق قدرات دماغ بشري واحد (2 × 10 ¹⁶ CPS (حسابات في الثانية)) مقابل 1000 دولار حول 2023.
• نحقق قدرات دماغ بشري واحد (2 × 10 ¹⁶ CPS) في سنت واحد في حوالي عام 2037.
• نحقق قدرات الجنس البشري بأكمله (2 × 10 ²⁶ CPS) مقابل 1000 دولار في حوالي عام 2049.
• نحقق قدرات الجنس البشري بأكمله (2 × 10 ²⁶ CPS) في سنت واحد حوالي 2059.

يحتوي النموذج على المتغيرات التالية:

• الخامس: سرعة (أي الإنتاجية) من العمليات الحسابية (تقاس في الحسابات في الثانية الواحدة ذات الصلة قيمتها)
• W: المعرفة في جميع أنحاء العالم في تصميم وإنشاء أجهزة الحوسبة
• ر: الوقت

يفترض النموذج ما يلي:

• $$$V = C_1 \ cdot W$

بمعنى آخر ، قوة أجهزة الكمبيوتر هي وظيفة خطية لمعرفة كيفية إنشائها. في الواقع ، هذا افتراض محافظ. عادة ، تعمل الابتكارات على تحسين V (أداء الكمبيوتر) عدة مرات ، بدلاً من تحسين مقدارها. الابتكار المستقل يضاعف تأثير بعضهم البعض. على سبيل المثال ، تقنية أشباه الموصلات الجديدة ، مثل CMOS ، وتقنية تخطيط الدوائر المتكاملة الأكثر كفاءة ، وهندسة المعالج المحسنة ، مثل خطوط الأنابيب ، بشكل مستقل وضرب V.

• $$$W = C_2 \ cdot \ int_0 ^ t V$

بمعنى آخر ، W (المعرفة) تراكمية ، والزيادة الفورية للمعرفة تتناسب مع V.

هذا يعطينا:

• $$$W = C_1 \ cdot C_2 \ cdot \ int_0 ^ t W$
• $$$W = C_1 \ cdot C_2 \ cdot _3 ^ {_4 \ cdot t}$
• $$$V = _1 ^ 2 \ cdot _2 \ cdot _3 ^ {_4 \ cdot t}$

تبسيط الثوابت التي نحصل عليها:

• $$$V = C_a \ cdot C_b ^ {C_c \ cdot t}$

وبالتالي ، هذه هي صيغة "التسارع" (أي ، تنمو باطراد) ، تؤدي ، في الواقع ، إلى "قانون مور العادي".

كما ذكرت أعلاه ، فإن البيانات تظهر زيادة هائلة في معدل النمو الأسي. (ضاعفنا القدرة الحاسوبية كل ثلاث سنوات في بداية القرن العشرين ، كل عامين في منتصف القرن ، وكل عام تقريبًا خلال التسعينيات).

دعونا نلقي نظرة على ظاهرة أسي أخرى ، وهي نمو موارد الحوسبة. لا يقتصر الأمر على زيادة قوة كل جهاز من أجهزة الحوسبة (بنفس التكلفة) كدالة لـ W ، ولكن عددهم المستخدم في العمليات الحسابية يزداد أيضًا بشكل كبير.

وبالتالي ، لدينا:

• N: تكاليف الحساب
• $$$V = C_1 \ cdot W$ (كما كان من قبل)
• $$$N = _4 ^ {_5 \ cdot t}$ (التكاليف الحسابية تنمو بمعدل الأسي الخاص بها)
• $$$W = C_2 \ cdot \ int_0 ^ t (N \ cdot V)$

كما كان من قبل ، تتراكم المعرفة العالمية ، وتتناسب الزيادة الفورية مع عدد العمليات الحسابية التي تساوي الموارد المستخدمة في العمليات الحسابية (N) مضروبة في قوة كل جهاز (بتكلفة ثابتة).

هذا يعطينا:

• $$$W = C_1 \ cdot C_2 \ cdot \ int_0 ^ t (C_4 ^ {_5 \ cdot t} \ cdot W)$
• $$$W = C_1 \ cdot C_2 \ cdot (_3 ^ {_6 \ cdot t}) ^ {_7 \ cdot t}$
• $$$V = _1 ^ 2 \ cdot _2 \ cdot (_3 ^ {_6 \ cdot t}) ^ {_7 \ cdot t}$

تبسيط الثوابت ، نحصل على:

• $$$V = C_a \ cdot (C_b ^ {_ \ cdot t}) ^ {C_d \ cdot t}$

هذا منحنى مزدوج الأس ، حيث ينمو معدل النمو الأسي مع سرعته الأسية.

الآن دعونا نلقي نظرة على البيانات الحقيقية. خذ معايير أجهزة الحوسبة الحقيقية وأجهزة الكمبيوتر في القرن العشرين:

• CPS / \ $ 1K: حسابات في الثانية \ 1000 دولار

تتوافق بيانات أجهزة الحوسبة في القرن العشرين مع:

• CPS / \ $ 1K = $$$10 ^ {6،00 \ cdot \ frac {20،40} {6،00} ^ {\ frac {Year-1900} {100}} - 11،00}$

يمكننا تحديد معدل النمو خلال فترة زمنية:

• معدل النمو =$$ $ inline $ 10 ^ {\ frac {\ log (CPS / \ $ 1K لـ \ hspace 5mu الحالي \ hspace 5mu year) - \ log (CPS / \ $ 1K for \ hspace 5mu السابقة \ hspace 5mu year}} {current \ hspace 5mu year - السابقة \ hspace 5mu year}} $ inline $
• الدماغ البشري = 100 مليار (10 ¹¹ ) خلية عصبية × 1000 (10 ³ ) اتصالات لكل خلية عصبية × 200 (2 × 10 ² ) حسابات في الثانية الواحدة لكل اتصال = 2 × 10 ^{16 عملية} حسابية في الثانية
• الجنس البشري = 10 مليارات (10 ¹⁰ ) أشخاص = 2 × 10 ²⁶ حساب في الثانية

هذه الصيغ تعطي الرسوم البيانية أعلاه.

بالفعل ، من المتوقع أن يكون حاسوب IBM Blue Gene العملاق ، الذي من المقرر أن يكتمل بحلول عام 2005 ، قادرًا على أداء مليون عملية في الثانية (أي مليار ميجافلوبس أو بيتافلوبس واحد). هذا هو بالفعل واحد من عشرون إنتاجية الدماغ البشري ، والتي أقدرها بشكل متحفظ بنحو 20 مليون عملية في الثانية (100 مليار خلية لكل 1000 خلية لكل خلية عصبية بمعدل 200 عملية حسابية في الثانية لكل اتصال). , 2010 , 2020 . 2030 ( ), , $1000. 2050 , $1000 , . , , . , , , ( ) . , . , . , . , , , , 200 - .

. . , , , . , , . , , , , , . , . — , .

, , , , . , . , , , , . , . , , . . -, .

— . , , . , ( , , ). , , , ; . , , .

, , . , . , .

, , , . , , , . « », , , . , . , , , . — , , , . , , , , , ( , — ).

— « » , . , , . , , ( ) . , , .

— : , , , , . , .

. , 10 http://www.nlm.nih.gov/research/visible/visible_human.html .

25 — , , . , , , .

, , , , , . (Andreas Nowatzyk) - (Carnegie Mellon University) 200 , , .

, - () , , , , , . , — , . , .

, . , , , , , . , , . , . , , , , .

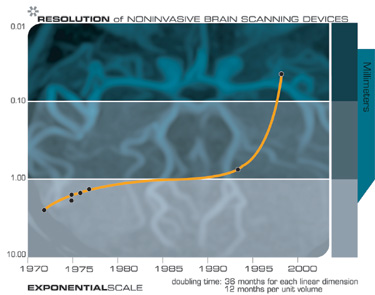
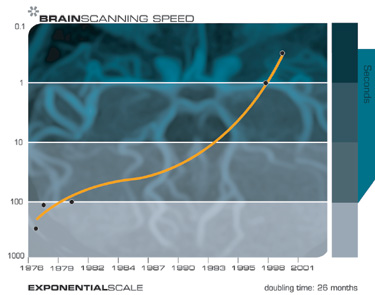
, — . 2030 «» ( ) , . — , , . . , , , ( , ).

, . , , , . , . . , , . , , , 2030 . - , , .

, ? , , . . . , , ( 100 , 1000 , ), , , .

, , , .. Microsoft Word. , , ( ). , - . , , . , .

. , , (Lloyd Watts — www.lloydwatts.com ) , . . , , , . , , . , (Hans Moravec) , 1000 , .

:

(Cochlea): . 30000 - .

. (MC — Multipolar Cells): .

. (GBC — Globular Bushy Cells): .

(Olivary Complex) ( ( LSO MSO)). .

. (SBC — Spherical Bushy Cells): , , .

. (OC — Octopus Cells): .

. (DCN — Dorsal Cochlear Nucleus): .

(VNTB — Ventral Nucleus of the Trapezoid Body): , .

, (VNLL — Ventral Nucleus of the Lateral Lemniscus, PON — Peri-Olivary Nuclei): .

(MSO — Medial Superior Olive): ( , , ).

(LSO — Lateral Superior Olive): .

(ICC — Central Nucleus of the Inferior Colliculus): .

(ICX — Exterior Nucleus of the Inferior Colliculus): .

(SC — Superior Colliculus): .

(MGB — Medial Geniculate Body):

(LS — Limbic System): , , , ..

(AC — Auditory Cortex)

— «Tabula Rasa» ( ), . « », , . , , .

, - , , . , , , . , .

, ---- -, ----. - , , , , , , . , , .

, . , . , , , , .

, , , . , (Ted Berger) Hedco Neurosciences , , . (Carver Mead) (CalTech) , - .

- (San Diego's Institute for Nonlinear Science) . ( - ) , « ». , , . ( ), , , . , , , , «». «» «» . (, , ), «» .

, - , . , - ( , «») , , . , . , .

, , . . , , , . — , .

, ( , ) , , . , , , , .

?

?

, «». , , . (, , ) . , , . , , .

, , ( ), . , — , , . , , . , , . , .

, . , , , «», . , , , , . — , , , . , , , - .

. « » (.. ), , «» . , ( ), , - .

, , , , , . , , .

, . «» , , . , - , «» , , , . , . , . , , .

. , , , . , . , , . , , .

, , : .

, , , , , . , , , , , : , , , , . , . , . .

, : , (.. ), ( ), , ..

. , ( ), . , ( ) , .

?

, : , , ? «» ? ?

. . , , , , - . (Marvin Minsky) , « - . , ».

, , . , , , ? , , ? , , , , ?

. «, », ? , , , , , .

, : « , , .» ?

, , , , ( ), ?

, ? , . , , . , — , — , , , , ( ) , , , , «» — ( ) , , , . : « , -, , , , , . , .

-!

? , ( ) . , . , , , .