دليل الرياضيات قصيرة للأجانب

ما هو عليه

وكيف يمكن للمرء أن يشكل المواد المطلوبة للدورات الأولى للجامعة في المرحلة الرابعة مع النفور من الجبر؟

لجنون الشجعان نغني أغنية!

الجمهور المستهدف من الدليل هو أولئك الذين يهتمون فجأة بالرياضيات أو يشعرون بالحاجة إلى زيادة فعاليتهم المهنية ، لكنهم لسبب ما لا يستطيعون تكريس عدة سنوات من حياتهم للتعليم الأكاديمي. إذا كنت بحاجة إلى فهم ، ولكن المعرفة الأساسية غير موجودة بشكل كبير ، وكنت تشعر أنك أجنبي في بلد الرياضيات ، حيث يتحدثون لغة غير مفهومة ، حاول أن تسير بهذه الطريقة كسائح. المسار بأكمله عبارة عن جولة لمشاهدة معالم المدينة ، وهو مصمم لعدة أيام ، بحد أقصى أسبوعين. للمقارنة: دورة دراسية كاملة حوالي خمس سنوات. الهدف النهائي للمسار المقترح هو التعرف على مبادئ قسم متخصص للغاية - التشفير الإهليلجي. ومع ذلك ، ليس من الضروري الانتقال إلى النهاية إذا كان هذا القسم يقع خارج نطاق اهتماماتك أو إذا كنت تواجه صعوبات أو أخطار خطيرة. ولكن ، نظرًا لأنك التقطت "الدليل" ، ما زلت تحاول الوصول إلى نهاية قسم "لغة الصيغة" على الأقل.

مثل القاموس ، يمكن أيضًا استخدام هذا الدليل للترجمة العكسية. ربما سيكون من المفيد لعلماء الرياضيات الذين يضطرون للاتصال والعمل عن كثب مع غير علماء الرياضيات ، والتغلب باستمرار على فجوة سوء الفهم. هذه الحالة تبدو صعبة للغاية لدرجة أن خط مكسيم غوركي في الرسم هو إجابة عالمية لكلا الجانبين. في أي حال ، آمل أن أحصل على تعليقات وأحاول أن أجدد معرفتنا حول سبب عدم فهمنا لنا ، وكيف يمكن إصلاح ذلك.

والآن ، مع العلم أنه لا توجد طرق ملكية هنا ، سنحاول تمهيد مسار سياحي على الأقل.

لغة الصيغة

قيل لي أن كل صيغة مدرجة في الكتاب ستخفض عدد العملاء إلى النصف. ثم قررت الاستغناء عن الصيغ على الإطلاق. صحيح ، في النهاية ما زلت أكتب معادلة واحدة - معادلة آينشتاين الشهيرة E = mc ^ 2. آمل ألا يخيف نصف القراء المحتملين.
ستيفن هوكينج - تاريخ موجز للوقت

إذا كان ناشر Hawking على حق ، فإن إضافة 33 صيغة فقط يكفي لجعل عدد القراء المحتملين قريبًا من الصفر. هل سنحاول؟

بادئ ذي بدء ، من الضروري تحقيق مستوى كاف من فهم الترميز. تذكر ، الرياضيات هي لغة.

في التقريب الأول ، يمكن التمييز بين عدة طبقات لفهم النص الرياضي. الطبقة الأولى هي اختيار المعجم ، وهو ما يسمى التحليل المعجمي. والثاني هو بناء التعبيرات وغيرها من المنشآت الدلالية. يسمي المبرمجون هذه الكلمة "تحليل" ، أي "التحليل" ، وعادة ما لا يصفها علماء الرياضيات العامة على الإطلاق ، لأنهم يستخدمون هذه الآلية دون وعي. فيما يلي الطبقات المسؤولة عن فهم مجال الموضوع والمعنى المادي وكل ذلك.

يرى بعض علماء الرياضيات المبرمجين غير علماء الرياضيات. هذا غير عادل. أولاً ، يتعين على المبرمجين التعامل مع آلة لا تغفر الإغفالات في نص البرامج. قارن مع مقال علمي نموذجي ، حيث غالبًا ما تستخدم التعبيرات "واضحة" ، "سهلة العرض" ، "لا تفكر" ، وما إلى ذلك ، لكن في الواقع فإن التحولات ليست واضحة تمامًا. لذلك ، وبفضل البرمجة ، ولدت مجموعة كاملة من الرياضيات مكرسة للغات رسمية وتحليلها. ثانياً ، في ظروف قاسية ، تطورت لغات البرمجة نفسها والأدوات ذات الصلة. تعرف على كيفية حل اللغات الحديثة بأناقة لمشكلة مطابقة المتغيرات مع الكائنات. بالمناسبة ، تتمثل المشكلة الخطيرة في عدم الخلط في التدوين عندما يكون هناك الكثير منهم ، وهم يأتون من مصادر مختلفة. وإذا كنت تقضي بعض الوقت في نظرة عامة سريعة على لغات محددة مثل Coq و Agda و Idris ، فسترى أقرب صلة بين الرياضيات والبرمجة نفسها.

تحليل معجمي

اعتدت أن أعرف كيف تتم كتابة الرسائل ، كنت أؤمن بقوة الكلمات.
محرقة - آخر فرصة

أولاً ، اسأل صديقًا مبرمجًا عن ماهية اللغوي والمحلل اللغوي. لا تحتاج إلى التعمق ، فقط افهم من خلال الأمثلة ما هو الرمز المميز. إذا سمعت كلمات غريبة مثل "el-er-parser" أو "شجرة بناء الجملة" ، فاترك الغرفة بهدوء. على الأرجح ، لديك بالفعل ما يكفي ، لم يعد هناك حاجة للمبرمج. هضم علمك. ثم تحتاج إلى معرفة كيفية التمييز بين الرموز في النصوص الرياضية الحقيقية. تدرب على المقالات التي تم تنزيلها بشكل عشوائي. تجنب المستندات بتنسيقات غير pdf ، وكذلك النصوص الموضوعة على صفحات الويب مباشرةً. ومع ذلك ، هناك مواقع يُعرف عنها بشكل موثوق أنه يمكنها عرض النصوص الرياضية بشكل صحيح (يتم تضمين ويكيبيديا وحبر في القائمة البيضاء). الكتب الورقية هي أيضا مناسبة عموما. لا تحاول استخراج المعنى من النصوص الموجودة ، فقط تدريب على تحليل الصيغ.

رسائل

• عادة ما يتم استخدام الحروف من اثنين من الحروف الأبجدية - اللاتينية واليونانية ، ولكن في بعض الأحيان يتم العثور على الحروف السيريلية والعبرية. يحدث أن الحروف من الحروف الهجائية المختلفة تتزامن في الاسلوب. على الرسالة ، هذا لا يسبب مشاكل ، حيث لا يتم استخدام حرفين مختلفين من نفس النوع في نفس النص. ومع ذلك ، قد تصادف سخرية علماء الرياضيات إذا ، على سبيل المثال ، قرأت B بصوت عالٍ كـ "be" عندما تعني "beta". كن مستعدا نفسيا لهذا ، عليك أن تتحمل.
• الأحرف الكبيرة والصغيرة تمثل كائنات مختلفة. (بالنسبة للبعض ، يبدو هذا واضحًا جدًا ، ولكني أعتبر أنه من الضروري نطقه صراحة. بمجرد أن أحتاج إلى تقديم جوهر عملي إلى زملائي من قسم براءات الاختراع. عندما وصلت تقريباً إلى طابع الحكاية "أبي ، أين البحر؟" ، أدركت فجأة أن الفتيات يعتبرن تعييناتي m و M للإشارة إلى نفس الشيء ، وبمجرد أن يتم إزالة سوء الفهم ، فإن العملية برمتها ، بفضل احترافهم المهني في عملهم ، قد انتهت بسرعة وبشكل حاسم بنجاح كامل.)
• الحرف نفسه ، المكتوب في خطوط مختلفة ، يعني كائنات مختلفة.

كقاعدة (في الجبر) ، حرف واحد هو رمز مستقل. إذا تم كتابة العديد من الحروف في صف واحد ، فإن الضرب يكون ضمنيًا. على سبيل المثال ، تعني كلمة abc منتج a و b و c. ومع ذلك ، هناك استثناءات. بادئ ذي بدء ، هذا هو اسم العديد من الوظائف القياسية وغيرها من الرموز ، وهو رمز مميز متعدد الحروف: $$$\ sin ، \ cos ، \ min ، \ max ، \ sup ، \ lim$ إلخ عادة ما يتم تصويرها بأسلوب مستقيم (روماني) ، على عكس الرموز الأخرى للحروف المكتوبة بالخط المائل. بالإضافة إلى ذلك ، في علوم الكمبيوتر وفي بعض المناطق الأخرى ، ينطلقون من هذه القاعدة ، حيث تشير سلسلة من الحروف إلى رمز كلمة واحد. إذا كان هناك أدنى شك في حالة معينة ، فاستشر أخصائيًا.

بين قوسين

يتم لعب الدور الأكثر أهمية من حيث التحليل بواسطة الأقواس. ربما تعلم بالفعل أو تخمن أن الأقواس تُستخدم لتجميع الرموز المميزة. ولكن هناك استثناءات. إذا كانت الصيغة تبدو غريبة بالنسبة لك وتحتوي على أزواج إضافية من الأقواس ، أو حتى توازن الأقواس مكسور ، فمن المحتمل أن تصادف مثالًا مع استخدام بديل للأقواس. الذهاب إلى متخصص للتوضيح.

مؤشرات

انتبه للمؤشرات العلوية والسفلية. هذا هو الشكل الذي تبدو عليه الكتابة الفوقية والمنخفضة. النص المرن أبسط: كقاعدة عامة ، فهو يرمز إلى الأس. مع الجزء السفلي أصعب قليلا. يمكن فهمه بطريقتين:

• مثل عملية رسم الخرائط. على سبيل المثال $$$x_i$ هل هذه وظيفة $$$x$ الذي يأخذ كحجة $$$i$ . إذا لم تكن هذه النقطة واضحة الآن ، فلا بأس ، يمكن تخطي هذا المكان في الوقت الحالي.
• كوسيلة لتشكيل رمز مميز جديد عند انتهاء الحروف المريحة بالفعل. غالبا ما يمكن افتراض ذلك $$$a_1 ، a_2 ، a_i$ - هذه ليست سوى ثلاثة أشياء مختلفة.

في مرحلة ما ، قد يبدو لك أن هاتين النقطتين هما نفس الشيء في الأساس. لا تقلق ، هذا أمر طبيعي ، لقد أصبحت أقرب قليلاً إلى التنوير. جدولة اجتماع مع متخصص.

شخصيات أخرى

علماء الرياضيات هي جماليات. انهم يحبون عندما المحتوى ليس فقط ولكن أيضا شكل جميل. انهم سعداء عندما تتم كتابة الصيغ في الطباعة جيدة ومناسبة. قدم كنوت خبز الزنجبيل لذيذ دعا $$$\ TeX$ . خذ برنامجًا تعليميًا عن كتابة الصيغ وتنضيدها وابحث عن جداول الرموز هناك. من المهم الآن بالنسبة لك كيفية تصنيف هذه الرموز: الحروف ، العوامل ، علامات العلاقة ، الأسهم ... دون الخوض في المعنى الرياضي للرموز ، حاول أن تفهم كيف يتم استخدام رموز كل فئة بشكل نحوي. على سبيل المثال ، هناك فئة من العمليات الثنائية التي يجب أن يكون نوعها من التعبير الفرعي الأيمن والأيسر على قدم المساواة من رمز العملية.

الأرقام

غير علماء الرياضيات يعتقدون أن علماء الرياضيات يعتقدون. في الواقع ، نادراً ما يتم اعتبار علماء الرياضيات ، ويتم استخدام الأرقام بشكل أساسي في كائنات الترقيم. على ما يبدو ، لذلك ، تمت إضافة قسم "الأرقام" في عجلة من أمره ويتبع قسم "الرموز الأخرى" بطريقة غير منطقية. يمكنك أنت أن تخبر الخبراء كيف تتشكل الرموز الرقمية وماذا تعني.

اتفاقيات التدوين

دع a ، b ، c ، d ، e ، f أرقامًا حقيقية ، حيث e لا تساوي بالضرورة قاعدة اللوغاريتمات الطبيعية ، على الرغم من أنها قد تتزامن معها.

في الرياضيات ، هناك اصطلاحات حول أي الشخصيات لاستخدامها في أي الحالات. ومع ذلك ، في أقسام مختلفة قد تختلف هذه الاتفاقات. هو مثل لهجات اللغة. هناك تدوينات موحدة في جميع الرياضيات. تحقق من الاتفاقيات المقبولة في مجال الموضوع الخاص بك. بالإضافة إلى ذلك ، فإن بعض العلماء يهملون وينتهكون أحيانًا الاتفاقيات المقبولة عمومًا. لسوء الحظ ، في معظم الحالات لا توجد مجموعات من القواعد حول هذا الموضوع ، يمكنك مناقشة هذا الأمر مع أخصائيك في بعض الأحيان.

على الرغم من أن الرياضيات تتجاوز الحدود الوطنية عمومًا ، إلا أن هناك اختلافات ثقافية. قد تصادفهم إذا انحرفت عن المسار الذي اقترحه الدليل. على سبيل المثال ، يتم التمييز بين التعيينات الإنجليزية والروسية للوظائف المماسية ، والشفافية ، الزائدية. أيضا ، يمكن نطق الحروف نفسها بشكل مختلف اعتمادا على التقاليد الثقافية. لتوفير الجهد ، وتعلم أسماء الإنجليزية من جميع الحروف ، بما في ذلك اليونانية. إذا لم تكن قد تخطيت المدرسة ، فلن تكون هناك على الأقل مشكلة في الأبجدية اللاتينية. إذا كنت تستخدمها باللغة الروسية ، فقد يتكلم المحاورون معك ، ولكن هذه المرة سيكون عليهم تحملها. إذا كنت تريد أن تجعلهم سعداء ، وتعلم أسماء الحروف اللاتينية واليونانية مقبولة في الثقافة الرياضية الناطقة باللغة الروسية.

إعراب

التعبيرات

من المرجح أنك سمعت مصطلح "شجرة" ليس في علم النبات ، ولكن بالمعنى الرياضي. هذا شيء بسيط إلى حد ما ، إذا لزم الأمر ، تحديث علمك. لذلك ، فإن التعبير الرياضي له بنية شجرة. هذا يعني أن التعبير يتكون من تعبيرات فرعية تتكون من تعبيرات فرعية ... لكن هذه العملية لا تنتهي ، ولكنها تنتهي ببعض التعابير الفرعية التي تتكون من الرموز.

بعض الرموز نفسها عبارة عن تعبيرات أولية. على سبيل المثال ، الأرقام (بشكل أكثر دقة ، حرفية رقمية) والمتغيرات. ويتطلب البعض إضافة الحجج إليهم في مواقف معينة ، أي نوع من التعبير الفرعي. ثم يشكلون تعبيرًا أكبر. على سبيل المثال ، يتطلب رمز عملية الإضافة التعبيرات إلى يمينها ويسارها. يمكننا أن نقول أن اللغز يحتوي على بعض التكافؤ ، أو إذا كنت تفضل الكيمياء ، فإن التكافؤ ، هو كم وفي أي مكان تحتاج إلى إضافته إلى معجم التعبير الفرعي لتكوين تعبير. للتشغيل + arity يمكن وصفها على النحو التالي: $$$\ cdot + \ cdot$

يعني هذا الإدخال تمامًا أن الرمز المميز + يتطلب وسيطات إلى يمينه ويمينه. تتطلب الرموز المختلفة عددًا مختلفًا من الوسائط ، بالإضافة إلى أن موقع الوسائط لا يقتصر على "اليمين" و "اليسار" ، ولكن يمكن أن يكون ، على سبيل المثال ، "أعلى" ، "أسفل" ، "أسفل اليمين". هناك أيضًا رموز مركبة موجودة منذ العصور القديمة ، ولكن mixfixes حصلت على اسم خاص مع تطور لغات البرمجة. على سبيل المثال ، يتم الإشارة إلى المنتج القياسي للناقلات كما يلي: $$$\ langle \ cdot ، \ cdot \ rangle$ .

الرموز في بعض الأحيان تتعارض لأنهم لا يستطيعون تحديد من تنتمي الحجة المكتوبة بينهما. ثم عليك أن تضيف الأقواس.

المتغيرات

بعض الرموز لها معنى ينسب إليها من الأعلى - إما في مكان أعلى في النص ، أو عن طريق روابط في نصوص أخرى. أو المعنى الضمني مقبول بشكل عام في تخصص معين أو في جميع الرياضيات. على سبيل المثال ، يشير الرمز الإضافي إلى عملية إضافة. زائد - هو في أفريقيا زائد. ومع ذلك ، ربما في مكان ما أقرب إلى نهاية مسارك ، ستجد رمزًا زائدًا مع بعض المعنى غير العادي. لا تزال هناك رموز (عادةً ما تكون أبجدية) لا يشار إليها صراحة بأي شيء ، يطلق عليها اسم المتغيرات ، والتي يوجد منها عدة أنواع.

• الخيار. هذا متغير يقال عنه أنه يدل على شيء ما ، لكنه لا يقال بالضبط. إذا بدا الأمر غريباً بالنسبة لك ، فيمكنك تخطيها الآن ، وعندما تتوافق مع المعلمات ، ستفهم على الفور كل شيء مع أمثلة.
• متغير حر. إذا تم العثور على متغير في التعبير عن أي شيء يقال ، ثم يسمى هذا المتغير مجانا. بالمعنى الدقيق للكلمة ، لا شيء على الإطلاق يمكن أن يقال. لديك الحق في أن تطلب من مؤلف الصيغة التي تم تعيين المتغير الحر فيها. لا تتردد في طرح السؤال ، وهذا مفيد: حتى لو تبين أن التفسيرات غير مفهومة ، فسوف تأخذك على محمل الجد.
• المتغير المنضم. إذا كنت لا تحب تحرير المتغيرات الحرة ، فهناك عدة طرق للحد من حريتها. يمكنك إضافة شيء ما إلى التعبير ، بحيث تحصل على تعبير جديد يتم فيه تأمين المتغير المجاني السابق. والتعبير الجديد ، على عكس القديم ، لن يعتمد على هذا المتغير. إذا كنت مهتمًا بماهية هذا "الشيء" ، فقم بإلقاء نظرة على الكميات أو على جزء لا يتجزأ منه. حاول أن تنظر فقط إلى بناء الجملة ، وليس الخوض في المعنى ، ولكن ، كما تعلمون ، تسبب الإدمان.

السياق

يحدث ، بالنظر إلى الصيغة ، أنه من المستحيل التمييز بين المتغير الحر من المعلمة. وهذا يعني أن هناك حاجة إلى الحصول على معلومات إضافية من السياق ، والتي يتم التعبير عنها عادةً بواسطة صيغ أو نصوص أخرى باللغة البشرية. اعتمادًا على السياق ، قد يكون للصيغة معاني مختلفة. إذا كنت بحاجة إلى فهم الصيغة ، فقم دائمًا بدراسة السياق والبحث عن الفهم.

ومع ذلك ، يمكن أن توجد الصيغ بدون سياق ، ببساطة ككائن نحوي يمكن إجراء التحويلات عليه. غالبًا ما يستطيع علماء الرياضيات تعميم - "نسيان" السياق ، ثم إجراء الحسابات ، ثم "تذكر" السياق وإعادة فهم معنى الصيغ التي تم الحصول عليها.

يساوي الرمز

علامة المساواة مهم جدا. يتم استخدامه بطرق مختلفة ، ويجب أن تكون قادرًا على التمييز بينها.

• تقييم المتغير من حيث القيمة. هذا هو عندما يكون المتغير على اليسار ويكون التعبير على اليمين. في بعض التخصصات ، في مثل هذه الحالات ، بدلاً من = يكتبون: = أو حتى :: =.
• الهوية. على اليسار وعلى اليمين بعض التعبيرات ، ويدعي الشخص الذي كتب هذا أن كلا التعبيرين متساويان. يستخدم الرمز أيضًا هنا. $$$\ equiv$ . هل فكرت في ماذا تعني "المساواة"؟ الأمر يستحق المناقشة ، ولكنه قد يأخذك بعيدًا عن الطريق.
• المعادلة. هذه طريقة لوصف الكيانات الجديدة بشكل أساسي. يقوم علماء الرياضيات بذلك على هذا النحو: فهم يأخذون العديد من المتغيرات الحرة ، ويبنون التعبيرات عليها ويقودونها إلى معادلة أو حتى إلى نظام من عدة معادلات ، بحيث يكونون أقرب. ثم يراقبون كيف تتعجل هذه المتغيرات المؤسفة في القيود ، وتشكل مجموعات غريبة. ثم يدرسون هذه المجموعات باهتمام كبير. (بالمناسبة ، يمر طريقك عبر منطقة نظرية المجموعة ، يجب عليك التعرف عليها بشكل أفضل.) لوصف المجموعة التي تم الحصول عليها هي حل المعادلة. يحصل الأطفال في المدرسة عادة على معادلات تؤدي إلى مجموعات بسيطة جدًا من عنصر واحد ، وأحيانًا اثنين أو لا شيء. لكن العلماء البالغين في هذه المسألة هم كبار الفنانين. وبعض الفيزيائيين قادرون على توليد الكون بأسره بمعادلة واحدة.

استخراج المعنى من الصيغ

هناك شيء مكتوب ، ولكن بين قوسين OH. لقد حاولوا - وحقا يا OH.

. . ?

, . , . , , ́, ́, ́ ́. : , . , , . , - , , , — , , , .

, , . .

- , - , . . , «- », : « », «», « », « » ..

, , , …
—

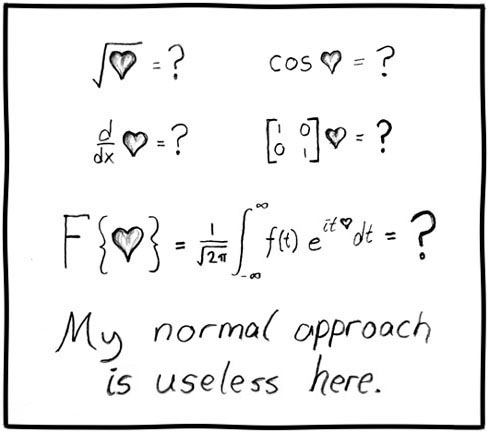
XOR , ?

, . .

, , , . , . , , , , , , .

- , from. , , , , , . , .

, . — ( ), , . , , , . , .

, . , , . , , , .

, , - - . - (, computer science) . , .

— . — .
, -

, . , , . . .

, . . , . , . , , - , . « ». , . , . « ?».

, . $$$a^b$ . : a — , b — , , , . : , .

, .

. «», « » « », . , , . , . , , . , , . , . . : $$$\infty$ . , — . . : ! ! - , , . — , .

• . . .
• . . , ? -.
• . , . -, , , .
• . . , - - .
• , « ». , . , . , .
• , . , . , , .

بالعودة إلى صندوق الحماية للمجموعات المحدودة ، تحقق مرة أخرى من مدى تذكرك للرمز. العب مع مجموعات محدودة من الأحجام الصغيرة. حاول تطبيق العمليات الأساسية عليها. بناء العديد من المجموعات الفرعية. إذا نسيت ما هو الاعتراض ، فقم بتجديد معلوماتك في الكتب المدرسية لمرحلة ما قبل المدرسة. بعد كل شيء ، كنت تعرف هذا المفهوم من فترة ما قبل الكلام ، وبعد ذلك فقط لم يطلق عليه في أي حال ، أليس كذلك؟ تأكد من الحدس الخاص بك في وئام تام مع التعاريف والبيانات الأساسية. إذا لم يكن الأمر كذلك ، فاتصل بأخصائي.

قبل المغادرة ، انظر حولك مرة أخرى. على حافة الصندوق الرملي ، يمكنك رؤية زاوية من المتناهية الصغر. كل شيء بسيط معهم. قل مرحباً لهم ، لا تقل أنك ذهبت خارج صندوق الرمال.

مرة أخرى عن التدوين

كم هو صعب العيش بين الناس المملين
وقال مايكل البالغ من العمر ثلاث سنوات
بين المملون
تصحيح ايجور ، وثلاثين وارتداء النظارات

مجموعات Abelian -> الفضاء الخطي -> العوامل -> الوظيفية في الفضاء الخطي. ولكن بعد تنزيل هذا الفرع ، يمكنك تشغيل كلمة "وظيفية" في وصف وظيفة البرنامج.

أنت تعرف بالفعل بعض المصطلحات الرياضية وستستمر في معرفة المزيد. حاول عدم استخدامها دون جدوى عند التواصل مع المتخصصين في الموضوعات ذات الصلة. على سبيل المثال ، بدلاً من عبارة "مجموعة من الأساليب" ، فقط في حالة ، من الأفضل أن تقول "مجموعة من الأساليب" أو "مجموعة من الأساليب" حتى لا يظن أحد أنك قد قمت ببناء عملية على مجموعة من الطرق تلبي بديهيات المجموعة. إذا كنت تفتقد الكلمات الشائعة أثناء التواصل غير الرسمي حول الموضوعات الرياضية بسبب حقيقة أنها تجد نفسها مشغولة بالمصطلحات ، فمن الأفضل استخدام ما يسمى بمتغيرات metasyntactic: "garbage" ، "crap" ، "shnyaga" ، وما إلى ذلك. الطلاء مع الصفات: "الخرقاء" ، "السلس" ، "غث". لا يبدو ذكيًا جدًا ، لكن من المرجح أن تفهمه. بعد مرور بعض الوقت ، سوف تتخلص من الكلمات البديلة القبيحة ، ولن يتسبب خطابك في ألم علماء الفلك أو علماء الرياضيات.

لا تستخدم الكمي العالمي دون جدوى. يتم تمثيل مقاييس الشمولية المعبر عنها باللغة العادية بالكلمات "دائمًا" و "الكل" و "الكل" و "الجميع" و "أي" وما إلى ذلك. عبارة "أبدا" ، "لا مكان" ، إلخ. إنهم يمثلون أيضًا هذا الكمي ، ولكن مع النفي ، يعني "أبدًا" يعني "لا دائمًا". غالبًا ما يفسر علماء الرياضيات البيانات باستخدام المقياس الكمي العالمي حرفيًا ، وبعد ذلك ، بعد تقديم مثال مضاد ، يثبتون خطأكم الرسمي. لا تحتاج إلى ضغط إضافي؟ بالطبع ، هناك حالات يمكن فيها استخدام المقياس الكمي العالمي ويجب استخدامه.

في الرياضيات ، غالبًا ما يكون هناك تجانس. هذا عندما تحدد كلمة أو رمز واحد عدة مفاهيم مختلفة تمامًا. أولاً ، يعزى ذلك إلى عدم وجود كلمات وشخصيات جيدة. ثانياً ، على عكس اللغات الطبيعية ، غالبًا ما تتحول المفاهيم المختلفة بعد التعميم إلى نفس الشيء. علماء الرياضيات الذين يلاحظون أن هذا هو نفسه كما في كثير من الأحيان تجربة النشوة الدماغية من هذا الوعي. تنشأ الأحاسيس القوية بشكل خاص إذا كان الباحث قد قام بجزء مهم من الطريق إلى الوعي بمفرده. من الممكن أن تواجه أيضًا نفس الأحاسيس القوية. لكن إذا لم يكن كذلك ، فلا بأس ، هذا جيد أيضًا. لا تتردد في مشاركة مشاعرك مع الخبراء.

عادةً ما لا تجعل homonymy من الصعب فهمه ، لأن علماء الرياضيات يتأكدون بعناية من أن جميع التعاريف دقيقة وصحيحة.

منطق

عليك أن تعمل بشكل حصري تقريبا مع الأشياء النهائية. هذا يعني أن أفكارك البديهية حول المنطق كافية على الأرجح ، والأهم من ذلك ، لن تؤدي إلى تناقضات. فقط في الحالة ، اقرأ عن pusens modus ، حتى لو لم يكن الاسم مألوفًا بالنسبة لك ، فأنت تعرف بالتأكيد الجوهر.

بشكل عام ، فإن المنطق يدور حول كيفية إصدار بيانات جديدة بناءً على البيانات الحالية. ألقِ نظرة حولك. في كل مكان حولك أقوال: كبيرة ، صغيرة ، واضحة ، غير مفهومة. يمكنك افتراض أن البيانات مقسمة إلى نوعين: صواب وكاذب. وهنا التماثيل! كيف تحب ذلك؟

$$

$$\ int e ^ x = f (u_n)$$

هذا البيان ليس صحيحًا أو خاطئًا ، فهو لا معنى له (على الأقل من وجهة نظر الرياضيات) ، لأن ما يُكتب على يسار علامة المساواة ليس تعبيرًا. يمكنك إضافة dx إلى جزء لا يتجزأ ، ولكن بعد ذلك تبقى عدة متغيرات حرة ، وبسبب هذا التعبير ليس عبارة. يجب أن تعني شيئًا ما أو تجعلهم متصلين ، حتى نتمكن من التحدث عن الحقيقة.

حسنًا ، دعنا نفكر فقط في عبارات ذات معنى. يجب أن تكون إما صحيحة أو خاطئة؟ اتضح ، لا. بعض العبارات لا يمكن إثباتها أو دحضها ، فهي تسمى غير قابلة للحل. من غير المحتمل أن تتم مواجهة الملاحظات غير القابلة للحل في طريقك. ومع ذلك ، فإنهم بالتأكيد سيصادفون تلك الحقيقة التي لا يعرفها حتى الآن أي من الأشخاص الأحياء.

إذا لم تطيع آخر مرة ونظرت إلى هاوية أسس الرياضيات ، فمن المحتمل أن تلاحظ أن هناك أكثر من منطق واحد ، وأن هناك العديد من الأسباب المختلفة. لحسن الحظ ، لن تكون هناك حاجة لهذه المعرفة ، التي تولد الكثير من الأحزان. إذا كنت تشعر بالراحة للاعتقاد بأن الحقيقة هي نفسها دائمًا ، استمر في التفكير بذلك.

نظرية الفئة

"ديوكسيريبونوكليتيك ،" قلت. - هذا مثل هذا الحمض. النووي الريبي منقوص الأكسجين.
ابتسم بائسة ، وضبط نظيره النيز.
"حمض" ، كرر بصوت اعترض. "لماذا هي هكذا؟"
قلت تعاطفًا: "لا يمكنك الاتصال بها بطريقة أخرى". "ما لم يختصر الحمض النووي." نعم ، أفتقدك ، فديا ، تابع القراءة.
"نعم ، نعم ،" قال. "أنا أفضل أن أفتقدها."
أركادي وبوريس ستروغاتسكي - حكاية الثلاثة

على الرغم من أن نظرية الفئة بحد ذاتها خطيرة مثل نظرية المجموعات ، إلا أننا نحتاج إلى استخلاص بضعة مفاهيم ترتبط رسميًا بهذا القسم.

• الطبقات المجاورة. هذه هي واحدة من الطرق لبناء هياكل جديدة من تلك القائمة. اقرأ التعريف ، انظر بعض الأمثلة. إذا لم تكن واضحة ، يمكنك تخطي. ولكن إذا كنت لا تزال تخترق ، فسوف تحصل على بعض المكافآت لفهم أشياء أخرى. على سبيل المثال ، عن الحلبة $$$\ mathbb {Z} _n$ (ستكون هناك حاجة لهذا الشيء بعد ذلك بقليل) من المريح التفكير كفئة من الاستقطاعات ، وليس كنتيجة لعملية أخذ بقية التقسيم. أيضًا ، سيبدو التعريف المدرسي للناقلات كقطعة ذات سهم مثير للسخرية وحتى خاطئًا بالنسبة لك. يمكنك تعليم أصدقائك أن المتجه ليس جزءًا ، لكنه فئة من الشرائح.
• Morphisms. التشكل هو بعض العلاقة بين زوج من الأشياء. أنت تعرف نوعًا واحدًا من المورفولوجية منذ حوالي الثالثة من عمره - وهذا يمثل انحرافًا بين مجموعات محدودة. قراءة تعريف التماثل وإدراك أن هذه هي حالة عامة أكثر من bijection. الحصول على فهم جيد ، وهذا هو المهم. إذا لزم الأمر ، استشر أخصائي. علاوة على ذلك يمكنك أن تقرأ عن التجانس (لا ينبغي الخلط بينه والتماثل!). إذا كان هناك رهاب المثلية أو صعوبات أخرى ، يمكنك تخطي.

بشكل عام ، فإن نظرية الفئات بأكملها هي أكثر أقسام الرياضيات تجريدًا ؛ لا يوجد شيء سوى الأشياء الصغيرة والسهام. على الرغم من بعض الخطر على النفس ، يمكن التوصية بنظرية الفئة للعلاج البديل لأنواع أخرى من الإدمان. ومع ذلك ، لا تتعاطى ذاتياً ، في مدينتك ، على الأرجح ، يوجد متخصصون متاحون.

علم الجبر

بصراحة ، لم أكن أظن أنني منذ أكثر من أربعين عامًا كنت أتحدث بنثر.
جان باتيست موليير - تاجر في النبلاء

يجب أن يكون اسم الانضباط مألوفًا لك من المدرسة. في الواقع ، يعمل الجبر مع الهياكل الجبرية ، وفي المدرسة فقط الأعداد الصحيحة والأعداد المنطقية تمر من الهياكل ، وكذلك (في شكل مقتطع بقوة) هياكل حقيقية. والخبر السار هو أنه ليس عليك الآن حل المعادلات الجبرية التي عذبتك في المدرسة. إذا ظهر أي شيء في طريقك ، فسيتم تحديد ذلك بالفعل. إذا كان أي شيء ، فإن الكمبيوتر سوف يحسب لك ، إنه حديد. عليك أن تعرف بعض الهياكل الجبرية المحددة.

بادئ ذي بدء ، من المهم أن نفهم بوضوح مفهوم هيكل جبري . قراءة التعريف ، والحصول على فهم جيد. مراجعة تعريف المجموعة . في التحميل إلى ذلك ، توجد تعريفات لجميع المجموعات الفرعية ، مثل المونويدات والمجموعات شبه المجمعة والمجموعات الجماعية. اقرأها أيضًا ، لكن لا تهتم بالتذكر. تحتاج فقط المجموعات. بعد ذلك ، ادرس تعريف الخاتم والحقل .

تحذير! تجنب الأماكن التي يتم فيها ذكر الهياكل التي تحتوي على ناقل لانهائي. ما زلنا بحاجة إلى بعض هذه الأشياء التي لا نهاية لها ، لكنك على دراية بها. وهي: حلقة من الأعداد الصحيحة $$$\ mathbb {Z}$ مجال الأعداد المنطقية $$$\ mathbb {Q}$ وحقل الأعداد الحقيقية $$$\ mathbb {R}$ . العب معهم ، وتذكر قواعد المدرسة مثل "المبلغ لا يتغير من تغيير شروط البنود" وتبرير حقيقة أن هذه الهياكل هي حقا حلقات / حقول. اشرح لماذا لا تشكل الأعداد الصحيحة حقلاً.

نظرًا لأن الهدف النهائي لهذا الدليل هو تشفير بيضاوي بالتحديد ، فسيتعين عليك أن تتعرف على مفهوم كثير الحدود على الحقل . من أجل عدم دراسة التعاريف العامة ، اتصل بأخصائي حتى يخبر فقط ما هو وثيق الصلة بالغرض من رحلتك.

إذا كنت تحب الهندسة أكثر من الجبر ، يمكنك إلقاء نظرة على المنحنيات الإهليلجية أعلى الحقل $$$\ mathbb {R}$ . لكن ضع في اعتبارك أنه على الرغم من الاسم ، فإن هذه الكائنات المرئية بعيدة تمامًا عن مسارك.

من أجل الاهتمام ، يمكنك أيضًا التأمل في تعريفات الهياكل الجبرية الأخرى: الجبر (نعم ، الجبر مثل هذه البنية الجبرية ؛ لا تنزعج ، فهذه ليست تكرارا ، ولكن ليست متجانسة فقط) ، فضاء متجه (خطي) ...

العودة إلى الطريق. أنت تنتظر الحقل النهائي . قراءة مقال عنها. في الواقع ، ليس كل شيء مطلوب. هذه حالة أخرى عندما ، لتوفير الجهد ، من الأفضل أن تطلب على الفور المشورة من أخصائي. أدرك تصنيف الحقول المحدودة ، إنه بسيط. بالمناسبة ، سيكون من المثير للاهتمام معرفة سبب تسمية الحقول المحدودة أيضًا بحقول جالوا. تذكر ما فعلته في 20 عامًا وكن خجلًا.

إذا كنت تحب التصيد ، وتقدر قدراتك ، فحاول التعرف على بوريبيسي ومعادي البورباسي في المنتدى المواضيعي وحفرهم معًا.

نظرية المعلومات

إذا كنت قد ولدت بعد عام 1970 ، فمن المرجح أن يتم إخبارك في المدرسة الثانوية عن البتات والبايت. ليست هناك حاجة خاصة إلى وحدات البايت في العلوم الأساسية ، لكن مفهوم الشيء يحتاج إلى معرفة بوضوح. ألقِ نظرة على الكتاب المدرسي إذا لزم الأمر.

عد أو اكتشف في الكتاب المدرسي عدد متواليات البتات الإجمالية بطول معين. العب مع الأبجدية عن طريق ترميز الحروف في سلسلة من البتات. فكر أو اقرأ في الكتاب المدرسي كيفية رمز الأعداد الصحيحة. النظر في ما هو مفيد في نظرية المعلومات هو لوغاريتم القاعدة الثانية.

نظرية الاحتمالات

أي شخص لديه ضعف في الطرق الحسابية للحصول على أرقام عشوائية هو خاطئ دون أدنى شك.
جون فون نيومان

يعد سوء فهم نظرية الاحتمالات وتطبيقها على القضايا العملية أهم مصدر للخطأ البشري. هذا موضوع مهم للغاية ، حاول تخصيص بعض الوقت للتعرف على أساسياته. ليس بالضرورة الآن ، لأنه من أجل الهدف النهائي لطريقنا ، لا يكفي سوى قسم واحد من الأقسام الفرعية المطبقة - توليد الأرقام العشوائية.

الآن يكفي أن تدرك أن مسألة إنشاء أرقام عشوائية معقدة للغاية ، حيث أن المعاهد بأكملها تتعامل معها منذ عقود. حتى تحديد ما هي فرصة معقدة للغاية. لا يمكنك فقط أخذ رقم عشوائي. لسوء الحظ ، هناك فخ لغة يجعل من الصعب فهم الموضوع. إن كلمة عشوائي ، وكذلك ما يعادلها بالروسية ، "عشوائي" ، على الرغم من أنها تعني بدرجة أقل ، كلمة "فظيعة" ، بينما بالنسبة للعديد من التطبيقات ، وخاصة بالنسبة للتشفير ، تحتاج إلى الاختيار بعيدًا عن العشوائية.

إذا بدا لك أنك تفهم نظرية الاحتمال جيدًا ، فاستشر أخصائيًا. إذا سمح الوقت بذلك ، اذهب بعيدًا لتفسير التفسير متعدد الميكانيكا (Everett) للميكانيكا الكمومية. لا تبتعد ، أنت تنتظر في المنزل.

نظرية الحوسبة

هل من الممكن أن تجعل هذا المترجم يحذر دائمًا من أن البرنامج يمكن أن يستمر في دورات؟

لن تحتاج هذا القسم في الوقت الحالي. من المفيد أن ندرك أنه ليس لأي وظيفة محددة رياضيا ، فهناك خوارزمية تحسبها. إذا كنت تشعر بالقوة في نفسك ، خذ رحلة عبر تاريخ القضية ، فحاول فهم التعاريف والنتائج الأساسية. لا إرهاق ، هذا الموضوع اختياري.

فقط لتقليل إجهادك من إدراك جهلك الخاص ، سوف أبلغكم أن السؤال الذي طرح في الصورة قد طرح عليّ من قبل أستاذ محترم في الفيزياء والرياضيات ، والذي يقع مجال اهتماماته على مسافة بعيدة عن علم الكمبيوتر. إذا فهمت الموقف القصصي ، فإن رحلتك كانت مفيدة. شجع نفسك.

نظرية التعقيد

لسوء الحظ ، تطورت العلوم الكلاسيكية بحيث تستند نظرية التعقيد ، بالمعنى الدقيق للكلمة ، إلى نظرية الحدود من التحليل الرياضي. هذا كله لأن علماء الرياضيات الأنانيين لم يهتموا بك. اقتربوا من التعقيد ، واقفين بالفعل على أكتاف العمالقة ، واستخدموا الأدوات التي يمتلكونها بأنفسهم في الكمال. من أجل أهدافنا المتواضعة ، كان من الممكن بناء نظريتنا الصغيرة المنفصلة حول التعقيد ، والتي يود حتى المتناهية الصغر. لكن ، على سبيل المثال ، ليس لدي القوة ولا الدافع لإنهاء بناء جزء من المشهد الطبيعي. لذلك ، لا يزال يتعين عليك اللجوء إلى ما يسمى كلمة ماتان.

التحليل الرياضي

أنا لست بوتان ، أنا فقط أحب ماتان.

اقرأ تعريف حد التسلسل (لا تحتاج إلى حد وظيفة). يستبدل علماء الرياضيات جميع التعبيرات مثل "مساحة كهذه" بعبارة "مجموعة من الأرقام الحقيقية" ، ويفضل علماء الرياضيات التعميم ، لكنك لا تحتاج إليها. تأكد من أنه يمكنك تحليل التعبيرات التي تحتوي على كلمة $$$\ lim$ . على الأرجح ، سيكون لديك صعوبات ، وهذا أمر طبيعي. صدقوني ، مفهوم الحد هو بديهي للغاية ، تحتاج فقط إلى تحفيز الجزء المقابل من الحدس الخاص بك. اطلب من أخصائي أن يعلق على نص التعريف. ارسم الرسومات ، العب مع تسلسل بسيط. إذا سمح الوقت ، اذهب في رحلة لإلقاء نظرة على الحد الثاني الرائع.

حتى لو لم يكن لديك فهم كامل للحد المسموح به ، يمكنك المتابعة على الفور إلى O-notation. تحتاج فقط إلى "O" الكبيرة ، ولكن الحمل يذهب "O" الصغيرة وجميع أنواع ثيتا وأوميغا. لا إرهاق ، لبداية تحتاج فقط إلى فهم ما هي عليه تقريبا $$$O (1) ، O (N) ، O (\ log N)$ . اكتشف ذلك ، ولكن حاول أن تتخيل ذلك بنفسك $$$O (\ log N)$ مجرد لوغاريتم ، وليس لوغاريتم لسبب ما. ثم ارح قليلاً واحبس يديك $$$O (N ^ 2)$ و $$$O (2 ^ N)$ . انظر الي $$$O (N ^ k)$ (تذكر السياق: هنا N متغير ، k هي معلمة). التفكير في سبب الحديث عن النمو متعدد الحدود متى $$$N ^ k$ - مجرد حالة أحادية ، أي حالة خاصة كثيرة الحدود ، لكنها لا تضع الكثير من الحدود متعددة الحدود الكاملة تحت "O". (حتى إذا كنت لا تتحدث اللاتينية ، فمن المحتمل أنك خمنت بالفعل أن كثير الحدود هو نفسه متعدد الحدود ، والمونومى هو الأحادي.) تلميح: السبب مشابه جدًا للسبب الذي "ببساطة لوغاريتم" وليس "اللوغاريتم" على الأرض ". اتصل بأخصائي لتوضيح هذه المشكلات. تعلم مقارنة هذه "O" مع بعضها البعض.

ملاحظة: o- الترميز مثال نادر عندما لا يكون الترميز الرياضي ثابتًا. في السجل $$$f (N) = O (N)$ يتم استخدام علامة المساواة ، في حين أنها تنطوي على شيء آخر ، وهي: "وظيفة $$$f (N)$ ينتمي إلى الصف $$$O (N)$ ". أي أنه يجب استخدام علامة غير متماثلة $$$\ في$ ولكن هذا هو التقليد. حسنًا ، الآن ترى أن علماء الرياضيات ليسوا بلا خطيئة. ربما سيصبح الأمر أسهل بالنسبة لك من إدراك هذه الحقيقة.

نظرية التعقيد الحسابي - تابع

لوغاريتم - وظيفة ، من حيث المبدأ ، محدودة.

بعد قليل من إدراج matan ، يمكنك بسهولة السيطرة على مقياس لقياس التعقيد مقارب. عادةً ما يتم قياس مدى تعقيد الخوارزميات من حيث وقت تنفيذها: في بعض الأحيان يتحدثون عن الوقت المعتاد المقاس باستخدام الساعة (جيدًا ، متى يتم تحميل علامة تبويب المتصفح هذه؟) ، أحيانًا حول عدد دورات المعالج أو خطوات الكمبيوتر المجرد. أولئك الذين يميلون أكثر نحو الفيزياء يفضلون قياس التعقيد في وحدات الطاقة ، على سبيل المثال ، في كمية وقود الديزل المستهلكة لآلة تورينج. كل طرق القياس هذه متساوية تقريبًا. من المهم معرفة كيف يعتمد الوقت المستغرق (أو الطاقة) على حجم بيانات الإدخال الخاصة بالخوارزمية. هذا N تحت "O" كبير في التقدير المقارب وهو حجم بيانات الإدخال ، معبراً عنه بالبتات. وافق الأخصائيون على التفكير في أنه إذا كان تعقيد الخوارزمية لا ينمو بوتيرة متعددة الحدود ، فهو "سهل" أو "صعب". من المناسب العودة قليلاً وتذكر كيفية مقارنة الوظائف مع بعضها البعض من حيث البرودة ، أي من حيث سرعة النمو غير المقارب.

إذا لاحظت أن العبارة التي تم الإدلاء بها في الرسم البياني خاطئة ، شجع نفسك. تم تسليمه من قبل مدرس جامعي في الأساليب الحسابية. معرفة هذا السياق ، والتفكير على وجه التحديد ما كان يدور في خلد.

وظائف في اتجاه واحد. اقرأ التعريف. . , , , .

, , . , . , . ?

«». « », — « ». <…> . <...> . , , .
—

, . ! , , (, , ). , . - . , . ? . , ?

شكر

, . Shapelez .