التبرير الرياضي لعدم ملاءمة الجري في السلم الكهربائي في المترو

خلافا لقواعد استخدام المترو ، من أجل توفير الوقت ، ركض كل واحد منا مرة واحدة على الأقل في حياتنا أسفل السلم الكهربائي. للوهلة الأولى ، يبدو أن هذا منطقي وصحيح تمامًا: إذا كنت ترغب في المغادرة بشكل أسرع - حاول أن تكون على المنصة في أقرب وقت ممكن. ومع ذلك ، على الفور تقريبًا ، يتبادر إلى الذهن السيناريو التالي: أنت تتجه إلى أسفل المصعد ، وتنزل إلى المنصة ، وتغلق أبواب السيارة أمام أنفك مباشرة. أثناء انتظارك القطار التالي - الأشخاص الذين استيقظوا على السلالم المتحركة في نفس الوقت الذي يتوفر لديك فيه الوقت للوقوف صامدين في هدوء ويستقلون القطار التالي. في هذه الحالة ، لا يوجد مكسب. إذن ما مدى عقل المصعد وهل يستحق القيام به على الإطلاق؟ أسارع لإرضائك - تم العثور على الجواب! في ما يلي تبريرات رياضية لعدم ممانعة (نعم ، إنها ليست كذلك) للركض في السلم الكهربائي في المترو.

بيان المهمة

قبل الانتقال إلى التفكير الرياضي ، تجدر الإشارة إلى أنه ، بطبيعة الحال ، لست أول من يفكر في هذه المسألة على الإطلاق. على الإنترنت ، يمكنك العثور على عدد كاف من المقالات وحتى الأخبار من القنوات الفيدرالية حول هذا الموضوع. ومع ذلك ، في كل مرة يكمن جوهر مثل هذه التجارب في الجري المعتاد لأسفل المصعد مع المقارنة اللاحقة للوقت المكتسب مع وقت الشخص الذي يقف على المصعد. أفضل قليلاً إذا كان المؤلفون يحاولون تقييم فعالية الإنحدار. حتى أفضل إذا كانت لا تزال توفر الإحصاءات. بالنسبة للإحصاءات ، بالمناسبة ، سأقول شكرًا خاصًا أقل قليلاً. فيما يتعلق بعدم وضوح هذه التجارب والافتقار إلى استنتاجات عملية ، فقد صممت ، ونفذت بعد ذلك ، تحليلًا للعملية المستمرة.

وهكذا ، نقوم بصياغة شروط المشكلة ونشير إلى القيود:

1. تشمل التجربة (الذهنية) شخصين يقتربان من السلالم المتحركة في نفس الوقت في لحظة عشوائية من الوقت وليس لديهما فكرة عن مكان القطار.
2. يقف أحد هؤلاء الأشخاص على سلم متحرك ويقضي وقتًا في الهبوط. $$ يساوي وقت حركة المصعد.
3. والثاني يسرع المصعد ، وزيادة سرعته في $$ مرات ، وبالتالي تقليل وقت الهبوط بنفس عدد المرات: $$ .
4. يُعتبر الفاعل فعالًا مثل هذا الهبوط المتسارع ، مما أدى إلى حقيقة أن الشخص الذي يقف على السلالم المتحركة ليس لديه وقت الصعود إلى القطار ، حيث يكون لدى الشخص الذي يركض على السلم الكهربائي وقت الصعود.
5. دلالة بواسطة $$ - احتمال الهبوط الفعلي. بعد ذلك ، وفقًا لتوازن ناش ، يكون الشخص مستعدًا لاغتنام الفرصة والسقوط إلى السلالم المتحركة فقط إذا كانت احتمالية الهبوط الفعلي أكبر من أو تساوي احتمال حدوث نزول غير فعال أو توقف في المكان ، أي 0.5. إذا كان احتمال الهبوط الفعلي أكبر من أو يساوي 0.5 ، فسيتم استدعاء قرار الجري في السلم المتحرك المناسب . إذا كان أقل من 0.5 - غير عملي .
6. نحن نتجاهل حقيقة أنه في الحياة الواقعية ، كقاعدة عامة ، من الضروري قطع مسافة أبعد من السيارة بعد مغادرة المصعد أو الانتظار حتى يترك الناس السيارة ، تمر القطارات بفواصل زمنية متغيرة وتقف بلا حراك لفترة من الوقت قبل فتحها وبعد إغلاق الأبواب ، أي أننا سنفترض أنه إذا كان القطار واقفًا في المحطة وقت مغادرة المصعد ، فتفتح أبوابه وينتهي مشارك التجربة على الفور في السيارة ، ويفتح القطار نفسه (يغلق) الأبواب ويصل (يغادر) إلى المحطة (من المحطة) على الفور و dnomomentno.

تقدم القرار

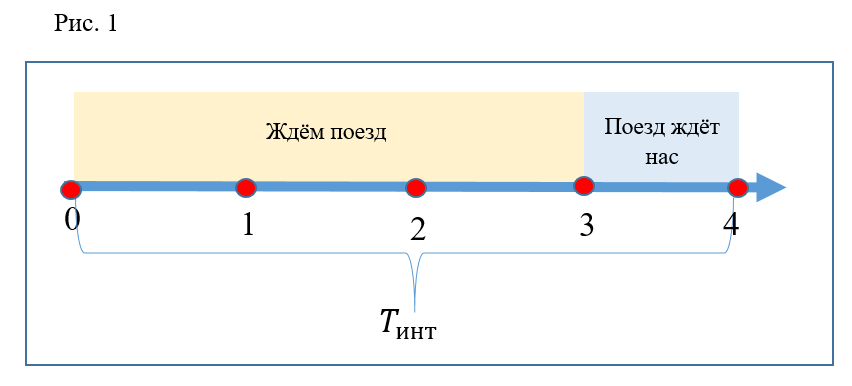
دعنا نرسم محور الوقت (الشكل 1). سيكون المحور بأكمله فترات زمنية متتالية بين القطارات. فيما يلي ، سيتم النظر في فاصل واحد فقط. قسّم الفاصل الزمني الموضح إلى 4 شرائح متساوية. النقطة 0 على هذا المحور تتوافق مع اللحظة التي يغادر فيها القطار المحطة. النقطة 3 تتوافق مع وصول القطار وفتح الأبواب. النقطة 4 - إغلاق الأبواب ومغادرة القطار. وبالتالي ، لراحة التمثيل البياني والحسابات ، يتم حساب الفاصل الزمني بين القطارات بين لحظات رحيل القطارات من المحطة. أول ثلاثة أجزاء هي الوقت الذي يُجبر فيه المسافرون على انتظار القطار القادم. الجزء الرابع هو وقت توقف القطار ، حيث يمكن للركاب الصعود إليه. ضع ذلك الوقت أيضًا $$ (وقت الهبوط على السلالم المتحركة) يساوي قسمين. عامل $$ يساوي 2 ، وهذا هو ، وقت النزول تشغيل 2 مرات أقل ويساوي قطعة واحدة.



الآن ، لتحديد الاحتمال $$ ، معرفة في أي فترة من الوقت سوف يؤدي قرار الركض إلى حقيقة أن النزول سيكون فعالا. على سبيل المثال ، إذا اقترب المشاركون من المصعد في الوقت 0 ، فسيكون الأول على المنصة في الوقت المناسب $$ (الشكل 2) ، والثاني في وقت سابق ، في الوقت الراهن $$ . ولكن ، كما يتضح من الشكل ، لا يوجد قطار في المحطة في أي من هذه اللحظات ، مما يعني أن الجري كان غير فعال.



فكر في حالة أخرى (الشكل 3): يقترب المشاركون في التجربة من السلالم المتحركة في الوقت 2. كما في الحالة السابقة ، ستكون الأولى في المنصة في الوقت المناسب $$ ، والثاني في وقت سابق ، في الوقت الراهن $$ . لكن من الواضح أنه في كلتا الحالتين يكون القطار في المحطة. لذلك ، سيكون لدى كليهما وقت الصعود إلى القطار نفسه ، لذلك ، كان الجري غير فعال.



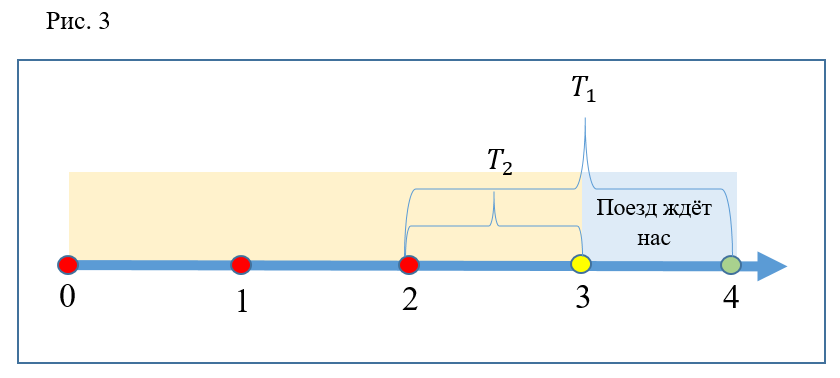
علاوة على ذلك ، من السهل أن نفهم أنه في أي وقت في الفترة الفاصلة من 2 إلى 3 ، يكون الجري هبوطًا فعالًا ، نظرًا لأن الشخص الهارب قادر دائمًا على ركوب القطار ، وليس القطار الهارب. إذا اخترت نقاط زمنية بين 3 و 4 ، فحينها يتأخر كل من المشاركين في القطار ويضطرون إلى الانتظار للحصول على القطار التالي معًا ، وهذا يعني أن الجري مرة أخرى غير فعال.

اتضح أنه من بين 4 فترات زمنية تقليدية ، يكون الجري فعالًا فقط إذا اقترب المشاركون من السلالم المتحركة من 2 إلى 3 مرات (الشكل 4). احتمال الدخول فيه هو 1/4. لذلك ، وفقًا لشروط المهمة المحددة ، فإن اتخاذ قرار الجري أمر غير عملي ، لأن المشارك الثاني من المرجح (مع احتمال 3/4) أن يذهب هباء وسيضطر إلى الانتظار حتى القطار مع الأول ، والذي جاء لاحقًا.



ستكون الملاحظات التالية عادلة تمامًا:

1. الفواصل الزمنية بين القطارات يمكن أن تقل وتزيد. قد يزيد وقت الانتظار ، وقد يقل وقت الانتظار (مع نفس الفترة الزمنية) والعكس بالعكس.
2. تكون سرعة المصعد لأسفل ثابتة ، لكن يمكن أن يتغير وقت الهبوط ، حيث قد تكون المحطات أكثر عمقًا أو أقل.
3. قد لا يعمل المشارك الثاني جيدًا 2 ، ولكن 3 أو حتى 4 مرات أسرع من المصعد.

لتقييم تأثير التغييرات في العوامل المذكورة أعلاه ، من الضروري استخلاص العلاقة بين هذه القيم واحتمال الحصول على السلم الكهربائي في وقت يكون فيه الجري فعالًا.

للقيام بذلك ، سوف نقوم بتصوير حالة أخرى (الشكل 5). نترك جميع البيانات الأصلية دون تغيير باستثناء واحد: معامل $$ زيادة إلى 4. وهذا هو ، سيكون المشارك الثاني في أسفل 4 مرات أسرع من الأول. لتوفير الراحة للصورة ، نقسم الفاصل الزمني لدينا إلى 8 أجزاء متساوية. وبالتالي ، فإن وقت الهبوط على المصعد يساوي الآن 4 أجزاء ، ويتوقف القطار عند قسمين ، ووقت الانتظار هو 6 ، ووقت الهبوط لتشغيل وحده. ليس من الصعب معرفة أن الآن طول الفاصل الزمني "الفعال" (من 4 إلى 7 نقاط في الوقت المناسب) هو 3. وهذا هو الاحتمال $$ يساوي 3/8. هذا بالفعل أكثر مما كان عليه الحال في الحالة الأولى ، لكننا لم ننفذ هذه التغييرات على الإطلاق لتقييم الاحتمال.



استنادا إلى الشكل 4 والشكل 5 ، فمن الواضح أن طول الجزء "الفعال" هو $$ . اقسمه على طول الفاصل الزمني واحصل على الاحتمال $$ حيث $$ .
نقوم بإجراء سلسلة من التحولات: $$$$ .
الصيغة النهائية: $$ .

بناءً على هذه الصيغة ، يمكن استخلاص العديد من الاستنتاجات الأساسية مرة واحدة:

1. لا تتأثر قيمة الاحتمال بالتغيرات في وقت الانتظار وتدريب وقت الانتظار إذا لم يتغير الفاصل الزمني الإجمالي (الشكل 6).
   
   
   
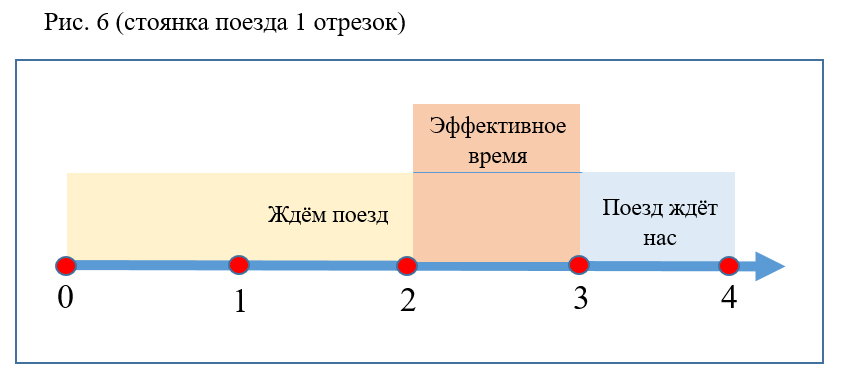
2. كلما زادت الفترة الفاصلة بين القطارات ، انخفض الاحتمال P (الشكل 7).
   
   
   
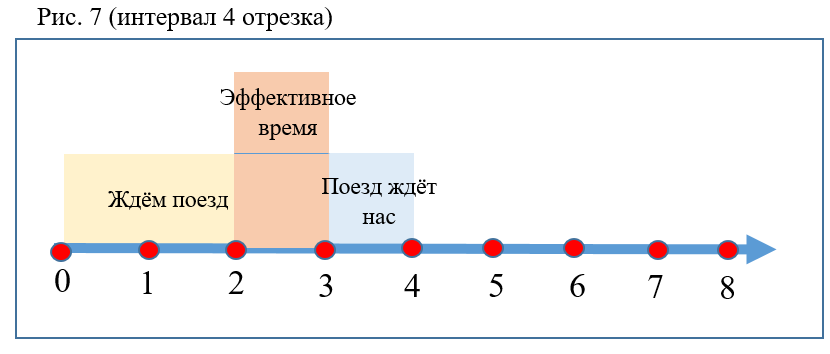
3. يزيد الاحتمال إذا زادت نسبة وقت الهبوط على المصعد إلى الفاصل و / أو زاد معامل K.
   

الاختيار الإخلاص

الآن دعونا نرى مدى صحة الصيغة المشتقة؟

للتحقق من صحة الصيغة ، ننتقل إلى الإحصائيات ، التي كانت مفيدة للغاية في عام 2014 من قبل مراسل القرية. أعرب عن تقديري ، وبطبيعة الحال ، في نهاية المقال سأترك رابطًا للمقال الأصلي. من الجيد أيضًا أن يتم تقديم الإحصاءات كرسومات بيانية بصرية.

تجربة 1. محطة مترو Chekhovskaya



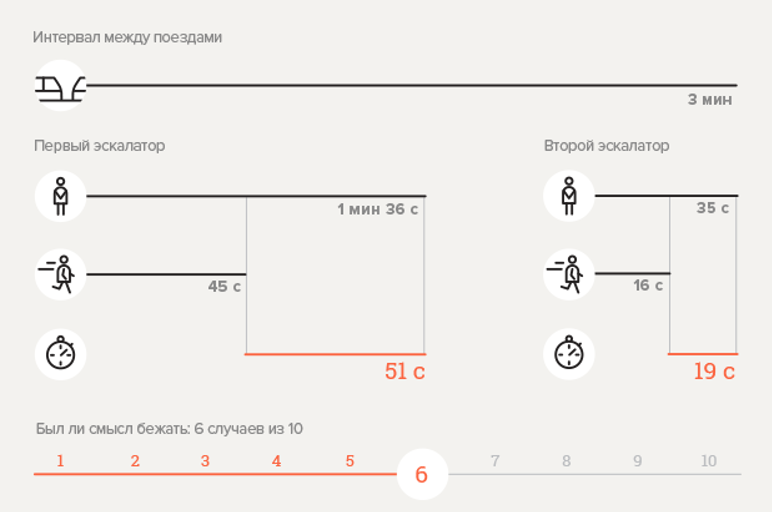
احسب الاحتمال $$ .
هنا $$ . $$ . $$ . $$ . $$ .

النتيجة التي تم الحصول عليها ، على ما يبدو ، تختلف عن البيانات التجريبية. هل الصيغة خاطئة؟ لا! يمكن أن نرى من الرسم التوضيحي أن النزول إلى المحطة يتضمن رحلة على سلالم متحركة ، ومع ذلك ، فإن وقت الانتقال بينهما لا يؤخذ في الاعتبار. إذا افترضنا ، من أجل الموثوقية ، أن الانتقال يستغرق 30 ثانية على الأقل ، فعندئذ نستبدل قيمة جديدة $$ حصلنا على: $$ . $$ ، وهو أقرب بكثير إلى النتيجة التجريبية. تجدر الإشارة أيضًا إلى أن التجربة قدمت 10 مرات فقط. من خلال زيادة عدد التكرارات ، من الممكن تحقيق تزامن شبه كامل للبيانات المحسوبة مع النتائج التي تم الحصول عليها أثناء التجربة.

التجربة 2. محطة المترو "فيكتوري بارك"



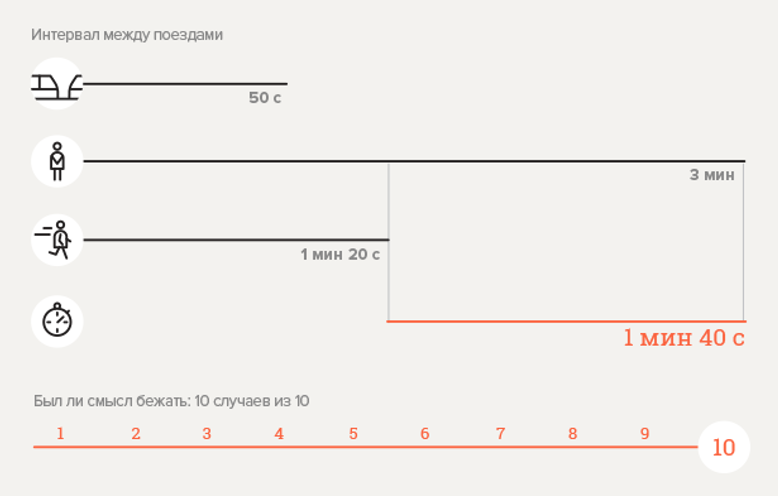
احسب الاحتمال $$ .
هنا $$ . $$ . $$ . $$ . $$ .
يمكن أن نرى أن لدينا احتمال أكبر من واحد. ولكن لا يوجد تناقض هنا. إذا نظرت إلى الشكل العام للمعادلة ، يصبح من الواضح أنه في حالة ما إذا كان وقت الهبوط على المصعد يساوي الفاصل الزمني بين القطارات ، فإن الزيادة في السرعة بمقدار 2 مرات على الأقل ستجعل من المحتمل أن يكون تسارع الهبوط الفعال يساوي 0.5. إذا كان وقت سفر المصعد أكبر من الفاصل الزمني ، فعندئذٍ بنفس المعامل $$ احتمال اصطياد قطار في وقت سابق سوف يزيد فقط. أخيرًا ، إذا كان وقت الهبوط على السلالم هو الفاصل الزمني مرتين أو أكثر ، فسيكون الشخص الذي يركض في 100٪ من الحالات في الوقت المناسب للقطار الذي لن يكون للباقي على المصعد وقت. هذا هو التأثير الذي نلاحظه في هذه التجربة: خلص المراسل إلى أنه غسل ​​في 10 من أصل 10 حالات.

تجربة 3. محطة مترو بارك كولتوري



احسب الاحتمال $$ .
هنا $$ . $$ . $$ . $$ . $$ .

مرة أخرى خطأ؟ لا على الإطلاق. يمكن أن نرى أنه ، كما هو مذكور أعلاه ، فإن وقت الهبوط على السلالم المتحركة هو مرتين الفاصل الزمني بين القطارات. وقت التشغيل أقل مرتين. اتضح أن كل نزول يجب أن يكون فعالا. لكن لا تنسَ أنه قبل بدء المناقشة ، توصلنا إلى الافتراض فيما يتعلق بالإغلاق الفوري للأبواب والمغادرة الفورية للقطار من المحطة. إذا كنت تتخيل مثل هذا الخيار كما هو موضح في الشكل 8 ، يصبح من الواضح أنه في الحياة الواقعية قد لا يكون لدى الشخص الهارب الوقت للجلوس عند النقطة 1 (على سبيل المثال ، سوف يغادر القطار قبل ذلك بقليل) وعند النقطة 2 ، سيتأخر القطار قليلاً ، وبعد ذلك سوف يجلس فيه شخص لا يعمل مع شخص متأخّر يعمل على القطار السابق.



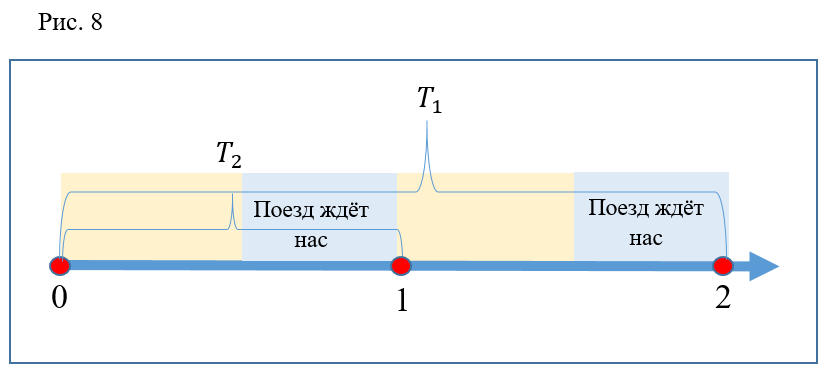
أفترض أنه في كلتا الأوقات "غير الفعالة" حدث ذلك. هناك كل الأسباب التي تدعو إلى القول إنه مع زيادة عدد مرات تكرار التجربة ، تميل النسبة المئوية للتشغيل "الفعال" إلى 100٪.

النتائج

الآن ، بناءً على البيانات التجريبية المتاحة ، كان من الممكن تأكيد صحة الصيغة ، وسوف نقوم بتحليلها واستخلاص النتائج. منذ البداية ، اتفقنا على أننا سننظر في قرار الركض السريع إذا كان احتمال الهبوط الفعلي أكبر من أو يساوي 0.5. هذا يعني حرفيًا ، إذا استطعنا التأكد من أننا في نصف الحالات على الأقل سنواجهها لسبب وجيه ، فإن الأمر يستحق المخاطرة والتشغيل ، لأنه إذا تأخرنا ، فلن نفقد شيئًا من الناحية العملية. بناءً على ما تقدم ، نعيد كتابة صيغة الاحتمال كما يلي: $$ .

من المثير للاهتمام أنه ، كما اكتشفنا بالفعل ، من المنطقي أن نركض دائمًا متى $$ . في الوقت نفسه ، صحيح أيضا أنه إذا $$ ، بغض النظر عن السرعة التي تجري بها ، فإن احتمال ركوب القطار في وقت مبكر أقل من 0.5 ، لأنه من الواضح ذلك $$ لن تكون أكبر من أو تساوي 1.

الآن دعونا نلقي نظرة على سرعة المراسل. في المتوسط ​​، تبلغ سرعة المصعد نحو ضعفي (وقت الهبوط أقل مرتين). بشكل عام ، تتزامن هذه البيانات مع نتائج تجاربي الخاصة (لا أرى نقطة إحضارها). كقاعدة عامة ، من الصعب بالفعل تطوير سرعة ، فإن معامل K الذي سيكون له 3 على الأقل: على السلالم المتحركة الحقيقية هناك الكثير ممن يرغبون في الجري ، علاوة على ذلك ، الأشخاص الذين يقفون على يسارهم أو قد تتداخل أشياءهم (الحقائب ، حقائب السفر). وبالتالي، $$ و $$ . وهذا هو ، فإن قرار الإسراع لن يكون مناسبا إلا إذا كانت النسبة $$ لا تقل عن 1. وهذا ممكن فقط عندما يكون وقت الهبوط على السلالم المتحركة أقل من الفاصل الزمني بين القطارات. في المترو الحقيقي ، حيث يبلغ متوسط ​​الفاصل بين القطارات دقيقتين ، لا يمكن لجميع المحطات أن تفتخر بانحدار طويل. كقاعدة عامة ، حتى في مترو سان بطرسبرغ ، يستغرق وقت السفر في المصعد حوالي دقيقة واحدة و 30 ثانية ، أي أقل بمقدار 0.75 مرة من الفاصل الزمني. من هذا يتبع الاستنتاج الأساسي الواضح والأكثر أهمية: إذا كنت على يقين من أن المصعد في هذه المحطة يتحرك أقل من الفاصل الزمني بين القطارات ، فعندئذٍ ليس من العملي الركض على طوله.

ملاحظة: يرجى مراعاة حقيقة أن هذه المهمة لا تأخذ في الاعتبار الحاجة إلى الدخول في عربة محددة. يتعلق الأمر حصريًا بالوصول إلى المنصة ثم ركوب القطار.

مصدر البيانات التجريبية: القرية . شكرا مرة اخرى!