تم إعداد ترجمة المقال خاصة للطلاب في الدورات الأساسية والمتقدمة "الرياضيات لعلوم البيانات".
نظرية بايز هي واحدة من النظريات الأكثر شهرة في الإحصاءات ونظرية الاحتمالات. حتى إذا كنت لا تعمل مع حساب المؤشرات الكمية ، فمن المحتمل أن تكون على دراية بهذه النظرية في مرحلة ما استعدادًا للامتحان.
P (A | B) = P (B | A) * P (A) / P (B)هذا ما يبدو ، لكن ماذا يعني وكيف يعمل؟ اليوم سنكتشف ونذهب إلى عمق نظرية بايز.
أسباب لتأكيد حكمنا
ما هو الهدف الكامل من نظرية الاحتمالات والإحصاءات؟ واحد من أهم الاستخدامات يتعلق باتخاذ القرارات في ظل عدم اليقين. عندما تقرر إجراء أي إجراء (ما لم تكن بالطبع شخصًا معقولًا) ، فإنك تراهن أنه بعد الانتهاء من هذا الإجراء ، ستترتب عليه نتيجة أفضل مما لو لم يحدث هذا الإجراء ... لكن المراهنة شيء لا يمكن الاعتماد عليها ، كيف يمكنك أن تقرر في النهاية ما إذا كنت ستتخذ هذه الخطوة أم لا أم لا؟
بطريقة أو بأخرى ، تقوم بتقييم احتمال حدوث نتيجة ناجحة ، وإذا كان هذا الاحتمال أعلى من قيمة عتبة معينة ، فأنت تأخذ خطوة.
وبالتالي ، فإن القدرة على تقييم احتمال النجاح بدقة أمر بالغ الأهمية لاتخاذ القرارات الصحيحة. على الرغم من حقيقة أن العشوائية ستلعب دائمًا دورًا في النتيجة النهائية ، يجب أن تتعلم استخدام هذه العشوائية بشكل صحيح وتحويلها إلى مصلحتك بمرور الوقت.
وهنا تدخل نظرية بايز حيز التنفيذ - إنها توفر لنا أساسًا كميًا للحفاظ على إيماننا بنتيجة الإجراء مع تغير العوامل البيئية ، والتي بدورها تتيح لنا تحسين عملية صنع القرار بمرور الوقت.
دعنا نحلل الصيغة
دعنا ننظر إلى الصيغة مرة أخرى:
P (A | B) = P (B | A) * P (A) / P (B)هنا:
- P (A | B) - احتمال حدوث الحدث A ، شريطة أن يكون الحدث B قد حدث بالفعل ؛
- P (B | A) - احتمال حدوث الحدث B ، شريطة أن يكون الحدث A قد حدث بالفعل. يبدو الآن وكأنه نوع من الحلقة المفرغة ، لكننا سنفهم قريبًا لماذا تعمل الصيغة ؛
- P (A) - احتمال مسبق (غير مشروط) لحدوث الحدث A ؛
- P (B) - احتمال مسبق (غير مشروط) لحدوث الحدث B.
P (A | B) مثال لاحتمال خلفي (مشروط) ، أي يقيس احتمال حالة معينة من العالم المحيط (أي الحالة التي حدث فيها B). في حين أن P (A) مثال على الاحتمال المسبق ، والذي يمكن قياسه في أي حالة من العالم المحيط.
دعونا ننظر في نظرية بايز في العمل على سبيل المثال. لنفترض أنك أكملت مؤخرًا دورة تحليل بيانات من bootcamp. لم تتلق ردًا من بعض الشركات التي أجريت معها مقابلة ، وتبدأ في القلق. لذا ، فأنت تريد حساب احتمال أن تقدم لك شركة معينة عرض عمل ، شريطة أن تمر ثلاثة أيام ولم يتصلوا بك.
نعيد كتابة الصيغة من حيث مثالنا. في هذه الحالة ، تكون النتيجة A (
العرض ) هي استلام عرض العمل ، والنتيجة B (
NoCall ) هي "عدم وجود مكالمة هاتفية لمدة ثلاثة أيام". بناءً على ذلك ، يمكن إعادة صياغة صيغتنا على النحو التالي:
P ( العرض | NoCall ) = P ( NoCall | العرض ) * P ( العرض ) / P ( NoCall )قيمة
P ( Offer | NoCall ) هي احتمال تلقي عرض ، بشرط عدم وجود اتصال في غضون ثلاثة أيام. هذا الاحتمال صعب للغاية للتقييم.
ومع ذلك ، فإن الاحتمال معكوس ،
P ( NoCall | عرض ) ، أي عدم وجود مكالمة هاتفية لمدة ثلاثة أيام ، بالنظر إلى أنه في النهاية تلقيت عرض عمل من الشركة ، فمن الممكن تماما أن نعلق بعض القيمة. من خلال المحادثات مع الأصدقاء ومقدمي التوظيف والمستشارين ، ستجد أن هذا الاحتمال ضئيل ، ولكن في بعض الأحيان قد تظل الشركة صامتة لمدة ثلاثة أيام إذا كانت لا تزال تخطط لدعوتك للعمل. لذلك تقييمك:
P ( NoCall | العرض ) = 40 ٪40 ٪ ليس سيئا ويبدو أنه لا يزال هناك أمل! لكننا لم ننته بعد. الآن نحن بحاجة إلى تقييم
P ( العرض ) ، واحتمال الذهاب إلى العمل. يعلم الجميع أن العثور على وظيفة هو عملية طويلة وصعبة ، وقد تضطر إلى الذهاب إلى مقابلة عدة مرات قبل أن تتلقى هذا العرض ، حتى تتمكن من تقييم:
P ( العرض ) = 20 ٪الآن علينا فقط تقييم
P ( NoCall ) ، احتمال عدم تلقي مكالمة من الشركة في غضون ثلاثة أيام. هناك العديد من الأسباب وراء عدم استدعائك في غضون ثلاثة أيام - فقد يرفضون ترشيحك أو ما زالوا يجرون مقابلات مع مرشحين آخرين ، أو يكون المجند مريضًا ببساطة ولا يتصل بذلك. حسنًا ، هناك العديد من الأسباب وراء عدم إجراء مكالمة ، لذلك تقوم بتقييم هذا الاحتمال على النحو التالي:
P ( NoCall ) = 90٪والآن ،
وبوضع كل ذلك معًا ، يمكننا حساب
P ( العرض | NoCall ) :
P ( العرض | NoCall ) = 40٪ * 20٪ / 90٪ = 8.9٪هذا صغير جدًا ، لذا ، لسوء الحظ ، من المنطقي ترك الأمل لهذه الشركة (والاستمرار في إرسال السير الذاتية للآخرين). إذا كان لا يزال يبدو قليلاً مجردة ، لا تقلق. شعرت بنفس الطريقة عندما علمت لأول مرة عن نظرية بايز. الآن دعونا نرى كيف وصلنا إلى هذه 8.9 ٪ (ضع في اعتبارك أن درجة 20 ٪ الأولية الخاصة بك كانت منخفضة بالفعل).
الحدس وراء الصيغة
تذكر ، قلنا أن نظرية بايزي توفر الأساس لتأكيد أحكامنا؟ إذن من أين أتوا؟ يتم أخذهم من الاحتمال المسبق
P (A) ، والذي يسمى في مثالنا
P ( العرض ) ، في الواقع ، هذا هو حكمنا المبدئي على مدى احتمال حصول الشخص على عرض عمل. في مثالنا ، يمكنك افتراض أن الاحتمال المسبق هو احتمال حصولك على عرض عمل في نفس اللحظة التي تغادر فيها المقابلة.
تظهر معلومات جديدة - مرت ثلاثة أيام ولم تقم الشركة بالاتصال بك مرة أخرى. وبالتالي ، فإننا نستخدم أجزاء أخرى من المعادلة لضبط احتمال مسبق لحدث جديد.
دعونا نلقي نظرة على الاحتمال
P (B | A) ، والذي يسمى في
مثالنا P ( NoCall | Offer ) . عندما ترى نظرية بايز لأول مرة ، تسأل نفسك: كيف تعرف من أين تحصل على الاحتمال
P (B | A) ؟ إذا لم أكن أعرف ما هو الاحتمال
P (A | B) ، فكيف يجب أن أعرف بطريقة سحرية ما هو الاحتمال
P (B | A) ؟ أذكر عبارة
تشارلز مونجر ذات مرة قال:
"الوجه ، دائما الوجه!"
- تشارلز مونجر
لقد كان يعني أنه عندما تحاول حل مشكلة صعبة ، فأنت بحاجة إلى قلبها رأسًا على عقب والنظر إليها من زاوية مختلفة. هذا هو بالضبط ما تفعله نظرية بايز. دعونا إعادة صياغة نظرية بايز من حيث الإحصاءات من أجل جعلها أكثر قابلية للفهم (تعلمت عن هذا
من هنا ):
بالنسبة لي ، على سبيل المثال ، يبدو هذا السجل أكثر وضوحًا. لدينا فرضية مسبقة (فرضية) - بأننا حصلنا على وظيفة ، وحقائق يمكن ملاحظتها - دليل (أدلة) - لا توجد مكالمة هاتفية لمدة ثلاثة أيام. الآن نريد أن نعرف احتمال أن تكون فرضيتنا صحيحة ، مع مراعاة الحقائق المقدمة. كما هو موضح أعلاه ، لدينا احتمال
P (A) = 20 ٪ .
الوقت لتحويل كل شيء رأسا على عقب! نستخدم
P ( Evidence | فرضية ) للنظر في المشكلة من الجانب الآخر ونسأل: "ما هو احتمال وقوع هذه الأحداث في الأدلة في عالم حيث فرضيتنا صحيحة؟" لذا ، إذا عدنا إلى مثالنا ، فنحن نريد أن نعرف مدى احتمال عدم قيامنا بالاتصال بنا في غضون ثلاثة أيام ، سنظل معيّنين. في الصورة أعلاه ، قمت بتمييز
P ( Evidence | Hypothesis ) على أنها "قشارة" (قشارة) ، لأن هذه الكلمة تعكس جوهر المعنى جيدًا. عندما نضربها بقيمة مسبقة ، فإنها تقلل أو تزيد من احتمال وقوع حدث ، وهذا يتوقف على ما إذا كان أي حدث يثبت فرضيتنا "ضار". في حالتنا ، كلما مرت الأيام دون اتصال ، قل احتمال استدعائنا للعمل. 3 أيام من الصمت سيئة بالفعل (فهي تقلل من احتمالنا المسبق بنسبة 60 ٪) ، في حين أن 20 يومًا دون اتصال ستدمر تمامًا الأمل في الحصول على وظيفة. وبالتالي ، كلما ازداد عدد الأحداث التي تتراكم فيها الأدلة (تمر أيام أكثر دون مكالمة هاتفية) ، كلما قلّ حجم المتسلق من الاحتمال. المتسلق عبارة عن آلية تستخدمها نظرية بايز لضبط حكمنا.
هناك شيء واحد كافحتُه في النسخة الأصلية من هذا المقال. كان هذا هو السبب في أن تقييم
P ( Evidence | Hypothesis ) أسهل من P (فرضية | Evidence). والسبب في ذلك هو أن
P ( Evidence | Hypothesis ) هي مجال محدود أكثر بكثير للحكم على العالم. تضييق النطاق ، ونحن تبسيط المهمة. يمكننا تشبيه النار والدخان ، حيث النار هي فرضيتنا ، ومراقبة الدخان هي حدث يثبت وجود النار. يصعب تقييم
P (fire | smoke) ، لأن الكثير من الأشياء يمكن أن تسبب دخان - عادم السيارات ، والمصانع ، والشخص الذي يقلي الهامبرغر على الفحم. في الوقت نفسه ،
P (smoke | fire) أسهل في التقييم ، لأنه في عالم نشبت فيه النار ، سيكون هناك بالتأكيد دخان.
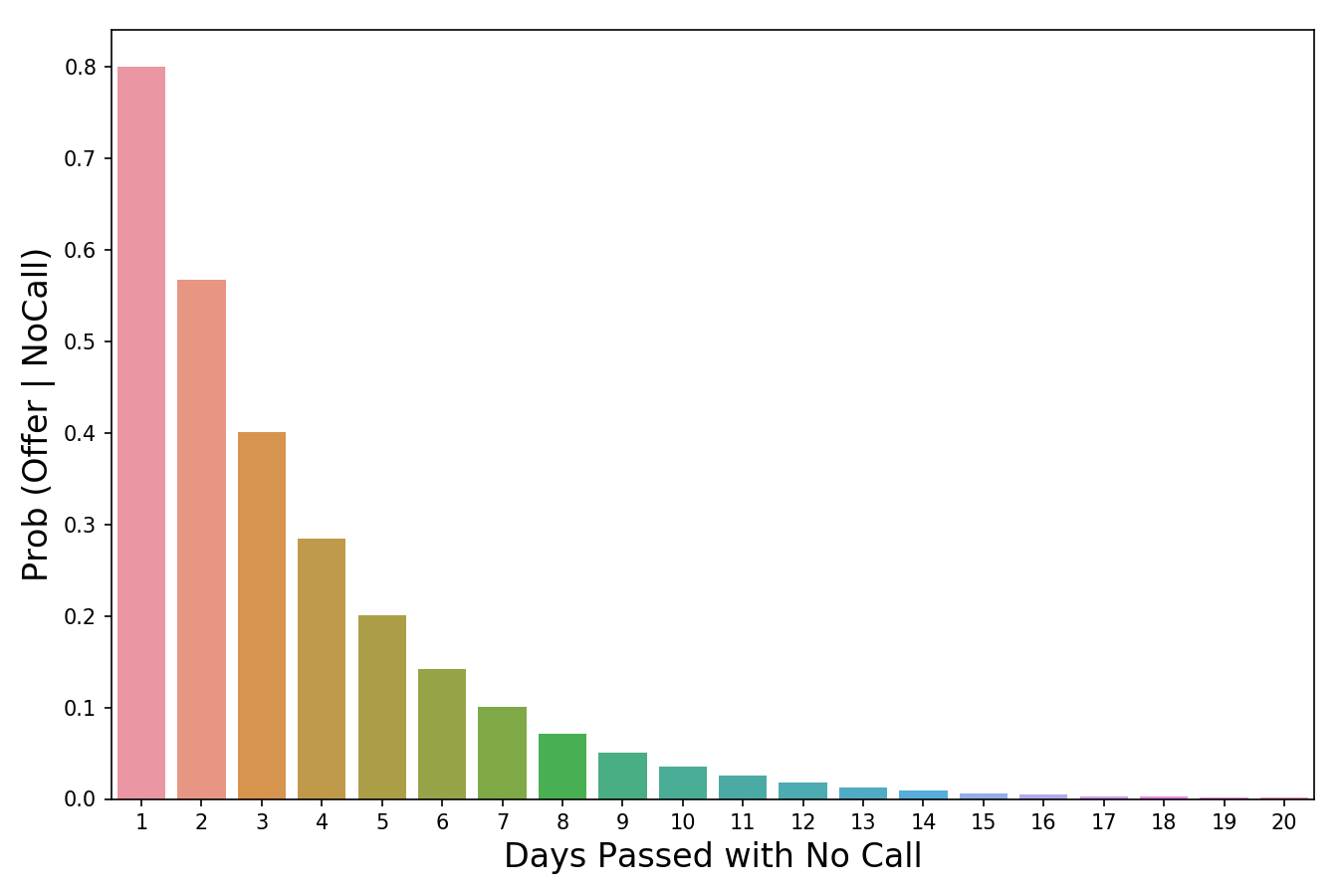تنخفض قيمة الاحتمال مع مرور عدد الأيام دون اتصال.الجزء الأخير من الصيغة ،
P (B) أو
P ( Evidence ) ، هو المُطبيع. كما يوحي الاسم ، والغرض منه هو تطبيع المنتج من الاحتمال المسبق وقشارة. إذا لم يكن هناك منظم ، فسيكون لدينا التعبير التالي:
لاحظ أن منتج الاحتمال المسبق والقشارة يساوي احتمال المفصل. ولأن أحد مكونات
P ( الإثبات ) فيه ، فإن احتمال المفصل سوف يتأثر بالوتيرة الصغيرة للأحداث.
هذه مشكلة لأن الاحتمال المشترك يمثل قيمة تشمل جميع دول العالم. لكننا لسنا بحاجة إلى جميع الولايات ، بل نحتاج فقط إلى تلك الدول التي تم تأكيدها من خلال دليل الأحداث. وبعبارة أخرى ، نحن نعيش في عالم حيث الأحداث - الأدلة قد حدثت بالفعل ، وعددهم لم يعد مهمًا (لذلك ، نحن لا نريدهم أن تؤثر على حساباتنا من حيث المبدأ). قسمة المنتج على الاحتمال المسبق والقشارة على
P ( الإثبات ) يغيره من الاحتمال المشترك إلى الشرطي (الخلفي). يأخذ الاحتمال الشرطي في الحسبان فقط دول العالم التي حدث فيها إثبات للأحداث ، وهو بالضبط ما نحققه.
من وجهات النظر الأخرى التي يمكننا من خلالها النظر في سبب تقسيم المتسلق إلى مُطوِّل هو الإجابة عن سؤالين مهمين - وتجمع علاقتهما بين هذه المعلومات. لنأخذ مثالا على مقالتي
بايز الأخيرة. لنفترض أننا نحاول معرفة ما إذا كان الحيوان المُلاحظ هو قطة ، بناءً على علامة واحدة - البراعة. كل ما نعرفه هو أن الحيوان الذي نتحدث عنه رشيق.
- يخبرنا Scaler النسبة المئوية للقطط التي تتميز بالبراعة. يجب أن تكون هذه القيمة عالية جدًا ، على سبيل المثال 0.90.
- يخبرنا عامل التطبيع عن النسبة المئوية للمصائد الحيوانية من حيث المبدأ. يجب أن تكون هذه القيمة متوسطة ، على سبيل المثال 0.50.
- تشير النسبة 0.90 / 0.50 = 1.8 إلى أنك بحاجة إلى تغيير الاحتمال المسبق ، لأنه إذا فكرت سابقًا بخلاف ذلك ، فقد حان الوقت لتغيير رأيك ، نظرًا لأنك تتعامل على الأرجح مع قطة. السبب وراء التفكير في ذلك هو أننا لاحظنا بعض الأدلة على أن الحيوان رشيق. ثم وجدنا أن نسبة القطط حاذق أكبر من نسبة الحيوانات حاذق بشكل عام. بالنظر إلى أننا لا نعرف في الوقت الحالي سوى مثل هذا الدليل وليس أكثر من ذلك ، سيكون من الحكمة إعادة النظر في معتقداتنا في اتجاه الأفكار التي ما زلنا نراقب القط.
لتلخيص
الآن بعد أن عرفنا كيف نفسر كل جزء من الصيغة ، يمكننا أخيرًا تجميع كل شيء معًا وننظر إلى ما حدث:
- بعد المقابلة مباشرة ، نقوم بإنشاء احتمال مسبق - فرصة توظيفنا هي 20٪.
- كلما زاد عدد الأيام التي تمر دون مكالمة ، قل احتمال توظيفنا. على سبيل المثال ، بعد ثلاثة أيام بدون مكالمة ، نعتقد أنه في عالم يمكننا فيه الحصول على هذه الوظيفة ، هناك فرصة بنسبة 40٪ فقط لكي تنسحب الشركة لفترة طويلة قبل أن تتصل بك. اضرب المتسلق باحتمال مسبق واحصل على 20٪ * 40٪ = 8٪
- أخيرًا ، نحن نفهم أن 8٪ تم حسابها لجميع الظروف التي قد يكون العالم فيها. لكننا نشعر بالقلق فقط بشأن الظروف التي لم يتم الاتصال بنا لمدة ثلاثة أيام. من أجل العمل فقط مع هذه الشروط ، فإننا نأخذ 90٪ من الاحتمال المسبق بعدم وجود مكالمة في غضون ثلاثة أيام ونحصل على منظم. نقسم 8٪ المستلمة مسبقًا على المقيس 8٪ / 90٪ = 8.9٪ ونحصل على الإجابة النهائية. إجمالي ، في جميع ظروف العالم ، إذا لم تتلقَ مكالمة من الشركة في غضون ثلاثة أيام ، فإن احتمال الحصول على وظيفة هو 8.9٪ فقط.
آمل أن يكون هذا المقال مفيدًا لك!