👹 🔩 🕞 ينتقل في رسومات ثلاثية الأبعاد ، الخيار الأكثر آلية 💧 🈂️ 🤳

منذ حوالي شهر ، بدأت أتعلم بيثون من كتاب داوسون واستيقظت بعمق في عملية كتابة لعبتي تحت لعبة الأقزام. لقد كانت المعارف التقليدية أكثر واعدة في جعل لعبة ذات رسومات ثلاثية الأبعاد زائفة عن طريق حشو الأسطح المحفوظة للخطوط ثلاثية الأبعاد في نقوش متحركة. سأكتب عن الأخير.

لذلك ، هناك مضلعات (من الأسهل العمل مع رباعي الزوايا) نرغب في تمديد الأسطح المكعبة بحيث تتسق مع بعضها بسلاسة تامة - هذه الأسطح هي شرائح.

من الأكثر ملاءمة تقديم شريحة من أجل مضلع واحد كدالة

g (u ، v) = v c d o t g_{1} (u) + (1 - v) c d o t g_{2} (u) + u c d o t g_{3} (v) + (1 - u) c d o t g_{4} (v) (1)

$g (u، v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (1-u) \ cdot g_4 (v) (1)$

هنا

g_{1} ، g_{2} ، g_{3} ، g_{4}

$g_1 ، g_2 ، g_3 ، g_4$

- كثير الحدود مكعبة تلبي بعض الشروط الحدودية (في الشكل أدناه - منحنيات الضوء الأخضر والأحمر ، والظروف المشتقة الأولية - ناقلات أرجواني وأزرق) ؛ تختلف u و v من 0 إلى 1.

في هذا التفسير ، تُفقد بعض الدرجات (نتاج 2 و 3 درجات من المعلمات) ، ولكن يمكن العثور على معاملات كثير الحدود من خلال تحديد 12 متجه فقط من الحالات الأولية (4 نقاط مضلع وناقلات مشتقة فيما يتعلق u و v لكل نقطة). عند التقاطعات ، تتزامن الخطوط في حالة تعيين شروط أولية مماثلة للمضلعات المجاورة (يجب أن تكون الموجات المشتقة متداخلة ، ويمر السطح عبر نفس نقاط المضلع).

مشكلة واحدة - مشتق مع مثل هذا البيان للمشكلة على الحدود بأكملها قد لا تتزامن - سيكون هناك القطع الأثرية الصغيرة في المفاصل. يمكنك التفكير في 4 شروط أخرى لتصحيح ذلك وإضافة مصطلح آخر بعناية إلى الصيغة

u c d o t v c d o t (u - 1) c d o t (v - 1) c d o t g_{5} (u ، v)

$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u، v)$

التي لا تفسد الحدود ، ولكن هذا هو موضوع لمقال منفصل.

البديل هو Bezier ، لكنه يقترح تعيين 16 معلمة من المعنى الرياضي غير المفهوم (بالنسبة لي) ، أي من المفترض أن الفنان سيعمل بيديه. هذا ليس مناسبًا جدًا بالنسبة لي ، لذا فإن الدراجة ذات العكازات تتبعها.

يتم حساب المعاملات (1) بسهولة من خلال إيجاد المصفوفة العكسية لمصفوفة القيم والمشتقات في الزوايا والضرب بشروط الإدخال (ثلاث مرات ، لكل إحداثي). المصفوفة قد تكون هذه:

النص المخفي

[[1 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0] ، #g (0،0)
[1 ، 0 ، 0 ، 0 ، 1 ، 0 ، 0 ، 0 ، 1 ، 0 ، 1 ، 0] ، #g (1،0)
[1 ، 1 ، 1 ، 1 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0] ، #g (0،1)
[1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1 ، 1] ، # ز (1،1)
[0 ، 0 ، 0 ، 0 ، 1 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0] ، # dg / du (0،0)
[0 ، 0 ، 0 ، 0 ، 1 ، 0 ، 0 ، 0 ، 2 ، 0 ، 3 ، 0] ، # dg / du (1،0)
[0 ، 0 ، 0 ، 0 ، 1 ، 1 ، 1 ، 1 ، 0 ، 0 ، 0 ، 0] ، # dg / du (0،1)
[0 ، 0 ، 0 ، 0 ، 1 ، 1 ، 1 ، 1 ، 2 ، 2 ، 3 ، 3] ، # dg / du (1،1)
[0 ، 1 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0] ، # dg / dv (0،0)
[0 ، 1 ، 0 ، 0 ، 0 ، 1 ، 0 ، 0 ، 0 ، 1 ، 0 ، 1] ، # dg / dv (1،0)
[0 ، 1 ، 2 ، 3 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0 ، 0] ، # dg / dv (0،1)
[0 ، 1 ، 2 ، 3 ، 0 ، 1 ، 2 ، 3 ، 0 ، 1 ، 0 ، 1]] # dg / dv (1،1)

NumPy يقوم بعمل ممتاز من هذا.

يبقى سؤال واحد - أين يمكن الحصول على ناقلات المشتقات. من المفترض أنه يجب اختيارهم بطريقة أو بأخرى بناءً على موضع النقاط المجاورة (للمضلع) ولأسباب نعومة.
بالنسبة لي شخصيا ، كان لا يزال من البديهي تماما كيفية التعامل مع طول ناقل المشتق. الاتجاه مفهوم ، ولكن طول؟

نتيجة لذلك ، تم إنشاء الخوارزمية التالية:

1. في المرحلة الأولى ، يحدث بعض تصنيف النقاط. في الرسم البياني (الذي تحدده نقاط المضلعات ووصلاتها) ، يتم البحث عن دورات الطول 4 وتخزينها ، وبالإضافة إلى ذلك ، يتم تسجيل الجيران الأكثر ملاءمة لدور تمديد حواف المضلع (يتم تحديده مسبقًا أي الحواف تتوافق مع تغيير المعلمة u وتلك التي تتوافق مع v). فيما يلي جزء من التعليمات البرمجية التي تبحث وتصنف وتذكر الجيران عن النقطة صفر من الدورة:

النص المخفي

"""   : cykle[5] cykle[7] cykle[4]--cykle[0] --u-- cykle[1]-cykle[6] |v |v cykle[10]-cykle[3] --u-- cykle[2]-cykle[8] cykle[11] cykle[9] """ sosed = [] for i in range(0, N): if self.connects[i][ind] == 1 and i != cykle[0] and i != cykle[1] and i != cykle[3]: sosed += [i] #    ... if(len(sosed) < 2): continue #    else: #      cykle[0] vs0c3 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[3]]) vs1c1 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[1]]) #        vs0c1 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[1]]) vs1c3 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[3]]) Rvsc = [ScalMult(vs0c3,vs0c3),ScalMult(vs1c1,vs1c1),ScalMult(vs0c1,vs0c1),ScalMult(vs1c3,vs1c3) ] n1 = Rvsc.index(max(Rvsc)) if n1 < 2: cykle += [sosed[1],sosed[0]] #  u   v else: cykle += [sosed[0],sosed[1]]

علاوة على ذلك ، عند إنشاء الشريحة ، يتم تحديد المشتق على طول الحافة (على سبيل المثال ، فيما يتعلق بالمعلمة u) عند نقطة المضلع بناءً على موقع نقطتين من الحافة ونقطة متجاورة واحدة (دعها تكون النقاط vec1 و vec2 و vec3 ؛ والنقطة التي يتم البحث فيها عن المشتق هي الثانية).

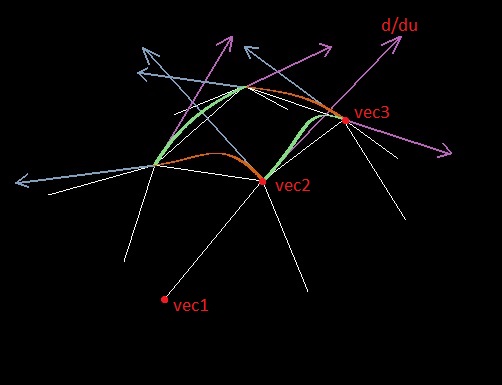
في البداية ، حاولت استخدام المتجه الطبيعي vec3 - vec1 (مثلما قمت بتطبيق نظرية لاغرانج) لهذا الدور ، ولكن نشأت المشكلات على وجه التحديد مع طول المتجه المشتق - مما جعله ثابتًا كان فكرة سيئة.

الانحدار الغنائي:

للحصول على رسم توضيحي صغير لما هو متجه المشتق في الإصدار حدودي ، ننتقل إلى تشبيه بسيط ثنائي الأبعاد - هنا قطعة من قوس دائري:

g (u) = (R s i n (u p i / 2) ، R c o s (u p i / 2))

$g (u) = (Rsin (u \ pi / 2) ، Rcos (u \ pi / 2))$

g^{'} (u) = (R p i / 2 c d o t c o s (u p i / 2) ، - R p i / 2 c d o t s i n (u p i / 2))

$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2) ، -R \ pi / 2 \ cdot sin (u \ pi / 2))$

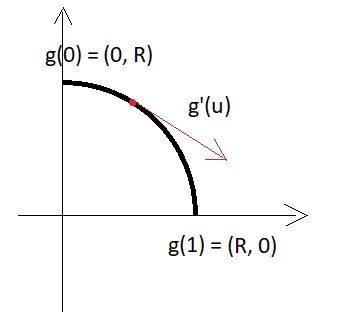
أي معامل المشتق = R * pi / 2 ، وبصفة عامة ، يعتمد على حجم قطعة القوس ، التي وضعناها من خلال المعلمة.

ما يجب القيام به الآن؟ لقد ورث لنا ليو تولستوي أن كل شيء مستدير = جيد ، لذلك ، إذا وضعنا المشتق عند نقطة كما لو كنا نرغب في بناء قوس هناك ، فسوف نحصل على منحنى جميل ناعم.

نهاية الاستطراد.

المرحلة الثانية من البحث المشتق:

2. من خلال نقاطنا الثلاث vec1 ، vec2 ، vec3 نقوم ببناء طائرة ، في هذه الطائرة نبحث عن دائرة تمر عبر النقاط الثلاث. سيتم توجيه المشتق المرغوب على طول المماس إلى الدائرة عند النقطة vec2 ، وينبغي أن يكون معامل متجه المشتق مساويًا لمنتج نصف قطر الدائرة وزاوية القطاع ، والتي تشكل نقطتين من وجه المضلع (على غرار القياس المسطح البسيط من الاستدلال الغنائي).

g^{'} = R c d o t p h i

$g '= R \ cdot \ phi$

يبدو أن كل شيء بسيط ، فيما يلي رمز الوظيفة ، على سبيل المثال (يتم استخدام NumPy مرة أخرى):

ليس رمز ، ولكن ...

 def create_dd(vec1, vec2, tuda, vec3): """     1-2       3   == 1""" #0.         -         :( vecmult = VecMult(MinusVecs(vec2,vec1),MinusVecs(vec3,vec1)) #  vec2-vec1 x vec3 - vec1 if vecmult[0]*vecmult[0] + vecmult[1]*vecmult[1] + vecmult[2]*vecmult[2] < 0.000001: #  0 if tuda == 1: return NormVec(MinusVecs(vec3,vec2)) else: return NormVec(MinusVecs(vec1,vec2)) #1.   ,     #           2   M = np.zeros((3,3),float) C = np.zeros((3,1),float) M[0][0] = 2*vec2[0] - 2*vec1[0] M[0][1] = 2*vec2[1] - 2*vec1[1] M[0][2] = 2*vec2[2] - 2*vec1[2] C[0] = -vec1[0]*vec1[0] - vec1[1]*vec1[1] - vec1[2]*vec1[2] + vec2[0]*vec2[0] + vec2[1]*vec2[1] + vec2[2]*vec2[2] M[1][0] = 2*vec3[0] - 2*vec2[0] M[1][1] = 2*vec3[1] - 2*vec2[1] M[1][2] = 2*vec3[2] - 2*vec2[2] C[1] = -vec2[0]*vec2[0] - vec2[1]*vec2[1] - vec2[2]*vec2[2] + vec3[0]*vec3[0] + vec3[1]*vec3[1] + vec3[2]*vec3[2] #   ,   4     M[2][0] = vecmult[0] M[2][1] = vecmult[1] M[2][2] = vecmult[2] C[2] = vecmult[0]*vec1[0] + vecmult[1]*vec1[1] + vecmult[2]*vec1[2] # M *    = C Mobr = np.linalg.inv(M) Rvec = np.dot(Mobr,C) res = NormVec(VecMult(MinusVecs(Rvec,vec2), vecmult)) #    ka #R = math.sqrt((Rvec[0]-vec1[0])**2 + (Rvec[1]-vec1[1])**2 + (Rvec[2]-vec1[2])**2) #   = 3.14*2*asin(l/(2*R))/180 * R,      l  ,    l = 1.2*math.sqrt((vec1[0]-vec2[0])**2 + (vec1[1]-vec2[1])**2 + (vec1[2]-vec2[2])**2) if ScalMult(res, MinusVecs(vec2, vec1)) > 0: #     return MultVxC(res, tuda*l) else: return MultVxC(res, -tuda*l)

حسنا ، بشكل عام ، كل شيء يعمل بطريقة ما. من أجل العرض التوضيحي ، أخذت مكعبًا 5 × 5 × 5 وقمت بتغيير موضع النقاط باستخدام أداة عشوائية:

GIF ، 8 ميغابايت

ينتقل في رسومات ثلاثية الأبعاد ، الخيار الأكثر آلية

More articles: