لماذا نحتاج يتراوح من C ++ 20 في كسارة بسيطة؟

في الآونة الأخيرة ، تمت مناقشة النطاقات التي يجب تضمينها في معيار C ++ 20 كثيرًا ، بما في ذلك على Habré ( مثال حيث توجد العديد من الأمثلة ). هناك ما يكفي من النقاد لفترات ، يقولون ذلك

• فهي مجردة للغاية وتحتاج فقط لرمز مجردة للغاية
• قراءة التعليمات البرمجية معهم يزداد سوءًا فقط
• فترات تبطئ رمز

دعونا نرى تماما العمال والفلاحين مهمة عملية ، من أجل فهم ما إذا كانت هذه الانتقادات صحيحة وهل صحيح أن إريك نيبلر قد تعرض للعض من قبل بارتوش ميلوسكي ويكتب المدى 3 فقط مع اكتمال القمر .

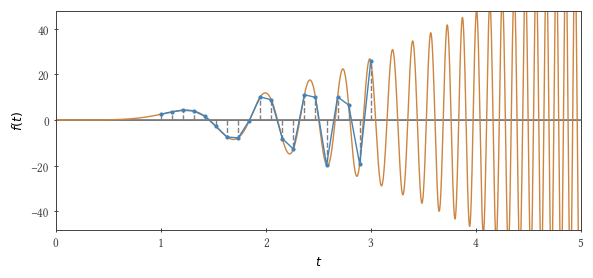
سنقوم بدمج الوظيفة التالية باستخدام طريقة شبه منحرف:$$ $ inline $ f (t) = 3 t ^ 2 \ sin t ^ 3 $ inline $ تتراوح من صفر إلى$$ $ inline $ \ tau $ inline $ . إذا$$ $ inline $ \ tau ^ 3 / \ pi $ inline $ يساوي عدد فردي ، ثم التكامل هو 2.

لذلك ، المشكلة: نكتب نموذجًا أوليًا للدالة التي تحسب التكامل بواسطة طريقة شبه المنحرف . يبدو ، للوهلة الأولى ، أن هناك حاجة إلى التجريد هنا ، ولكن السرعة مهمة. في الواقع ، هذا ليس صحيحا تماما. بالنسبة للعمل ، غالبًا ما يجب عليّ كتابة "كسارات الأرقام" ، المستخدم الرئيسي هو نفسي. لذلك يجب علي أيضًا دعم الأخطاء والتعامل معها (لسوء الحظ زملائي - ليس فقط أنا دائمًا). ويحدث أيضًا أن بعض التعليمات البرمجية لا يتم استخدامها ، على سبيل المثال ، لمدة عام ، ثم ... بشكل عام ، يلزم أيضًا كتابة الوثائق والاختبارات.

ما هي الحجج التي يجب أن تحتوي عليها وظيفة التكامل؟ وظيفة متكاملة وشبكة (مجموعة من النقاط$$ $ inline $ t_1 ، t_2 ، t_3 ... $ inline $ تستخدم لحساب لا يتجزأ). وإذا كان كل شيء واضحًا مع الوظيفة المدمجة (ستكون std::function هنا فقط) ، فما الشكل الذي ينبغي أن تنتقل به الشبكة؟ لنرى.

خيارات

بادئ ذي بدء - بحيث يكون هناك شيء يمكن مقارنته بالأداء - سنقوم بكتابة حلقة بسيطة بخطوة زمنية ثابتة:

 // trapezoidal rule of integration with fixed time step; // dt_fixed is the timestep; n_fixed is the number of steps double integrate() { double acc = 0; for(long long i = 1; i < n_fixed - 1; ++i) { double t = dt_fixed * static_cast<double>(i); acc += dt_fixed * f(t); } acc += 0.5 * dt_fixed * f(0); acc += 0.5 * dt_fixed * f(tau); return acc; } 

عند استخدام هذه الدورة ، يمكنك تمرير الوسيطات إلى الدالة بداية ونهاية الفاصل الزمني للتكامل ، وكذلك عدد النقاط لهذا التكامل نفسه. توقف - يحدث أسلوب شبه المنحرف أيضًا بخطوة متغيرة ، وتطلب وظيفتنا القابلة للتكامل ببساطة استخدام خطوة متغيرة! فليكن ذلك ، فلنحصل على معلمة أخرى ($$ $ مضمنة $ b $ مضمنة $ ) للتحكم في "اللاخطية" والسماح لخطواتنا ، على سبيل المثال ، كما يلي:$$ $ inline $ \ Delta t (t) = \ Delta t_0 + bt $ inline $ . ربما يتم استخدام هذا النهج (إدخال معلمة رقمية إضافية) في مليون مكان ، على الرغم من أنه يبدو أن عيبه يجب أن يكون واضحًا للجميع. وإذا كان لدينا وظيفة مختلفة؟ وإذا كنا بحاجة إلى خطوة صغيرة في مكان ما في منتصف الفاصل العددي لدينا؟ ولكن ماذا لو كانت وظيفة قابلة للتكامل لها عدة ميزات؟ بشكل عام ، يجب أن نكون قادرين على نقل أي شبكة. (ومع ذلك ، في الأمثلة ، حتى النهاية ، سوف "ننسى" طريقة شبه منحرف حقيقية ، وللبساطة ، سننظر في نسخته بخطوة ثابتة ، مع مراعاة أن الشبكة يمكن أن تكون تعسفية).

نظرًا لأن الشبكة يمكن أن تكون موجودة ، فلنقل قيمها$$ $ inline $ t_1 ، t_2 ، ... $ inline $ ملفوفة في std::vector .

 // trapezoidal rule of integration with fixed time step double integrate(vector<double> t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } 

هناك أكثر من كافية من المجتمعات في هذا النهج ، ولكن ماذا عن الأداء؟ مع استهلاك الذاكرة؟ إذا تم تلخيص كل شيء في وقت سابق على المعالج ، فعلينا الآن أن نملأ منطقة الذاكرة أولاً ، ثم نقرأ منها. والتواصل مع الذاكرة شيء بطيء إلى حد ما. والذاكرة لا تزال غير المطاط ( والسيليكون ).

دعونا ننظر إلى جذر المشكلة. ماذا يحتاج الشخص ليكون سعيدا؟ بتعبير أدق ، ما الذي تحتاجه دورتنا (القائمة على النطاق للحلقة)؟ أي حاوية بها متكررات start begin() و end() و ++ و * و != عوامل تشغيل للمكررات. لذلك سوف نكتب.

 //   ,    ,      template <typename T> double integrate(T t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } // ... //      class lazy_container { public: long long int n_nodes; lazy_container() { n_nodes = n_fixed; } ~lazy_container() {} class iterator { public: long long int i; // index of the current node iterator() { i = 0; } ~iterator() {} iterator& operator++() { i+= 1; return *this; } // ! bool operator!=(const iterator& rhs) const { return i != rhs.i; } double operator* () const { return dt_fixed * static_cast<double>(i); } }; iterator begin() { return iterator(); } iterator end() { iterator it; it.i = n_nodes; return it; } }; // ... //      lazy_container t_nodes; double res = integrate(t_nodes); 

نحن نحسب قيمة جديدة هنا.$$ $ inline $ t_i $ inline $ بناء على الطلب ، كما فعلنا في حلقة بسيطة. لا توجد ذاكرة الوصول ، ويؤمل أن المجمعين الحديثة سوف تبسيط التعليمات البرمجية بكفاءة عالية. في الوقت نفسه ، لم يتغير رمز الدالة المدمجة كثيرًا ، ولا يزال بإمكانه هضم std::vector .

أين هي المرونة؟ في الواقع ، يمكننا الآن كتابة أي وظيفة في مشغل ++ . وهذا يعني أن هذا النهج يسمح ، في الواقع ، بنقل وظيفة بدلاً من معلمة رقمية واحدة. يمكن أن تكون الشبكة التي تم إنشاؤها على الطاير موجودة ، ونحن أيضًا (على الأرجح) لا نفقد الأداء. ومع ذلك ، فإن كتابة lazy_container جديدة في كل مرة لتشويه الشبكة بطريقة أو بأخرى بطريقة جديدة لا تشعر بها على الإطلاق (إنها 27 سطرًا!). بالطبع ، يمكنك جعل الوظيفة مسؤولة عن إنشاء الشبكة كمعلمة لدالة التكامل الخاصة بنا ، lazy_container أيضًا ، أي ، عفواً ، قم lazy_container .

أنت تسأل - ثم هل سيكون هناك خطأ مرة أخرى؟ نعم! أولاً ، سيكون من الضروري نقل عدد نقاط التكامل بشكل منفصل ، مما قد يتسبب في حدوث خطأ. ثانياً ، يجب دعم الدراجة التي تم إنشاؤها وغير القياسية وقد يتم تطويرها بواسطة شخص ما. على سبيل المثال ، هل يمكنك أن تتخيل على الفور كيف ، من خلال هذا النهج ، أن تؤلف مُجمعًا للوظائف في مشغل ++ ؟

C ++ لأكثر من 30 سنة. العديد من الأطفال في هذه السن لديهم أطفال بالفعل ، ولا يحتوي C ++ على حاويات / كسرات قياسية. كابوس! لكن كل شيء (بمعنى التكرار ، وليس الأطفال) سيتغير في وقت مبكر من العام المقبل - سيتضمن المعيار (ربما جزئيًا) مكتبة range-v3 ، التي طورها إريك نيبلر لعدة سنوات. سوف نستخدم أعمال ثمارها. رمز يقول كل شيء لنفسه:

 #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... auto t_nodes = ranges::v3::iota_view(0, n_fixed) | ranges::v3::views::transform( [](long long i){ return dt_fixed * static_cast<double>(i); } ); double res = integrate(t_nodes); 

وظيفة التكامل لا تزال هي نفسها. هذا هو ، فقط 3 خطوط لحل مشكلتنا! هنا iota_view(0, n) كسولًا (نطاقًا ، كائنًا يُغلف البداية والنهاية المعممة ؛ والنطاق البطيء هو طريقة عرض) ، والتي ، عند التكرار في كل خطوة ، تحسب الرقم التالي في النطاق [0 ، n). من المضحك أن الاسم ι (الحرف iota اليوناني) يشير منذ 50 عامًا إلى لغة APL. عصا | يسمح لك بكتابة خطوط أنابيب من المعدلات الفاصلة ، transform ، في الواقع ، هو مثل هذا التعديل الذي ، باستخدام وظيفة بسيطة lambda ، يحول سلسلة من الأعداد الصحيحة إلى سلسلة$$ $ inline $ t_1 ، t_2 ، ... $ inline $ . كل شيء بسيط ، كما هو الحال في حكاية خرافية هاسكل.

ولكن كيف تجعل خطوة متغيرة؟ كل شيء بسيط مثل:

 #include <range/v3/view/drop.hpp> #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... // trapezoidal rule of integration; step size is not fixed template <typename T> double integrate(T t_nodes) { double acc = 0; double t_prev = *(t_nodes.begin()); double f_prev = f(t_prev); for (auto t: t_nodes | ranges::v3::views::drop(1)) { double f_curr = f(t); acc += 0.5 * (t - t_prev) * (f_curr + f_prev); t_prev = t; f_prev = f_curr; } return acc; } //... auto step_f = [](long long i) { if (static_cast<double>(i) <= 1 / a) { return pow(2 * M_PI, 1/3.0) * a * static_cast<double>(i); } else { return tau * pow(static_cast<double>(i) / static_cast<double>(n), 1/3.0); } }; auto t_nodes = ranges::v3::iota_view(0, n) | ranges::v3::views::transform(step_f); double res = integrate(t_nodes); 

لاحظ القارئ اليقظ أنه في مثالنا ، سمحت لنا الخطوة المتغيرة بتقليل عدد نقاط الشبكة بعامل من ثلاثة ، بالإضافة إلى ذلك ، هناك نفقات ملحوظة للحوسبة$$ $ inline $ t_i $ inline $ . ولكن إذا أخذنا آخر$$ $ inline $ f (t) $ inline $ ، يمكن أن يتغير عدد النقاط أكثر من ذلك بكثير ... (ولكن المؤلف أصبح كسولًا بالفعل).

لذلك توقيت

لدينا الخيارات التالية:

• v1 - حلقة بسيطة
• الإصدار 2 -$$ $ inline $ t_i $ inline $ تكمن في std::vector
• v3 - مؤقتة lazy_container مع مكرر مؤقت
• v4 - فواصل زمنية من C ++ 20 (نطاقات)
• v5 - يتراوح مرة أخرى ، ولكن هنا فقط يتم كتابة طريقة شبه المنحرف باستخدام درجة متغيرة

إليك ما اتضح (بالثواني) لـ$$ $ inline $ \ tau = (10 \، 000 \، 001 \ times \ pi) ^ {1/3} $ inline $ ، بالنسبة إلى الإصدار 8.0.0.0 من g ++ و clang ++ 8.0.0 على وحدة المعالجة المركزية Intel® Xeon® CPU® X5550 (عدد الخطوات$$ $ مضمنة $ 1.5 \ مرة 10 ^ 8 $ مضمنة ، باستثناء الإصدار 5 ، حيث تكون الخطوات أقل بثلاث مرات (تختلف نتيجة العمليات الحسابية بكل الطرق عن الاثنين بنسبة لا تزيد عن 0.07):

بشكل عام ، ذبابة ذبابة عبر الميدان ، وجدت ذبابة عملة!

يؤدي

حتى في مهمة بسيطة للغاية ، تبين أن النطاقات كانت مفيدة للغاية: بدلاً من التعليمات البرمجية ذات التكرارات ذاتية الصنع على أكثر من 20 سطرًا ، كتبنا 3 أسطر ، مع عدم وجود مشاكل في إمكانية قراءة التعليمات البرمجية أو أدائها.

بالطبع ، إذا احتجنا (من أجل) الأداء النهائي في هذه الاختبارات ، فسنضطر إلى الحصول على أقصى استفادة من المعالج ومن الذاكرة عن طريق كتابة شفرة متوازية (أو كتابة إصدار تحت OpenCL) ... وأيضًا ، ليس لدي أي فكرة عما سيحدث إذا كتبت سلاسل طويلة جدا من المعدلات. هل من السهل تصحيح وقراءة رسائل المترجم عند استخدام النطاقات في المشاريع المعقدة. سيتم تجميع زيادة الوقت. آمل أن يكتب شخص ما عن هذا المقال.

عندما كتبت هذه الاختبارات ، لم أكن أعرف بنفسي ما الذي سيحدث. الآن أعرف أن النطاقات تستحق بالتأكيد أن يتم اختبارها في مشروع حقيقي ، في الظروف التي تنوي استخدامها.

ذهبت إلى البازار لشراء السماور.

روابط مفيدة

مجموعة V3 المنزل

الوثائق ودراسات الحالة v3

كود من هذه المادة على جيثب

قوائم في haskell ، للمقارنة

شكر

شكرا فادي للمساعدة في كتابة كل هذا!

PS

آمل أن يعلق شخص ما على مثل هذه الأمور الشاذة: 1) إذا كنت تأخذ فترة التكامل أصغر بعشر مرات ، فعندئذٍ في My Xeon ، يكون v2 أسرع بنسبة 10٪ من v1 ، و v4 أسرع بثلاث مرات من v1. ب) برنامج التحويل البرمجي Intel (icc 2019) أحيانًا في هذه الأمثلة ، يجعل الشفرة أسرع مرتين من المترجمة g ++. يتم توجيه اللوم؟ هل يمكن إجبار g ++ على فعل الشيء نفسه؟