مقدمة إلى التبعيات الوظيفية

في هذه المقالة سوف نتحدث عن التبعيات الوظيفية في قواعد البيانات - ما هي ، وأين يتم تطبيقها وما هي الخوارزميات الموجودة للبحث عنها.

سننظر في التبعيات الوظيفية في سياق قواعد البيانات العلائقية. التحدث بوقاحة شديدة ، في مثل هذه قواعد البيانات يتم تخزين المعلومات في شكل جداول. علاوة على ذلك ، فإننا نستخدم مفاهيم تقريبية ، والتي في نظرية علائقية صارمة غير قابلة للتبديل: سوف نسمي الجدول نفسه علاقة ، أعمدة - سمات (مجموعة الخاصة بهم - مخطط علاقة) ، ومجموعة من قيم الصفوف على مجموعة فرعية من السمات - مجموعة.



على سبيل المثال ، في الجدول أعلاه ، (Benson، M، M organ ) هي مجموعة من الصفات (المريض ، الجنس ، الطبيب) .
بشكل أكثر رسمية ، يتم كتابة هذا على النحو التالي: $$$t_ {1}$[ المريض ، بول ، دكتور ] = (بنسون ، إم ، إم الجهاز) .
الآن يمكننا تقديم مفهوم التبعية الوظيفية (FZ):

التعريف 1. العلاقة R ترضي القانون الاتحادي X → Y (حيث X ، Y ⊆ R) إذا وفقط لأي من التلاميذ $$$t_ {1}$. $$$t_ {2}$holds يحمل R: إذا $$$t_ {1}$[X] = $$$t_ {2}$[س] ثم $$$t_ {1}$[Y] = $$$t_ {2}$[Y]. في هذه الحالة ، يقال أن X (المحدد ، أو مجموعة من السمات المميزة) يعرّف وظيفيًا Y (مجموعة تابعة).

وبعبارة أخرى ، فإن وجود القانون الاتحادي X → Y يعني أنه إذا كان لدينا اثنين من التلاميذ في R وتزامنوا مع سمات X ، فسوف يتزامنون أيضًا مع سمات Y.
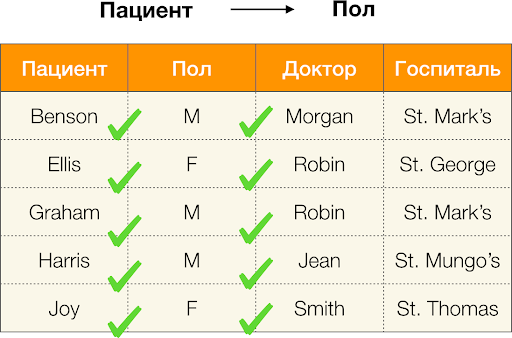
والآن بالترتيب. النظر في سمات المريض ونوع الجنس الذي نريد معرفة ما إذا كانت هناك تبعية بينهما أم لا. بالنسبة للعديد من السمات ، قد توجد التبعيات التالية:

1. المريض → الجنس
2. الجنس → المريض

وفقًا للتعريف أعلاه ، من أجل الحفاظ على التبعية الأولى ، يجب أن تتوافق قيمة واحدة فقط من عمود النوع مع كل قيمة فريدة لعمود المريض . ولجدول العينة ، هذا صحيح. ومع ذلك ، لا يعمل هذا في الاتجاه المعاكس ، أي أن التبعية الثانية لم يتم الوفاء بها ، ولا تعد سمة Paul محددًا للمريض . وبالمثل ، إذا كنت تأخذ الاعتماد على Doctor → Patient ، يمكنك أن ترى أنه قد تم انتهاكها ، لأن قيمة Robin لهذه السمة لها عدة قيم مختلفة - Ellis و Graham .

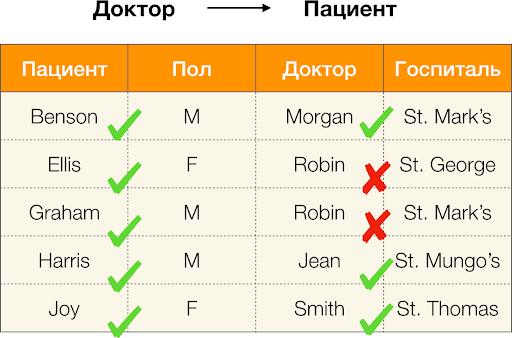
وبالتالي ، فإن التبعيات الوظيفية تجعل من الممكن تحديد العلاقات الحالية بين مجموعات سمات الجدول. من الآن فصاعدا ، سننظر في العلاقات الأكثر إثارة للاهتمام ، أو بالأحرى X → Y بحيث تكون:

• غير بديهي ، أي أن الجانب الأيمن من التبعية ليس مجموعة فرعية من اليسار (Y ̸⊆ X) ؛
• الحد الأدنى ، وهذا هو ، لا يوجد مثل هذا الاعتماد Z → Y بحيث Z ⊂ X.

كانت التبعيات التي اعتبرت حتى هذه اللحظة صارمة ، أي أنها لم تتضمن أي انتهاكات على الطاولة ، ولكن إلى جانبها هناك أيضًا تلك التي تسمح ببعض التناقض بين قيم التلاميذ. يتم وضع مثل هذه التبعيات في فصل منفصل ، يُطلق عليه تقريبي ، ويُسمح بانتهاكه على عدد معين من التلاميذ. يتم تنظيم هذا المبلغ بواسطة أقصى مؤشر خطأ emax. على سبيل المثال ، نسبة الخطأ $$$e_ {max}$= 0.01 قد يعني أن التبعية يمكن أن تنتهك بنسبة 1 ٪ من المجموعات المتاحة على مجموعة السمات المميزة. وهذا يعني أنه بالنسبة إلى 1000 سجل ، يمكن أن ينتهك 10 طلاب بحد أقصى القانون الفيدرالي. سننظر في قياس مختلف قليلاً استنادًا إلى القيم المختلفة للزوج للصفوف المقارنة. بالنسبة للاعتماد X → Y على العلاقة r ، يُعتبر كالتالي:

$$

$$e (X \ rightarrow Y، r) = \ frac {| \ {(t_1، t_2) \ in r ^ 2 \ | \ t_1 [X] = t_2 [X] \ wedge t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | - | ص |}$$

نحسب الخطأ لـ Doctor → Patient من المثال أعلاه. لدينا مجموعتان ، تختلف قيمهما في سمة المريض ، ولكن تتزامن مع الطبيب : $$$t_ {1}$[ الطبيب ، المريض ] = ( روبن ، إليس ) و $$$t_ {2}$[ الطبيب ، المريض ] = ( روبن ، جراهام ). باتباع تعريف الخطأ ، يجب أن نأخذ في الاعتبار جميع الأزواج المتعارضة ، مما يعني أنه سيكون هناك اثنان منها: ( $$$t_ {1}$. $$$t_ {2}$) وانعكاسها ( $$$t_ {2}$. $$$t_ {1}$). استبدل الصيغة واحصل على:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0.1$$

الآن دعونا نحاول الإجابة على السؤال: "لماذا كل شيء؟". في الواقع ، القوانين الاتحادية مختلفة. النوع الأول هو التبعيات التي يحددها المسؤول في مرحلة تصميم قاعدة البيانات. عادة ما تكون قليلة ، فهي صارمة ، والتطبيق الرئيسي هو تطبيع البيانات وتصميم مخطط العلاقة.

النوع الثاني هو التبعيات التي تمثل البيانات "المخفية" والعلاقات غير المعروفة سابقًا بين السمات. أي أنه لم يتم التفكير في هذه التبعيات وقت التصميم وتم العثور عليها بالفعل لمجموعة البيانات الحالية ، بحيث ، بناءً على مجموعة من القوانين الفيدرالية المحددة ، لاستخلاص أي استنتاجات حول المعلومات المخزنة. مع هذه التبعيات التي نعمل بها. انهم يعملون في مجال كامل من بيانات التعدين مع تقنيات البحث المختلفة والخوارزميات التي بنيت على أساسها. دعونا نفهم كيف يمكن أن تكون التبعيات الوظيفية التي تم العثور عليها (دقيقة أو تقريبية) في أي بيانات مفيدة.



اليوم ، تطهير البيانات هو من بين المجالات الرئيسية لاستخدام التبعية. وهو ينطوي على تطوير عمليات لتحديد "البيانات القذرة" مع تصحيحها اللاحق. الممثلون الساطعون لـ "البيانات القذرة" هم التكرارات ، أخطاء البيانات أو الأخطاء المطبعية ، القيم المفقودة ، البيانات القديمة ، المساحات الإضافية وما شابه.

مثال على خطأ في البيانات:



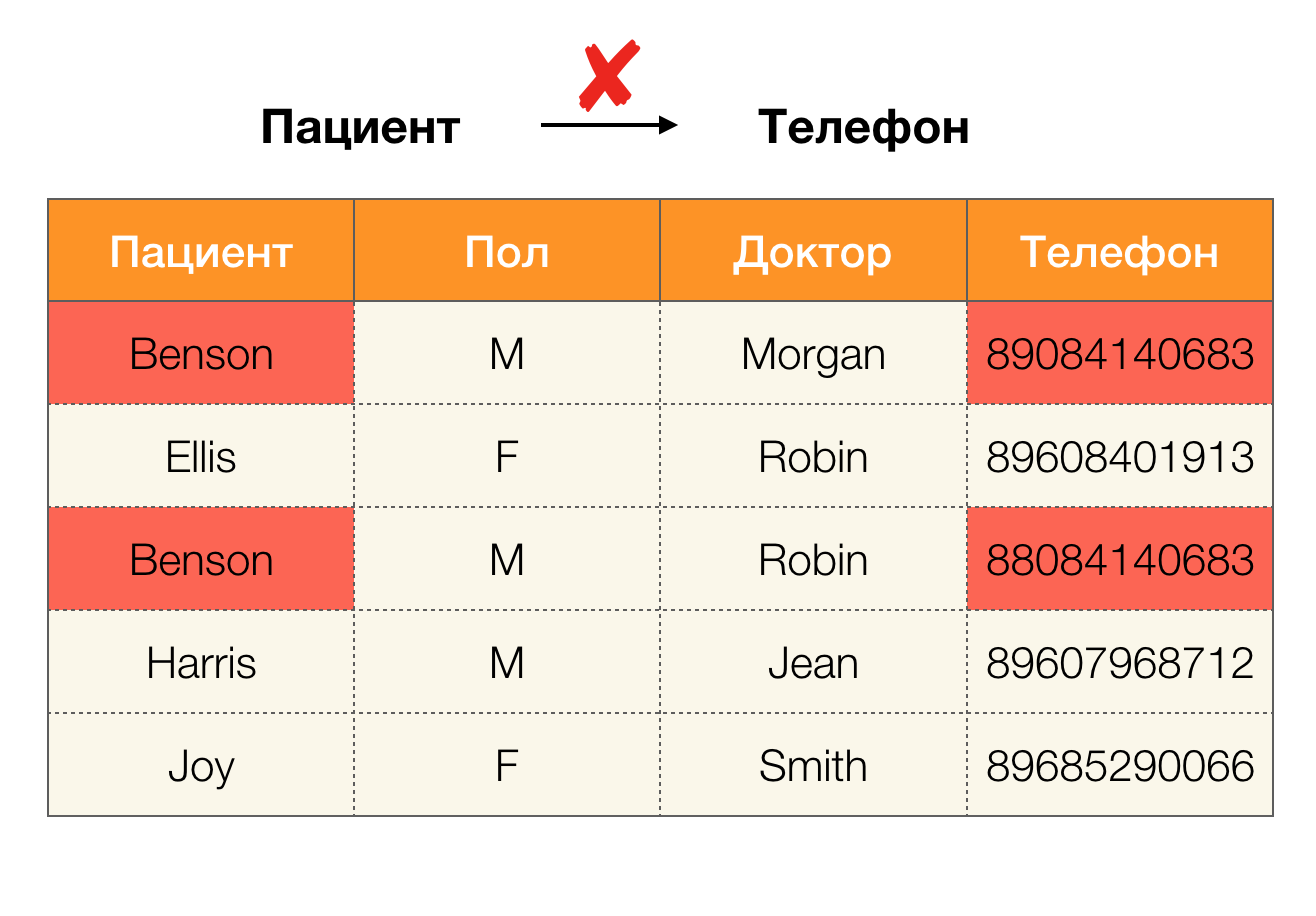
مثال التكرارات في البيانات:



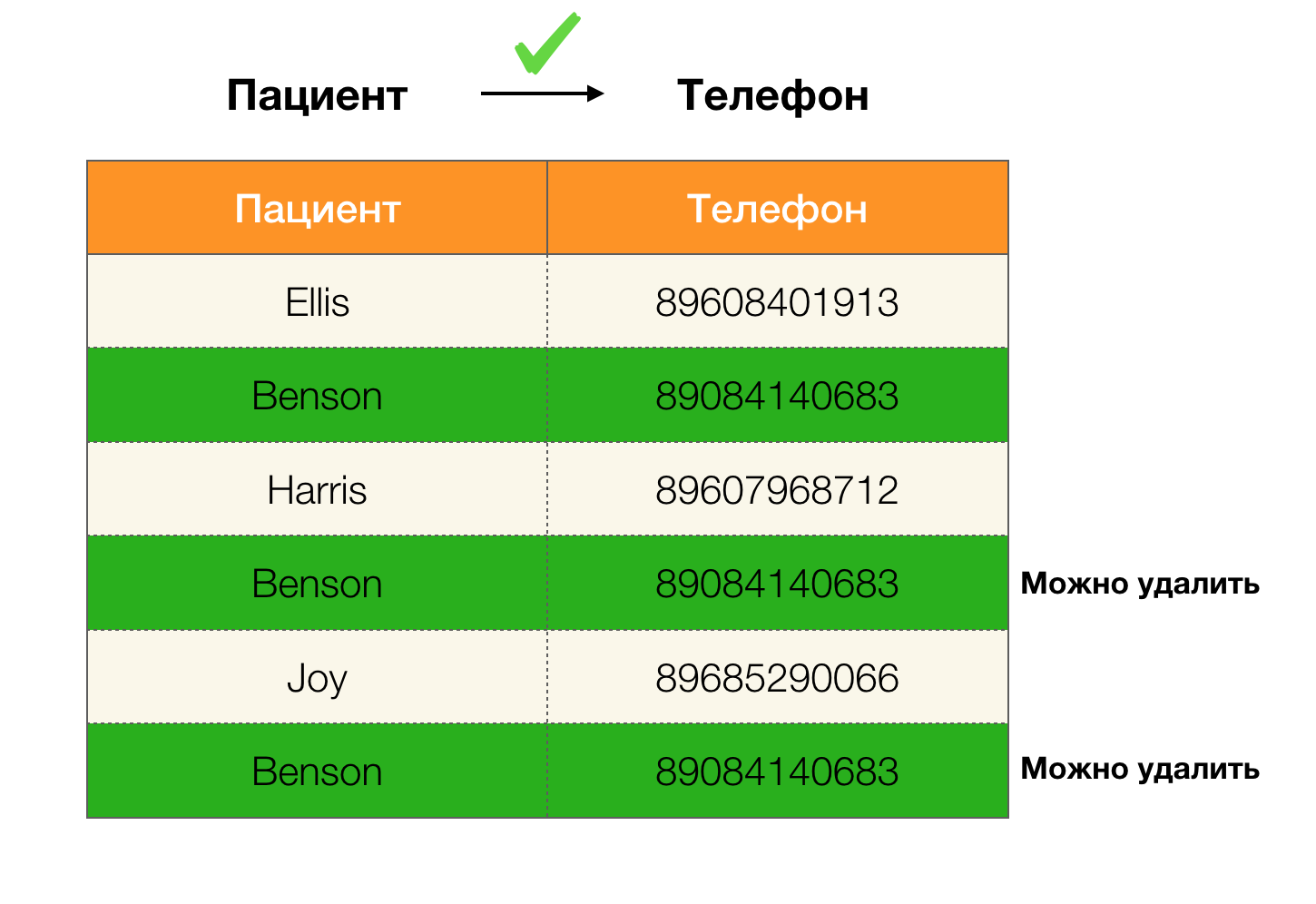
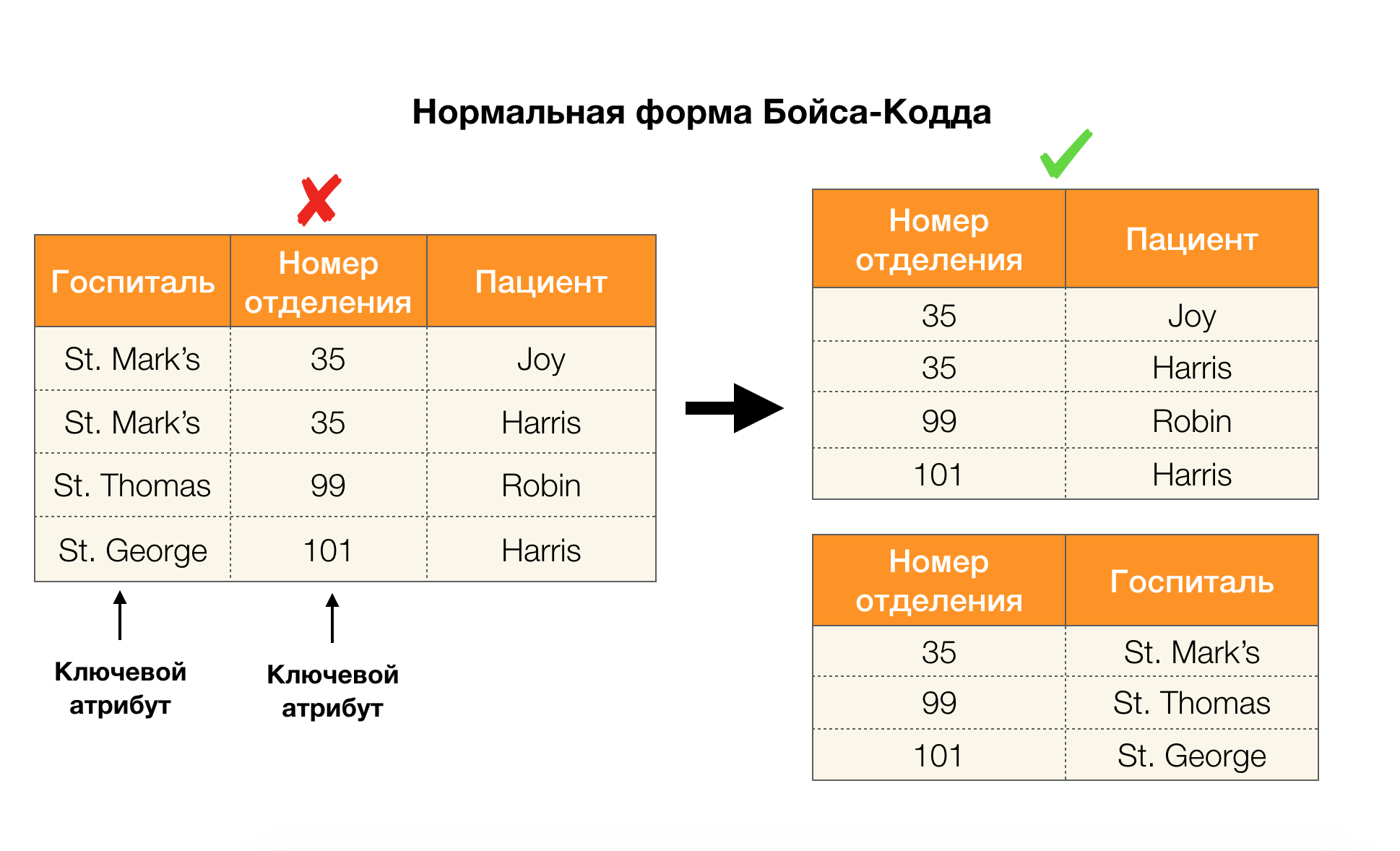
على سبيل المثال ، لدينا جدول ومجموعة من القوانين الفيدرالية التي يجب تنفيذها. يتضمن تنظيف البيانات في هذه الحالة تغيير البيانات بحيث تكون القوانين الفيدرالية صحيحة. في الوقت نفسه ، يجب أن يكون عدد التعديلات في حده الأدنى (بالنسبة لهذا الإجراء ، هناك خوارزميات لن نركز عليها في هذه المقالة). فيما يلي مثال لتحويل البيانات هذا. على اليسار هي العلاقة الأولية ، التي من الواضح أن القوانين الفيدرالية اللازمة لا تُستوفى (يتم إبراز مثال على انتهاك أحد القوانين الفيدرالية باللون الأحمر). على اليمين توجد علاقة محدثة تعرض فيها الخلايا الخضراء القيم المتغيرة. بعد هذا الإجراء ، بدأت التبعيات اللازمة في الصمود.



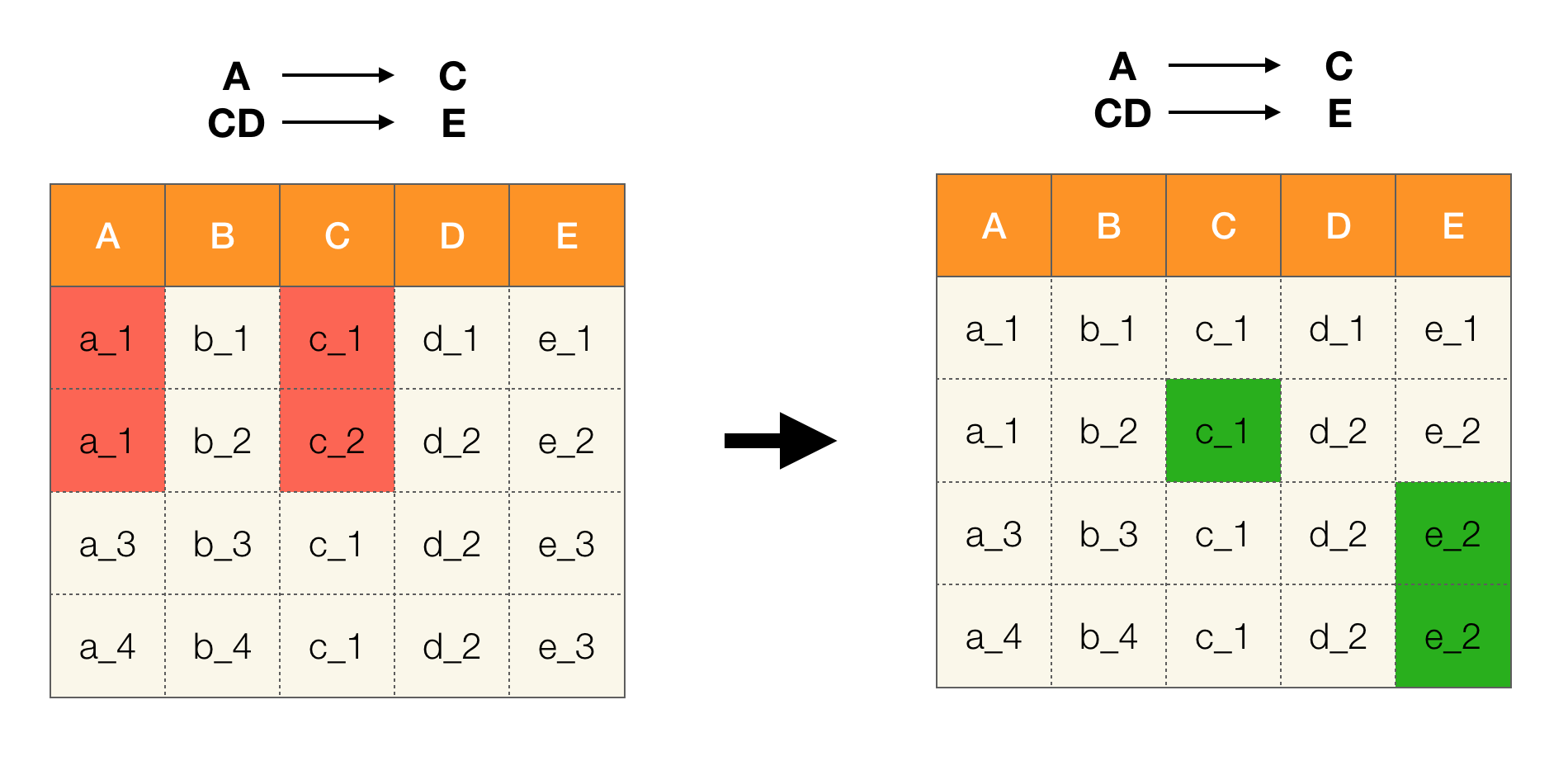
تطبيق شعبي آخر هو تصميم قاعدة البيانات. هنا تجدر الإشارة إلى الأشكال العادية والتطبيع. التطبيع هو عملية جعل العلاقة متماشية مع مجموعة معينة من المتطلبات ، يتم تحديد كل منها بطريقته الخاصة بواسطة شكل عادي. لن نقوم بتدوين متطلبات الأشكال العادية المختلفة (يتم ذلك في أي كتاب في دورة DB للمبتدئين) ، لكننا نلاحظ فقط أن كل واحد منهم يستخدم مفهوم التبعيات الوظيفية بطريقته الخاصة. في الواقع ، تعتبر القوانين الفيدرالية بطبيعتها قيودًا على النزاهة تؤخذ في الاعتبار عند تصميم قاعدة بيانات (في سياق هذه المهمة ، تسمى القوانين الفيدرالية أحيانًا بالمفاتيح الخارقة).

النظر في طلبهم للأشكال الأربعة العادية في الصورة أدناه. تذكر أن نموذج Boyce-Codd العادي أكثر صرامة من النموذج الثالث ، ولكنه أقل صرامة من النموذج الرابع. لا نعتبر هذا الأخير بعد ، لأن صياغته تتطلب فهم التبعيات متعددة القيم ، والتي لا تهمنا في هذه المقالة.






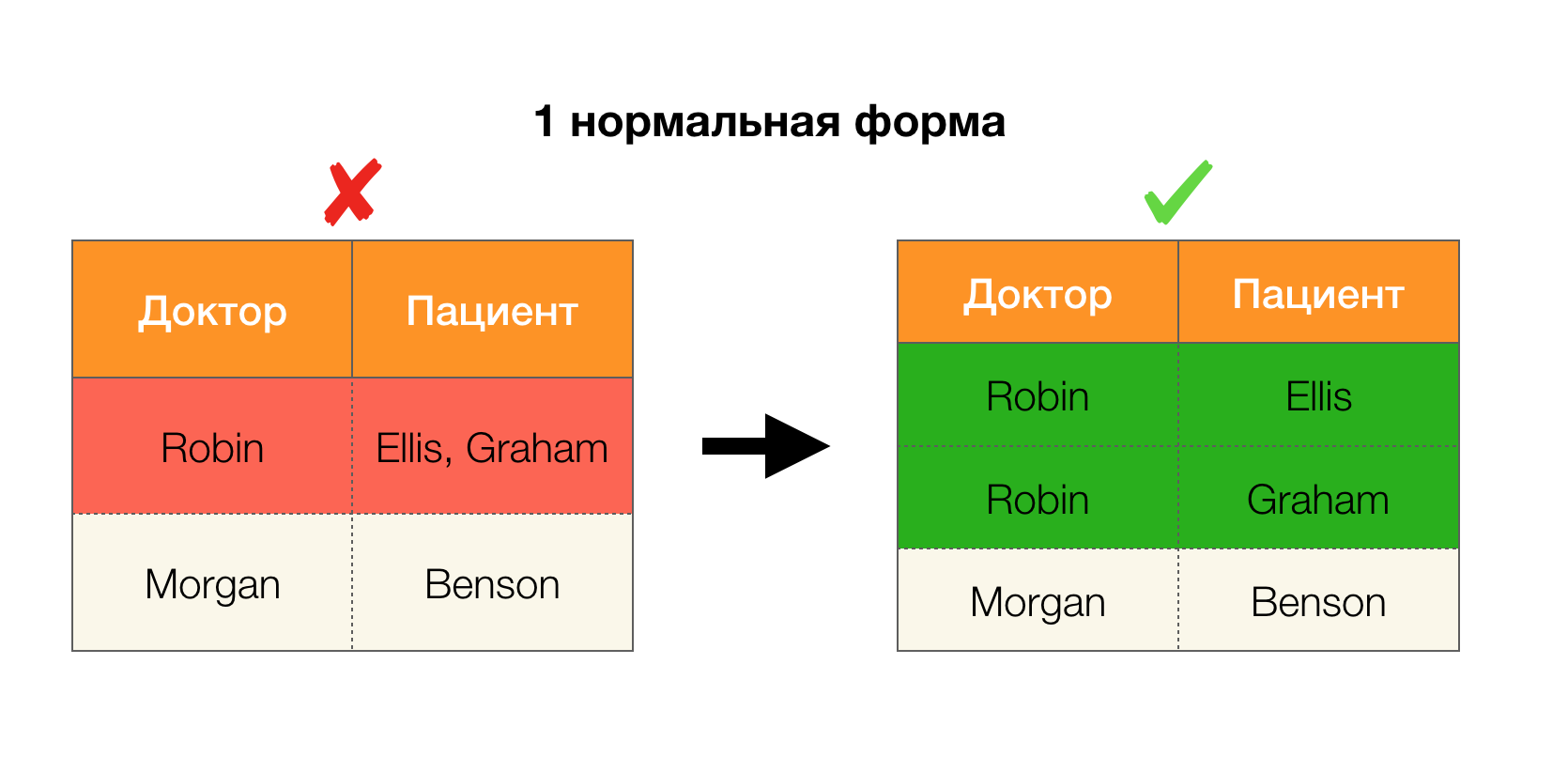
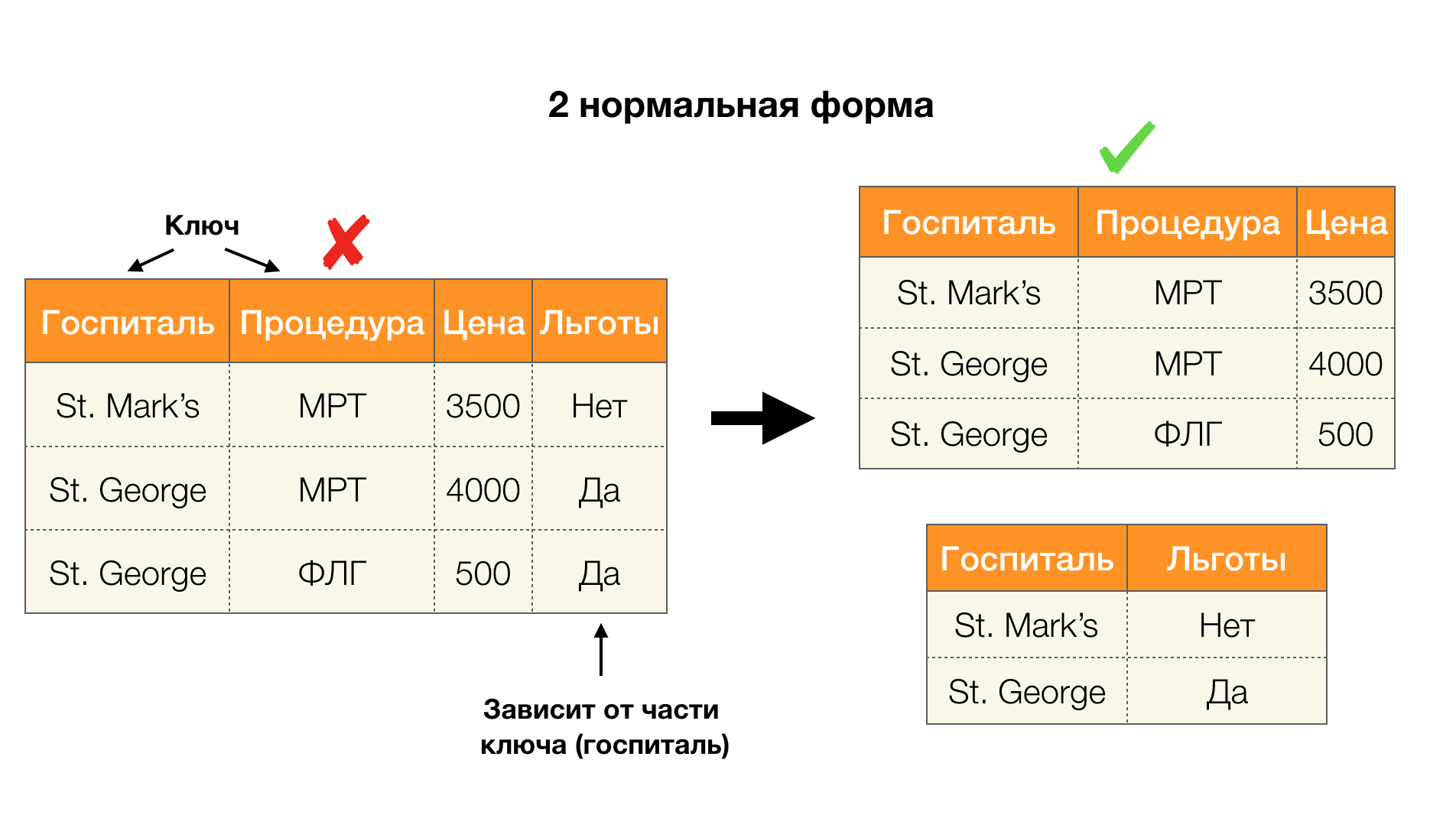
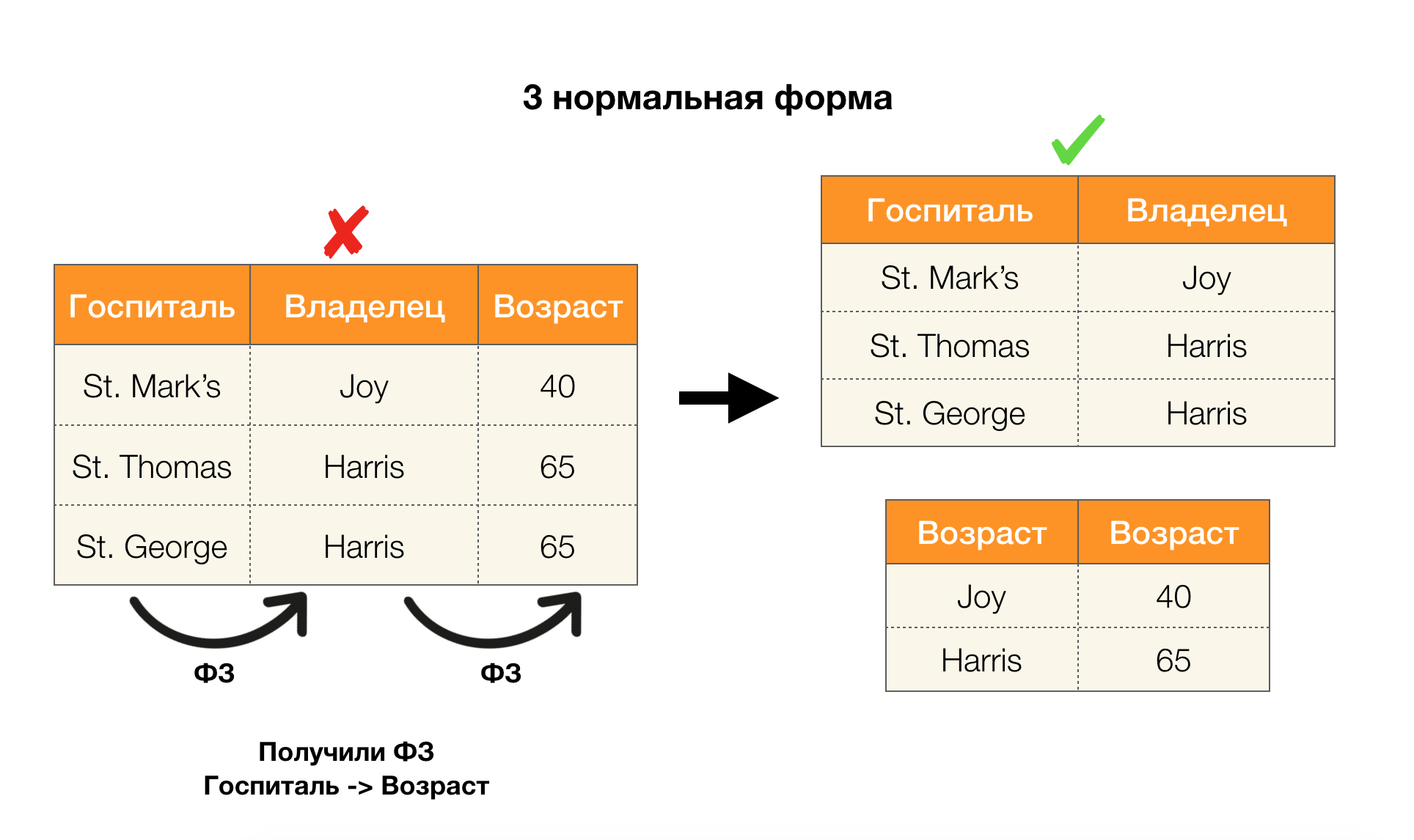
المجال الآخر الذي وجدت فيه التبعيات تطبيقها هو تقليل بُعد مساحة الميزة في مهام مثل إنشاء مصنف بايزي ساذج ، وتحديد الميزات المهمة ، وإعادة تجهيز نموذج الانحدار. في المقالات الأصلية ، تسمى هذه المشكلة تحديد الميزات المكررة ومدى ملاءمة الميزة [5 ، 6] ، ويتم حلها مع الاستخدام الفعال لمفاهيم قاعدة البيانات. مع ظهور مثل هذه الأعمال ، يمكننا القول أنه يوجد اليوم طلب للحلول التي تسمح بدمج قاعدة البيانات والتحليلات وتنفيذ مشاكل التحسين المذكورة أعلاه في أداة واحدة [7 ، 8 ، 9].

هناك العديد من الخوارزميات (الحديثة وغير الحديثة) للبحث عن القانون الفيدرالي في مجموعة بيانات ، ويمكن تقسيم هذه الخوارزميات إلى ثلاث مجموعات:

• الخوارزميات التي تستخدم اجتياز المشابك الجبرية (خوارزميات شعرية النقل)
• الخوارزميات المستندة إلى البحث عن قيم متسقة (الخوارزميات المحددة والتوافق)
• خوارزميات مقارنة الزوجية (خوارزميات تحريض التبعية)
  

يرد وصف موجز لكل نوع من الخوارزميات في الجدول أدناه:


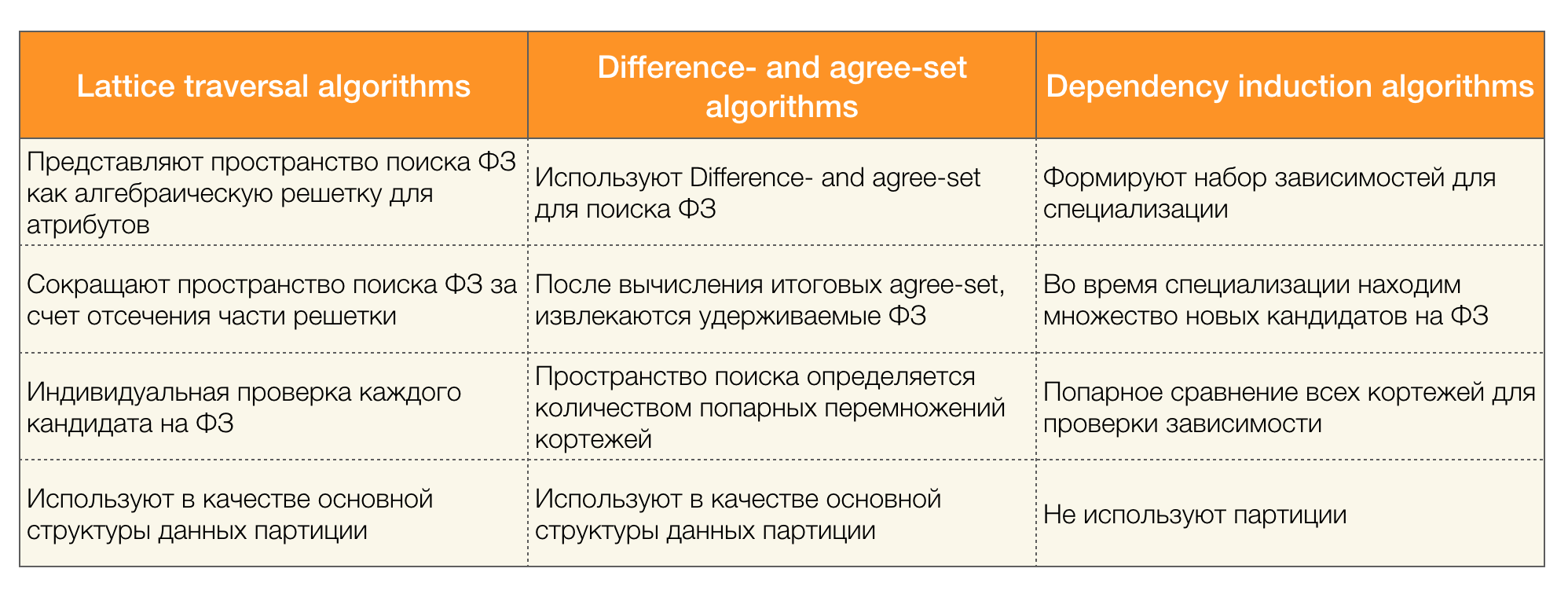
يمكن قراءة المزيد من التفاصيل حول هذا التصنيف [4]. فيما يلي أمثلة للخوارزميات لكل نوع:





حاليًا ، تظهر خوارزميات جديدة تجمع بين عدة طرق للبحث عن التبعيات الوظيفية دفعة واحدة. أمثلة هذه الخوارزميات هي Pyro [2] و HyFD [3]. تحليل عملهم متوقع في المقالات التالية من هذه السلسلة. في هذه المقالة ، سنقوم فقط بتحليل المفاهيم الأساسية و lemma الضرورية لفهم تقنيات اكتشاف التبعيات.

لنبدأ بمجموعة واحدة بسيطة ومختلفة ، تُستخدم في النوع الثاني من الخوارزميات. مجموعة التباينات هي مجموعة من المجموعات التي لا تتطابق مع القيم ، والمجموعة المتفق عليها ، على العكس ، هي المجموعات التي تتطابق في القيمة. تجدر الإشارة إلى أننا في هذه الحالة نعتبر فقط الجانب الأيسر من التبعية.

أيضا أحد المفاهيم المهمة التي تم استيفائها أعلاه هو الشبكة الجبرية. نظرًا لأن العديد من الخوارزميات الحديثة تعمل وفقًا لهذا المفهوم ، فنحن بحاجة إلى أن تكون لدينا فكرة عما هو عليه.

من أجل تقديم مفهوم الشبكة ، من الضروري تحديد مجموعة مرتبة جزئيًا (أو مجموعة مرتبة جزئيًا ، للإشارة القصيرة).

التعريف 2. يقال إن المجموعة S يتم طلبها جزئيًا بواسطة العلاقة الثنائية ⩽ إذا كانت الخصائص التالية مستوفاة لأي من أ ، ب ، ج:

1. الانعكاسية ، أي أ
2. عدم التماثل ، أي إذا كانت a ⩽ b و b ⩽ a ، ثم a = b
3. الانتقائية ، أي بالنسبة إلى a b و b ⩽ c ، يتبع ذلك a ⩽ c
   

تسمى هذه العلاقة بعلاقة بالترتيب الجزئي (غير الصارم) ، والمجموعة نفسها تسمى مجموعة مرتبة جزئيًا. التدوين الرسمي: ⟨S ، ⩽⟩.

كأبسط مثال على مجموعة مرتبة جزئيًا ، يمكننا أن نأخذ مجموعة من جميع الأرقام الطبيعية N مع العلاقة المعتادة بالترتيب ⩽. من السهل التحقق من أن جميع البديهيات اللازمة راضية.

مثال أكثر وضوحا. النظر في مجموعة من جميع المجموعات الفرعية {1 ، 2 ، 3} مرتبة حسب علاقة التضمين ⊆. في الواقع ، هذه العلاقة تلبي جميع شروط الترتيب الجزئي ؛ لذلك ، ⟨P ({1 ، 2 ، 3}) ، ⊆⟩ هي مجموعة مرتبة جزئيًا. يوضح الشكل أدناه بنية هذه المجموعة: إذا كان من عنصر ما يمكنك المشي على طول الأسهم إلى عنصر آخر ، فعندها تكون مرتبطة بالترتيب.



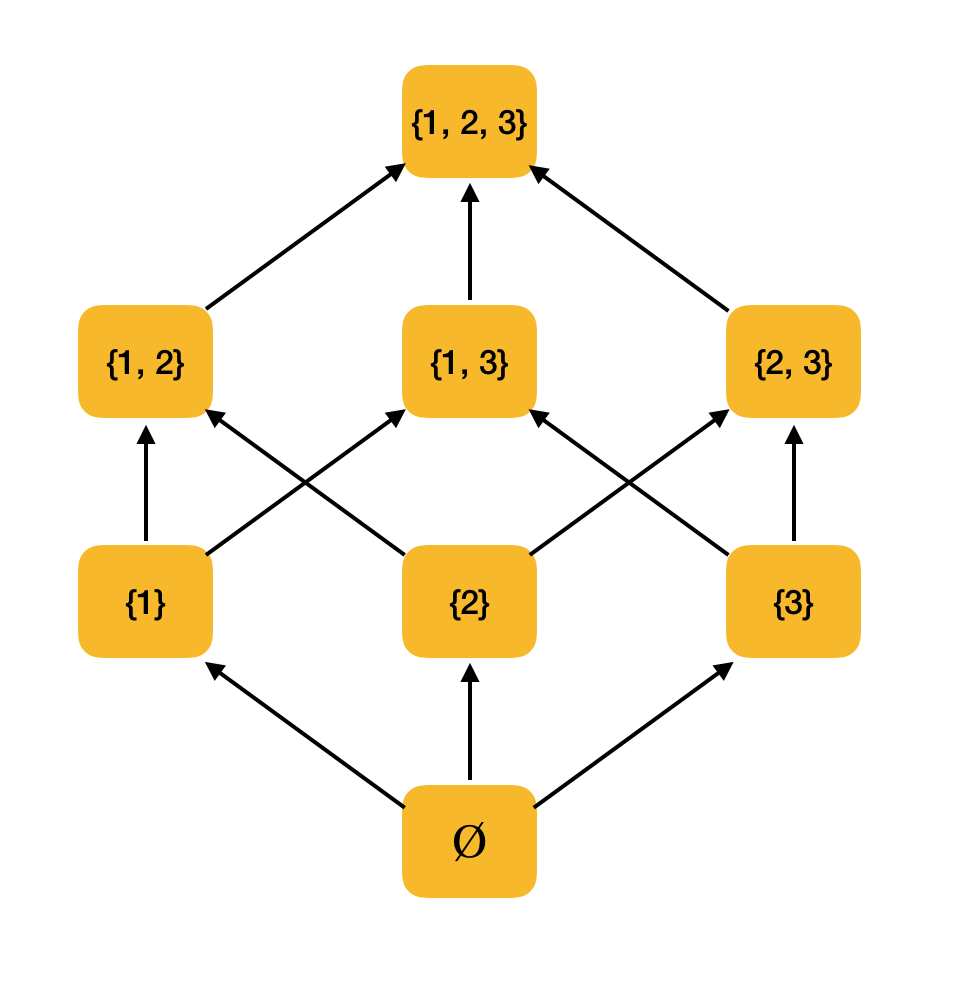
سنحتاج إلى تعريفين أكثر بساطة من مجال الرياضيات - التفوق والعدد.

التعريف 3. دع ⟨S ، ⩽⟩ عبارة عن مجموعة مرتبة جزئيًا ، A ⊆ S. الحدود العليا لـ A هي عنصر u such S بحيث ∀x ∈ A: x ⩽ u. اجعل U عبارة عن مجموعة من الحدود العليا لـ A. إذا كان U يحتوي على أصغر عنصر ، فسيطلق عليه اسم supremum ويُشار إليه بالرمز sup A.

وبالمثل ، يتم تقديم مفهوم الحد الأدنى الدقيق.

التعريف 4. دع ⟨S ، ⩽⟩ تكون مجموعة مرتبة جزئيًا ، A ⊆ S. الحدود الدنيا لـ A هي عنصر l ∈ S بحيث suchx ∈ A: l ⩽ x. اجعل L هو مجموعة كل الحدود السفلية لـ A. إذا كان L يحتوي على أكبر عنصر ، فسيُطلق عليه اسم infimum ويشار إليه بـ inf A.

خذ بعين الاعتبار ، على سبيل المثال ، ما ورد أعلاه تم تعيينه جزئياً ⟨P ({1 ، 2 ، 3}) ، يمكنك العثور على العلوية والعدد الأدنى فيه:



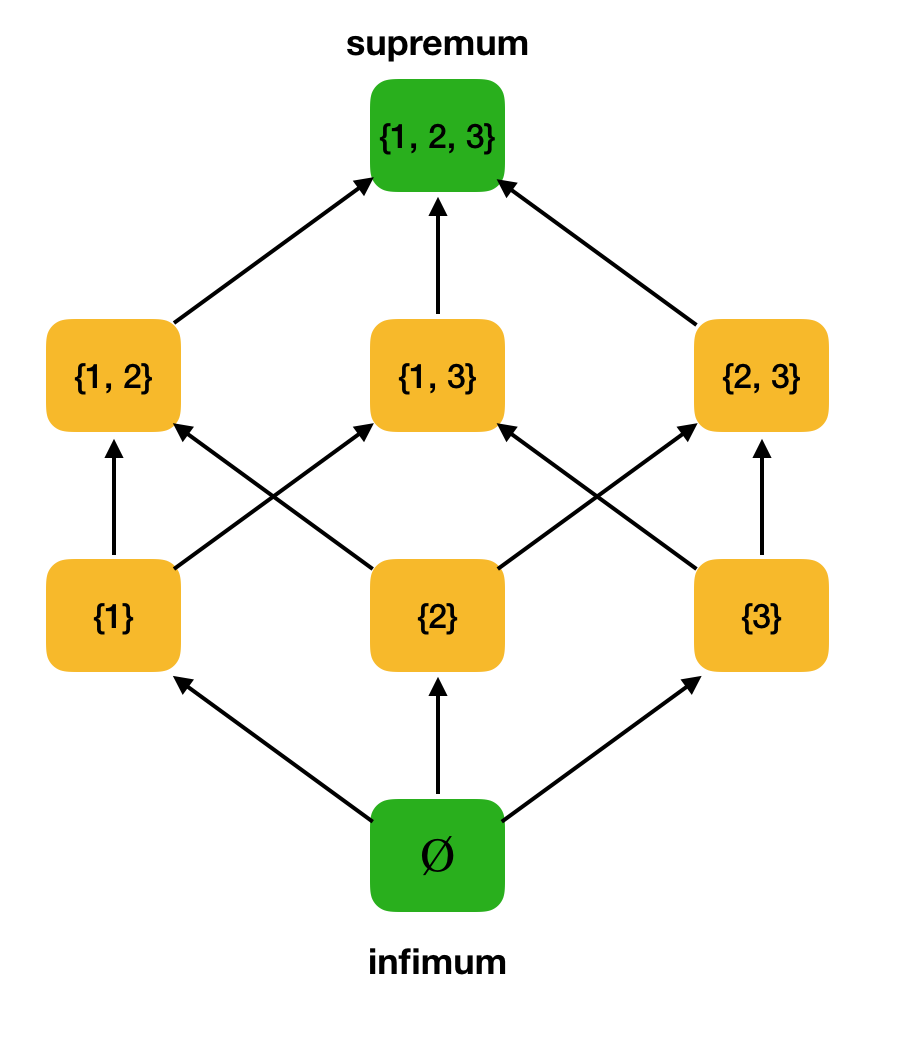
الآن يمكننا صياغة تعريف شعرية جبري.

التعريف 5. دع ⟨P ، ⩽⟩ عبارة عن مجموعة مرتبة جزئيًا بحيث تحتوي كل مجموعة فرعية من عنصرين على حدود علوية وسفلية محددة. ثم يسمى P شعرية جبري. علاوة على ذلك ، يتم كتابة sup {x، y} كـ x ∨ y ، و inf {x، y} - كـ x ∧ y.

نتحقق من أن مثالنا العامل ⟨P ({1 ، 2 ، 3}) ، ⊆⟩ هو شعرية. في الواقع ، بالنسبة لأي a ، b ∈ P ({1 ، 2 ، 3}) ، a∨b = a∪b ، و a∧b = a∩b. على سبيل المثال ، ضع في اعتبارك المجموعات {1 ، 2} و {1 ، 3} وابحث عن الحد الأدنى وتفوقها. إذا عبرناهم ، فسنحصل على المجموعة {1} ، والتي ستكون الحد الأدنى. نحصل على تفوق اتحادهم - {1 ، 2 ، 3}.

في خوارزميات اكتشاف FD ، يتم تمثيل مساحة البحث غالبًا في شكل شعرية ، حيث تكون مجموعات عنصر واحد (اقرأ المستوى الأول من شبكة البحث ، حيث يتكون الجزء الأيسر من التبعيات من سمة واحدة) هي كل سمة من سمات العلاقة الأصلية.
في البداية ، يتم النظر في تبعيات النموذج ∅ → سمة واحدة. تتيح لك هذه الخطوة تحديد السمات المميزة للمفاتيح الأساسية (لا توجد محددات لهذه السمات ، وبالتالي فإن الجانب الأيسر فارغ). علاوة على ذلك ، فإن هذه الخوارزميات ترفع الشبكة. تجدر الإشارة إلى أنه لا يمكن تجاوز الشبكة بأكملها ، أي إذا تم نقل الحد الأقصى للحجم المرغوب للجزء الأيسر إلى الإدخال ، فلن تتجاوز الخوارزمية المستوى مع هذا الحجم.

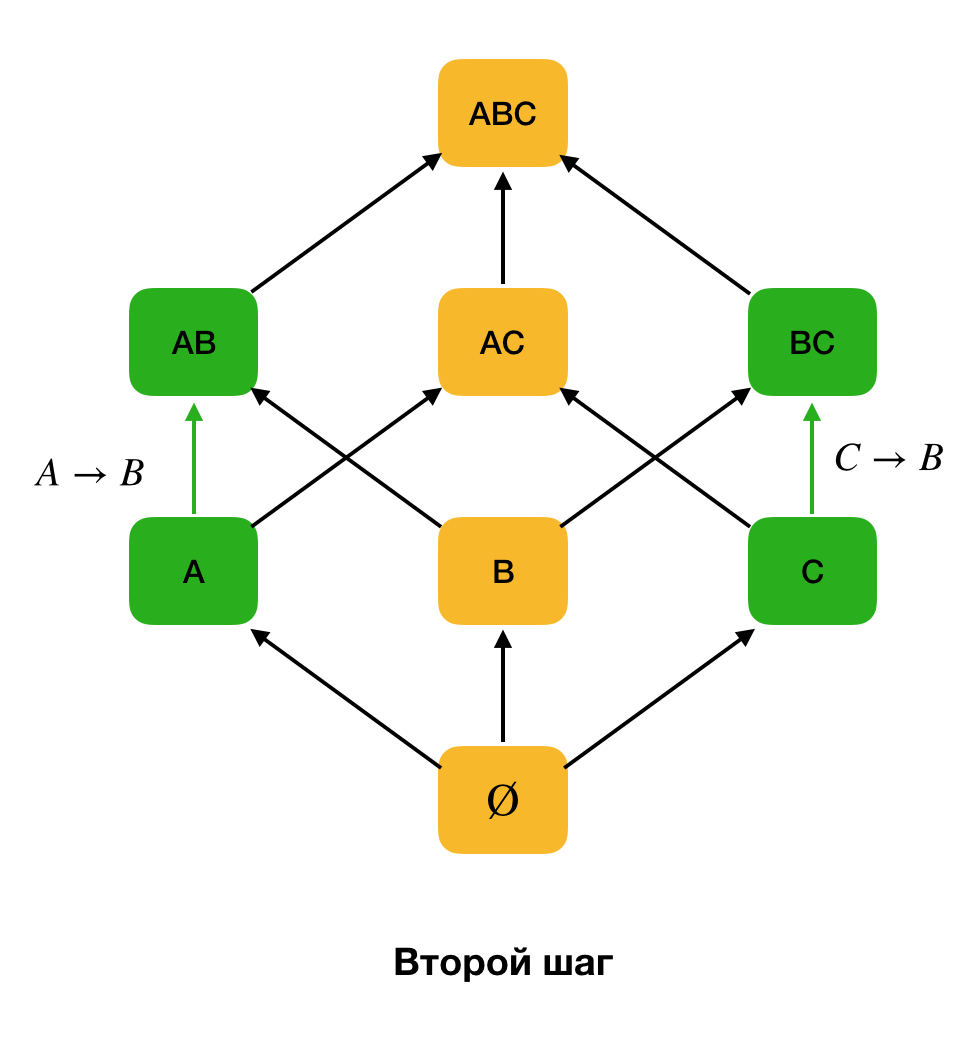
يوضح الشكل أدناه كيف يمكنك استخدام الشبكة الجبرية في مشكلة البحث عن القانون الفيدرالي. هنا ، تمثل كل حافة ( X ، XY ) تبعية X → Y. على سبيل المثال ، مررنا بالمستوى الأول ونعلم أنه يتم الاحتفاظ بالاعتماد A → B (سوف نعرض ذلك بالاتصال الأخضر بين القمم A و B ). لذلك ، عندما ننتقل إلى أعلى شعرية ، لا يمكننا التحقق من الاعتماد A ، C → B ، لأنه لن يكون الحد الأدنى. وبالمثل ، لن نختبره إذا تم الاحتفاظ بالاعتماد C → B.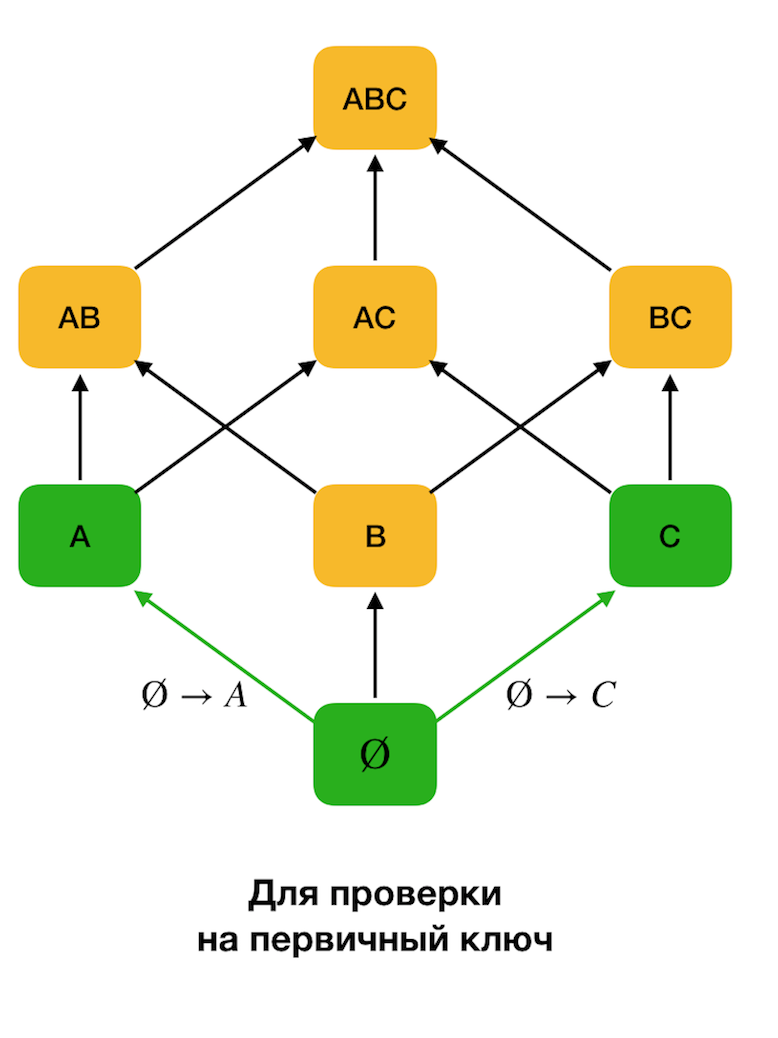




بالإضافة إلى ذلك ، وكقاعدة عامة ، تستخدم جميع خوارزميات البحث FZ الحديثة مثل بنية البيانات كقسم (قسم تم تجريده [1] في المصدر الأصلي). التعريف الرسمي للقسم هو كما يلي:

التعريف 6. اجعل X ⊆ R مجموعة من سمات العلاقة r. الكتلة هي مجموعة من مؤشرات tuples من r والتي لها نفس القيمة لـ X ، أي c (t) = {i | ti [X] = t [X]}. التقسيم هو مجموعة من المجموعات ، باستثناء مجموعات من طول الوحدة:

$$

$$\ pi (X): = \ {c (t) | t \ in r \ wedge | c (t) | > 1 \}$$

بعبارة بسيطة ، قسم السمة X هو مجموعة من القوائم ، حيث تحتوي كل قائمة على أرقام أسطر لها نفس قيم X. في الأدب الحديث ، يسمى الهيكل الذي يمثل الأقسام بفهرس قائمة المواقع (PLI). يتم استبعاد مجموعات طول الوحدة لضغط PLI لأنها مجموعات تحتوي فقط على رقم سجل بقيمة فريدة يسهل ضبطها دائمًا.

النظر في مثال. دعنا نعود إلى نفس الجدول مع المرضى ونبني أقسامًا لأعمدة " المريض" و " بول" (ظهر عمود جديد على اليسار ، مع تمييز أرقام صفوف الجدول):





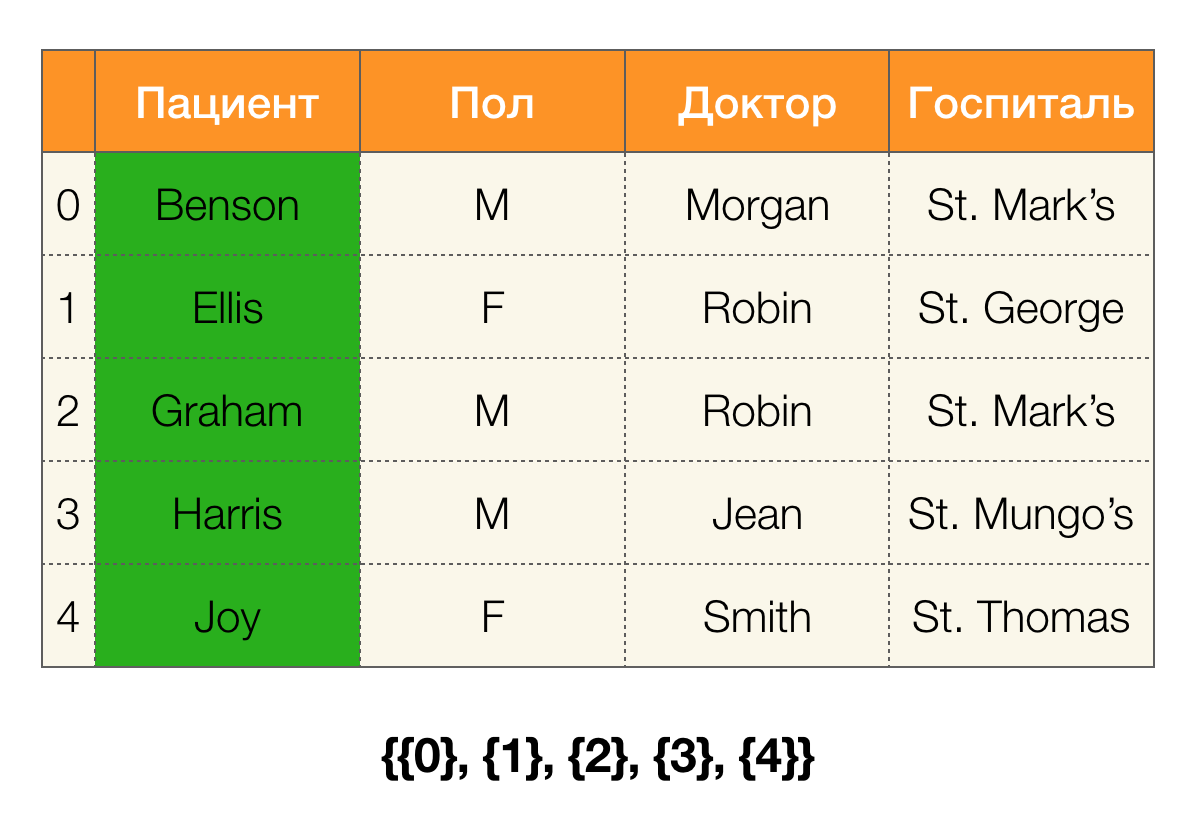
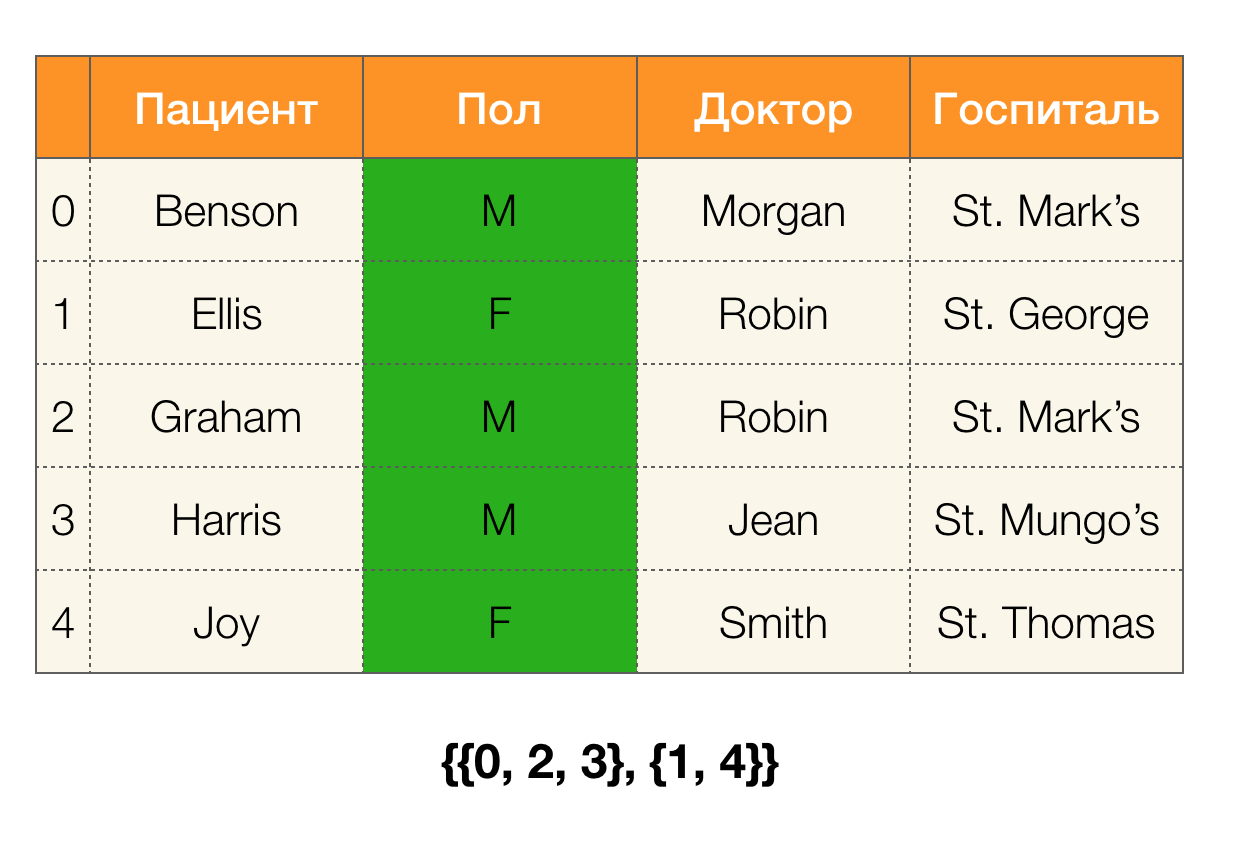
علاوة على ذلك ، وفقًا للتعريف ، سيكون القسم الخاص بعمود " المريض " فارغًا بالفعل ، نظرًا لاستبعاد المجموعات الفردية من القسم.

يمكن الحصول على أقسام بواسطة العديد من السمات. ولهذا هناك طريقتان: الانتقال إلى الجدول ، إنشاء قسم في وقت واحد وفقًا لكل السمات الضرورية ، أو إنشاءه باستخدام تشغيل الأجزاء المتقاطعة بواسطة مجموعة فرعية من السمات. تستخدم خوارزميات البحث FZ الخيار الثاني.

بعبارة بسيطة ، على سبيل المثال ، للحصول على قسم حسب أعمدة ABC ، يمكنك أن تأخذ أقسامًا لـ AC و B (أو أي مجموعة أخرى من مجموعات فرعية منفصلة) وتتقاطع مع بعضها البعض. تحدد عملية تقاطع قسمين مجموعات من أكبر طول مشترك لكلا القسمين.

لنلقِ نظرة على مثال:





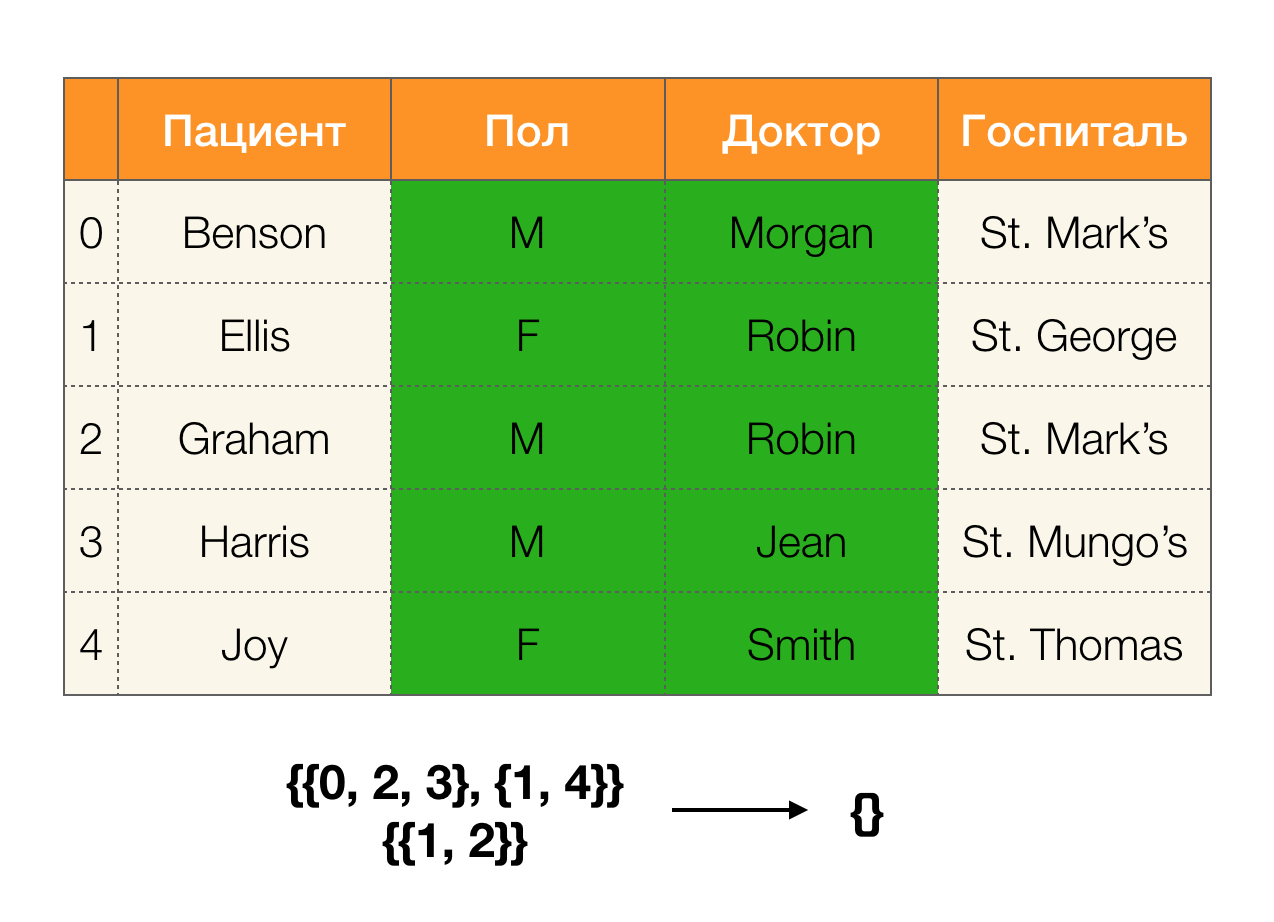
في الحالة الأولى ، تلقينا قسمًا فارغًا. إذا نظرت عن كثب إلى الجدول ، فحينئذٍ لا توجد القيم المتطابقة للسمتين. إذا قمنا بتعديل الجدول قليلاً (الحالة على اليمين) ، فسنحصل بالفعل على تقاطع غير فارغ. في الوقت نفسه ، يحتوي السطران 1 و 2 حقًا على نفس القيم لسمات Paul and Doctor .

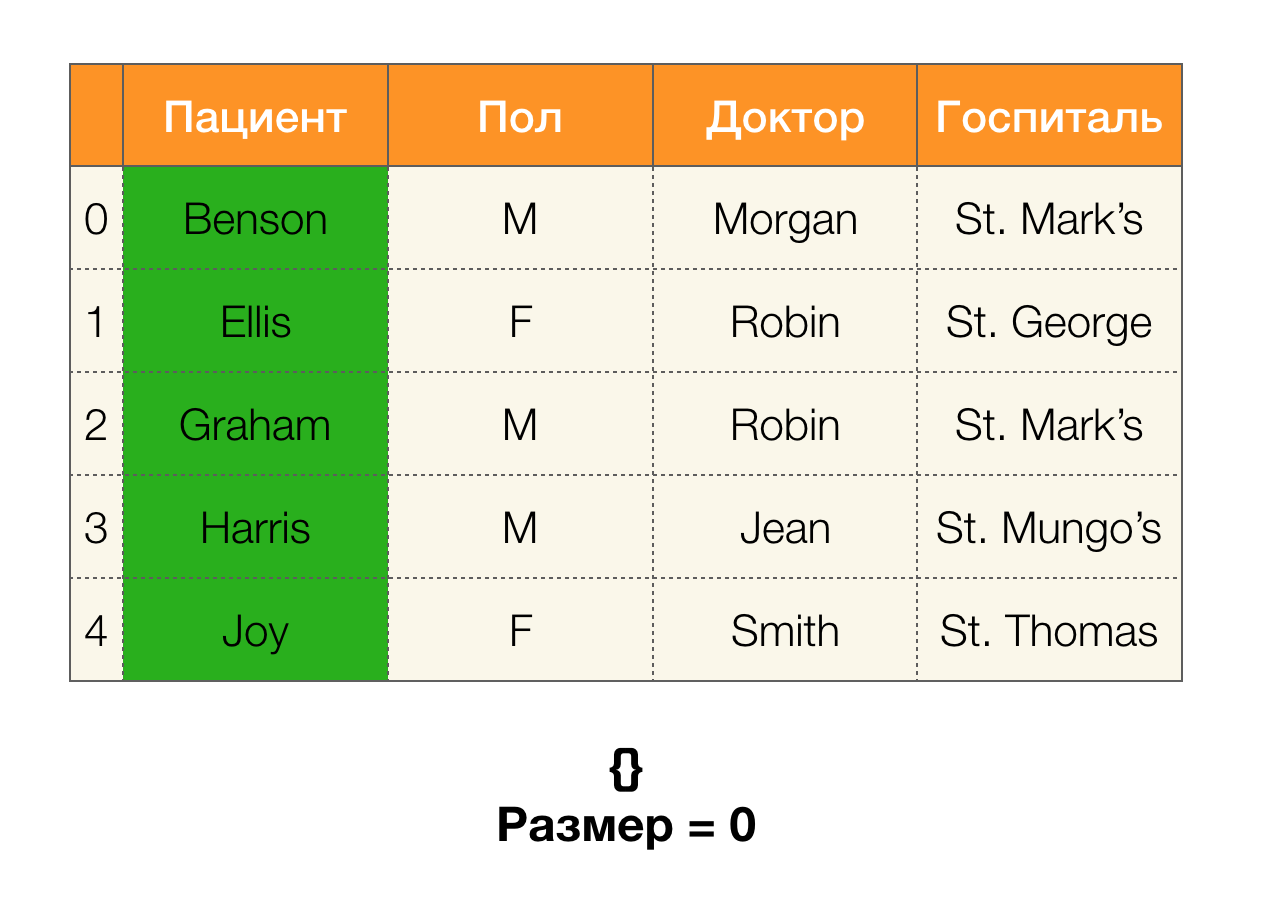
بعد ذلك ، نحتاج إلى مفهوم مثل حجم القسم. رسميا:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

ببساطة ، حجم القسم هو عدد الكتل المضمنة في القسم (تذكر أن الكتل الفردية غير مدرجة في القسم!):





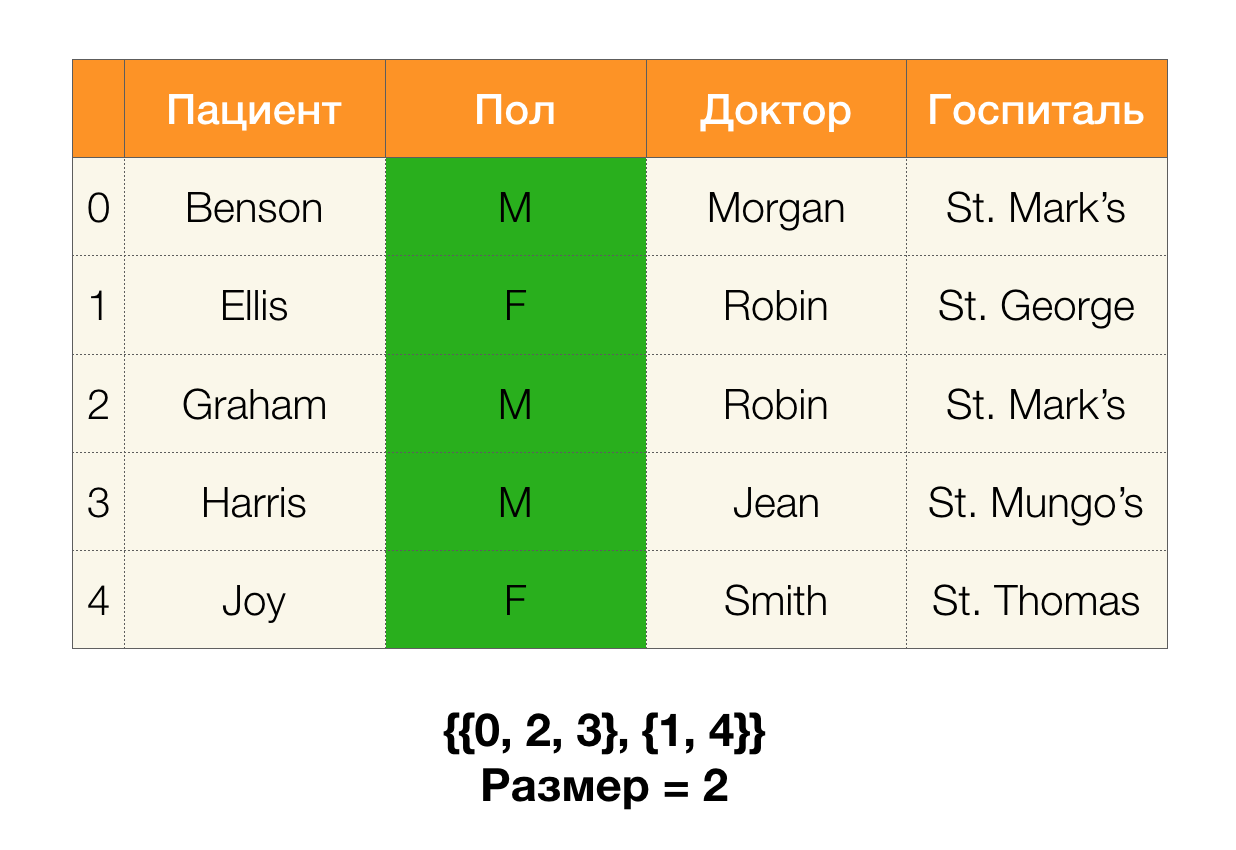
يمكننا الآن تحديد واحد من lemmas الرئيسي ، والذي يسمح لنا في أقسام معينة بتحديد ما إذا كانت التبعية أم لا:

ليما 1 . يتم الاعتماد على A و B → C إذا وفقط إذا

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

وفقًا لـ lemma ، لتحديد ما إذا كانت هناك تبعية أم لا ، يجب تنفيذ أربع خطوات:

1. حساب القسم للجانب الأيسر من التبعية
2. حساب القسم على الجانب الأيمن من التبعية
3. حساب المنتج من الخطوات الأولى والثانية
   
4. قارن أحجام الأقسام التي تم الحصول عليها في الخطوة الأولى والثالثة
   

فيما يلي مثال على التحقق مما إذا كان الاعتماد يتم صيانته بواسطة هذا اللما:






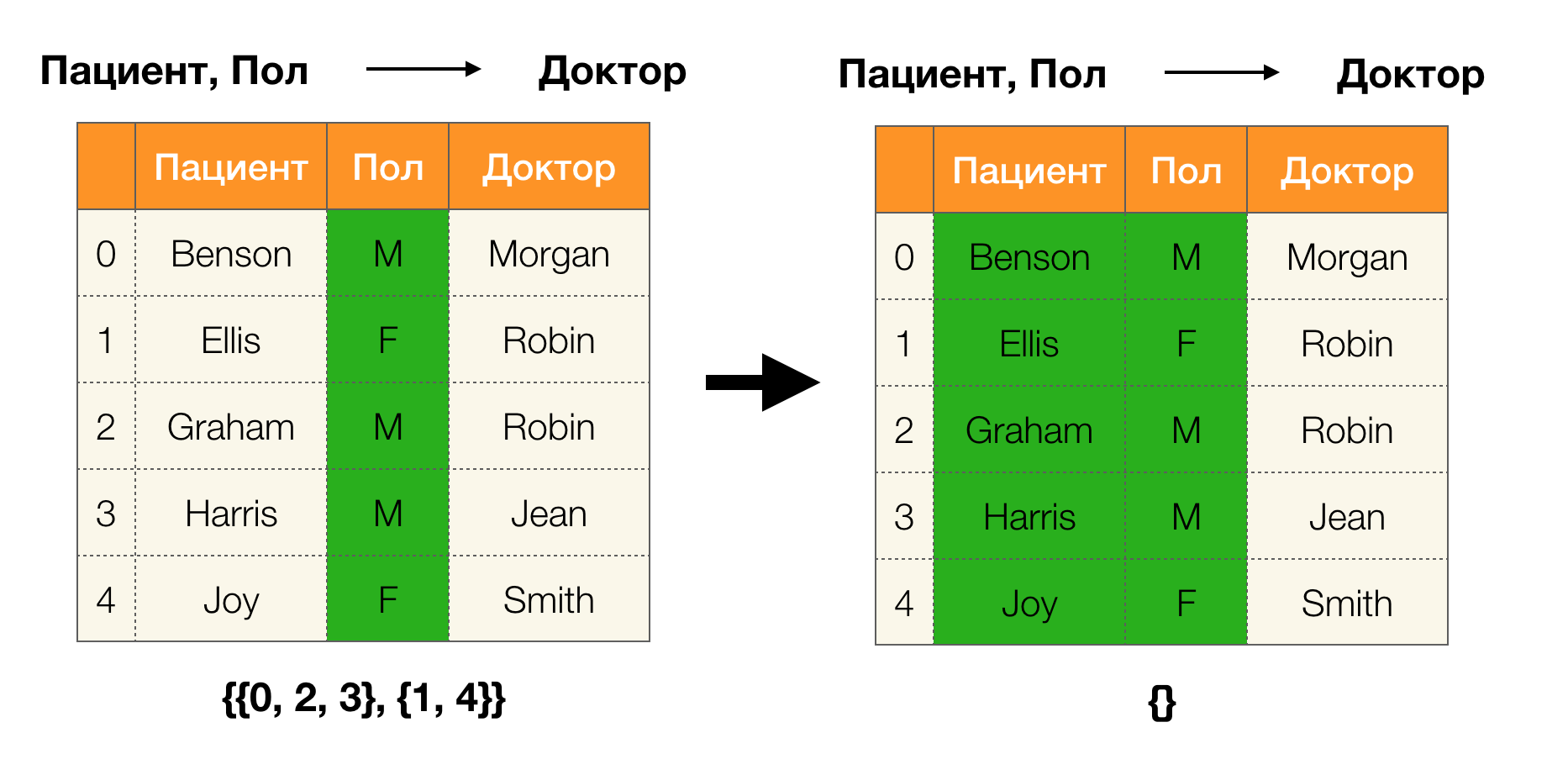
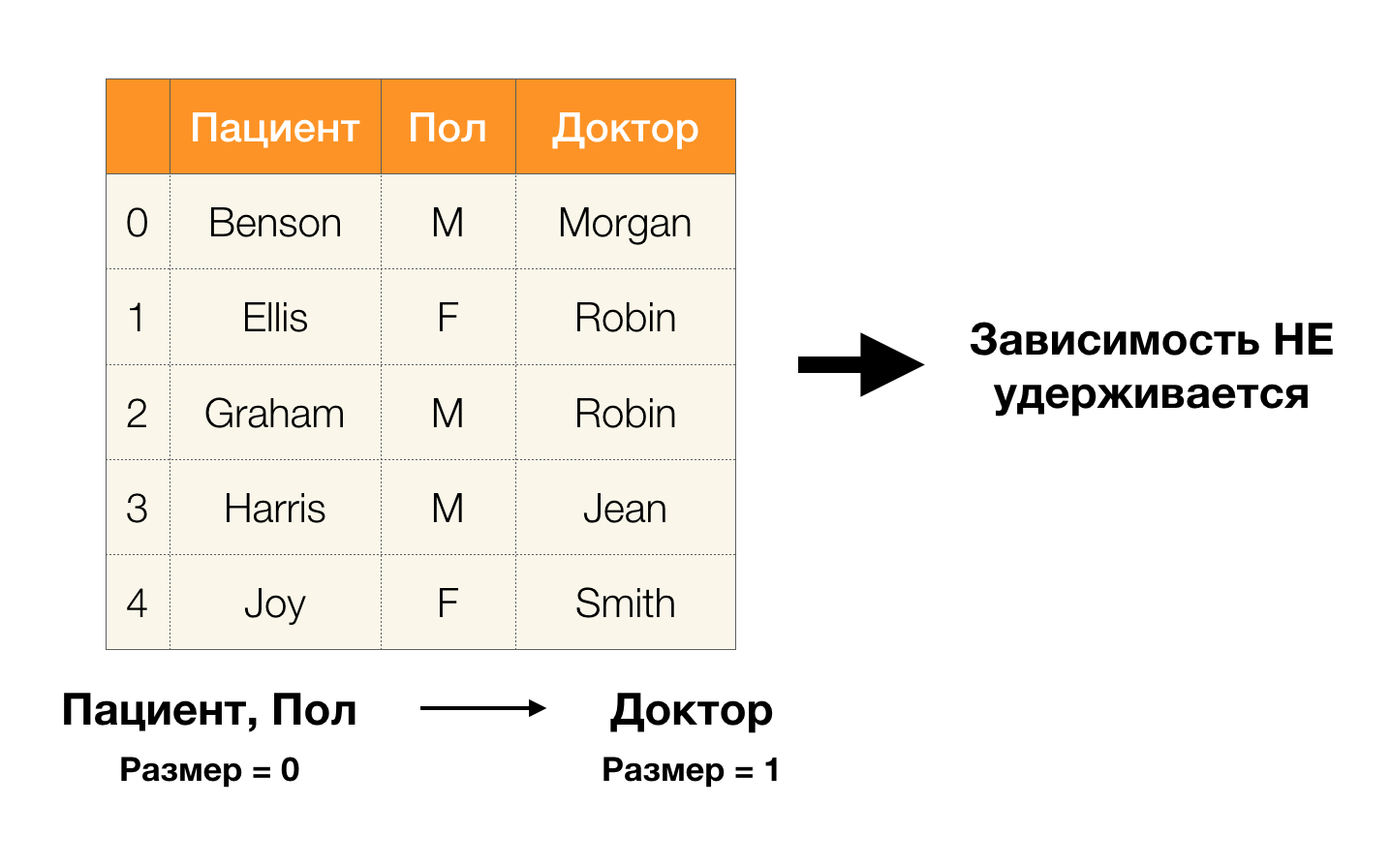
في هذه المقالة ، درسنا مفاهيم مثل التبعية الوظيفية ، التبعية الوظيفية التقريبية ، التي تم فحصها حيث يتم استخدامها ، وكذلك خوارزميات البحث عن القانون الاتحادي الموجودة. لقد درسنا أيضًا بالتفصيل المفاهيم الأساسية ، ولكن المهمة التي يتم استخدامها بنشاط في الخوارزميات الحديثة للبحث عن القوانين الفيدرالية.

مراجع إلى الأدب:

1. هوستالا ي. وآخرون. تان: خوارزمية فعالة لاكتشاف التبعيات الوظيفية والتقريبية // مجلة الكمبيوتر. - 1999. - T. 42. - رقم 2. - س 100-111.
2. Kruse S.، Naumann F. اكتشاف فعال للتبعيات التقريبية // وقائع VLDB الوقف. - 2018. - T. 11. - رقم 7 - س 759-772.
3. Papenbrock T. ، Naumann F. نهج هجين لاكتشاف التبعية الوظيفية // وقائع المؤتمر الدولي لعام 2016 بشأن إدارة البيانات. - ACM ، 2016. - S. 821-833.
4. Papenbrock T. et al. اكتشاف التبعية الوظيفية: تقييم تجريبي لسبع خوارزميات // وقائع VLDB الوقف. - 2015. - T. 8. - رقم 10. - س 1082-1093.
5. كومار إيه وآخرون. للانضمام أو عدم الانضمام؟: التفكير مرتين في الصلات قبل اختيار الميزة // وقائع المؤتمر الدولي 2016 لإدارة البيانات. - ACM ، 2016. - S. 19-34.
6. أبو خميس محمد وآخرون. التعلم داخل قاعدة البيانات باستخدام التنسورات المتناثرة // وقائع الندوة السابعة والثلاثين لـ ACM SIGMOD-SIGACT-SIGAI حول مبادئ أنظمة قواعد البيانات. - ACM ، 2018. - S. 325-340.
7. هيلرستين جي إم وآخرون. مكتبة تحليلات MADlib: أو مهارات MAD ، SQL // Proceedings of VLDB Endowment. - 2012. - T. 5. - رقم 12. - س 1700-1711.
8. Qin C.، Rusu F. التقريب المضاربي لتحصيل النسب المتدرج الموزع terascale // وقائع ورشة العمل الرابعة حول تحليلات البيانات في السحابة. - ACM ، 2015. - S. 1.
9. منغ اكس وآخرون. مليب: تعلم الآلة في شرارة أباتشي // مجلة أبحاث التعلم الآلي. - 2016. - T. 17. - رقم 1-س 1235-1241.

مؤلفو المقال: أنستازيا بيريلو ، باحثة في JetBrains Research ، وطالبة في مركز CS ، ونيكيتا بوبروف ، باحثة في JetBrains Research