تحليل مفصل للطريقة البسيط

فاتحة

في الآونة الأخيرة ، كانت هناك حاجة لإنشاء برنامج من البداية يقوم بتنفيذ خوارزمية أسلوب simplex. لكن في سياق الحل ، واجهت مشكلة: لا توجد موارد كثيرة على الإنترنت حيث يمكنك الاطلاع على تحليل نظري مفصل للخوارزمية (الأساس المنطقي: لماذا نتخذ هذه الخطوات أو تلك الخطوات) ونصائح التنفيذ العملية - مباشرة ، الخوارزمية. ثم قدمت نفسي وعدًا - بمجرد إكمال المهمة ، سأكتب مشاركتي حول هذا الموضوع. في الواقع ، سنتحدث عن هذا.

المذكرة. سيتم كتابة المنشور بلغة رسمية إلى حد ما ، ولكن سيتم تزويده بتعليقات ، والتي ينبغي أن تجلب بعض الوضوح. سوف يحافظ هذا التنسيق على النهج العلمي ، وفي الوقت نفسه ، قد يساعد البعض في دراسة هذه المسألة.

§1. بيان مشكلة البرمجة الخطية

التعريف: البرمجة الخطية هي تخصص رياضي مكرس لنظرية وطرق حل المشكلات المتطرفة على مجموعات من الأبعاد ذات الأبعاد n المحددة بواسطة أنظمة المعادلات الخطية وعدم المساواة.

المهمة العامة للبرمجة الخطية (المشار إليها فيما يلي - LP) لها الشكل:

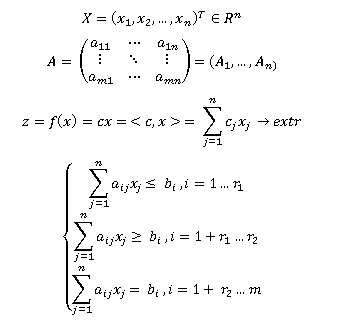
§2. الشكل المتعارف عليه لمشكلة LP

الشكل المتعارف عليه لمشكلة LP:



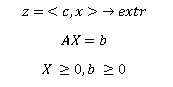ملاحظة: أي مشكلة LP يقلل إلى الكنسي.

الخوارزمية للانتقال من مشكلة LP التعسفية إلى النموذج الأساسي:

1. عدم المساواة مع سلبية$$ $ inline $ b_i $ inline $ اضرب ب (-1).
2. إذا كان عدم المساواة في النموذج (≤) ، فقم بإضافة إلى الجانب الأيسر$$ $ inline $ s_i $ inline $ هو متغير إضافي ، ونحن نحصل على المساواة.
3. إذا كان عدم المساواة في النموذج (≥) ، ثم اطرح من الجانب الأيسر$$ $ inline $ s_i $ inline $ ، ونحن نحصل على المساواة.
4. نقوم باستبدال المتغيرات:

• إذا$$ $ inline $ x_i ≤ 0 $ inline $ ثم$$ $ inline $ x_i '= -x_i ≥ 0 $ inline $
• إذا$$ $ inline $ x_i $ inline $ - اي$$ $ inline $ x_i = x_i '- x_i' '$ inline $ حيث$$ $ inline $ x_i '، x_i''≥ 0 $ inline $

ملاحظة: سنقوم بالرقم$$ $ inline $ s_i $ inline $ بعدد عدم المساواة الذي أضفناه إليه.

ملاحظه:$$ $ inline $ s_i $ inline $ ≥0.

§3. نقاط الزاوية. المتغيرات الأساسية / الحرة. الحلول الأساسية

التعريف: نقطة$$ $ مضمنة $ X ∈ D $ مضمنة دعا نقطة الزاوية إذا كان التمثيل$$ $ inline $ X = αX ^ 1 + (1-α) X ^ 2 ، حيث X ^ 1 ، X ^ 2 ∈ D ؛ 0 <α <1 $ مضمّن $ ممكن فقط مع$$ $ inline $ X ^ 1 = X ^ 2 $ inline $ .

بمعنى آخر ، من المستحيل إيجاد نقطتين في المنطقة ، الفاصل الزمني الذي يحتوي على$$ $ مضمنة $ X $ مضمنة (أي$$ $ مضمنة $ X $ مضمنة ليست نقطة داخلية).

توضح الطريقة الرسومية لحل مشكلة LP أن إيجاد الحل الأمثل يرتبط بنقطة ركن. هذا هو المفهوم الأساسي عند تطوير أسلوب بسيط.

التعريف: دع نظام المعادلات m و n غير معروف (m <n). نقسم المتغيرات إلى مجموعتين: (نانومتر) نقوم بتعيين المتغيرات تساوي الصفر ، ويتم تحديد المتغيرات المتبقية م عن طريق حل نظام المعادلات الأولية. إذا كان هذا الحل فريدًا ، فسيتم استدعاء المتغيرات غير الصفرية الأساسية ؛ متغيرات الصفر (نانومتر) - خالية (غير أساسية) ، والقيم الناتجة المقابلة للمتغيرات تسمى الحل الأساسي.

§4. طريقة البسيط

تسمح لك طريقة simplex بالعثور على الحل الأمثل بفعالية ، وتجنب التعداد البسيط لجميع نقاط الزاوية الممكنة. المبدأ الأساسي للطريقة: تبدأ العمليات الحسابية بنوع من الحلول الأساسية "البدء" ، ثم يتم البحث عن حلول "تحسن" قيمة الوظيفة الموضوعية. هذا ممكن فقط إذا كانت الزيادة في بعض المتغيرات تؤدي إلى زيادة في قيمة الوظيفية.

المتطلبات الأساسية لتطبيق طريقة simplex:

1. يجب أن يكون للمهمة شكل قانوني.
2. يجب أن يكون للمهمة أساس واضح.

التعريف: الأساس المحدد صراحةً هو ناقل للنموذج:$$ $ inline $ (.. 0100 ..) ^ T ، (..010 ..) ^ T ، (.. 0010 ..) ^ T ... $ inline $ ، أي إحداثي واحد فقط من المتجه غير صفري ويساوي 1.

ملاحظة: المتجه الأساسي له بعد (m * 1) ، حيث m هو عدد المعادلات في نظام القيد.

لتسهيل العمليات الحسابية والتصور ، عادةً ما تستخدم الجداول البسيطة:

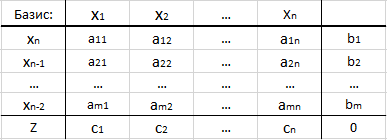
• يشير السطر الأول إلى "اسم" جميع المتغيرات.
• في العمود الأول ، تتم الإشارة إلى أرقام متغيرات الأساس ، وفي الحرف الأخير ، الحرف Z (هذا هو الخط الوظيفي).
• في "منتصف الجدول" تشير إلى معاملات مصفوفة القيد - aij.
• العمود الأخير هو متجه الجوانب اليمنى من المعادلات المقابلة لنظام القيد.
• الخلية الموجودة في أقصى اليمين هي قيمة الوظيفة الموضوعية. في التكرار الأول ، يفترض أن يكون 0.

ملاحظة: الأساس هو المتغيرات والمعاملات في مصفوفة القيود التي تشكل المتجهات الأساس.

ملاحظة: إذا كانت القيود في المشكلة الأصلية تتمثل في عدم المساواة في النموذج ≤ ، فعندما يتم تقليل المشكلة إلى شكل أساسي ، فإن المتغيرات الإضافية المقدمة تشكل الحل الأساسي الأولي.

ملاحظة: يتم أخذ المعاملات في الخط الوظيفي بعلامة "-".

خوارزمية أسلوب بسيط:

1. اختر المتغير الذي سنقدمه في الأساس. يتم ذلك وفقًا للمبدأ الموضح سابقًا: يجب علينا اختيار متغير ستؤدي زيادته إلى زيادة في الوظيفية. يتم الاختيار وفقًا للقاعدة التالية:

• إذا كانت المهمة على الأقل ، فحدد الحد الأقصى للعنصر الموجب في الصف الأخير.
• إذا كانت المهمة في الحد الأقصى ، فحدد الحد الأدنى السلبي.

مثل هذا الاختيار ، في الواقع ، يتوافق مع المبدأ المذكور أعلاه: إذا كانت المهمة في الحد الأدنى ، فكلما زاد العدد الذي نطرحه ، كلما انخفضت الوظيفة بشكل أسرع ؛ إلى الحد الأقصى ، على العكس - كلما زاد العدد ، زاد نمو الوظائف بشكل أسرع.

ملاحظة: على الرغم من أننا نأخذ الحد الأدنى للرقم السلبي في المشكلة إلى الحد الأقصى ، فإن هذا المعامل يوضح اتجاه نمو الوظيفية ، لأن يتم أخذ الخط الوظيفي في الجدول البسيط بعلامة "-". وضع مماثل مع التقليل.

التعريف: يسمى عمود جدول بسيط يتوافق مع معامل محدد عمود بادئة .

2. اختر المتغير الذي سنقدمه في الأساس. للقيام بذلك ، تحتاج إلى تحديد أي من المتغيرات الأساسية من المرجح أن تختفي عندما ينمو المتغير الأساسي الجديد. جبريًا ، يتم ذلك على النحو التالي:

• يتم تقسيم متجه الأجزاء اليمنى على عمود الإنهاء
• من بين القيم التي تم الحصول عليها اختيار الحد الأدنى الإيجابي (لا تؤخذ في الاعتبار الإجابات السلبية والصفرية)

التعريف: يسمى هذا الخط سطرًا أوليًا ويتوافق مع متغير يتم اشتقاقه من الأساس.

ملاحظة: في الواقع ، نعبر عن متغيرات الأساس القديمة من كل معادلة لنظام القيد إلى بقية المتغيرات ونرى في المعادلة التي من المرجح أن تعطيها زيادة المتغير الأساسي الجديد 0. الدخول في هذا الموقف يعني أننا "تعثرنا" في قمة جديدة. هذا هو السبب في عدم اعتبار العناصر صفر والسلبي ، لأنه الحصول على مثل هذه النتيجة يعني أن اختيار مثل هذا المتغير الأساسي الجديد سيقودنا بعيدًا عن المنطقة التي لا توجد بعدها حلول.

3. نحن نبحث عن عنصر يقف عند تقاطع الصف والعمود.

التعريف: مثل هذا العنصر يسمى العنصر الرئيسي .

4. بدلاً من المتغير الذي سيتم استبعاده ، في العمود الأول (مع أسماء المتغيرات الأساسية) ، اكتب اسم المتغير الذي ندخله في الأساس.

5. بعد ذلك ، تبدأ عملية حساب حل أساسي جديد. يحدث ذلك باستخدام طريقة Jordan-Gauss .

• خط الرصاص الجديد = خط الرصاص القديم / الرصاص
• صف جديد = صف جديد - عامل صف في العمود بادئة * صف بادئة جديد

ملاحظة: يهدف هذا النوع من التحويل إلى إدخال المتغير المحدد في الأساس ، أي تمثيل العمود البادئة كمتجه أساسي.

6. بعد ذلك ، نتحقق من حالة الأمثلية. إذا لم يكن الحل الناتج هو الأمثل ، كرر العملية بأكملها مرة أخرى.

§5. تفسير نتيجة طريقة simplex

1. الأمثلية

شرط الأمثلية للحل الناتج:

• إذا كانت المهمة في الحد الأقصى ، فلا توجد معاملات سلبية في الصف الوظيفي (أي مع أي تغيير في المتغيرات ، لن تنمو قيمة الوظيفة الناتجة).
• إذا كانت المهمة على الأقل ، فلا توجد معاملات إيجابية في الصف الوظيفي (أي مع أي تغيير في المتغيرات ، لن تنخفض قيمة الوظيفة الناتجة).

2. وظائف غير محدودة

ومع ذلك ، تجدر الإشارة إلى أن وظيفة معينة قد لا تصل إلى الحد الأقصى / الحد الأدنى في منطقة معينة. يمكن صياغة السمة الجبرية لهذا على النحو التالي:

عند اختيار صف بادئة (متغير مستبعد) ، فإن نتيجة القسمة المتجهية للمتجه من الجانبين الأيمن حسب العمود بادئة تحتوي فقط على قيم صفرية وسلبية.

في الحقيقة ، هذا يعني أنه بغض النظر عن النمو الذي وضعناه لمتغير أساسي جديد ، فلن نجد قمة جديدة. لذلك ، لا تقتصر وظيفتنا على مجموعة من الحلول الممكنة.

3. حلول بديلة

عند العثور على الحل الأمثل ، يكون هناك خيار آخر ممكن - هناك حلول بديلة (نقطة ركن أخرى تعطي نفس القيمة الوظيفية).

علامة جبرية لوجود بديل:

بعد الوصول إلى الحل الأمثل ، لا توجد معاملات صفرية للمتغيرات المجانية في الصف الوظيفي.

هذا يعني أنه مع نمو المتغير المقابل ذي معامل الصفر ، لن تتغير قيمة الوظيفية وسيوفر الحل الأساسي الجديد أفضل الوظائف.

خاتمة

يهدف هذا المقال إلى فهم أعمق للجزء النظري. في التعليقات والتفسيرات هنا ، يمكنك الحصول على إجابات للأسئلة التي يتم حذفها عادةً عند دراسة هذه الطريقة واتخاذها مسبقًا. ومع ذلك ، يجب على المرء أن يفهم أن العديد من طرق التحسين العددي تستند إلى طريقة simplex (على سبيل المثال ، طريقة Gomori ، M-Method ) وبدون فهم أساسي ، من غير المحتمل أن يتم إحراز تقدم كبير في مزيد من الدراسة وتطبيق جميع خوارزميات هذه الفئة.

بعد ذلك بقليل ، سأكتب مقالًا عن التطبيق العملي لأسلوب البسيط ، بالإضافة إلى عدة مقالات حول طريقة المتغيرات الاصطناعية (طريقة M) وطريقة جوموري وطريقة الفرع والحدود.

شكرا لاهتمامكم!

PS

إذا كنت قد تعذبت بالفعل من تنفيذ طريقة البساطة ، فإنني أنصحك بقراءة كتاب أ. طه ، مقدمة لدراسة العمليات - يتم تحليل كل شيء جيدًا من الناحية النظرية والأمثلة على حد سواء ؛ وانظر أيضًا في أمثلة لحل مشاكل matburo.ru - هذا سيساعد في التنفيذ في التعليمات البرمجية.