آلان تورينج كتاب وملاحظة غامضة - العلوم المخبر

الترجمة الأصلية في مدونتي

كيف حصل هذا الكتاب علي؟

في مايو 2017 ، تلقيت رسالة بريد إلكتروني من أستاذي القديم بالمدرسة الثانوية يدعى جورج روتر ، والذي كتب فيه: " لدي نسخة من كتاب ألماني كبير من ديراك (Die Prinzipien der Quantenmechanik) ، الذي ينتمي إلى آلان تورينج ، وبعد ذلك بينما قرأت كتابك Idea Makers ، بدا لي أمراً مفروغاً منه أنك الشخص الذي يحتاجه ". أوضح لي أنه تلقى كتابًا من آخر (بحلول ذلك الوقت المتوفى) أستاذي في المدرسة نورمان روتليدج ، الذي عرفت أنه صديق ألان تورينج. اختتم جورج رسالته بعبارة: " إذا كنت بحاجة إلى هذا الكتاب ، فيمكنني تسليمه إليك في المرة القادمة التي تأتي فيها إلى إنجلترا ".

بعد عامين في مارس 2019 ، وصلت حقًا إلى إنجلترا ، وبعد ذلك اتفقت مع جورج على تناول وجبة الإفطار في فندق صغير في أكسفورد. أكلنا ، تجاذبنا أطراف الحديث وانتظر الطعام لتسوية. ثم جاءت اللحظة المناسبة لمناقشة الكتاب. وضع جورج يده في حقيبته واستخرج مجلداً أكاديمياً نموذجياً متواضعاً في منتصف القرن العشرين.



فتحت الغطاء ، وأتساءل عما إذا كان يمكن أن يكون على ظهر النقش: " ملكية آلان تورينج" أو شيء من هذا القبيل. لكن لسوء الحظ ، لم يكن الأمر كذلك. ومع ذلك ، تم إرفاق ملاحظة معبرة إلى حد ما على أربع أوراق من نورمان روتليدج إلى جورج روتر ، والتي كتبت في عام 2002.

كنت أعرف نورمان روتليدج عندما كنت لا أزال طالبًا في المدرسة الثانوية في إيتون في أوائل السبعينيات. كان مدرسًا للرياضيات يطلق عليه The Nutty Norman. لقد كان معلمًا رائعًا من جميع النواحي وروى قصصًا لا نهاية لها حول الرياضيات وجميع أنواع الأشياء الأخرى المثيرة للاهتمام. كان مسؤولاً عن ضمان تلقي المدرسة لجهاز كمبيوتر (مبرمجة بشريط مثقّب بعرض مكتب) - كان هذا أول جهاز كمبيوتر استعملته على الإطلاق .

في تلك الأيام ، لم أكن أعرف شيئًا عن ماضي نورمان (تذكر أن هذا كان قبل فترة طويلة من ظهور الإنترنت). كنت أعرف فقط أنه "دكتور روتليدج". غالبًا ما روى قصصًا عن أشخاص من كامبريدج ، لكنه لم يذكر آلان تورينج أبدًا في قصصه. بالطبع ، لم يكن تورينج مشهورًا بما فيه الكفاية في ذلك الوقت (رغم أنه ، كما اتضح ، سمعت عنه بالفعل من شخص عرفه في بلتشلي بارك (القصر الذي كان مركز التشفير يقع فيه خلال الحرب العالمية الثانية)).

لم يكن آلان تورينج مشهورًا حتى عام 1981 ، عندما بدأت لأول مرة في دراسة البرامج البسيطة ، على الرغم من أنني كنت في ذلك الوقت في سياق الأوتوماتة الخلوية ، وليس آلات تورينج .

فجأة في أحد الأيام ، نظرت إلى فهرس البطاقات في مكتبة معهد كاليفورنيا للتكنولوجيا ، تعثرت على كتاب آلان تورنج ، الذي كتبته والدته سارة تورينج. كان للكتاب الكثير من المعلومات ، بما في ذلك أعمال تورينج العلمية غير المنشورة في علم الأحياء. ومع ذلك ، لم أكن أتعلم شيئًا عن علاقته بنورمان روتليدج ، حيث أن الكتاب لم يذكر أي شيء عنه (على الرغم من أنني ، كما اكتشفت ، تتطابق سارة تورينج مع نورمان حول هذا الكتاب ، وحتى أن نورمان كتب مراجعة له في النهاية).



بعد مرور عشر سنوات ، قمت بزيارتها في أرشيف تورينج في كلية كينجز كوليدج في كامبريدج ، بعد عشر سنوات من رغبتي في فضول تورينج وعمله في علم الأحياء (الذي لم يتم نشره بعد). بعد فترة وجيزة ، بعد أن تعرفت على ما كان لديهم من عمل تورينج ، وقضيت بعض الوقت في ذلك ، اعتقدت أنه في نفس الوقت يمكنني أن أطلب منه أن يرى مراسلاته الشخصية أيضًا. من خلال البحث ، وجدت عدة رسائل من آلان تورينج إلى نورمان روتليدج.

بحلول ذلك الوقت ، تم نشر سيرة أندرو هودجز ، والتي فعلت الكثير حتى أصبح تورينج مشهورًا في النهاية ، وأكد أن آلان تورينج ونورمان روتليدج كانا صديقين بالفعل ، وأن تورينج كان أيضًا مستشارًا علميًا لنورمان. أردت أن أسأل روتلدج عن تورينج ، لكن بحلول ذلك الوقت كان نورمان قد تقاعد بالفعل وعاش حياة منعزلة. ومع ذلك ، عندما أكملت العمل في كتاب " نوع جديد من العلوم" في عام 2002 (بعد تراجعي عن العشر سنوات) ، قمت بتتبعه وأرسلته نسخة من الكتاب مع شرح "إلى معلم الرياضيات الأخير". ثم قابلنا بعض الشيء ، وفي عام 2005 جئت مجددًا إلى إنجلترا ووافقت على مقابلة نورمان لتناول فنجان من الشاي في فندق فاخر في وسط لندن.

كان لدينا حديث لطيف حول العديد من الأشياء ، بما في ذلك آلان تورينج. بدأ نورمان حديثنا مع القصة التي كان يعرفها حقًا عن تورينج ، معظمها كان سطحيًا ، قبل 50 عامًا. ولكن مع ذلك ، كان لديه ما يخبره به شخصيًا: " لقد كان غير قابل للانفصال ". " لقد ضحك كثيرا ". " لم يستطع التحدث مع غير علماء الرياضيات ". " كان دائمًا خائفًا من غضب والدته ". " غادر خلال النهار وركض ماراثون ." " لم يكن طموحاً للغاية ." ثم عاد الحديث إلى هوية نورمان. قال إنه على الرغم من أنه تقاعد بالفعل لمدة 16 عامًا ، فإنه لا يزال يكتب مقالات لصحيفة الرياضيات ، بحيث " يكمل ، حسب تعبيره ، جميع أعماله العلمية قبل الانتقال إلى عالم آخر " حيث ، كما أضاف مع ابتسامة بالكاد محسوسة ، " سيتم بالتأكيد كشف كل الحقائق الرياضية ." عندما انتهى حفل الشاي ، ارتدى نورمان سترته الجلدية وتوجه إلى مركبته ، متجاهلاً تمامًا التفجيرات التي عطلت حركة المرور في لندن في ذلك اليوم.

كانت هذه آخر مرة رأيت فيها نورمان ، وتوفي في عام 2013.

بعد ست سنوات ، جلست في الإفطار مع جورج روتر. كانت معي مذكرة من روتلدج ، كتبه عام 2002 بخط يده المميز:



في البداية قرأت الملاحظة بطلاقة. كانت معبرة كالمعتاد:

تلقيت كتابًا لألان تورينج من صديقه ومنفذه روبن غاندي (من كلية كينجز كوليدج ، كان من الطبيعي أن أعطي كتبًا من مجموعة من الرفاق المتوفين ، واخترت مجموعة من قصائد أ.د. هاوسمان من كتب إيفور رامزي كهدية مناسبة (كان العميد و قفز من الكنيسة [في عام 1956]) ...

في وقت لاحق في مذكرة قصيرة يكتب:

أنت تسأل ، في النهاية ، هل كان يجب أن يذهب هذا الكتاب - في رأيي ، يجب أن يذهب إلى شخص يقدر كل ما يتعلق بعمل تورينج ، لذلك يعتمد مصيره عليك.

أرسلني ستيفن ولفرام كتابه المثير للإعجاب ، لكنني لم أغوص فيه ...

في الختام ، هنأ جورج روتر على امتلاكه الشجاعة للانتقال (كما اتضح ، مؤقتًا) إلى أستراليا بعد تقاعده ، وقال إنه هو نفسه " سيلعب الانتقال إلى سريلانكا كمثال على وجود رخيص يشبه اللوتس ". لكنه أضاف أن " الأحداث التي تجري هناك تشير الآن إلى أنه لا ينبغي أن يفعل هذا " (على ما يبدو يشير إلى الحرب الأهلية في سري لانكا).

إذن ما الخفي في أحشاء الكتاب؟

لذا ، ماذا فعلت بنسخة من كتاب باللغة الألمانية كتبه بول ديراك كان ينتمي ذات مرة إلى آلان تورينج. أنا لا أقرأ الألمانية ، لكن لدي نسخة من نفس الكتاب باللغة الإنجليزية (وهي لغة النسخة الأصلية) من نسخة السبعينيات. ومع ذلك ، يبدو لي أنه بمجرد تناول وجبة الإفطار ، يجب عليّ أن أراجع بعناية صفحة الكتاب بصفحة. في النهاية ، هذه ممارسة شائعة عند التعامل مع الكتب القديمة.

تجدر الإشارة إلى أن دهشت من أناقة عرض ديراك. نُشر الكتاب في عام 1931 ، لكن شكليته البحتة (ونعم ، على الرغم من حاجز اللغة ، كان بإمكاني قراءة الرياضيات الموصوفة في الكتاب) تقريبًا كما لو كانت مكتوبة اليوم. (لا أريد التركيز أكثر من اللازم على ديراك هنا ، لكن صديقي ريتشارد فاينمان أخبرني أنه ، على الأقل في رأيه ، معرض ديراك أحادي الشكل. أخبرني نورمان روتليدج أنه كان صديقًا في كامبريدج مع ابن ديراك بالتبني ، والذي أصبح مناصريًا في غالبًا ما كان نورمان في منزل ديراك وقال إن "الرجل العظيم" تلاشى في بعض الأحيان شخصيًا في الخلفية ، بينما كان لدى المقدمة دائمًا الكثير من الألغاز الرياضية ، لكن لسوء الحظ لم أقابل بول ديراك مطلقًا. قيل لي أنه بعد ر واو ، عندما غادر كامبريدج أخيرًا وذهب إلى فلوريدا ، فقد معظم صلابته السابقة وأصبح شخصًا اجتماعيًا تمامًا).

ولكن العودة إلى كتاب ديراك ، الذي ينتمي إلى تورينج. في الصفحة 9 ، لاحظت تسطير وملاحظات الهامش الصغيرة مكتوبة بقلم رصاص بسيط. واصلت تقليب الصفحات. بعد عدة فصول ، اختفت الملاحظات. ولكن ، فجأة ، وجدت ملاحظة مضمنة في الصفحة 127 مع المحتوى التالي:



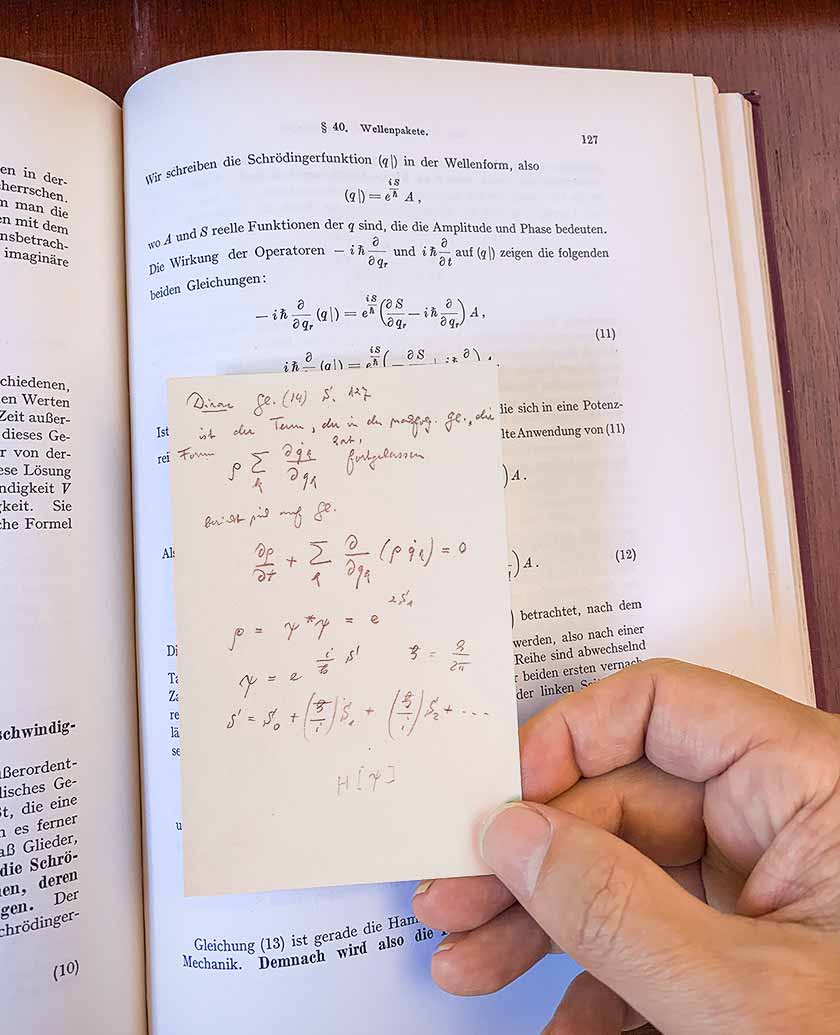
وقد كتب باللغة الألمانية بخط اليد الألماني القياسي. ويبدو أنه يمكن ربطه بطريقة أو بأخرى مع ميكانيكا لاغرانج . اعتقدت أنه ربما يكون شخص ما يمتلك هذا الكتاب قبل تورينج ، ويجب أن تكون هذه ملاحظة كتبها هذا الشخص.

واصلت ورقة من خلال الكتاب. لا توجد ملاحظات. وأعتقد أنه لم يعد بإمكاني العثور على أي شيء. ولكن بعد ذلك ، في الصفحة 231 ، وجدت إشارة الشركة - مع النص المطبوع:



هل سأجد في النهاية أي شيء آخر؟ واصلت ورقة من خلال الكتاب. ثم ، في نهاية الكتاب ، في الصفحة 259 ، في القسم الخاص بالنظرية النسبية للإلكترونات ، وجدت ما يلي:



لقد كشفت هذه الورقة:



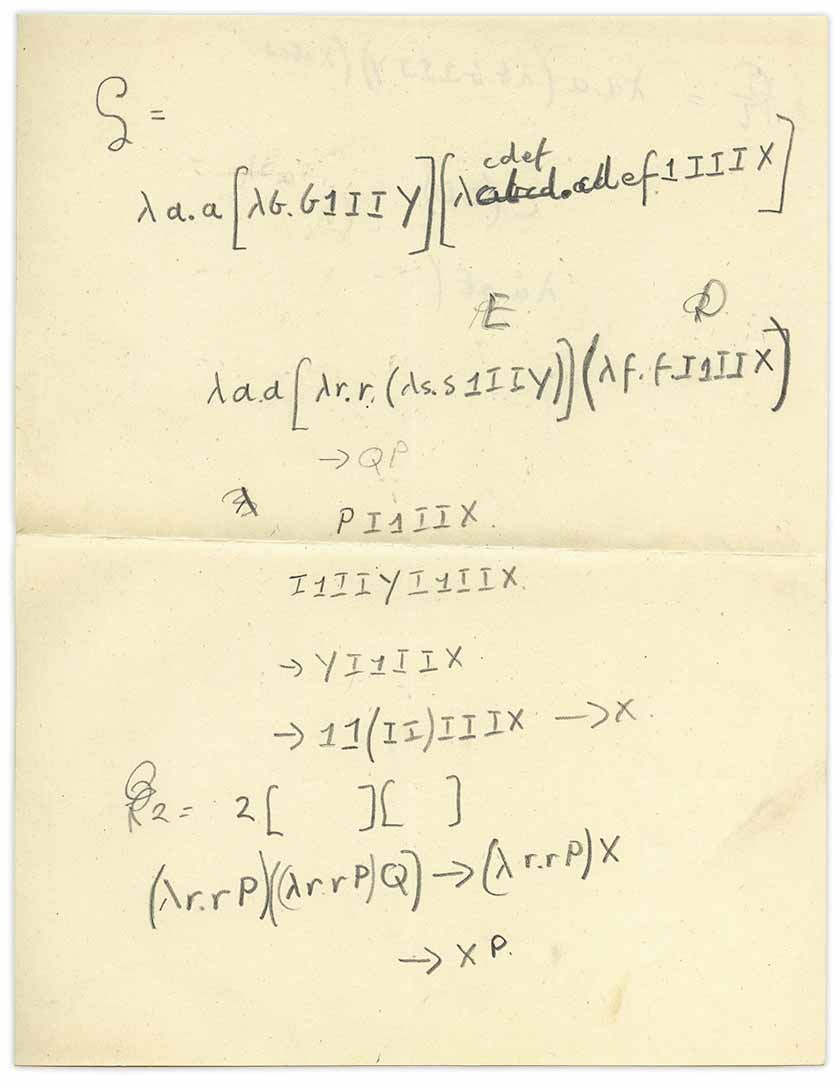
أدركت على الفور أن هذا كان حساب التفاضل والتكامل لامدا مع مزيج من combinators ، ولكن كيف ظهرت هذه الورقة هنا؟ تذكر أن هذا الكتاب هو كتاب عن ميكانيكا الكم ، ولكن الورقة المرفقة تتناول المنطق الرياضي ، أو ما يسمى الآن نظرية الحوسبة. هذا نموذجي لكتابات تورينج. تساءلت إذا كان تورينج شخصيا كتب هذه الملاحظة.

حتى أثناء وجبة الإفطار ، قمت بالبحث في الإنترنت عن عينات خط اليد من تورينج ، لكنني لم أجد أمثلة في شكل عمليات حسابية ، لذلك لم أتمكن من استخلاص استنتاجات حول الهوية الدقيقة لخط اليد. وسرعان ما اضطررت للذهاب. حزمت الكتاب بعناية ، وعلى استعداد للكشف عن سر ما كانت الصفحة ومن كتبه ، وأخذته معي.

عن الكتاب

بادئ ذي بدء ، دعونا نناقش الكتاب نفسه. تم نشر مبادئ ميكانيكا الكم بواسطة بول ديراك باللغة الإنجليزية في عام 1930 وتم ترجمتها قريبًا إلى الألمانية. (يرجع تاريخ Dirac إلى 29 مايو 1930 ؛ إنه ينتمي إلى المترجم Werner Bloch ، في 15 أغسطس 1930.) أصبح الكتاب علامة فارقة في تطوير ميكانيكا الكم ، حيث وضع منهجية شكلية واضحة لأداء الحسابات ، ومن بين أشياء أخرى ، شرح تنبؤات Dirac حول البوزيترون ، والتي ستكون افتتح في عام 1932.

لماذا ألان تورينج لديه كتاب باللغة الألمانية ، وليس الإنجليزية؟ لا أعرف هذا بالتأكيد ، ولكن في تلك الأيام كانت اللغة الألمانية هي اللغة الرائدة في العلوم ، ونحن نعلم أن آلان تورينج كان قادرًا على قراءتها. (بعد كل شيء ، في عنوان عمله الشهير آلة تورينج " حول الأرقام المحسوبة مع ملحق لمشكلة القرار (Entscheidungsproblem) "كانت كلمة ألمانية طويلة للغاية - وفي الجزء الرئيسي من المقال يعمل بأحرف قوطية غامضة في شكل" أحرف ألمانية "، والتي استخدمها بدلاً من الأحرف اليونانية على سبيل المثال).

آلان تورينج اشترى الكتاب بنفسه أم سلمه له؟ لا اعرف يوجد في الجزء الداخلي من غلاف كتاب تورينج تدوين بالقلم الرصاص "20 / -" ، والذي كان المدونة القياسية "20 شلن" ، على غرار £ 1. يوجد على الصفحة اليمنى "26.9.30" محو ، من المفترض أنه يعني 26 سبتمبر 1930 - ربما تاريخ شراء الكتاب لأول مرة. ثم ، في الزاوية اليمنى العليا ، الرقم المحو هو "20". ربما هذا هو الثمن مرة أخرى. (هل يمكن أن يكون هذا هو السعر في Reichsmarks ، إذا افترضنا أن الكتاب قد تم بيعه في ألمانيا؟ في ذلك الوقت ، كان 1 Reichsmark يستحق حوالي 1 شلن ، ومن المحتمل أن يكون السعر الألماني مكتوبًا مثل ، "20 RM".) أخيرًا ، على الجزء الداخلي من الغطاء الخلفي هو "c 5 / -" - ربما يكون (مع خصم كبير) ثمن كتاب مستعمل.

لنلقِ نظرة على التواريخ الرئيسية لحياة آلان تورينج. ولد آلان تورينج في 23 يونيو 1912 (من قبيل الصدفة ، بالضبط 76 سنة قبل Mathematica 1.0 ). في خريف عام 1931 ، دخل كلية الملك ، كامبريدج. حصل على درجة البكالوريوس بعد ثلاث سنوات من الدراسة القياسية ، في عام 1934.

في عشرينيات القرن العشرين وأوائل الثلاثينيات من القرن الماضي ، كانت ميكانيكا الكم موضوعًا ساخنًا ، وكان آلان تورينج مهتمًا بها بالتأكيد. نعلم من أرشيفه أنه في عام 1932 ، بمجرد نشر الكتاب ، تلقى " الأسس الرياضية لميكانيكا الكم " لجون فون نيومان (باللغة الألمانية ). نعلم أيضًا أنه في عام 1935 ، تلقى تورينج مهمة من فيزيائي كامبريدج رالف فاولر حول موضوع دراسة ميكانيكا الكم. (اقترح فاولر حساب ثابت العزل الكهربائي للماء ، وهي في الواقع مهمة صعبة للغاية ، تتطلب تحليلاً كاملاً مع نظرية مجال الكم المتفاعل ، والتي لم يتم حلها بعد بشكل كامل).

ومع ذلك ، متى وكيف حصل تورينج على نسخته من كتاب ديراك؟ بالنظر إلى أن الكتاب له سعر مكسور ، يزعم أن تورينج اشتراه بالفعل. من كان أول مالك للكتاب؟ يبدو أن الملاحظات الواردة في الكتاب تتعلق في المقام الأول بالهيكل المنطقي ، تجدر الإشارة إلى أن بعض العلاقات المنطقية ينبغي اعتبارها بديهية. ثم ماذا عن الملاحظة المرفقة في صفحة 127؟

حسنًا ، قد يكون هذا من قبيل الصدفة ، ولكن في الصفحة 127 فقط - يتحدث ديراك عن المبدأ الكمومي لأقل حركة ويضع الأساس لتكامل على طول مسار فاينمان - الذي هو أساس كل أشكال الكم الحديثة. ماذا تحتوي المذكرة؟ يحتوي على امتداد للمعادلة 14 ، وهو معادلة للتطور الزمني للسعة الكمومية. استبدل مؤلف المذكرة Dirac A من أجل السعة بـ possibly ، وربما يعكس السجل الألماني السابق (قياس الكثافة السائلة). ثم يحاول المؤلف توسيع العمل بصلاحيات ℏ ( ثابت Planck مقسومًا على 2π ، والذي يسمى أحيانًا ثابت Dirac ).

ولكن يبدو أنه من بين ما يرد في الصفحة ، هناك القليل الذي يمكن تعلمه. إذا أبقت الصفحة في الضوء ، فهي تحتوي على مفاجأة صغيرة - علامة مائية عليها نقش "Z f. PHYSIK. علم. ب ":



هذه نسخة مختصرة من مجلة Zeitschrift für physikalische Chemie ، و Abteilung B ، المجلة الألمانية للكيمياء الفيزيائية ، التي نشرت منذ عام 1928. ربما كتبت المذكرة بواسطة محرر المجلة؟ هنا هو عنوان المجلة لعام 1933. مريح ، يتم سرد المحررين مع موقعهم ، واحد منهم تبرز: "ولد · كامبريدج".



هذا هو ماكس بورن وهو مؤلف حكم بورن وأكثر من ذلك بكثير في نظرية ميكانيكا الكم (وكذلك جد المغنية أوليفيا نيوتن جون ). لذلك ، قد تكون كتبت هذه المذكرة من قبل ماكس بورن؟ لكن ، لسوء الحظ ، هذا ليس كذلك ، لأن خط اليد لا يتطابق.

ماذا عن الإشارات المرجعية في الصفحة 231؟ هنا هو من الجانبين:



المرجعية غريبة وجميلة. ولكن متى تم صنعه؟ هناك مكتبة هيفرز في كامبريدج ، على الرغم من أنها الآن جزء من بلاكويل. لأكثر من 70 عامًا (حتى عام 1970) ، كان موقع Heffers في العنوان ، كما تظهر الإشارة المرجعية ، 3 و 4 بواسطة Petty Cury .

تحتوي علامة التبويب هذه على مفتاح مهم - هذا هو رقم الهاتف. 862. " اتضح أنه في عام 1939 تحولت معظم كامبريدج (بما في ذلك Heffers) إلى أرقام من أربعة أرقام ، وبطبيعة الحال ، بحلول عام 1940 طبعت الإشارات المرجعية بأرقام هواتف "حديثة". (ازدادت أرقام الهواتف الإنجليزية تدريجيًا ؛ وعندما نشأت في إنجلترا في الستينيات ، كانت أرقام هواتفنا هي Oxford 56186 و Kidmore End 2378. جزئيًا ، أتذكر هذه الأرقام لأن الغريب أنها الآن لم يبدو ، لقد اتصلت دائمًا برقم هاتفي عند الرد على مكالمة واردة).

تمت طباعة الإشارة المرجعية في هذا النموذج حتى عام 1939. لكن كم من الوقت قبل ذلك؟ يمكنك العثور على عدد قليل من عمليات المسح لإعلانات Heffers القديمة على الإنترنت ، على الأقل منذ عام 1912 (إلى جانب "نطلب منك تلبية طلباتك ...") يضيفون "هاتف 862" ، مضيفين "(خطان)". هناك أيضًا بعض الإشارات المرجعية ذات التصميم المماثل التي يمكن العثور عليها في الكتب منذ عام 1904 (على الرغم من أنه ليس من الواضح ما إذا كانت أصلية لهذه الكتب (أي ، المطبوعة في نفس الوقت). لأغراض تحقيقنا ، يبدو أننا يمكن أن نستنتج أنه جاء هذا الكتاب من متجر هيفرز (الذي كان بالمناسبة المتجر الرئيسي في كامبريدج) في وقت ما بين عامي 1930 و 1939.

صفحة مع حساب التفاضل والتكامل لامدا

نحن الآن نعرف شيئًا عن وقت شراء الكتاب. ولكن ماذا عن "صفحة حساب التفاضل والتكامل لامدا"؟ متى كتب هذا؟ حسنًا ، بالطبع ، بحلول ذلك الوقت ، كان لابد من اختراع حساب التفاضل والتكامل. وقد تم ذلك بواسطة ألونزو تشيرش ، عالم الرياضيات من برينستون ، في شكله الأصلي في عام 1932 وفي شكله النهائي في عام 1935. (كانت هناك أعمال قام بها علماء أسلافهم ، لكنهم لم يستخدموا الرمز λ).

هناك علاقة معقدة بين آلان تورينج وحساب التفاضل والتكامل لامدا. في عام 1935 ، أصبح تورينج مهتمًا بـ "ميكنة" العمليات الرياضية ، واخترع فكرة استخدام آلة تورينج لحل مشاكل أسس الرياضيات. أرسل تورينج مقالاً حول هذا الموضوع إلى المجلة الفرنسية ( Comptes rendus ) ، لكنه ضاع في البريد ؛ ثم اتضح أن المرسل إليه الذي أرسلها إليها ما زال غير موجود ، حيث كان قد نقل الصين.

لكن في مايو 1936 ، وحتى قبل إرسال تورينج لمقاله في مكان آخر ، وصل عمل كنيسة ألونزو من الولايات المتحدة . , 1934 , , , 1922 .
, - , ( - ). ( ) , , . 1936 ( ) « …» .

: 1936 1938 ( 1937 ) , , . , -, — , - , — , , .

1938 , , -, , . 1945 , . 1947–8 , , .

1951 . ( , , , , - , ). , 1954 , : « » ( : « , »). , , 7 1954 , . ( , , .)

, -. , :



, , , . ? , , , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .

?

لذلك ، دعونا نلقي نظرة فاحصة على ما هو على جانبي الورقة. لنبدأ مع lambdas.

فيما يلي طريقة لتعريف الدالات "الخالصة" أو "المجهولة" ، وهي المفهوم الأساسي في المنطق الرياضي ، والآن في البرمجة الوظيفية. هذه الوظائف شائعة جدًا في لغة Wolfram ، ومن السهل شرح وظيفتها. على سبيل المثال ، يكتب شخص ما f [ x ] للإشارة إلى الدالة f المطبقة على الوسيطة x. وهناك العديد من وظائف f المسماة مثل Abs أو Sin أو Blur . ولكن ماذا لو أراد شخص ما أن يكون [ x ] 2 × 1 ؟ لا يوجد اسم فوري لهذه الوظيفة. ولكن هل هناك شكل آخر من أشكال المهمة ، و [ س ]؟

الجواب نعم: بدلاً من f نكتب Function[a,2a+1] . وفي لغة Function [a,2a+1][x] Wolfram Function [a,2a+1][x] تطبق الدوال على الوسيطة x ، مما يؤدي إلى 2x+1 كنتيجة لذلك. Function[a,2a+1] هي وظيفة "نقية" أو "مجهولة" ، وهي عملية نقية للتكاثر في 2 وإضافة 1.

لذلك ، calcul في حساب التفاضل والتكامل lambda هو التماثل الدقيق للوظيفة في لغة Wolfram - وبالتالي ، على سبيل المثال ، λ a (2 a + 1) مكافئ Function[a, 2a + 1] . (تجدر الإشارة إلى أن الوظيفة ، على سبيل المثال ، Function[b,2b+1] مكافئة ؛ "المتغيرات ذات الصلة" a أو b هي مجرد أماكن لاستبدال وسيطة الوظيفة - وفي Wolfram Language يمكن تجنبها باستخدام خيارات بديلة لتحديد دالة محض (2# +1)& ).

في الرياضيات التقليدية ، تُعتبر الدوال عادة ككائنات تعرض بيانات الإدخال (على سبيل المثال ، أعداد صحيحة) ومخرجات البيانات (والتي هي أيضًا ، على سبيل المثال ، أعداد صحيحة). ولكن ما هو كائن الدالة (أو λ)؟ في جوهرها ، هذا هو المشغل الهيكلي الذي يأخذ التعبيرات ويحولها إلى وظائف. قد يبدو هذا غريبًا بعض الشيء من حيث الرياضيات التقليدية والشكل الرياضي للكتابة ، ولكن إذا احتاج شخص ما إلى التعامل مع الشخصيات التعسفية ، وهو أمر طبيعي للغاية ، حتى لو بدا في البداية مجردة بعض الشيء. (تجدر الإشارة إلى أنه عندما يتعلم المستخدمون لغة Wolfram ، يمكنني دائمًا أن أقول أنهم تغلبوا على عتبة معينة من التفكير التجريدي عندما يحصلون على فكرة الوظيفة ).

Lambdas ليست سوى جزء مما هو موجود على الصفحة. هناك مفهوم آخر ، أكثر تجريدًا - فهذه أدوات دمج . النظر في خط PI1IIx غامضة إلى حد ما؟ ماذا يعني هذا؟ في الواقع ، هذا هو سلسلة من توليفات ، أو بعض التكوين التجريدي للوظائف الرمزية.

يمكن كتابة التراكب المعتاد للوظائف ، المألوف جدًا في الرياضيات ، بلغة ولفرام في الشكل: f[g[x]] - مما يعني "تطبيق f على نتيجة تطبيق g إلى x ". ولكن هل هناك حاجة إلى أقواس لهذا الغرض؟ في Wolfram ، f@g@ x هو شكل بديل من الرموز. في هذا المنشور ، نعتمد على تعريف Wolfram Language: العامل @ مرتبط بالجانب الأيمن ، لذلك f@g@x مكافئ لـ f@(g@x) .

ولكن ماذا يعني الإدخال (f@g)@x ؟ هذا يعادل f[g][x] . وإذا كانت f و g دالتين عاديتين في الرياضيات ، فستكون هذه بلا فائدة ، ولكن إذا كانت f هي وظيفة مرتبة أعلى ، فيمكن أن تكون f[g] نفسها دالة يمكن تطبيقها بشكل جيد على x .

لاحظ هنا لا يزال هناك بعض التعقيد. في f[] - f دالة من وسيطة واحدة. و f[] مكافئ لكتابة Function[a, f[a]][x] . ولكن ماذا عن وظيفة حجة اثنين ، على سبيل المثال ، f[x,y] ؟ يمكن كتابة هذا Function[{a,b},f[a, b]][x, y] . ولكن ماذا عن Function[{a},f[a,b]] ؟ ما هذا هناك "متغير حر" ب ، والذي يتم تمريره ببساطة إلى الوظيفة. Function[{b},Function[{a},f[a,b]]] سوف تربط هذا المتغير ، ثم Function[{b},Function[{a},f [a, b]]][y][x] يعطي f[x,y] مرة أخرى. (تعيين الوظيفة بحيث تحتوي على وسيطة واحدة تسمى "الكاري" تكريما للعالم المنطقي المسمى هاسكل كوري ).

إذا كانت المتغيرات الحرة موجودة ، فهناك العديد من الصعوبات المختلفة فيما يتعلق بكيفية تحديد الدوال ، ولكن إذا حصرنا أنفسنا في الدوال أو الكائنات التي لا تحتوي على متغيرات مجانية ، فيمكن تحديدها بحرية. وتسمى هذه الأشياء الموحدات.

المجمعات لها تاريخ طويل. من المعروف أنه تم اقتراحها لأول مرة في عام 1920 من قبل تلميذ ديفيد جيلبرت ، موسى شونفينكل .

في ذلك الوقت ، اكتشف مؤخرًا أنك لا تحتاج إلى استخدام تعبيرات و ، و / أو لا لتمثيل التعبيرات في منطق الاقتراح القياسي: كان يكفي استخدام المشغل الوحيد ، الذي سنطلق عليه الآن اسم Nand (لأنه ، على سبيل المثال ، إذا كتبنا Nand كـ · ، ثم Or[a,b] يأخذ النموذج (أ · أ) · (ب · ب) ). أراد Schönfinkel أن يجد نفس تمثيل الحد الأدنى للمنطق الأصلي ، أو المنطق الأساسي ، بما في ذلك الوظائف.

جاء مع اثنين من "الدمج" S و K. في Wolfram Language ، هذا مكتوب كـ
K [x _] [y_] → x و S [x _] [y _] [z_] → x [z] [y [z]].

من الجدير بالذكر أنه كان من الممكن استخدام هذين الجمعين لإجراء أي حسابات. هكذا على سبيل المثال

S [K [S]] [S [K [S [K [S]]]] [S [K [K]]]]

يمكن استخدامها كدالة لإضافة اثنين من الأعداد الصحيحة.

كل هذه الأمور ، بعبارة ملطفة ، هي كائنات مجردة إلى حد ما ، ولكن الآن بعد أن أدركنا ما هي آلات تورينج وحساب التفاضل والتكامل لامدا ، يمكننا أن نرى أن مزج Schoenfinkel توقع بالفعل مفهوم الحوسبة العالمية. (والأهم من ذلك ، أن تعاريف S و K لعام 1920 بسيطة للغاية ، وتشبه آلة تورينج العالمية البسيطة للغاية التي اقترحتها في التسعينيات ، والتي تم إثبات عالميتها في عام 2007 ).

لكن العودة إلى المنشور والخط PI1IIx . الأحرف المسجلة هنا هي أدوات دمج ، وكلها مصممة لتحديد الوظيفة. التعريف هنا هو أن تراكب الوظائف يجب أن يكون مترابطًا يسارًا ، لذا لا ينبغي تفسير fgx على أنه f @ g @ x أو f @ (g @ x) أو f [g [x]] ، ولكن بدلاً من ذلك (f @ g )x أو f [g] [x]. سوف نترجم هذا الإدخال إلى تنسيق مناسب للاستخدام من قبل Wolfram Language: PI1IIx سيأخذ النموذج p [i] [one] [i] [i] [x] .

لماذا تكتب شيئًا كهذا؟ لشرح هذا ، نحتاج إلى مناقشة مفهوم أرقام الكنيسة (سميت باسم كنيسة ألونزو). دعنا نقول أننا نعمل فقط مع الرموز ومع lambdas أو مجمعات. هل هناك طريقة لاستخدامها لتحديد أعداد صحيحة؟

ماذا عن مجرد قول أن الرقم n يتوافق مع Function[x, Nest[f,x,n]] ؟ أو بعبارة أخرى ، هذا (في أقصر الرموز):

1 هو f[#]&
2 هو f[f[#]]&
3 هو f[f[f[#]]]& وهكذا.

قد يبدو كل هذا أكثر غموضًا إلى حد ما ، لكن السبب في الاهتمام به هو أنه يسمح لنا بأن نفعل كل شيء رمزيًا وتجريديًا تمامًا ، دون الاضطرار إلى التحدث صراحة عن شيء مثل الأعداد الصحيحة.

باستخدام هذه الطريقة لتحديد الأرقام ، تخيل ، على سبيل المثال ، إضافة رقمين: 3 يمكن تمثيلهما كـ f[f[f[#]]]& 2 هي f[f[#]]& . يمكنك إضافتهم ببساطة عن طريق تطبيق واحد منهم على الآخر:



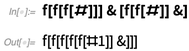
ولكن ما هو مثل و ؟ يمكن أن يكون أي شيء! بمعنى ما ، "انتقل إلى lambda" إلى النهاية وقم بتمثيل الأرقام باستخدام الوظائف التي تأخذ f كوسيطة. بمعنى آخر ، تخيل 3 ، على سبيل المثال ، مثل Function[f,f[f[f[#]]] &] أو Function[f,Function[x,f[f[f[x]]]] . (متى وكيف تحتاج إلى تسمية المتغيرات هو المصيد في حساب التفاضل والتكامل لامدا).

فكر في جزء من ورقة تورينج لعام 1937 بعنوان "القابلية للحساسية والانتشار" ، والتي تضع الأشياء كما ناقشنا للتو:



هنا ، قد يكون التسجيل مربكا إلى حد ما. Turing's x هو حرفنا f ، و x ' (ارتكب المسبب خطأ من خلال إدخال مسافة) هي x الخاصة بنا. ولكن هنا يتم استخدام نفس النهج بالضبط.

لذلك ، دعونا ننظر إلى الخط مباشرة بعد الطي أمام الورقة. هذا هو I1IIYI1IIx . وفقًا لشكل لغة Wolfram ، ستكون هذه i[one][i][i][y][i][one][i][i][x] . لكنني هنا دالة متطابقة ، لذلك i[one] تُرجع دالة i[one] فقط. وفي الوقت نفسه ، واحد هو تمثيل الكنيسة الرقمي ل 1 أو Function[f,f[#]&] . ولكن مع هذا التعريف ، يصبح one[] a[#]& one[a][b] يصبح a[b] . (بالمناسبة ، i[][b] ، أو Identity[][b] أيضًا [b] ).

سيكون الأمر أكثر وضوحًا إذا كتبنا قواعد الاستبدال لـ i و one ، بدلاً من استخدام حساب التفاضل والتكامل lamda مباشرة. والنتيجة ستكون هي نفسها. طبق هذه القواعد بشكل صريح ، نحصل على:



وهذا هو نفسه كما هو معروض في السجل المختصر الأول:



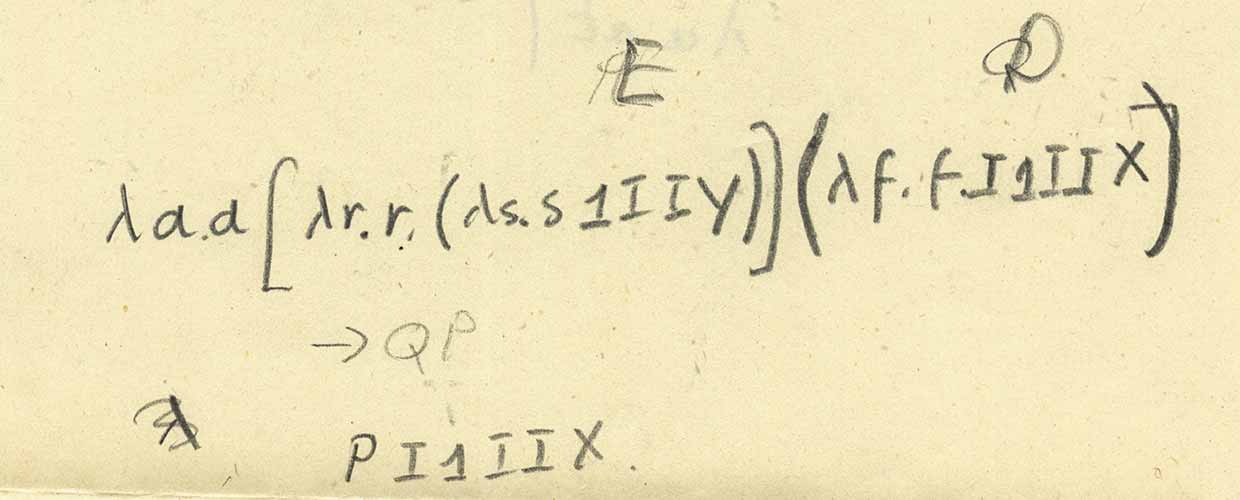
دعنا الآن ننظر إلى الورقة مرة أخرى ، في الجزء العلوي:



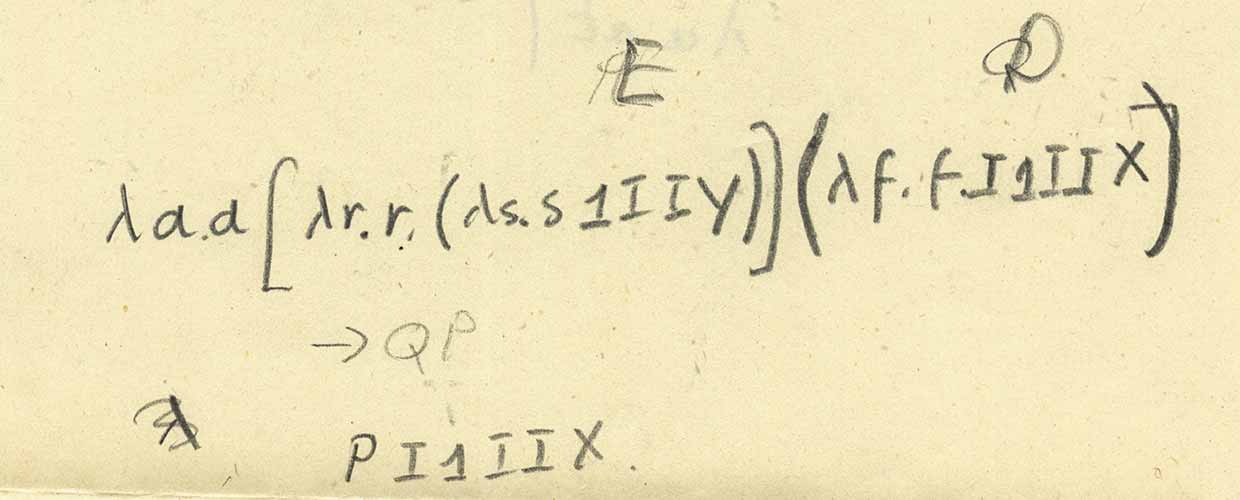
يوجد هنا أشياء مربكة وغير مفهومة "E" و "D" ، ولكن بواسطتها نعني "P" و "Q" ، حتى نتمكن من كتابة التعبير وحسابه (لاحظ أنه هنا - بعد بعض الالتباس مع الأخير الرمز - يضع "العالم الغامض" [...] و (...) لتمثيل وظائف التطبيق):



لذلك هذا هو أول اختصار هو مبين. لمعرفة المزيد ، دعنا نضع تعريفات بديلة لـ Q:



نحصل على الاختصار التالي الموضح بالضبط. ماذا يحدث إذا استبدلنا التعبيرات لـ P؟



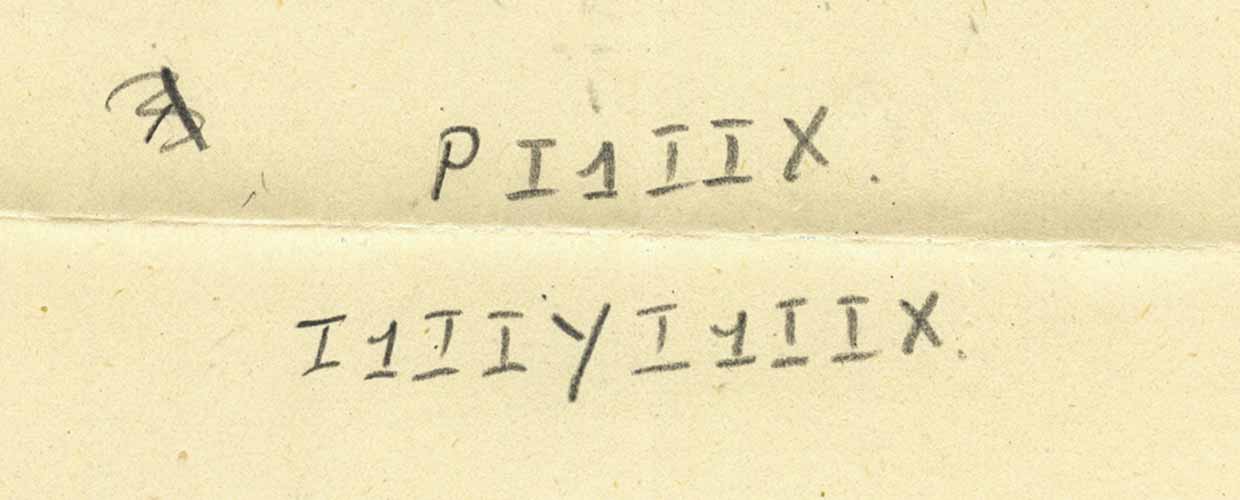
هذه هي النتيجة:



والآن ، باستخدام حقيقة أنني وظيفة تنتج الوسيطة نفسها ، نحصل على:



Oooops! ولكن هذا ليس هو السطر المسجل التالي. هل هناك خطأ هنا؟ هذا غير واضح. لأنه ، في النهاية ، على عكس معظم الحالات الأخرى ، لا يوجد سهم يشير إلى أن السطر التالي يتبع السطر السابق.

إليك نوعًا من الغموض ، ولكن دعنا ننتقل إلى أسفل المنشور:



هنا 2 هو رقم الكنيسة ، المعرفة ، على سبيل المثال ، من خلال النموذج two[a_] [b_] → a[a[b]] . لاحظ أن هذا هو في الواقع شكل السطر الثاني إذا تم التعامل مع a Function[r,r[]] و b كـ q . لذلك ، نتوقع أن تكون نتيجة الحسابات كما يلي:



ومع ذلك ، يمكن كتابة التعبير [b] الموجود في الداخل كـ x (ربما يختلف عن x المكتوب مسبقًا على الورقة) - ونتيجة لذلك ، نحصل على النتيجة النهائية:



لذا ، يمكننا فك تشفير القليل مما يحدث في هذه الورقة ، ولكن هناك لغز واحد على الأقل لا يزال هو ما يجب أن تكون عليه Y.

في الواقع ، يحتوي المنطق التوافقي على Combinator Y قياسي: ما يسمى بجمع النقاط الثابتة . بشكل رسمي ، يتم تعريفه بحقيقة أن Y [ f ] يجب أن تكون مساوية لـ f [Y [ f ]] ، أو بمعنى آخر ، Y [ f ] لا تتغير عند تطبيق f ، لذلك هذه نقطة ثابتة لـ f . (يرتبط Combinator Y بـ # 0 في Wolfram Language.)

حاليًا ، أصبح Y-combinator مشهورًا بفضل مسرّع الإطلاق Y-Combinator ، المسمى Paul Graham (الذي كان لفترة طويلة من محبي البرمجة الوظيفية ولغة برمجة LISP ونفذ أول متجر ويب يستند إلى هذه اللغة). قال لي ذات مرة: " لا أحد يفهم ما هو ص" الجمع ". (تجدر الإشارة إلى أن Y Combinator هو بالضبط ما يسمح للشركات بتجنب عمليات النقاط الثابتة ...)

تم اختراع Combinator Y (مثل Combinator ذو النقاط الثابتة) عدة مرات. جاء تورينج بالفعل مع تنفيذه في عام 1937 ، والذي أطلق عليه اسم Θ. ولكن هل الحرف "Y" على صفحتنا عبارة عن مُزج بين النقاط الثابتة الشهيرة؟ ربما لا. إذن ما هو "ص" لدينا؟ النظر في هذا التخفيض:



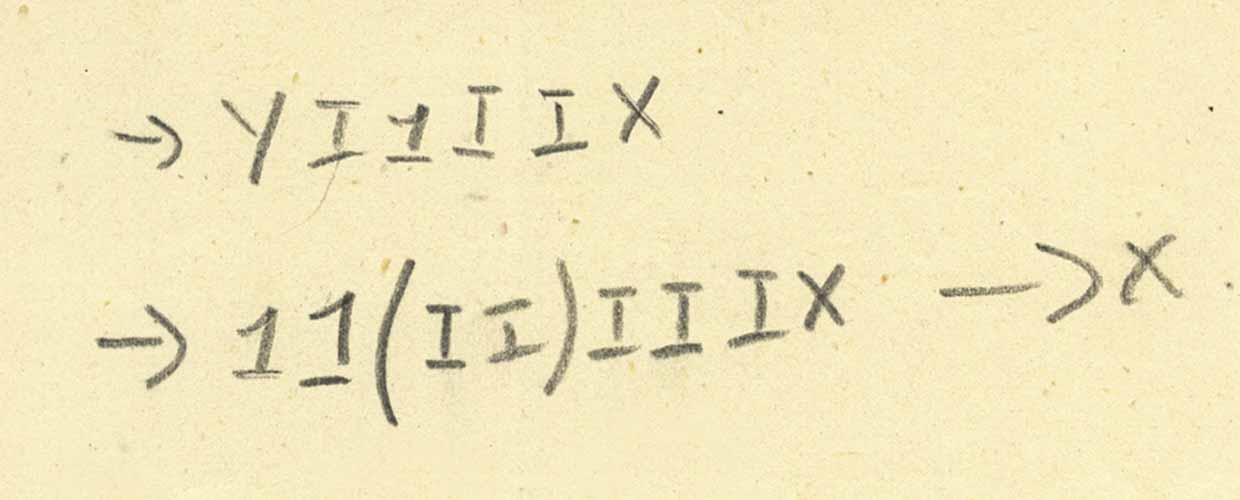
لكن من الواضح أن هذه المعلومات لا تكفي لتحديد ماهية Y بشكل لا لبس فيه ، ومن الواضح أن Y لا تعمل بحجة واحدة فقط ؛ يبدو أن الأمر يتعلق بحجتين على الأقل ، لكن من غير الواضح (على الأقل بالنسبة لي) عدد الحجج التي يتطلبها الإدخال وما الذي يفعله.

أخيرًا ، على الرغم من أننا يمكن أن نفهم أجزاء كثيرة من المنشور ، يجب أن نقول إنه على نطاق عالمي ليس من الواضح ما الذي تم فعله بشأنه. على الرغم من أنه يتطلب الكثير من التوضيحات لما يتم تقديمه على الورقة ، إلا أنه أساسي تمامًا في حساب التفاضل والتكامل lambda واستخدام المجمعات.

من المفترض ، هنا محاولة لإنشاء "برنامج" بسيط - باستخدام حساب التفاضل والتكامل lambda ومولمات من أجل القيام بشيء ما. لكن بقدر ما يكون هذا أمرًا معتادًا بالنسبة للهندسة العكسية ، فمن الصعب علينا أن نقول ما يجب أن يكون عليه هذا "الشيء" وما الهدف المشترك "القابل للتفسير".

هناك ميزة أخرى معروضة على الورقة ، والتي تستحق التعليق هنا - وهي استخدام أنواع مختلفة من الأقواس. في الرياضيات التقليدية ، تُستخدم الأقواس بشكل أساسي في كل شيء - وتطبيقات دالة (كما في f (x) ) ، وتجمعات الأعضاء (كما في (1 + x) (1 - x) ، أو أقل وضوحًا ، (1 - خ) ). (في لغة Wolfram ، نفصل بين الاستخدامات المختلفة للأقواس - بين أقواس مربعة لتحديد وظائف f [x] - والأقواس تستخدم فقط للتجميع).

عندما ظهر lambda calculus لأول مرة ، كان هناك العديد من الأسئلة حول استخدام الأقواس. في وقت لاحق ، كتب آلان تورينج عملاً كاملاً (غير منشور) بعنوان " تحويل الشكل الرياضي للتدوين والعبارات " ، لكنه شعر بالفعل في عام 1937 أنه بحاجة إلى وصف التعاريف الحديثة (بدلاً من القرصنة) لحساب التفاضل والتكامل في lambda (والتي ظهرت ، بالمناسبة ، من للكنيسة).

وقال إنه يجب كتابة f المطبق على g {f} (g) ، ما لم تكن f هي الشخصية الوحيدة ، وفي هذه الحالة يمكن أن تكون f (g) . ثم قال إنه يجب كتابة لامدا (كما في Function[a, b] ) على أنها " أ" [ ب ] أو ، بدلاً من ذلك ، " أ" . ب .

ومع ذلك ، ربما بحلول عام 1940 ، تم تجاهل الفكرة الكاملة لاستخدام {...} و [...] للإشارة إلى كائنات مختلفة ، خاصة لصالح الأقواس بأسلوب رياضي قياسي.

ألقِ نظرة على الجزء العلوي من الصفحة:



في هذا النموذج ، من الصعب فهمه. في تعريفات الكنيسة ، الأقواس المربعة مخصصة للتجميع ، مع وجود قوس فتح يحل محل فترة. باستخدام هذا التعريف ، يصبح من الواضح أن Q (المسمى أخيرًا D) ، والمضمنة بين قوسين في النهاية ، هو ما تنطبق عليه lambda بالكامل.

في الواقع ، قوس مربع هنا لا يحد من جسم لامدا. بدلاً من ذلك ، فإنه يمثل في الواقع تطبيقًا آخر للوظيفة ، وليس هناك إشارة واضحة إلى أين ينتهي جسم لامدا. في النهاية ، يمكن ملاحظة أن "العالم الغامض" قد غيّر قوس مربع الإغلاق إلى جولة واحدة ، وبالتالي طبق تعريف الكنيسة بفعالية - وأجبره على حساب التعبير ، كما هو موضح في الورقة.

إذن ماذا تعني هذه القطعة الصغيرة على أي حال؟ أعتقد أن هذا يشير إلى أن الصفحة كانت مكتوبة في ثلاثينيات القرن العشرين ، أو بعد ذلك بفترة طويلة ، لأن أسطورة الأقواس لم تستقر بعد.

إذن من الذي كان خط اليد؟

لذلك ، قبل ذلك تحدثنا عن ما هو مكتوب على الصفحة. ولكن ماذا عن الشخص الذي كتب كل شيء؟

المرشح الأكثر وضوحا لهذا الدور سيكون آلان تورينج نفسه ، لأن الصفحة كانت داخل كتابه. فيما يتعلق بالمحتوى ، يبدو أنه لا يوجد شيء يتعارض مع حقيقة أن آلان تورينج يمكنه كتابة هذا - حتى في الوقت الذي بدأ فيه التعامل مع حساب التفاضل والتكامل لامدا بعد أن حصل على مقال تشرش في أوائل عام 1936.

ماذا عن الكتابة اليدوية؟ هل تنتمي إلى آلان تورينج؟ خذ بعين الاعتبار العديد من العينات التي بقيت على قيد الحياة ، والتي ، كما نعلمها بالتأكيد ، كتبها آلان تورينج:



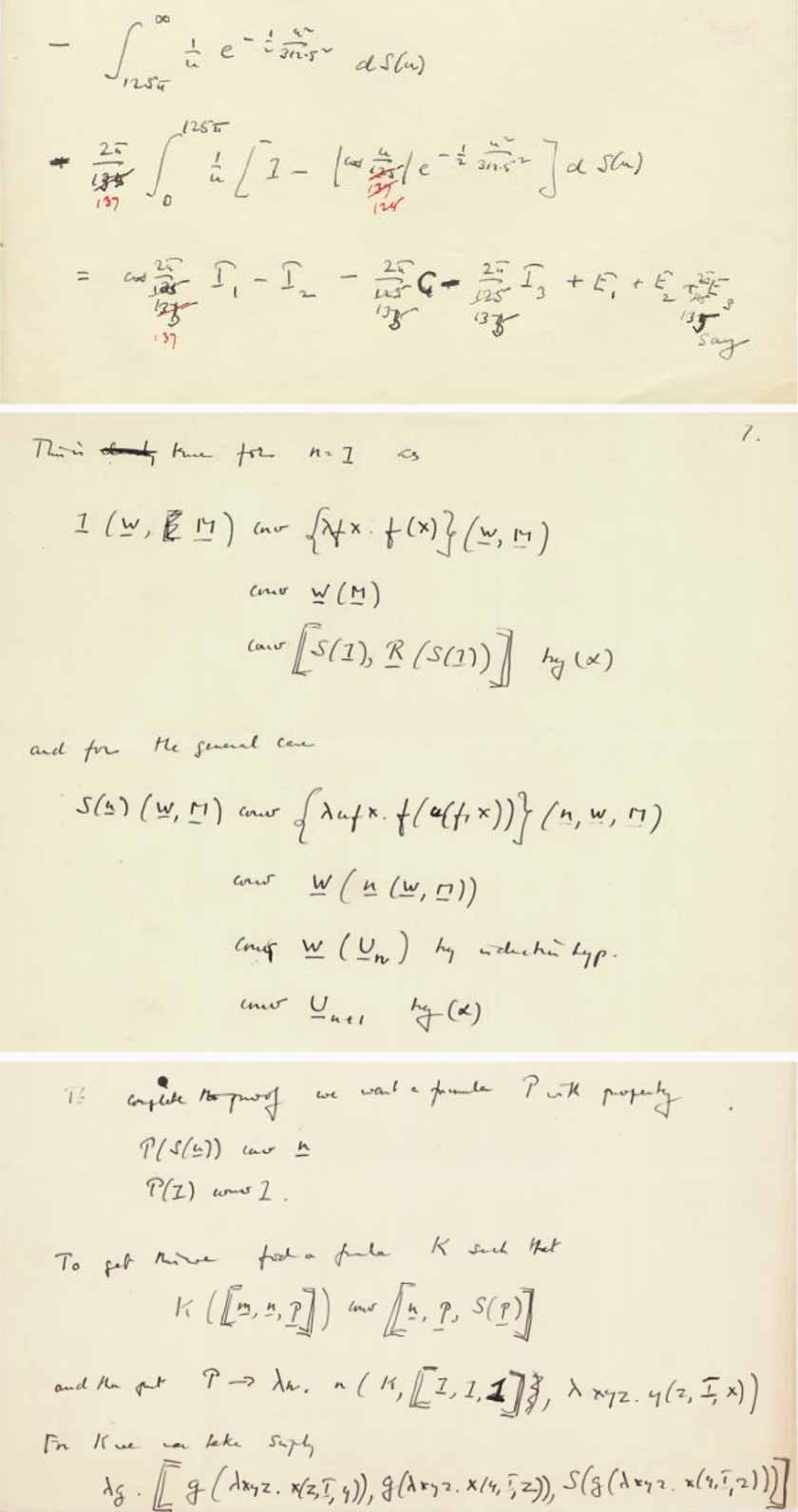
يبدو النص المقدم مختلفًا تمامًا ، لكن ماذا عن الترميز المستخدم في النص؟ على الأقل ، في رأيي ، لا يبدو هذا واضحًا جدًا - ويمكن الافتراض أن أي اختلاف يمكن أن يحدث بسبب حقيقة أن العينات الموجودة (المقدمة في الأرشيفات) مكتوبة ، إذا جاز التعبير ، "في النهاية" ، بينما لدينا الصفحة هي انعكاس لعمل الفكر.

اتضح أنه من المريح للتحقيق الذي أجريناه أن هناك صفحة في أرشيف تورينج كتب فيها جدولًا من الشخصيات اللازمة للتدوين. وعند مقارنة هذه الأحرف حرفًا بحرف ، فإنها تبدو مشابهة لي تمامًا (تم إجراء هذه السجلات أثناء فترة تورينج عندما كان يدرس نمو النبات ، ومن هنا ظهرت ملاحظة "مساحة الورقة"):



كنت أرغب في التحقق من ذلك بشكل أكثر عمقًا ، لذا قمت بإرسال عينات إلى شيلا لوي ، خبيرة الكتابة اليدوية (ومؤلفة خط اليد) ، الذين قابلتهم مرة واحدة - فقط أعرض الورقة الخاصة بنا كـ "نموذج A" وكتابة خط اليد الموجودة في Turing كـ "عينة" ب ". كانت إجابتها نهائية وسلبية: " أسلوب الكتابة مختلف تمامًا. بالنسبة إلى الشخصية ، لدى مؤلف العينة "B" طريقة تفكير أسرع وأكثر سهولة من مؤلف العينة "A ".

لم أكن مقتنعا تماما بهذا ، لكنني قررت أن الوقت قد حان للبحث عن خيارات أخرى.

لذلك إذا اتضح أن تورينج لم يكتب هذا ، فمن فعل ذلك؟ أخبرني نورمان روتليدج أنه تلقى الكتاب من روبن غاندي ، الذي كان منفذاً لتورينج. لذلك أرسلت "نموذج" C "" من غاندي:



ولكن استنتاج شيلا الأولي كان أن العينات الثلاثة ربما تكون مكتوبة من قبل ثلاثة أشخاص مختلفين ، مشيرة مرة أخرى إلى أن العينة "B" تم الحصول عليها من " المفكر الأسرع - الشخص الأكثر بحثًا عن حلول غير عادية للمشاكل " . (أجد أنه من الجيد أن يقوم أخصائي خط اليد الحديث بتقديم تقييم للكتابة اليدوية لخط تورينج ، بالنظر إلى مدى نشاط الجميع في واجبات تورينج المدرسية في العشرينيات من القرن الماضي).

حسنًا ، في تلك اللحظة ، بدا أن كلا من تورينج وغاندي تم استبعادهما من قائمة "المشتبه بهم". فمن يستطيع أن يكتب هذا؟ بدأت أفكر في الأشخاص الذين يستطيع تورينج إقراض كتابه. بالطبع ، في نفس الوقت ، يجب أن يكونوا قادرين على إجراء العمليات الحسابية باستخدام حساب lambda calculus.

اقترحت أن يكون الشخص من كامبريدج ، أو على الأقل من إنجلترا ، مع إعطاء العلامة المائية على الورق. لقد أخطأت في افتراض فرضية أن عام 1936 أو نحو ذلك كان الوقت المناسب لكتابة هذا. فمن كان يعلم في ذلك الوقت ومع من قام تورينج بالتواصل؟ . ( 13 , 1930 1936 .)

. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).

1937 - , , . ( , - ).

, ( ) , . ( , 1948 Turbochamp — , , ).

? LinkedIn, , , Microsoft. , , . ( ):



, ( f . .)

? , . « », , . ( , , , , , ).

— , .

«»

, . , , , , , .

, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .

? - (, , , 2005 , «»). , « ».

- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .

. , , , « ». , , , , 1954 , . , , .

, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).

, , , , , 12 , -, , , 21 ).

, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .

, , ? , , . :



, . , , , , , .

: ? , , , .

- , — 1940 — . , 1944 , , . , , .

, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)

, , . . , « » (. . -), -.

. 1969 , , , , , .
, , . . — — . . - , , .

1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).

, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .

, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .

? , , () , . ( , .) , 1 . , .

, , . : « ! » , . . , -, , , .

, , , , , . , : . ; .

, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.

, - , , , . , , , , , , . , , — , , …

: ( ), ( ) ( ).

Wolfram Language?
.
التسجيل للدورات الجديدة . بالطبع استعداد على الانترنت .
Wolfram Language.