🍹 🙎🏼 🌪️ حل معادلة الانحدار الخطي البسيط 👎🏽 ♈️ ⚫️

تتناول هذه المقالة عدة طرق لتحديد المعادلة الرياضية لخط انحدار بسيط (زوجي).

تعتمد جميع طرق حل المعادلة التي تمت مناقشتها هنا على طريقة المربعات الصغرى. نشير إلى الطرق كما يلي:

الحل التحليلي
نزول التدرج
مؤشر ستوكاستيك النسب التدرج

لكل طريقة من طرق حل معادلة الخط المستقيم ، تصف المقالة العديد من الوظائف التي تنقسم أساسًا إلى تلك المكتوبة دون استخدام مكتبة NumPy وتلك التي تستخدم NumPy لإجراء العمليات الحسابية. يُعتقد أن الاستخدام الماهر لـ NumPy يقلل تكاليف الحوسبة.

كل الشفرة في هذه المقالة مكتوبة في بيثون 2.7 باستخدام Jupyter Notebook . شفرة المصدر ونموذج ملف البيانات المنشور على جيثب

تركز المقالة بشكل أكبر على كل من المبتدئين وأولئك الذين بدأوا بالفعل قليلاً في إتقان دراسة قسم واسع جدًا في الذكاء الاصطناعي - التعلم الآلي.

لتوضيح المواد ، نستخدم مثال بسيط للغاية.

مثال الظروف

لدينا خمس قيم تميز اعتماد Y على X (الجدول رقم 1):

الجدول رقم 1 "شروط المثال"

نحن نفترض أن القيم

$x_i$ هو شهر السنة ، و

$y_i$ - الإيرادات هذا الشهر. بمعنى آخر ، تعتمد الإيرادات على شهر السنة و

$x_i$ - العلامة الوحيدة التي تعتمد عليها الإيرادات.مثال على ذلك ، سواء من حيث الاعتماد المشروط للإيرادات على شهر العام ، ومن حيث عدد القيم - هناك عدد قليل للغاية منها. ومع ذلك ، فإن مثل هذا التبسيط سوف يسمح لما يسمى بالأصابع بأن يشرح ، وليس دائما بسهولة ، المواد التي يمتصها المبتدئين. وأيضًا ، ستسمح بساطة الأرقام لأولئك الذين يرغبون في حل المثال على الورق ، دون تكاليف العمالة الكبيرة.افترض أن التبعية المقدمة في المثال يمكن تقريبها جيدًا بالمعادلة الرياضية لخط انحدار بسيط (زوجي) من النموذج:

$Y = a + bx$ حيث

$x$ - هذا هو الشهر الذي تم فيه تلقي الإيرادات ،

$Y$ - الإيرادات المقابلة لهذا الشهر ،

د و ل ا

$دولا$ و

ب

$ب$ - معاملات الانحدار للخط المقدر.لاحظ أن معامل

ب

$ب$ غالبًا ما يسمى الميل أو التدرج للخط المقدر ؛ يمثل المبلغ الذي يجب تغييره

$Y$ عند التغيير

$x$ .من الواضح أن مهمتنا في المثال هي اختيار مثل هذه المعاملات في المعادلة

د و ل ا

$دولا$ و

ب

$ب$ التي الانحرافات من إيراداتنا الشهرية المقدرة من الإجابات الحقيقية ، أي القيم المعروضة في العينة ستكون ضئيلة.

طريقة المربعات الصغرى

وفقًا لطريقة المربعات الصغرى ، يجب حساب الانحراف بتربيعه. هذه التقنية تتجنب السداد المتبادل للانحرافات ، إذا كانت لديهم علامات عكسية. على سبيل المثال ، إذا كان الانحراف في إحدى الحالات هو +5 (زائد خمسة) ، وفي الحالة الأخرى -5 (ناقص خمسة) ، فسيتم تعويض مجموع الانحرافات بشكل متبادل وسيكون 0 (صفر). لا يمكنك تبديد الانحراف ، ولكن استخدام خاصية الوحدة وبعد ذلك ستكون كل الانحرافات إيجابية وتتراكم فينا. لن نتطرق إلى هذه النقطة بالتفصيل ، ولكن لنشير ببساطة إلى أنه من أجل تسهيل العمليات الحسابية ، من المعتاد تحديد الانحراف.هذه هي الطريقة التي تبدو بها الصيغة التي نحدد بها أصغر مجموعة من الانحرافات التربيعية (الأخطاء):

د ق ي ق ة

$ERR (x) = \ sum \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ sum \ limit_ {i = 1} ^ n (f (x_i) -y_i) ^ 2 \ rightarrow دقيقة$ حيث

$f (x_i) = a + bx_i$ هي وظيفة تقريب الإجابات الحقيقية (مثل الإيرادات التي نحسبها) ،

$y_i$ - هذه إجابات حقيقية (الإيرادات الواردة في العينة) ،

$i$ هو مؤشر العينة (عدد الشهر الذي يتم فيه تحديد الانحراف)نحن نفرق بين الوظيفة ونحدد المعادلات التفاضلية الجزئية ، ونحن مستعدون للمضي قدماً إلى الحل التحليلي. لكن أولاً ، دعنا نتعرف على ماهية التمايز ونذكر المعنى الهندسي للمشتق.

التفاضل

التمايز هو عملية إيجاد مشتق للدالة.ما هو مشتق ل؟ يميز مشتق دالة معدل تغيير دالة ويشير إلى اتجاهها. إذا كان المشتق في نقطة معينة موجبًا ، فستزيد الوظيفة ، وإلا تنخفض الوظيفة. وكلما كانت قيمة معامل المشتق أكبر ، كلما ارتفع معدل تغيير قيم الوظيفة ، وكذلك زاوية انحدار الرسم البياني للدالة.على سبيل المثال ، في ظل ظروف نظام الإحداثيات الديكارتية ، فإن قيمة المشتق عند النقطة M (0،0) مساوية لـ +25 تعني أنه عند نقطة معينة ، عند إزاحة القيمة

$x$ الحق في وحدة التعسفي ، والقيمة

$ذ$ يزيد بنسبة 25 وحدة التقليدية. على الرسم البياني ، يبدو وكأنه زاوية ارتفاع حاد إلى حد ما

$ذ$ من نقطة معينة.مثال آخر القيمة المشتقة من -0.1 تعني أنه عند الإزاحة

$x$ لكل وحدة التقليدية ، القيمة

$ذ$ يقلل بنسبة 0.1 وحدة التقليدية فقط. في نفس الوقت ، على الرسم البياني للوظائف ، يمكننا ملاحظة إمالة بالكاد ملحوظة إلى أسفل. من خلال التشبيه مع الجبل ، يبدو أننا ننزلق ببطء المنحدر اللطيف من الجبل ، على عكس المثال السابق ، حيث كان علينا أن نأخذ قمم شديدة الانحدار :)وهكذا ، بعد التمييز بين الوظيفة

$ERR (x) = \ sum \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ بواسطة المعاملات

$دولا$ و

$ب$ ، نحدد معادلات المشتقات الجزئية من الدرجة الأولى. بعد تحديد المعادلات ، نحصل على نظام من معادلتين ، نقرر أيهما يمكن اختيار مثل هذه القيم للمعاملات

$دولا$ و

$ب$ حيث تتغير قيم المشتقات المقابلة في نقاط معينة بقيمة صغيرة جدًا ، وفي حالة الحل التحليلي لا تتغير على الإطلاق. بمعنى آخر ، تصل دالة الخطأ في المعاملات التي تم العثور عليها إلى الحد الأدنى ، حيث تكون قيم المشتقات الجزئية في هذه النقاط صفراً.لذلك ، وفقًا لقواعد التمييز ، معادلة المشتق الجزئي من الرتبة الأولى فيما يتعلق بالمعامل

$دولا$ سوف تأخذ النموذج:

$2na + 2b \ sum \ limit_ {i = 1} ^ nx_i - 2 \ sum \ limit_ {i = 1} ^ ny_i = 2 (na + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i)$ 1st ترتيب معادلة مشتق جزئي فيما يتعلق

$ب$ سوف تأخذ النموذج:

$2a \ sum \ limit_ {i = 1} ^ nx_i + 2b \ sum \ limit_ {i = 1} ^ nx ^ 2_i - 2 \ sum \ limit_ {i = 1} ^ nx_iy_i = 2 \ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i)$ نتيجة لذلك ، حصلنا على نظام من المعادلات يحتوي على حل تحليلي بسيط إلى حد ما:\ تبدأ {المعادلة *}\ تبدأ {الحالات}na + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i = 0\\\ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i) = 0\ end {cases}\ end {equation *}قبل حل المعادلة ، التحميل المسبق ، تحقق من التحميل الصحيح وتنسيق البيانات.

تحميل وتنسيق البيانات

تجدر الإشارة إلى أنه نظرًا لحقيقة أنه بالنسبة للحل التحليلي ، ولاحقًا فيما يتعلق بتدرج الانحدار والتدرج العشوائي ، سنستخدم الكود في صيغتين مختلفتين: باستخدام مكتبة NumPy وبدون استخدامها ، سنحتاج إلى تنسيق البيانات وفقًا لذلك (انظر كود).

تحميل ومعالجة رمز البيانات

#      import pandas as pd import numpy as np import matplotlib.pyplot as plt import math import pylab as pl import random #    Jupyter %matplotlib inline #    from pylab import rcParams rcParams['figure.figsize'] = 12, 6 #   Anaconda import warnings warnings.simplefilter('ignore') #   table_zero = pd.read_csv('data_example.txt', header=0, sep='\t') #         print table_zero.info() print '********************************************' print table_zero print '********************************************' #     NumPy x_us = [] [x_us.append(float(i)) for i in table_zero['x']] print x_us print type(x_us) print '********************************************' y_us = [] [y_us.append(float(i)) for i in table_zero['y']] print y_us print type(y_us) print '********************************************' #     NumPy x_np = table_zero[['x']].values print x_np print type(x_np) print x_np.shape print '********************************************' y_np = table_zero[['y']].values print y_np print type(y_np) print y_np.shape print '********************************************'

تصور

الآن ، بعد أن قمنا أولاً بتنزيل البيانات ، وثانياً ، قمنا بفحص التحميل الصحيح وتنسيق البيانات في النهاية ، سنقوم بإجراء التصور الأول. في كثير من الأحيان ، يتم استخدام طريقة الزوج المزدوج لمكتبة Seaborn لهذا الغرض. في مثالنا ، نظرًا للأعداد المحدودة ، لا معنى لاستخدام مكتبة Seaborn . سوف نستخدم مكتبة Matplotlib العادية وننظر فقط إلى scatterplot.

كود Scatterplot

 print ' №1 "    "' plt.plot(x_us,y_us,'o',color='green',markersize=16) plt.xlabel('$Months$', size=16) plt.ylabel('$Sales$', size=16) plt.show()

الجدول رقم 1 "اعتماد الإيرادات على شهر السنة"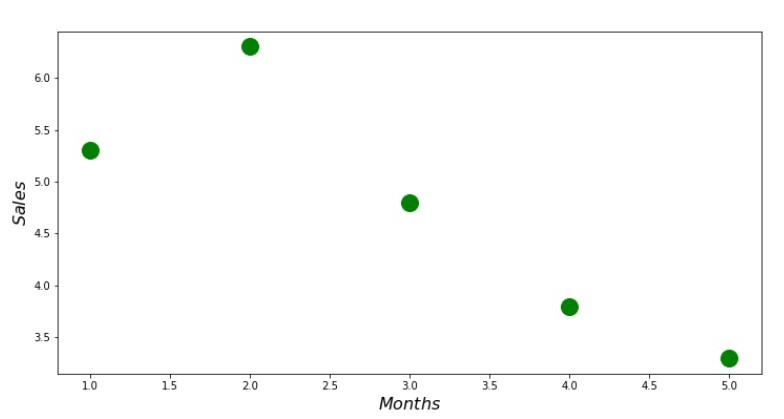

الحل التحليلي

سوف نستخدم الأدوات الأكثر شيوعًا في الثعبان وحل نظام المعادلات:\ تبدأ {المعادلة *}\ تبدأ {الحالات}na + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i = 0\\\ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i) = 0\ end {cases}\ end {equation *}وفقًا لقاعدة Cramer ، نجد محددًا مشتركًا ، وكذلك محددات من قِبل

$دولا$ وبواسطة

$ب$ وبعدها قسمة المحدد على

$دولا$ على المحدد المشترك - نجد المعامل

$دولا$ ، بالمثل ، أوجد المعامل

$ب$ .

رمز الحل التحليلي

 #      a  b    def Kramer_method (x,y): #   ( ) sx = sum(x) #    (   ) sy = sum(y) #       list_xy = [] [list_xy.append(x[i]*y[i]) for i in range(len(x))] sxy = sum(list_xy) #    list_x_sq = [] [list_x_sq.append(x[i]**2) for i in range(len(x))] sx_sq = sum(list_x_sq) #   n = len(x) #   det = sx_sq*n - sx*sx #   a det_a = sx_sq*sy - sx*sxy #   a a = (det_a / det) #   b det_b = sxy*n - sy*sx #   b b = (det_b / det) #   () check1 = (n*b + a*sx - sy) check2 = (b*sx + a*sx_sq - sxy) return [round(a,4), round(b,4)] #       ab_us = Kramer_method(x_us,y_us) a_us = ab_us[0] b_us = ab_us[1] print '\033[1m' + '\033[4m' + "   a  b:" + '\033[0m' print 'a =', a_us print 'b =', b_us print #        def errors_sq_Kramer_method(answers,x,y): list_errors_sq = [] for i in range(len(x)): err = (answers[0] + answers[1]*x[i] - y[i])**2 list_errors_sq.append(err) return sum(list_errors_sq) #       error_sq = errors_sq_Kramer_method(ab_us,x_us,y_us) print '\033[1m' + '\033[4m' + "  " + '\033[0m' print error_sq print #    # print '\033[1m' + '\033[4m' + "     :" + '\033[0m' # % timeit error_sq = errors_sq_Kramer_method(ab,x_us,y_us)

إليك ما حصلنا عليه:

لذلك ، تم العثور على قيم معامل ، يتم تعيين مجموع الانحرافات التربيعية. نرسم خطًا مستقيمًا على الرسم البياني المبعثر وفقًا للمعاملات الموجودة.

رمز خط الانحدار

 #         def sales_count(ab,x,y): line_answers = [] [line_answers.append(ab[0]+ab[1]*x[i]) for i in range(len(x))] return line_answers #   print '№2 "   "' plt.plot(x_us,y_us,'o',color='green',markersize=16, label = '$True$ $answers$') plt.plot(x_us, sales_count(ab_us,x_us,y_us), color='red',lw=4, label='$Function: a + bx,$ $where$ $a='+str(round(ab_us[0],2))+',$ $b='+str(round(ab_us[1],2))+'$') plt.xlabel('$Months$', size=16) plt.ylabel('$Sales$', size=16) plt.legend(loc=1, prop={'size': 16}) plt.show()

الجدول رقم 2 "الإجابات الصحيحة والمقدرة"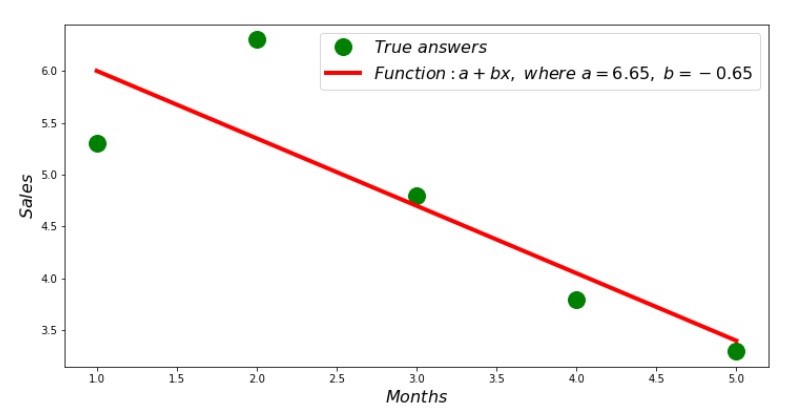

يمكنك إلقاء نظرة على جدول الانحراف لكل شهر. في حالتنا ، لا يمكننا إخراج أي قيمة عملية كبيرة منها ، ولكننا سنرضي فضول مدى جودة معادلة الانحدار الخطي البسيطة التي تميز اعتماد الإيرادات على شهر العام.

كود جدول الانحراف

 #         def error_per_month(ab,x,y): sales_c = sales_count(ab,x,y) errors_percent = [] for i in range(len(x)): errors_percent.append(100*(sales_c[i]-y[i])/y[i]) return errors_percent #   print '№3 " -, %"' plt.gca().bar(x_us, error_per_month(ab_us,x_us,y_us), color='brown') plt.xlabel('Months', size=16) plt.ylabel('Calculation error, %', size=16) plt.show()

الجدول رقم 3 "الانحرافات ، ٪"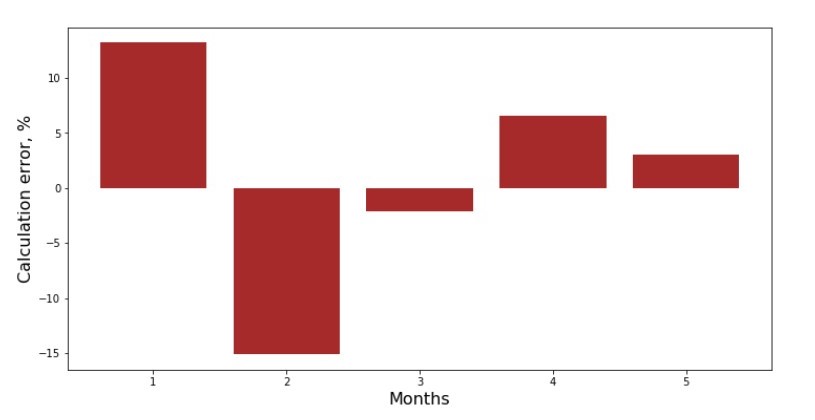

ليست مثالية ، ولكن أكملنا مهمتنا.نكتب وظيفة ، لتحديد المعاملات

$دولا$ و

$ب$ يستخدم مكتبة NumPy ، بشكل أكثر دقة ، سنكتب وظيفتين: واحدة تستخدم مصفوفة عكسية مزيفة (غير مستحسن في الممارسة ، لأن العملية معقدة حسابياً وغير مستقرة) ، والآخر يستخدم معادلة مصفوفة.

رمز الحل التحليلي (NumPy)

 #          1. #     ,      a vector_1 = np.ones((x_np.shape[0],1)) x_np = table_zero[['x']].values #         x_np x_np = np.hstack((vector_1,x_np)) #  ,     print vector_1[0:3] print x_np[0:3] print '***************************************' print #  ,     a  b     def pseudoinverse_matrix(X, y): #      X = np.matrix(X) #    XT = XT #    XTX = XT*X #    inv = np.linalg.pinv(XTX) #      y = np.matrix(y) #    return (inv*XT)*y #   ab_np = pseudoinverse_matrix(x_np, y_np) print ab_np print '***************************************' print #  ,       def matrix_equation(X,y): a = np.dot(XT, X) b = np.dot(XT, y) return np.linalg.solve(a, b) #   ab_np = matrix_equation(x_np,y_np) print ab_np

قارن الوقت المستغرق لتحديد المعاملات

$دولا$ و

$ب$ ، وفقا للأساليب 3 المقدمة.

رمز لحساب وقت الحساب

 print '\033[1m' + '\033[4m' + "       NumPy:" + '\033[0m' % timeit ab_us = Kramer_method(x_us,y_us) print '***************************************' print print '\033[1m' + '\033[4m' + "       :" + '\033[0m' %timeit ab_np = pseudoinverse_matrix(x_np, y_np) print '***************************************' print print '\033[1m' + '\033[4m' + "       :" + '\033[0m' %timeit ab_np = matrix_equation(x_np, y_np)

على مقدار صغير من البيانات ، تأتي وظيفة "مكتوبة ذاتيا" إلى الأمام وتجد المعاملات باستخدام طريقة Cramer.يمكنك الآن الانتقال إلى طرق أخرى للعثور على المعاملات

$دولا$ و

$ب$ .

نزول التدرج

أولاً ، دعونا نحدد ما هو التدرج اللوني. بطريقة بسيطة ، التدرج اللوني عبارة عن قطعة تشير إلى اتجاه الحد الأقصى لنمو الوظيفة. وقياسًا على صعود تسلق ، حيث يبدو التدرج ، يوجد أعلى صعود إلى قمة الجبل. عند تطوير مثال الجبل ، نذكر أننا في الواقع نحتاج إلى أقصى النسب من أجل الوصول إلى الأراضي المنخفضة في أسرع وقت ممكن ، أي الحد الأدنى - المكان الذي لا تزيد فيه الوظيفة أو تقل. في هذه المرحلة ، سيكون المشتق صفراً. لذلك ، لا نحتاج إلى تدرج ، ولكننا بحاجة إلى تدرج. للعثور على التدرج اللوني ، تحتاج فقط إلى ضرب التدرج اللوني -1 (ناقص واحد).نسترعي الانتباه إلى حقيقة أن الوظيفة يمكن أن يكون لها عدة حدود ، وبعد أن انحدرت إلى واحدة منها وفقًا للخوارزمية المقترحة أدناه ، لن نتمكن من العثور على حد أدنى آخر ربما أقل من تلك الموجودة. الاسترخاء ، نحن لسنا في خطر! في حالتنا ، نحن نتعامل مع حد أدنى واحد ، منذ وظيفتنا

$\ sum \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ على الرسم البياني هو المكافئ العادي. وكما ينبغي لنا جميعًا أن نعرف جيدًا من مادة الرياضيات في المدرسة ، فإن المكافئ لديه حد أدنى واحد فقط.بعد أن اكتشفنا سبب احتياجنا إلى التدرج اللوني ، وكذلك أن التدرج اللوني عبارة عن شريحة ، أي متجه بإحداثيات معينة ، والتي هي بالضبط نفس المعاملات

$دولا$ و

$ب$ يمكننا تنفيذ النسب التدرج.قبل البدء ، أقترح قراءة بضع جمل حول خوارزمية النسب:

نحدد إحداثيات المعاملات بطريقة عشوائية زائفة $دولا$ و $ب$ . في مثالنا ، سنحدد المعاملات بالقرب من الصفر. هذه ممارسة شائعة ، ولكن قد يكون لكل ممارسة ممارسة خاصة بها.
من التنسيق $دولا$ اطرح قيمة المشتق الجزئي للترتيب الأول عند هذه النقطة $دولا$ . لذلك ، إذا كان المشتق موجبًا ، فإن الوظيفة تزداد. لذلك ، إذا أخذنا قيمة المشتق ، سنتحرك في الاتجاه المعاكس للنمو ، أي في اتجاه الهبوط. إذا كانت المشتقة سالبة ، فإن الوظيفة في هذه المرحلة تتناقص وتقلل من قيمة المشتق الذي نتحرك باتجاه الهبوط.
نقوم بتنفيذ عملية مماثلة مع التنسيق $ب$ : اطرح قيمة المشتق الجزئي عند النقطة $ب$ .
حتى لا تقفز إلى الحد الأدنى ولا تطير إلى الفضاء البعيد ، من الضروري ضبط حجم الخطوة نحو الهبوط. بشكل عام ، يمكنك كتابة مقال كامل حول كيفية ضبط الخطوة بشكل صحيح وكيفية تغييرها أثناء الهبوط لتقليل تكلفة العمليات الحسابية. لكن لدينا الآن مهمة مختلفة قليلاً ، وسنحدد حجم الخطوة بالطريقة العلمية المتمثلة في "التفاهة" أو ، كما يقولون في عامة الناس ، بشكل تجريبي.
بعد أن نكون من الإحداثيات المعطاة $دولا$ و $ب$ طرح قيم المشتقات ، نحصل على إحداثيات جديدة $دولا$ و $ب$ . نأخذ الخطوة التالية (الطرح) ، بالفعل من الإحداثيات المحسوبة. وهكذا تبدأ الدورة مرارًا وتكرارًا ، حتى يتحقق التقارب المطلوب.

هذا كل شئ! الآن نحن مستعدون للبحث عن أعمق ممر لخندق ماريانا. النزول.

التدرج كود النزول

 #        NumPy. #       x,y,   ( =0,1),  (tolerance) def gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001): #   ( ) sx = sum(x_us) #    (   ) sy = sum(y_us) #       list_xy = [] [list_xy.append(x_us[i]*y_us[i]) for i in range(len(x_us))] sxy = sum(list_xy) #    list_x_sq = [] [list_x_sq.append(x_us[i]**2) for i in range(len(x_us))] sx_sq = sum(list_x_sq) #   num = len(x_us) #   ,    a = float(random.uniform(-0.5, 0.5)) b = float(random.uniform(-0.5, 0.5)) #    ,     1  0 #       errors = [1,0] #    #     ,        ,    tolerance while abs(errors[-1]-errors[-2]) > tolerance: a_step = a - l*(num*a + b*sx - sy)/num b_step = b - l*(a*sx + b*sx_sq - sxy)/num a = a_step b = b_step ab = [a,b] errors.append(errors_sq_Kramer_method(ab,x_us,y_us)) return (ab),(errors[2:]) #    list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_gradient_descence[0][0],3) print 'b =', round(list_parametres_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "    :" + '\033[0m' print len(list_parametres_gradient_descence[1]) print

لقد هبطنا إلى أسفل خندق ماريانا وهناك وجدنا نفس القيم للمعاملات

$دولا$ و

$ب$ ، والذي كان في الواقع متوقعا.لنقم بالغوص مرة أخرى ، فقط هذه المرة ، سيكون ملء سيارتنا في أعماق البحار تقنيات أخرى ، وهي مكتبة NumPy .

كود التدرج الهبوطي (NumPy)

 #           NumPy, #          NumPy def error_square_numpy(ab,x_np,y_np): y_pred = np.dot(x_np,ab) error = y_pred - y_np return sum((error)**2) #        NumPy. #       x,y,   ( =0,1),  (tolerance) def gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001): #   ( ) sx = float(sum(x_np[:,1])) #    (   ) sy = float(sum(y_np)) #       sxy = x_np*y_np sxy = float(sum(sxy[:,1])) #    sx_sq = float(sum(x_np[:,1]**2)) #   num = float(x_np.shape[0]) #   ,    a = float(random.uniform(-0.5, 0.5)) b = float(random.uniform(-0.5, 0.5)) #    ,     1  0 #       errors = [1,0] #    #     ,        ,    tolerance while abs(errors[-1]-errors[-2]) > tolerance: a_step = a - l*(num*a + b*sx - sy)/num b_step = b - l*(a*sx + b*sx_sq - sxy)/num a = a_step b = b_step ab = np.array([[a],[b]]) errors.append(error_square_numpy(ab,x_np,y_np)) return (ab),(errors[2:]) #    list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_gradient_descence[0][0],3) print 'b =', round(list_parametres_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "    :" + '\033[0m' print len(list_parametres_gradient_descence[1]) print

قيم معامل

$دولا$ و

$ب$ دون تغيير.دعونا نلقي نظرة على كيفية تغير الخطأ أثناء هبوط التدرج ، أي كيف تغير مجموع الانحرافات التربيعية مع كل خطوة.

رمز الرسم البياني لمبالغ الانحرافات التربيعية

 print '№4 "   -"' plt.plot(range(len(list_parametres_gradient_descence[1])), list_parametres_gradient_descence[1], color='red', lw=3) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

الرسم البياني №4 "مجموع مربعات الانحرافات في هبوط التدرج"

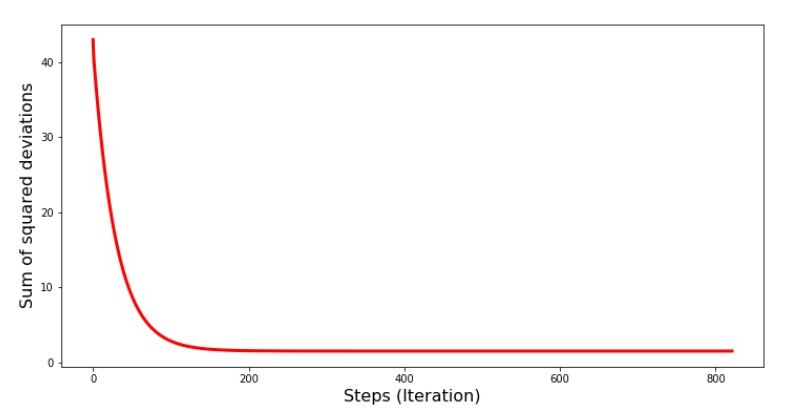
على الرسم البياني ، نرى أنه مع كل خطوة ينخفض الخطأ ، وبعد عدد معين من التكرارات نلاحظ خطًا أفقيًا عمليًا.أخيرًا ، نقدر الفرق في وقت تنفيذ الكود:

رمز لتحديد وقت حساب تدرج النسب

 print '\033[1m' + '\033[4m' + "       NumPy:" + '\033[0m' %timeit list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001) print '***************************************' print print '\033[1m' + '\033[4m' + "       NumPy:" + '\033[0m' %timeit list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001)

ربما نرتكب خطأً ، لكن مرة أخرى ، تكون وظيفة "مكتوبة ذاتياً" بسيطة لا تستخدم مكتبة NumPy قبل استخدام الدالة باستخدام مكتبة NumPy .لكننا لا نقف مكتوفي الأيدي ، بل نتحرك نحو دراسة طريقة أخرى مثيرة لحل معادلة الانحدار الخطي البسيط. قابلني!

مؤشر ستوكاستيك النسب التدرج

من أجل فهم مبدأ تشغيل نزول التدرج العشوائي بسرعة ، من الأفضل تحديد اختلافاته عن نزول التدرج العادي. نحن ، في حالة نزول التدرج ، في معادلات مشتقات

$دولا$ و

$دولا$ استخدم مجاميع قيم جميع السمات والإجابات الحقيقية المتاحة في العينة (أي مجاميع الكل

$x_i$ و

$y_i$ ). في نزول الانحدار العشوائي ، لن نستخدم جميع القيم المتاحة في العينة ، ولكن بدلاً من ذلك ، بطريقة عشوائية زائفة ، سنختار مؤشر عينة يسمى ونستخدم قيمه.على سبيل المثال ، إذا تم تحديد الفهرس بالرقم 3 (ثلاثة) ، فإننا نأخذ القيم

$x_3 = 3 دولا$ و

$y_3 = 4.8 دولا$ ثم نستبدل القيم في معادلات المشتقات ونحدد الإحداثيات الجديدة. بعد ذلك ، وبعد تحديد الإحداثيات ، نقوم مرة أخرى بتحديد مؤشر العينة بشكل عشوائي ، ونستبدل القيم المقابلة للمؤشر في المعادلات التفاضلية الجزئية ، ونحدد الإحداثيات بطريقة جديدة

$دولا$ و

$دولا$ إلخ قبل التقارب ~~تخضير~~ . للوهلة الأولى ، قد يبدو أن هذا يمكن أن ينجح ، لكنه يعمل. صحيح ، تجدر الإشارة إلى أنه ليس كل خطوة تقلل من الخطأ ، ولكن الاتجاه موجود بالتأكيد.ما هي مزايا النسب التدرج العشوائي أكثر من المعتاد؟ إذا كان حجم العينة كبيرًا جدًا ويقاس بعشرات الآلاف من القيم ، فسيكون من الأسهل بكثير معالجتها ، قل ألفًا عشوائيًا من العينة بأكملها. في هذه الحالة ، يتم إطلاق النسب الانحداري العشوائي. في حالتنا ، بالطبع ، لن نلاحظ فرقًا كبيرًا.نحن ننظر إلى الرمز.

رمز لانحدار الانحدار العشوائي

 #   .. def stoch_grad_step_usual(vector_init, x_us, ind, y_us, l): #   ,      ind # (.- stoch_grad_descent_usual) x = x_us[ind] #   y (),     x y_pred = vector_init[0] + vector_init[1]*x_us[ind] #         error = y_pred - y_us[ind] #     ab grad_a = error #    ab grad_b = x_us[ind]*error #     vector_new = [vector_init[0]-l*grad_a, vector_init[1]-l*grad_b] return vector_new #   .. def stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800): #          vector_init = [float(random.uniform(-0.5, 0.5)), float(random.uniform(-0.5, 0.5))] errors = [] #    #       (steps) for i in range(steps): ind = random.choice(range(len(x_us))) new_vector = stoch_grad_step_usual(vector_init, x_us, ind, y_us, l) vector_init = new_vector errors.append(errors_sq_Kramer_method(vector_init,x_us,y_us)) return (vector_init),(errors) #    list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3) print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_stoch_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "     :" + '\033[0m' print len(list_parametres_stoch_gradient_descence[1])

نحن ننظر بعناية إلى المعاملات ونلتقط على السؤال "كيف ذلك؟". حصلنا على قيم أخرى للمعاملات

$دولا$ و

$ب$ . ربما وجد نزول الانحدار العشوائي عوامل أكثر مثالية للمعادلة؟ للأسف ، لا. يكفي أن نلقي نظرة على مجموع الانحرافات التربيعية ونرى أنه مع القيم الجديدة للمعاملات ، يكون الخطأ أكبر. لا تتسرع في اليأس. نحن نخطط لتغيير الخطأ.

رمز الرسم البياني لمجموع الانحرافات التربيعية في النسب التدرج العشوائي

 print ' №5 "   -"' plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

الرسم البياني №5 "مجموع مربعات الانحرافات في هبوط التدرج العشوائي"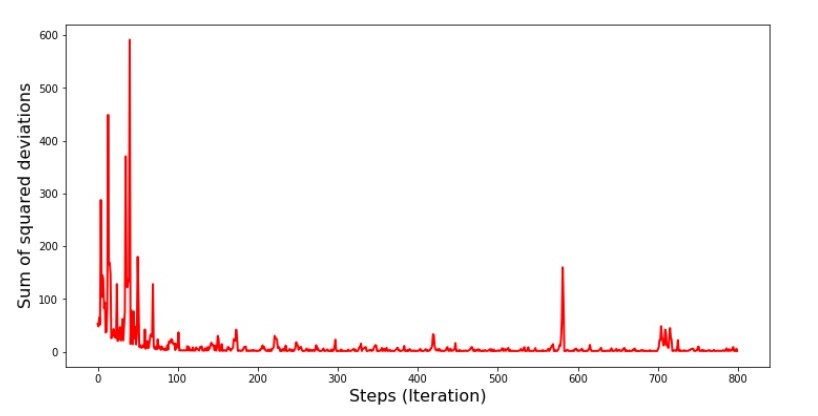

بعد الاطلاع على الجدول الزمني ، كل شيء يقع في مكانه ، والآن سنصلح كل شيء.إذن ماذا حدث؟ حدث ما يلي.عندما نختار شهرًا بشكل عشوائي ، فهذا الشهر المحدد هو الخوارزمية التي تسعى إلى تقليل الخطأ في حساب الإيرادات. ثم نختار شهرًا آخر ونكرر العملية الحسابية ، لكننا نخفف الخطأ بالفعل للشهر الثاني المحدد. والآن ، دعونا نتذكر أنه خلال الشهرين الأولين ، انحرفنا بشكل كبير عن خط معادلة الانحدار الخطي البسيط. هذا يعني أنه عند تحديد أي من هذين الشهرين ، ثم تقليل خطأ كل منهم ، فإن الخوارزمية تزيد الخطأ بشكل خطير خلال العينة. ماذا تفعل؟ الجواب بسيط: تحتاج إلى تقليل خطوة النزول. بعد كل شيء ، من خلال تقليل خطوة الهبوط ، فإن الخطأ سوف يتوقف أيضًا عن "القفز" لأعلى ولأسفل. بدلاً من ذلك ، لن يتوقف الخطأ "تخطي" ، لكنه لن يفعل ذلك بسرعة :) سنتحقق منه.

رمز لتشغيل SGD في خطوات أقل

 #  ,    100       list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3) print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_stoch_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "     :" + '\033[0m' print len(list_parametres_stoch_gradient_descence[1]) print ' №6 "   -"' plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

الرسم البياني رقم 6 "مجموع مربعات الانحرافات في نزول الانحدار العشوائي (80 ألف خطوة)"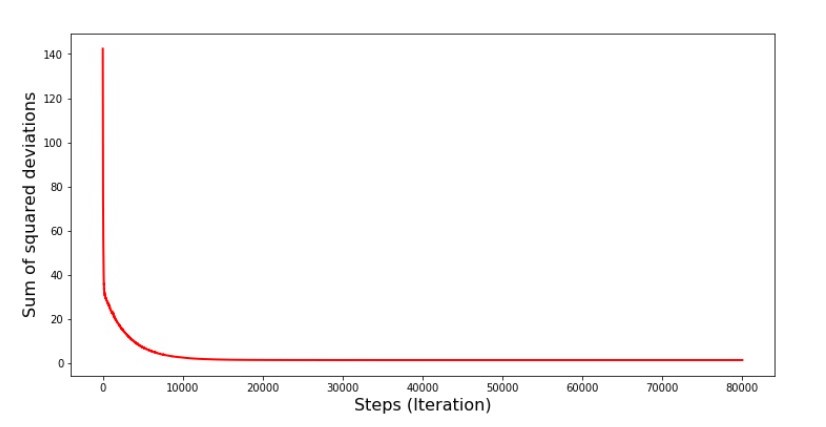

تحسنت قيم المعاملات ، لكنها ما زالت غير مثالية. نظريا ، هذا يمكن تصحيحه بهذه الطريقة. على سبيل المثال ، في آخر 1000 تكرار ، نختار قيم المعاملات التي حدث بها الحد الأدنى من الأخطاء. صحيح ، لهذا علينا أن نكتب قيم القيم بأنفسنا. لن نفعل ذلك ، بل ننتبه إلى الجدول. يبدو سلسًا ، ويبدو أن الخطأ يتناقص. هذا في الواقع ليس هو الحال. دعونا نلقي نظرة على التكرار 1000 الأولى ومقارنتها مع آخر.

رمز مخطط SGD (أول 1000 خطوة)

 print ' №7 "   -.  1000 "' plt.plot(range(len(list_parametres_stoch_gradient_descence[1][:1000])), list_parametres_stoch_gradient_descence[1][:1000], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show() print ' №7 "   -.  1000 "' plt.plot(range(len(list_parametres_stoch_gradient_descence[1][-1000:])), list_parametres_stoch_gradient_descence[1][-1000:], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

الجدول رقم 7 "مجموع مربعات انحرافات SGD (الخطوات الأولى 1000)"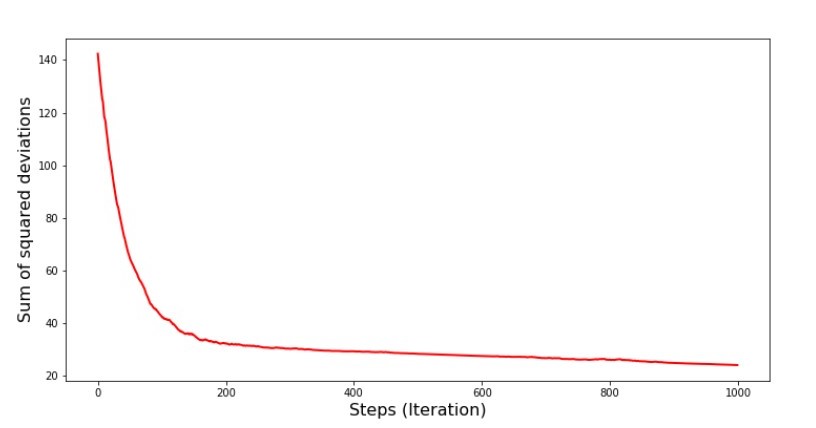

الرسم البياني رقم 8 "مجموع مربعات انحرافات SGD (آخر 1000 خطوة)".

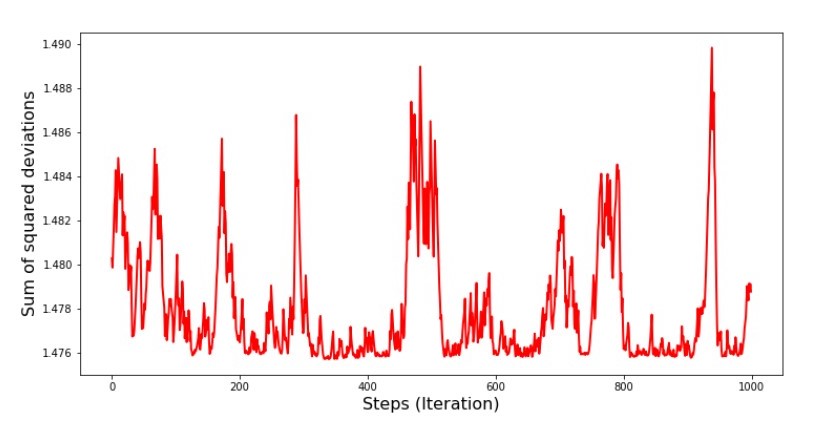في بداية الهبوط ، نلاحظ انخفاضًا موحدًا إلى حد ما في الخطأ. في التكرارات الأخيرة ، نرى أن الخطأ يدور وحول قيمة 1.475 وفي بعض النقاط تساوي هذه القيمة المثلى ، ولكن بعد ذلك ترتفع على أي حال ... مرة أخرى ، يمكنني تدوين قيم المعاملات

$دولا$ و

، ثم حدد تلك التي يكون الحد الأدنى للخطأ فيها. ومع ذلك ، واجهنا مشكلة أكثر خطورة: كان علينا اتخاذ 80 ألف خطوة (انظر الكود) للحصول على قيم قريبة من المستوى الأمثل. وهذا يتناقض بالفعل مع فكرة توفير الوقت الحسابي مع نزول الانحدار العشوائي نسبة إلى التدرج. ما الذي يمكن تصحيحه وتحسينه؟ ليس من الصعب أن نلاحظ أننا في التكرارات الأولى ننزلق بثقة ، وبالتالي ، يجب أن نترك خطوة كبيرة في التكرارات الأولى وأن نخفف هذه الخطوة أثناء تقدمنا للأمام. لن نقوم بذلك في هذه المقالة - لقد استمر بالفعل. أولئك الذين يرغبون في أن يفكروا في كيفية القيام بذلك ، هذا ليس بالأمر الصعب :)الآن سنقوم بإجراء نزول تدرج عشوائي باستخدام مكتبةNumPy

$ب$ (ولن نتعثر على الأحجار التي حددناها سابقًا)

رمز نزول التدرج العشوائي (NumPy)

 #       def stoch_grad_step_numpy(vector_init, X, ind, y, l): x = X[ind] y_pred = np.dot(x,vector_init) err = y_pred - y[ind] grad_a = err grad_b = x[1]*err return vector_init - l*np.array([grad_a, grad_b]) #      def stoch_grad_descent_numpy(X, y, l=0.1, steps = 800): vector_init = np.array([[np.random.randint(X.shape[0])], [np.random.randint(X.shape[0])]]) errors = [] for i in range(steps): ind = np.random.randint(X.shape[0]) new_vector = stoch_grad_step_numpy(vector_init, X, ind, y, l) vector_init = new_vector errors.append(error_square_numpy(vector_init,X,y)) return (vector_init), (errors) #    list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3) print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_stoch_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "     :" + '\033[0m' print len(list_parametres_stoch_gradient_descence[1]) print

تحولت القيم إلى أن تكون هي نفسها تقريبًا أثناء الهبوط دون استخدام NumPy . ومع ذلك ، هذا منطقي.سوف نكتشف مقدار الوقت الذي استغرقهنا هبوط التدرج العشوائي.

رمز لتحديد وقت حساب SGD (80 ألف خطوة)

 print '\033[1m' + '\033[4m' +\ "        NumPy:"\ + '\033[0m' %timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000) print '***************************************' print print '\033[1m' + '\033[4m' +\ "        NumPy:"\ + '\033[0m' %timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000)

كلما اقتربنا من الغابة ، كلما كانت السحب أغمق: مرة أخرى ، تظهر الصيغة "المكتوبة ذاتيا" أفضل نتيجة. كل هذا يشير إلى أنه ينبغي أن يكون هناك طرق أكثر دقة لاستخدام مكتبة NumPy ، والتي تسرع بالفعل عمليات العمليات الحسابية. في هذه المقالة لن نعرف عنها. سيكون هناك شيء للتفكير في وقت فراغك :)

لخص

قبل أن ألخص ، أود أن أجيب على السؤال الذي نشأ على الأرجح عن القارئ العزيز. لماذا ، في الواقع ، مثل هذا "العذاب" ذو النزول ، لماذا يتعين علينا أن نذهب صعوداً ونزولاً في الجبل (لأسفل بشكل أساسي) للعثور على الأراضي المنخفضة العزيزة ، إذا كان لدينا جهاز قوي وبسيط في أيدينا ، في شكل حل تحليلي يبعث بنا على الفور إلى المكان المناسب؟الجواب على هذا السؤال يكمن على السطح. لقد درسنا الآن مثالا بسيطا للغاية فيه الإجابة الصحيحة

يعتمد على ميزة واحدة

$y_i$

$x_i$ .في الحياة ، لا يظهر هذا كثيرًا ، لذا تخيل أن لدينا علامات 2 أو 30 أو 50 أو أكثر. أضف إلى هذا الآلاف ، أو حتى عشرات الآلاف من القيم لكل سمة. في هذه الحالة ، قد لا يجتاز الحل التحليلي الاختبار ويفشل. في المقابل ، فإن الانحدار التدريجي وأشكاله سوف تقرب ببطء ولكن بثبات من الهدف - الحد الأدنى من الوظيفة. ولا تقلق بشأن السرعة - ربما سنحلل أيضًا الطرق التي تسمح لنا بتعيين وضبط طول الخطوة (أي السرعة).والآن في الواقع ملخص موجز.أولاً ، آمل أن تساعد المادة المقدمة في المقالة "علماء التاريخ" المبتدئين في فهم كيفية حل معادلات الانحدار الخطي البسيط (وليس فقط).ثانياً ، درسنا عدة طرق لحل المعادلة. الآن ، اعتمادًا على الموقف ، يمكننا اختيار أفضل الحلول لحل المشكلة.ثالثًا ، رأينا قوة الإعدادات الإضافية ، وهي طول خطوة نزول التدرج. لا يمكن إهمال هذه المعلمة. كما هو مذكور أعلاه ، من أجل تقليل تكلفة العمليات الحسابية ، يجب تغيير طول الخطوة على طول النسب.رابعا ، في حالتنا ، أظهرت الدالات "المكتوبة ذاتيا" أفضل نتيجة زمنية للحسابات. ربما يرجع هذا إلى عدم الاستخدام الأكثر احترافية لقدرات مكتبة NumPy. ولكن أن يكون هذا ما قد يكون ، الاستنتاج هو كما يلي. من ناحية ، في بعض الأحيان يستحق التشكيك في الآراء الراسخة ، ومن ناحية أخرى ، لا يستحق الأمر دائمًا تعقيد الأمور - على العكس ، في بعض الأحيان تكون الطريقة الأكثر بساطة لحل المشكلة أكثر فعالية. وبما أن هدفنا كان تحليل ثلاثة طرق في حل معادلة الانحدار الخطي البسيط ، فإن استخدام الدالات "المكتوبة ذاتيا" كان كافيا بالنسبة لنا.

العمل السابق للمؤلف - "ندرس بيان نظرية الحد المركزي باستخدام التوزيع الأسي"

$\leftarrow$

العمل التالي للمؤلف - "نأتي معادلة الانحدار الخطي في شكل مصفوفة"

$\rightarrow$

الأدب (أو شيء من هذا القبيل)

1. الانحدار الخطي

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. طريقة المربعات الصغرى

mathprofi.ru/metod_naimenshih_kvadratov.html

3. مشتق

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. التدرج

mathprofi.ru /proizvodnaja_po_napravleniju_i_gradient.html

5. Gradient descent

habr.com/en/post/471458

habr.com/en/post/307312

artemarakcheev.com//2017-12-31-31/linear_regression

6. مكتبة

NumPy docs.scipy.org/doc/ numpy-1.10.1 / reference / born / numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2. أتش تي أم أل

حل معادلة الانحدار الخطي البسيط

مثال الظروف

طريقة المربعات الصغرى

التفاضل

تحميل وتنسيق البيانات

تصور

الحل التحليلي

نزول التدرج

مؤشر ستوكاستيك النسب التدرج

لخص

الأدب (أو شيء من هذا القبيل)

More articles: