درسنا طريقة مونت كارلو ، اليوم سنرى كيف يلعب عقل الكمبيوتر عام 2048 باستخدام minimax القديم الجيد مع لقطة ألفا بيتا.

كُتِب المقال بدعم من EDISON ، وهي شركة تطور تطبيقات الهاتف المحمول وتوفر خدمات اختبار البرمجيات .
حل التجسس على المستخدم stackoverflow
 ovolve
ovolve ، الذي لاحظ في المناقشة
كيفية تعليم لعبة 2048 .
ترجمة تعليق من ovolveأنا مؤلف البرنامج المذكور في هذا الموضوع. يمكنك رؤية الذكاء الاصطناعى
أثناء العمل أو رؤية
الكود .
حاليًا ، يفوز البرنامج في حوالي 90٪ من الحالات عن طريق تنفيذ برامج جافا النصية في متصفح على جهاز الكمبيوتر المحمول الخاص بي ، حيث ينفق 100 مللي ثانية على التفكير في الدورة ، وهو يعمل ، وإن لم يكن بشكل مثالي ، ولكن جيد.
نظرًا لأن اللعبة عبارة عن مساحة منفصلة للدولة تحتوي على معلومات كاملة ، وفي الحقيقة أنها لعبة تقوم بدورها مثل لعبة الشطرنج والمدققون ، فقد استخدمت نفس الأساليب التي أظهرت أدائها في هذه الألعاب ، وهي
البحث عن minimax مع
لقطة ألفا بيتا . نظرًا لأن الروابط توفر الكثير من المعلومات حول هذه الخوارزمية ، سأتحدث فقط عن الاستدلالين الرئيسيين اللذين استخدمتهما في
وظيفة التقدير الثابت وإضفاء الطابع الرسمي على العديد من الافتراضات البديهية التي وضعها أشخاص آخرون هنا.

رتابة
يحاول هذا الاستدلال التأكد من أن جميع قيم التجانب إما تزيد أو تنقص من اليسار / اليمين و لأعلى / لأسفل. هذا الكشف عن مجريات الأمور وحده يعكس تخمين أن العديد من الآخرين قد ذكروا أنه يجب تجميع البلاط الأكثر قيمة في الزاوية. هذا ، كقاعدة عامة ، يمنع تراكم البلاط الأقل قيمة ويحافظ على تنظيم اللوحة ، حيث تتالي البلاطات الأصغر حجمًا في بلاطات أكبر.
هنا لقطة للشبكة رتيبة تماما. حصلت على هذا الموقف من خلال تشغيل خوارزمية مع وظيفة eval المثبتة من أجل تجاهل الاستدلال الأخرى وتأخذ في الاعتبار رتابة فقط.

نعومة (نعومة ، متساوية)
يميل مجريات الأمور المذكورة أعلاه في حد ذاتها إلى إنشاء هياكل يتم فيها تقليل قيمة الخلايا المجاورة ، ولكن بالطبع يجب أن يكون لدى الجيران نفس المعنى للجمع. لذلك ، فإن مجريات الأمور الخاصة بالنعومة تقيس ببساطة الفرق في القيم بين البلاط المجاور ، في محاولة لتقليل عددها.
قدم أحد المعلقين في Hacker News
شكلاً مثيرًا للاهتمام لهذه الفكرة من حيث نظرية الرسم البياني.
ترجمة إضفاء الطابع الرسمي مع هاكر نيوزبالأمس ، عرضت هذه اللعبة على زميل ، وهو محب لنظرية الرسم البياني ، وقررنا أيضًا التفكير في كيفية حل هذه اللعبة باستخدام الذكاء الاصطناعي.
أبسط الحلول هو minimax ، والتي ، كما أراها ، يتم تنفيذها بشكل جيد. إذا كان شخص ما هنا غير معتاد على الحد الأدنى ، فقد كتب OP رمزًا أنيقًا جدًا وعلق جيدًا وسيكون تعليميًا رائعًا.
كان النهج الأقل كثافة الحسابية الذي اقترحناه هو نمذجة حالة اللعبة في شكل رسم بياني G (V ، E) ، حيث V عبارة عن مجموعة من البلاط النشط و E عبارة عن مجموعة من الحواف التي تربط البلاط المجاور الموزون حسب الوظيفة c (v1 ، v2) ، والتي تُرجع القيمة المطلقة للفرق بين التجانب. لكل حل ، يختار الذكاء الاصطناعي حركة تقلل من مجموع الأوزان لجميع الحواف في حالة اللعبة الجديدة.
والسبب في ذلك هو أن الطريقة الوحيدة لإحراز تقدم في اللعبة هي الحصول على مربعات لها نفس القيم بجانب بعضها البعض ، والتي سيكون وزنها في G 0. وبالتالي ، يجب أن تحاول منظمة العفو الدولية تقليل الوزن الكلي. في النهاية ، سيكون هناك عدد كبير على الألواح ذات وزن كبير من الحواف للبلاط المجاور ، لذلك ستحاول منظمة العفو الدولية إبقاء هذه البلاطات بجوار البلاط الكبير الآخر لتقليل الفرق.
نظرًا لأن اللعبة عشوائية ، فإن الطريقة التي وصفتها قد لا تعمل في أسوأ الحالات ، ولكن يمكن تطبيقها أيضًا على حل minimax الحالي كدالة للوزن لكل عقدة في الشجرة.
فيما يلي لقطة للشبكة الناعمة تمامًا ، والتي يوفرها هذا
الشوكة الوهمية الممتازة.
(اربط إلى أرشيف الويب ، بينما تعمل البرامج النصية لـ Java على الصفحة ويمكنك استخدام لوحة المفاتيح للقيام بأي خطوة في أي اتجاه - ملاحظة بواسطة المترجم).بلاط فضفاض
وأخيرًا ، هناك عقوبة لوجود عدد قليل جدًا من المربعات المجانية ، نظرًا لأن الخيارات يمكن أن تنتهي بسرعة عندما يصبح ملعب الملعب شديد الضيق.
وهذا كل شيء! البحث في مساحة اللعبة مع تحسين هذه المعايير يعطي أداءً جيدًا بشكل مدهش. أحد فوائد استخدام نهج عام مثل هذا بدلاً من استراتيجية نقل مشفرة بشكل صريح هو أن الخوارزمية يمكنها في كثير من الأحيان إيجاد حلول مثيرة للاهتمام وغير متوقعة. إذا لاحظت تقدمه ، فغالبًا ما يقوم بحركات مدهشة ولكنها فعالة ، مثل التغيير المفاجئ للجدران أو الزوايا ، الذي يقوم ببناء لعبته بالقرب منه.

تغيير صغير
توضح لقطة الشاشة قوة هذا النهج. لقد قمت بإزالة الحد الأقصى للبلاط (بحيث تستمر في النمو بعد الوصول إلى 2048) ، وهنا هي أفضل نتيجة بعد ثمانية اختبارات.
نعم ، هذا 4096 مع 2048. =) هذا يعني أنه قد وصل إلى بلاط 2048 بعيد المنال على لوحة واحدة.
يرد في هذه المقالة رمز Java-Script الخاص بـ minimax مع لقطة alpha-beta والتقييم الثابت من ovolve user stackoverflow.
طريقة minimax مكرسة للعديد من مقالات habr الممتازة ، لذلك نحذف التفسير الأكاديمي المفصل لما تتكون منه. بالنسبة لأولئك الذين
انضموا إلى مجتمع تكنولوجيا المعلومات ، سمعت
مؤخرًا المصطلحات الجميلة "minimax" و "alpha-beta clipping" ، لكن لا أعرف ماذا يعني هذا ، دعونا نحاول حرفيًا في فقرتين ، لشرح المعنى العام.
مينيماكس
في بعض الألعاب ، يمكن تمثيل عملية اللعبة بين لاعبين (الذين يقومون بدورهم بدورهم في التحرك) باعتبارها ما يسمى شجرة الخيارات. في كل موقف محدد ، عادة ما يكون لكل لاعب خيار بين الخيارات المختلفة لحركته. ورداً على كل خيار من هذه الخيارات ، يمكن أن يكون الخصم أيضًا في نواح كثيرة.
جزء من شجرة الخياراتنظرًا لأن هناك في أي لحظة من اللعبة معلومات كاملة عن حالة الملعب ، يمكن دائمًا تقدير الوضع الحالي للموقف بدقة. وتسمى هذه الوظيفة وظيفة
التقييم الثابت أو اختصار
SFO . علاوة على ذلك ، كلما كانت هذه الوظيفة أكثر أهمية عند تقييم موضع معين ، كلما كان الموضع الخاص باللاعب أكثر فائدة (دعنا نسميها
اللاعب المعظم ). كلما كانت القيمة العددية لهذه الوظيفة أصغر عند تقييم الموضع ، كلما كان الموضع الأفضل للاعب الثاني (دعنا نسميها
اللاعب المصغر ).
بعد كل خطوة ، يتغير الموقف ، وبالتالي تتغير درجاته. عند التفكير في مجموعة الخيارات ، لا يحتاج كل لاعب إلى تفضيل تلك الفروع التي يكون التصنيف فيها أكثر ملاءمة له. يجب عليك أيضًا تجنب تلك الفروع التي يكون فيها تقييم الموقف مناسبًا للخصم.
من المفترض أن يسترشد الخصم بالعقلانية ويتجنب أيضًا الخيارات التي قد تؤدي به إلى الخسارة. أي أن كل لاعب ، عند اختيار أحد الخيارات ، ينطلق من زيادة مصلحته إلى الحد الأقصى وفي نفس الوقت تقليل ربح الخصم.
هذا هو الحد الأدنى.
ألفا بيتا لقطة
من الواضح تمامًا: من الذي يحسب شجرة من موقع معين إلى عمق أكبر ، لديه فرص أكبر للفوز. ولكن هناك مصدر إزعاج واحد - تتمتع شجرة الخيارات في الألعاب بعادة سيئة تتمثل في التفوق والنمو بشكل كبير مع كل مستوى من مستويات التعشيش. إن قدرات الفرز للبرامج ، وحتى أكثر من ذلك محدودة ، فإن عد "الحق في حصيرة" أمر بعيد المنال دائمًا. يمكن أن يتحول بسهولة إلى أن اللاعب قد تم احتسابه في موضع يتمتع فيه بتقييم جيد لمجال اللعب ، ولكن حرفيًا في المستوى التالي (غير قابل للقراءة) ، لدى الخصم الفرصة لاتخاذ مثل هذه الخطوة التي تؤدي إلى تغيير جذري في تقدير الموقف إلى عكس ذلك.
على من يقع اللوم وماذا يفعل؟ التعقيد الحسابي هو المسؤول عن اجتياز شجرة كاملة ؛ يقترح القتال عن طريق قطع فروع غير ضرورية. إذا رأى اللاعب الذي يقوم بتقييم الموضع أن بعض فروع شجرة الخيارات:
أو أقل ربحية له من الفروع الأخرى التي تم تحليلها بالفعل ،
أو أكثر فائدة للخصم من الفروع الأخرى التي تم تحليلها بالفعل ،
ثم يتجاهل اللاعب هذا الفرع ، ولا يضيع الوقت والموارد في النظر في الخيارات الفرعية من هذا الفرع الذي من الواضح أنه أسوأ بالنسبة له.
يتيح لك ذلك تخصيص المزيد من موارد الحوسبة لحساب الفروع الأكثر ملاءمة لعمق عرض أكبر في شجرة الخيارات. في عملية تقييم ملعب التشغيل على مستويات مختلفة من شجرة الخيارات ، يعمل المشغل بمعاملين متغيرين ديناميكيًا -
ألفا (قيمة الصندوق الاجتماعي للتنمية التي تتم مواجهتها في أدنى حد ممكن في الفرع - أي أكثر ملاءمة لمشغل التصغير)
وبيتا (قيمة الصندوق الأكثر شيوعًا التي يتم مواجهتها في الفرع - أي أكثر ملاءمة للاعب تعظيم). في كل مستوى ، تتيح لك مقارنة SFD للموضع الحالي بمعاملات
ألفا وبيتا اكتساح (دون حسابها تمامًا) الفروع
الأقل فائدة للاعب الذي يقوم بتقييم الموضع و / أو
أكثر فائدة لخصمه.
هذا هو لقطة ألفا بيتا.
وظيفة minimax العودية مع لقطة ألفا بيتا
يتم تطبيق 2048 مع AI كتطبيق Excel مع وحدات ماكرو VBA ، هكذا تبدو خوارزمية minimax مع لقطة alpha beta كقاعدة مرئية مرئية. Ovolve رمز في جافا سكريبت function AI(grid) { this.grid = grid; }
وظيفة التقييم الثابت
نظرًا لأنه في كل مستوى في شجرة الخيارات يجب عليك تقييم مجال اللعب (من أجل تحديد أي اللاعبين ، يكون الموضع المقدر أكثر فائدة بالفعل) ، تحتاج إلى تحديد المعايير التي تميز الموضع الجيد عن الموضع السيئ.
نحن نفترض أن المشغل الذي تم تعظيمه هو الشخص (أو AI) الذي يقرر أيًا من الاتجاهات الأربعة (أعلى أو يسار أو يمين أو أسفل) لتغيير كل التجانبات. اللاعب المصغر هو الروتين الفرعي الخبيث الذي يولد بشكل عشوائي 2 أو 4 في أكثر الأماكن غير المناسبة.
يتم تجميع SFO من منظور لاعب تعظيم. كلما ارتفع تصنيف الصندوق الاجتماعي للتنمية عن الملعب ، كان الموضع "الحد الأقصى" أفضل. أقل - وأكثر متعة الموقف على لوحة ل "الحد الأدنى".
في حالة 2048 - ما هي العوامل التي تعتبر مواتية للشخص الذي يتحرك؟
رتابة
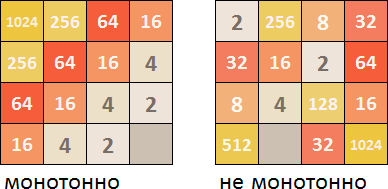
أولاً ، من المستحسن أن يتم ترتيب البلاط في ترتيب تصاعدي / تنازلي في بعض الاتجاهات. إذا لم يتم ذلك ، فعندما يتم إنشاء مربعات جديدة ، فسوف تسد مساحة الملعب سريعًا ببلاطات مرتبة عشوائيًا بأحجام مختلفة ، والتي لا يمكن توصيلها بشكل طبيعي مع بعضها البعض على الفور.
في منطقة سيبيريا الفيدرالية ، تحتاج إلى البحث في جميع الاتجاهات الأربعة (من أعلى إلى أسفل ومن اليسار إلى اليمين ومن اليمين إلى اليسار ومن أسفل إلى أعلى) وحساب الأماكن التي يتزايد فيها التزايد المتناقص أو المتزايد. إذا كان هناك تقدم في بلاطات لا تتناسب مع السلسلة العامة ، فإن هذا يقلل من المعامل العددي للرتابة. بعد ذلك ، من بين 4 معاملات لكل الاتجاهات ، يتم اختيار الأفضل ، ويؤخذ في الاعتبار في القيمة الإجمالية للمنطقة الفيدرالية السيبيرية.
نعومة

علاوة على ذلك ، سيكون من الأفضل لو أن التقدم من الوقوف في صف واحد من البلاط لم يكن في ازدياد فحسب ، بل كان غير متناقص (أو بدلاً من تناقص الصف ، من الأفضل عدم الزيادة) ، أي أنه من الجيد أن تكون القطع نفسها قريبة ، مما يسمح لها بالانهيار في واحدة ، وكسب النقاط و زيادة المساحة الحرة في الملعب.
لذلك ، تبحث منطقة سيبيريا الفيدرالية عن نفس البلاط المجاور في ساحة اللعب وتأخذ في الاعتبار عدد هذه الأزواج في معامل خاص.
خلايا فارغة

من الواضح ، أنه كلما زادت المساحة الحرة ، زادت مساحة المناورة وأقل احتمالًا أن تخسر بسرعة.
يعتبر SFO الخلايا الفارغة في الحقل وأكثر من ذلك ، يعتبر الموضع أكثر ربحية للاعب المكبر.
البلاط الأقصى
نظرًا لأن الشيء الرئيسي في هذه اللعبة هو الحصول على بلاطة كبيرة في الملعب ، كلما كان ذلك أفضل - 2048 ، 4096 ، 8192 (أو أي شيء لديك القوة والصبر عليه) ، يجب اعتبار الخيارات التي تكون فيها قيمة الحد الأقصى للبلاط هي الصندوق الاجتماعي الأكثر ربحية.
منطقة سيبيريا الفيدرالية لعام 2048
تنفيذ منطقة سيبيريا الفيدرالية باعتبارها ماكرو VBA Ovolve رمز في جافا سكريبت function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
يمكن تنزيل تطبيق Excel نفسه
من Google .
ويرد وصف وظيفة التطبيق
في مقال سابق ، حيث يلعب AI باستخدام طريقة مونت كارلو . تمت إضافة حل اليوم إلى Monte Carlo الحالي.
جميع المواد من سلسلة AI و 2048
- مونتي كارلو
- Minimax + ألفا بيتا لقطة
- في انتظار الحد الأقصى
- الشبكة العصبية