TextRadar خوارزمية البحث غامض - النهج الأساسية
على عكس مقارنات السلسلة المشوشة ، عندما تكون كلتا السلاسل المقارنة متكافئة ، يتم إبراز سلسلة البحث وسلسلة البيانات في مهمة البحث المشوشة ، ومن الضروري تحديد درجة عدم تشابه السلسلتين ، ولكن درجة تواجد سلسلة البحث في سلسلة البيانات.
بيان المشكلة
يتم تقديم سلسلة بيانات وسلسلة بحث كمجموعات أحرف عشوائية تتكون من كلمات - مجموعات من الأحرف مفصولة بمسافات.
يجب أن تجد في سطر البيانات مجموعة الأجزاء الأقرب إلى خط البحث من خلال التكوين والموضع النسبي للأحرف.
لتقييم جودة نتيجة البحث ، احسب معامل الملاءمة ، الذي يجب أن تكمن قيمته في النطاق من 0 إلى 1 ، حيث يجب أن تتطابق 0 مع الغياب الكامل لأحرف سطر البحث في سطر البيانات ، ويجب أن يتوافق الرقم 1 مع وجود سطر البحث في سطر البيانات في النموذج غير المشوَّه.
يجب أن يتم البحث عن طريق تحليل حرف-حرف لخطوط المصدر ، مع مراعاة الترتيب المتبادل بين الأحرف والكلمات في السطور ، ولكن دون مراعاة بناء الجملة ومورفولوجيا اللغة.
وصف الخوارزمية
يتم البحث على عدة مراحل.
بناء مصفوفة من الصدف
مصفوفة المطابقة (M) هي مصفوفة ثنائية الأبعاد ، وعدد الأعمدة التي تتوافق مع طول سلسلة البيانات ، وعدد الصفوف إلى طول سلسلة البحث. تأخذ عناصر مصفوفة الصدفة القيم 0 أو 1 حسب ما إذا كانت الأحرف المقابلة للخطوط تتزامن أم لا ، باستثناء المسافات (محددات الكلمات).
مصفوفة المطابقة لسلسلة البيانات "ABCD EF" وسلسلة البحث "ABC" لها النموذج:
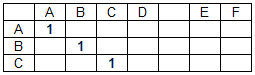
مطابقة عنصر المصفوفة m (i، j) = 1 إذا كانت d (i) = s (j) ، حيث D عبارة عن صفيف من أحرف سلسلة البيانات ، S عبارة عن صفيف من أحرف سلسلة البحث ، أنا رقم عمود لمصفوفة مطابقة M (رقم حرف سلسلة البيانات) ) ، j هو رقم الصف لمصفوفة المطابقة (رقم الحرف في سلسلة البحث). في حالات أخرى ، m (i ، j) = 0. لا تؤخذ مطابقات فواصل الكلمات (في حالتنا ، المسافات) في الاعتبار ، أي: m (i ، j) = 0 إذا كانت d (i) = s (j) = '' .
تطابق مصفوفة الأقطار
عناصر المصفوفة مصادفة M شكل الأقطار. تكون عناصر المصفوفة على نفس القطر إذا كانت مؤشراتها i و j تختلف في وقت واحد عن طريق +1 أو by - 1.

تتوافق الأقطار مع مواضع سلسلة البحث في تسلسل الإزاحات على طول سلسلة البيانات.

يتم تمييز عناصر أحد الأقطار والتحول المقابل في الشكل أعلاه باللون الأزرق.
تعود فكرة استخدام سلسلة من التحولات في الخطوط بالنسبة لبعضها البعض في مشكلة البحث الغامض إلى التقنية المعروفة للكشف عن إشارات الرادار على خلفية التداخل ، والتي تنطوي على حساب وظيفة الارتباط المتبادل للإشارات اللاسلكية. تحدد وظيفة الارتباط المتبادل درجة تشابه نسخ إشارتين مختلفتين v (t) و u (t) ، وتنتقل بمرور الوقت بالنسبة لبعضها البعض وتعرف على أنها التكامل: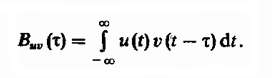
يتم حساب إجمالي عدد الأقطار بواسطة الصيغة:

أطوال الأقطار تساوي طول سلسلة البحث.
مجموعات المباراة
الوحدات التالية على التوالي في الأقطار من مصفوفة مصادفة تشكيل مجموعات من المباريات. فيما يلي مجموعات المطابقة لسلسلة البيانات "ABCD DEF JH" وسلسلة البحث "ABC DE J" - 4 مجموعات موجودة على أقطار مختلفة.

مصفوفات الإسقاط
يتم تعيين الأقطار لمصفوفة المطابقة ومجموعات المطابقة الموجودة بها على الأقسام المقابلة من سلسلة البحث وسلسلة البيانات ، وتشكيل مصفوفة إسقاط - سلسلة البحث وسلسلة البيانات ، على التوالي. على سبيل المثال ، ستبدو مصفوفات الإسقاط كما يلي:
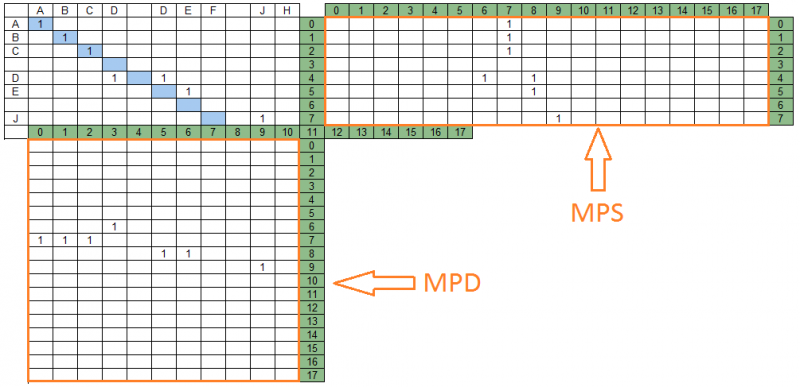
في الشكل أعلاه ، يوجد على يمين مصفوفة المطابقة مصفوفة الإسقاطات على سلسلة البحث - MPS ، أدناه - مصفوفة الإسقاطات على سلسلة بيانات MPD. عدد أعمدة MPS يساوي عدد صفوف MPD ويساوي عدد الأقطار في مصفوفة المطابقة - في المثال الخاص بنا ، هناك 18.
ابحث عن مجموعة نتائج من المجموعات
لحل المشكلة ، من الضروري العثور على مجموعة من المجموعات التي "تغطي" سلسلة البحث معظمها ، مع أقل تجزئة (أكبر عدد ممكن من الأجزاء) ، دون تقاطعات متبادلة في مصفوفات الإسقاط ، وسيكون تعيينها على سلسلة البيانات أقرب إلى سلسلة البيانات "الأصلية" - سلسلة البحث .
تقاطع المجموعات في مصفوفة الإسقاطفي مثالنا ، هناك مجموعات تتقاطع في مصفوفة MPS - في الشكل أدناه يتم تمييزها باللون الأحمر. علاوة على ذلك ، في مصفوفة MPD ، لا تتقاطع هذه المجموعات نفسها ، في الشكل الذي يتم تسليط الضوء عليه باللون الأخضر.
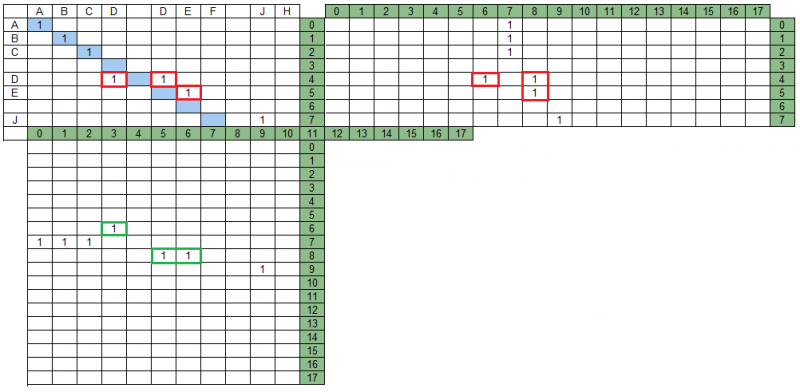
يشير البحث عن مجموعة المجموعات الناتجة إلى أنه لن يتم تضمين كل المجموعات فيه وأنه يمكن تعديل بعض المجموعات المتبقية (اقتطاعها) عند تحليل التقاطعات المتبادلة للمجموعات في الإسقاطات.
يمكن إجراء البحث عن مجموعة النتائج من خلال الانتقال إلى دورة "غير محدودة" (عدد التكرارات من الدورة لا يتجاوز عدد المجموعات) من
جدول جميع المجموعات ، حيث يتم وضع مجموعات مصفوفات المطابقة في البداية ، في كل تكرار سيتم تنفيذ الإجراءات التالية:
- اختيار الأفضل وفقًا لمعلمات معينة (اعتمادًا على سياق المشكلة التي يتم حلها) - في أبسط الحالات ، قد يكون هذا هو اختيار المجموعة الأولى من أكبر حجم التي تأتي عبر ؛
- وضع أفضل مجموعة في جدول مجموعات النتائج وإزالتها من جدول جميع المجموعات (يتم الزحف إلى صفوفها) ؛
- إزالة (أو اقتطاع) من جدول المجموعات التي تتقاطع مع أفضل مجموعة محددة في مصفوفات الإسقاط للمجموعات.
يتم عرض المجموعة المثلى من المجموعات على سبيل المثال لدينا في الشكل أدناه - يتم تمييز المجموعات المحددة باللون البرتقالي.

يتم تمييز المجموعة المحذوفة أثناء معالجة التقاطع (تقاطع في مصفوفة MPS مع أفضل مجموعة من التكرار الثاني) باللون الأحمر.
تبدو نتيجة البحث في صف البيانات كما يلي:

حساب معامل الأهمية
لتحديد نتائج البحث ، تتم مقارنة أطوال المجموعات التي تم العثور عليها مع أطوال الكلمات في سلسلة البحث (تقييم تكوين المجموعة) ، وكذلك الطول الإجمالي لسلسلة البحث مع طول المجموعات الموجودة في سلسلة البيانات. من المفترض أن تكون أهمية تقييم تكوين المجموعات الموجودة أعلى من أهمية تقدير المدى في صف البيانات ، والتي تؤخذ في الاعتبار في معاملات وزن الصيغة لحساب معامل الأهمية:

حيث يتم حساب معامل تكوين المجموعة كنسبة من مجموع أطوال المربعة للمجموعات التي تم العثور عليها إلى مجموع أطوال الكلمات المربعة في سلسلة البحث:

عامل الطول هو نسبة طول سلسلة البحث إلى الطول الإجمالي للمجموعات التي تم العثور عليها في سلسلة البيانات. إذا كانت القيمة التي تم الحصول عليها بهذه الطريقة أكبر من 1 ، يتم أخذ القيمة العكسية:

على سبيل المثال لدينا:

النطاق المقدر للحوسبة
العمليات الأكثر كثافة في استخدام الموارد هي:
- تحديد مصفوفة المطابقة M - يتم تعريف عدد عناصر المصفوفة على أنه منتج لطول سلسلة البحث بطول سلسلة البيانات: L * L؛
- تعريف مصفوفات الإسقاط على سلاسل البيانات والبحث - سيكون عدد عناصر المصفوفة من أجل MPS: (L + L - 1) * L ، بالنسبة إلى MPD: (L + L - 1) * ؛
- تكوين جدول جميع المجموعات - لن يتجاوز عدد المجموعات القيمة L * L / 2 ؛
- ابحث عن مجموعة المجموعات الناتجة - لا يتجاوز عدد التكرارات للدورة العدد الأولي للمجموعات ، أي L * L / 2.
وبالتالي ، سيكون المبلغ الإجمالي للحسابات مضاعفًا لمنتج طول سلسلة البحث حسب طول سلسلة البيانات:

تعد خطية مقدار الحساب بالنسبة لحجم البيانات المصدر حجة مهمة لصالح التطبيق العملي للخوارزمية.
استقامة
تجدر الإشارة إلى أن الخطي يرجع إلى إجراء مبسط للعثور على مجموعة من المجموعات الناتجة. في الحالة العامة ، إذا أخذنا في الاعتبار جميع الخيارات الممكنة لوضع المجموعات على صف البيانات ، مع مراعاة خيارات معالجة التقاطع المحتملة وتحديد أفضل
مجموعة من المجموعات من مجموعة الممكن ، بدلاً من اختيار
مجموعة واحدة في كل تكرار للدورة ، فإن كمية العمليات الحسابية ستتوقف عن أن تكون خطية فيما يتعلق بالحجم مصدر البيانات. الاعتماد غير الخطي لكمية الحساب على حجم البيانات المصدر يحد بشكل كبير من احتمالات التطبيق العملي.
العثور على التوازن
لضمان التوازن الأمثل بين جودة البحث والحاجة إلى الموارد ، من المهم اختيار منهجية البحث الصحيحة لمجموعة المجموعات الناتجة ، والتي يمكن ، كقاعدة عامة ، القيام بها باستخدام ميزات سياق المشكلة التي يتم حلها.
تم نشر موقف تجريبي على موقع
textradar.ru حيث يمكنك اختبار تشغيل الخوارزمية.
مقارنة مع نظائرها:
مقارنة خوارزمية البحث الغامض TextRadar مع نظائرها: Lucene ، Sphinx ، Yandex ، 1C