واحدة من أصعب المهام في أنظمة التصميم بمساعدة الكمبيوتر هي فيليه عند نمذجة الكائنات ذات الأشكال المعقدة. لبناء فيلت ، وكذلك لجميع الهندسة في كندي ، الأساسية الهندسية هي المسؤولة.

من وجهة نظر مطور kernel ، يستحيل تغطية جميع خيارات التقريب بسبب تنوعها غير المحدود. يضيف علماء الرياضيات لدينا باستمرار حالات خاصة جديدة إلى قلب C3D ، وقد قاموا مؤخرًا بتقريب ثلاثة وجوه (أو التقريب الكامل).

تقول آنا لاديلوفا ، عالمة رياضيات ومبرمجة في C3D Labs ، ما هو تعقيدها وكيف تعمل الخوارزمية؟

ما هو التقريب الكامل؟

لنفترض أن لدينا جسمًا به ثلاث سلاسل من الوجوه - المركزية (العليا) والجانبية (اليمنى واليسرى). يجب استبدال الوجه المركزي بسطح فيليه يلائم بسلاسة الوجوه الجانبية المجاورة. هذا السطح الجديد سيكون التقريب الكامل. بشكل عام ، له دائرة نصف قطرها متغير يتم اكتشافها تلقائيًا.



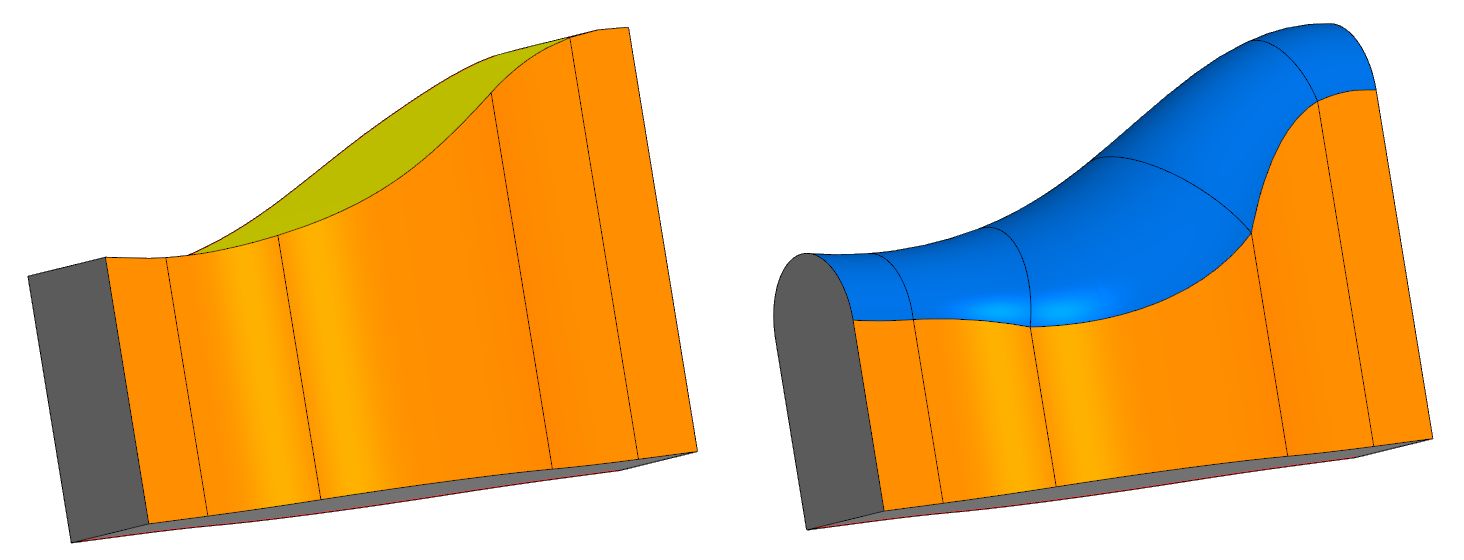
في العديد من أنظمة CAD المعروفة ، يتم تنفيذ عملية الشرائح الكاملة ، لكن لم يتم الكشف عن رياضياتها.


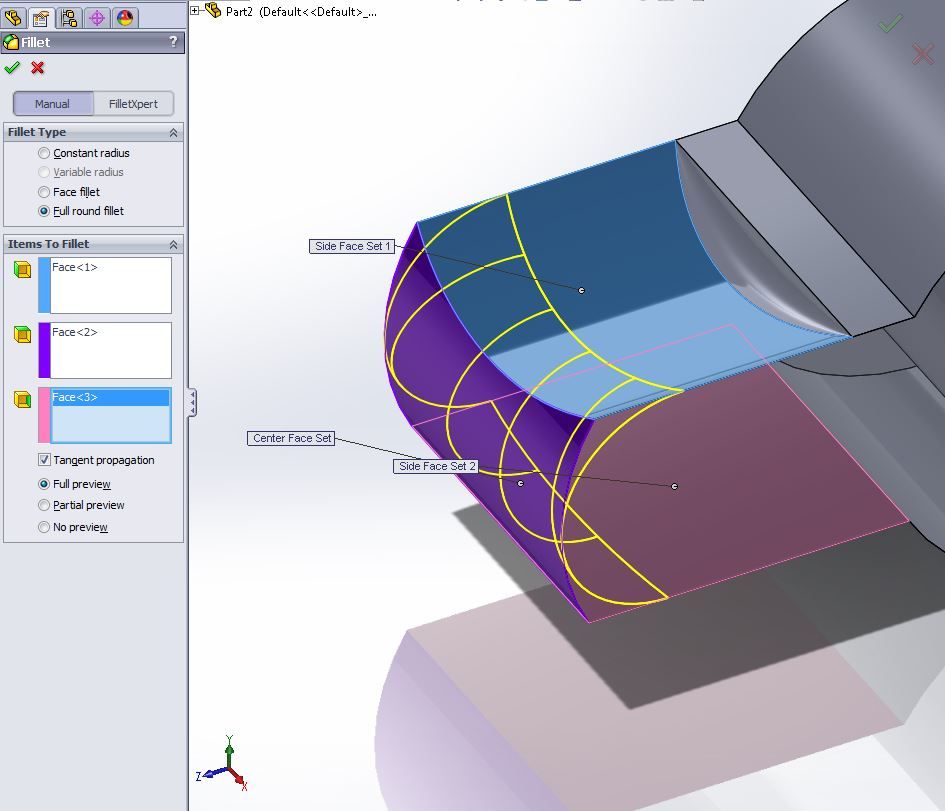Solidworks عملية فيليه جولة كاملة

لذلك ، قمنا بتطوير الخوارزمية الخاصة بنا. ويختلف عن خوارزميات المطورين الآخرين.

العمليات ، على الرغم من أنها تسمى نفسها ، تؤدي إلى نتائج مختلفة قليلاً. هذا يشير إلى أن SolidWorks يعطي تعريفًا مختلفًا لتقريب الوجوه الثلاثة.


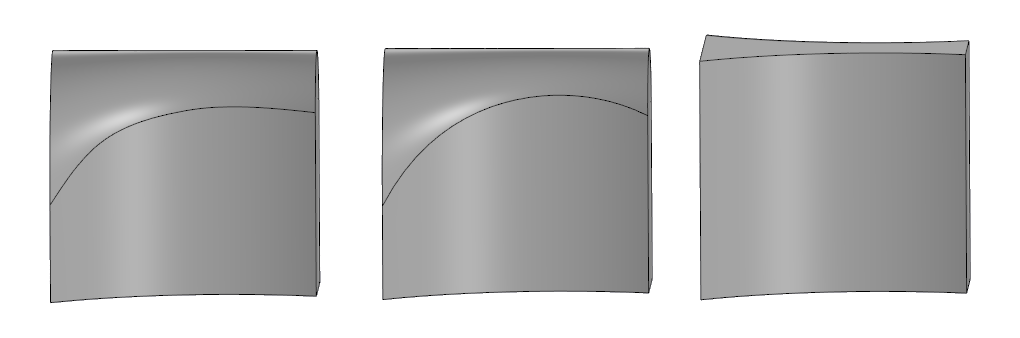على اليمين يوجد النموذج الأصلي ، في الوسط هو التقريب الكامل في SolidWorks ، على اليسار - في C3D.

خوارزمية التقريب كاملة

تتضمن مهمة إنشاء أي نوع من الشرائح عدة مراحل:

1. قم بتقسيم السلسلة المحددة إلى مكونات أولية (لتقريب الوجوه الثلاثة ، تكون ثلاثة وجوه بالضبط: اليسار واليمين والوسط).
2. باستمرار ترتيب المكونات الأولية.
3. بناء سطح فيليه لكل مكون الابتدائية.
4. غرزة الأسطح فيليه المجاورة مع الأضلاع.
5. لمعالجة المقاطع النهائية لسلسلة الشرائح ، أي توصيلها بشكل صحيح بالجسم المعدل.

النقطة الأساسية في هذا الإجراء هي الخطوة الثالثة: بناء سطح فيليه لثلاثة وجوه معينة.

لبناء السطح المرغوب فيه ، من الضروري أولاً تحديد المنحنيات التي تلامس فيليه كل وجه من الوجوه الثلاثة. في الحالة العامة ، لا يمكن بناء هذه المنحنيات إلا كخطوط مرور تمر عبر نقاط معروفة يتم حسابها مقدمًا.

فكر في كيفية حساب ثلاث نقاط - واحدة على كل شريحة.


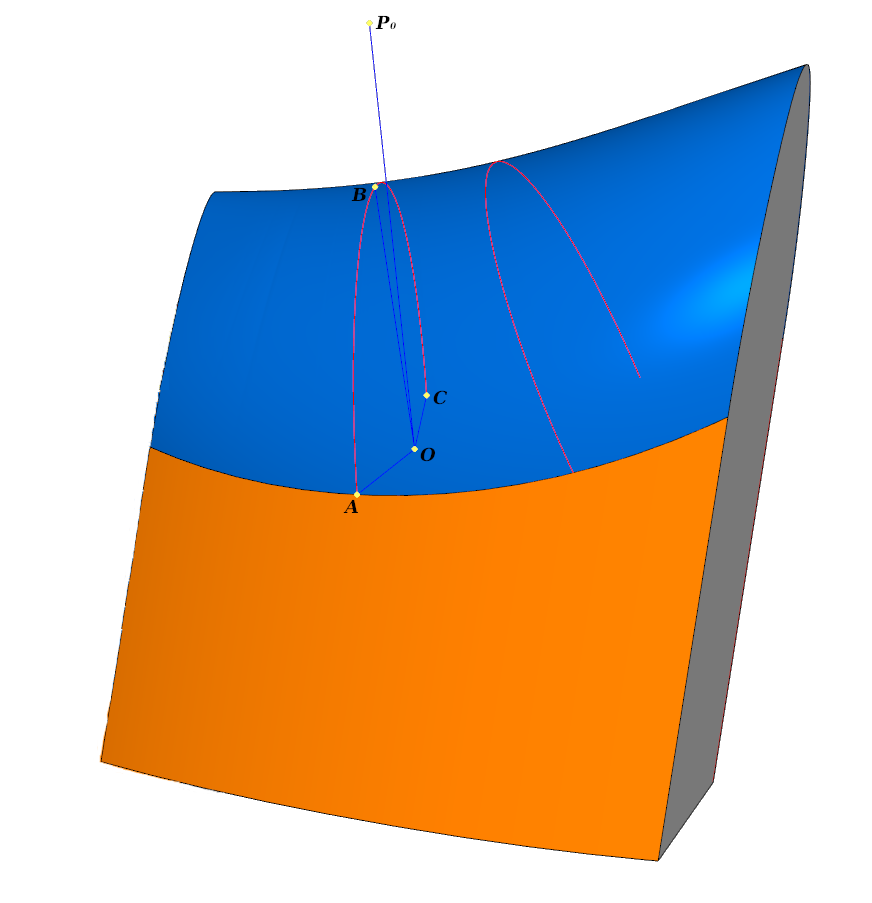
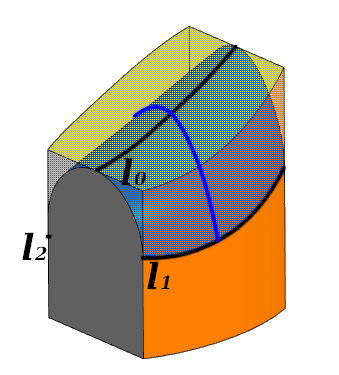المعالجة الأولية. شرائح فيليه كل من الوجوه الثلاثة على طول المنحنيات ل ₀ ؛ ₁ ل ₂ . يظهر الخط الأزرق المقطع العرضي

في كل مقطع عرضي $$$ABC$ :

• $$$OA = OB = OC$ - تحسب تلقائيا
• $$$الزراعة العضوية ، OB ، OC$ متعامد على الطائرات المماسية للأسطح عند النقاط المقابلة
• $$$ع$ ₀ - نقطة مرساة ، وتقع في الطائرة $$$ABC$ .

نحدد الأسطح الأولية للوجوه المركزية واليسرى واليمنى بواسطة متجهات نصف القطر في مجال معين من التعريف. دع الأسطح الجانبية محددة بواسطة ناقلات نصف قطرها $$$ص$ ₁ $$$(u، v)$ و $$$ص$ ₂ $$$(z ، w)$ و المركزية $$$ص$ ₀ $$$(س ، ذ)$ . نقدم المعلمة العددية الإيجابية $$$د$ .

دلالة بواسطة $$$ن$ ₀ $$$(س ، ذ)$ . $$$ن$ ₁ $$$(u، v)$ . $$$ن$ ₂ $$$(z ، w)$ الحالة الطبيعية واحدة للأسطح المقابلة ، موجهة "الداخل".


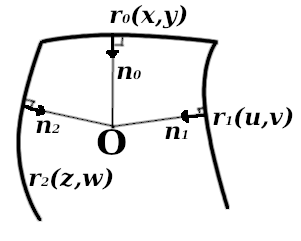تقاطع "القسم" عند بناء فيليه

نحن نطلب أن نهايات هذه الأوضاع الطبيعية امتدت فيها $$$د$ مرات ، وضرب نقطة واحدة $$$يا دولا$ .

فيما يتعلق بالهندسة التفاضلية ، يمكن صياغة متطلباتنا بواسطة نظام من سبع معادلات مع سبع معلمات:

$$$dn$ ₀ $$$(س ، ذ)$ = $$$dn$ ₁ $$$(u، v)$ .
$$$dn$ ₀ $$$(س ، ذ)$ = $$$dn$ ₂ $$$(z ، w)$ .
( $$$ص$ ₀ $$$(س ، ذ)$ - $$$ع$ ₀ $$$ص$ ₁ $$$(u، v)$ - $$$ع$ ₀ $$$ص$ ₂ $$$(z ، w)$ - $$$ع$ ₀ ) = $$$0$ .

حيث

• $$$د$ - نصف قطر متغير
• $$$ع$ ₀ - نقطة الربط
• $$$x ، y ، u ، v ، z ، w$ - المتغيرات من منطقة تعريف المعلمة.

باستخدام خوارزميات الطرق العددية (على سبيل المثال ، طريقة نيوتن) ، نجد حلاً لهذا النظام: $$$x$ ₀ $$$ذ$ ₀ $$$u$ ₀ $$$v$ ₀ $$$z$ ₀ $$$w$ ₀ $$$د$ ₀

يحدد الحل نقاط اللمس مع الأسطح:

• $$$ص$ ₀ ( $$$x$ ₀ $$$ذ$ ₀ )
• $$$ص$ ₁ ( $$$u$ ₀ $$$v$ ₀ )
• $$$ص$ ₂ ( $$$z$ ₀ $$$w$ ₀ )

وكذلك دائرة نصف قطرها $$$د$ ₀

من خلال تشغيل مجموعة من النقاط $$$ع$ ₀ ، نحصل على مجموعات ثلاثية من نقاط الظل مع الأسطح التي يمكنك من خلالها استعادة "منحنيات اللمس" $$$ل$ ₀ $$$ل$ ₁ $$$ل$ ₂ كما يطير هيرميت من خلال النقاط المحسوبة.

النطاق [ $$$t$ _دقيقة، $$$t$ _{كحد أقصى} ] جميع المنحنيات هي نفسها ، والمعلمة $$$t$ _أنا أتوافق مع نقطة $$$ص$ _0I، $$$ص$ _1I، $$$ص$ _2i . علاوة على ذلك ، يتم استخدام هذه المنحنيات لحساب المقطع العرضي المطلوب للشرائح.

نحن إصلاح بعض المعلمة $$$t$ وحساب النقاط لذلك:

• $$$ص$ ₀ $$$(x (t) ، y (t)) ،$
• $$$ص$ ₁ $$$(u (t) ، v (t)) ،$
• $$$ص$ ₂ $$$(z (t) ، w (t))$ .

نبني منحنى خدد مرورا بهذه النقاط ونواقل طبيعية متعامدة لهم $$$ن$ ₀ $$$(x (t) ، y (t))$ . $$$ن$ ₁ $$$(u (t) ، v (t))$ . $$$ن$ ₂ $$$(z (t) ، w (t))$ على التوالي.

إذا تم تغيير بيان المشكلة بشكل طفيف وتم البحث عن المنحنى في نقاط معينة ونواقل الظل في هذه النقاط ، فيمكن العثور على الطرق التي يمكن بها تنفيذ هذا الخط ، على سبيل المثال ، في كتاب نيكولاي جولوفانوف "النمذجة الهندسية".

يصف الكتاب بالتفصيل طرق تقريب حافة الجسم ، على وجه الخصوص ، يظهر أنه يمكن تحقيق المقطع العرضي للتقريب على أنه منحنى NURBS المحدد بثلاث نقاط. إذا تم تقريب ثلاثة وجوه ، فسيتم تحديد منحنى مماثل بخمس نقاط.

لذلك ، لكل معلمة $$$t$ يمكننا تحديد مجموعة من النقاط لبناء NURBS ، وبالتالي ، تحديد كل نقطة من المقطع العرضي لسطح فيليه. وبالتالي ، يتم حل مشكلة بناء السطح تماما.

في وصف هذا الجزء من الخوارزمية ، يبقى سؤال صغير - كيفية "اختيار" مجموعة من النقاط $$$ع$ ₀ يقابل المقطع العرضي الذي من خلاله سيكون من السهل استعادة "منحنيات اللمس" $$$ل$ ₀ $$$ل$ ₁ $$$ل$ ₂ ؟

يبدو من المنطقي اصطحابهم مع بعض المنحنى المحدد مسبقًا. لن ندخل في تفاصيل بناء هذا المنحنى ، نلاحظ فقط أنه يجب أن يكون سلسًا ، دون تقاطعات ذاتية و "متوسط" سلاسل الحواف التي تربط الوجه المركزي على اليسار وعلى اليمين.


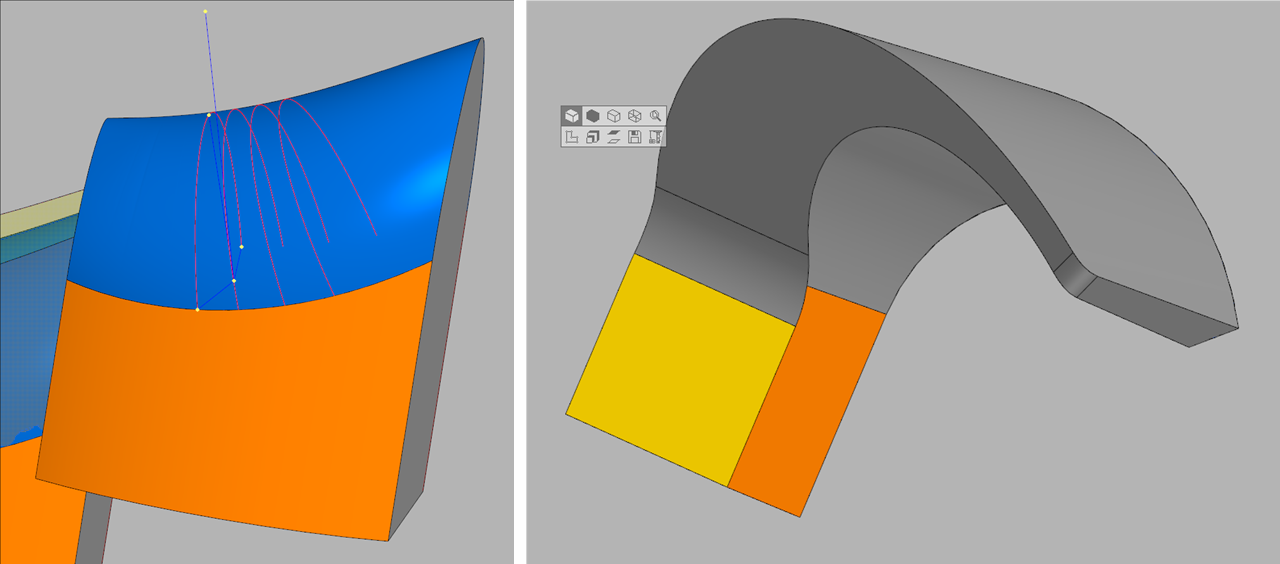اليسار ، مستعرضة ، تعتمد على نقطة $$$ع$ ₀
على اليمين ، يمكن أن تكون الأشكال معقدة للغاية ، لذا فإن اختيار المنحنى "المساعد" بشكل صحيح يعد مهمة منفصلة.

الآن بعد أن أصبحنا قادرين على بناء أسطح فيليه لأبسط الحالات الابتدائية ، يمكننا الانتقال إلى مشكلة أكثر تعقيدًا: بناء سطح لسلسلة من الوجوه.
المشكلة الرئيسية هنا هي "خياطة" الأسطح المجاورة بطريقة سلسة. هذه هي الخطوة الرابعة من الخوارزمية.

تكمن الصعوبة بالتحديد في سلاسة الارتباط المتشابك ، حيث أن الأسطح مبنية ببيانات أولية مختلفة. لضمان السلاسة ، يتعين على المرء اللجوء إلى الحيل المختلفة: تغيير اتجاه وطول ناقلات المشتقات في الاتجاه الطولي على مسافة معينة من الحدود ، وتغيير قيم مشتقات وظائف الوزن على الحدود ، إلخ. النتائج واضحة في الشكل: خطوط حمار وحشي أكثر سلاسة تتوافق مع سطح أكثر سلاسة.




أعلاه نموذج بدون خوارزمية تجانس. أدناه - بعد تطبيق الخوارزمية.

يؤدي

نتيجة لبحوثنا ، فإن اللب الهندسي C3D قادر على بناء مقطع دائري ، منحنيات الدعم ، وتقريب ثلاثة وجوه ؛ يعرف كيفية سلاسة السطح عن طريق اختيار معلمة ؛ يعرف جزئياً كيف ينضم بسلاسة إلى شرائح فيليه مجاورة.


المؤلف - آنا لاديلوفا ، دكتوراه ، عالم رياضيات / مبرمج C3D Labs