كيف يعمل تشفير المنحنى الإهليلجي في TLS 1.3

تنبيهات القارئ:

من أجل (إلى حد ما) تبسيط عملية الوصف وتشديد حجم المقالة التي سنكتبها ، من الضروري تقديم ملاحظة مهمة وتحديد القيد الأساسي على الفور - كل ما سنخبرك به اليوم حول التطبيق العملي الجانب من إشكالية قابلة للحياة فقط من حيث TLS 1.3. بمعنى أنه في حين أن شهادة ECDSA ستظل تعمل في TLS 1.2 إذا كنت ترغب في ذلك ، فتوفر التوافقية الخلفية ، ووصف عملية المصافحة الفعلية ، وشفرات التشفير ومعايير خادم العميل تغطي TLS 1.3 فقط. بالطبع ، هذا لا يتعلق بالوصف الرياضي للخوارزميات التي تكمن وراء أنظمة التشفير الحديثة.

لم يكتب هذا المقال عالم رياضيات ولا مهندسًا - على الرغم من أن تلك ساعدت في إيجاد طريقة للتغلب على الرياضيات المخيفة واستعراض هذه المقالة. شكرا جزيلا لموظفي Qrator Labs.

( E lliptic C urve) D iffie- H ellman ( E phemeral)

تراث ديفي - هيلمان في القرن 21

بالطبع ، لقد بدأ هذا مع ديفي ولا هيلمان. ولكن لتوفير جدول زمني صحيح ، نحتاج إلى الإشارة إلى التواريخ والأحداث الرئيسية.

كان هناك العديد من الشخصيات الرئيسية في تطوير التشفير الحديث. وأبرزها أن كلا من ألان تورنج وكلود شانون قاما بعمل لا يصدق في مجال نظرية الحوسبة ونظرية المعلومات وكذلك تحليل التشفير العام ، وكلاهما ديفي وهيلمان ، ينسب إليهما رسمياً التوصل إلى فكرة المفتاح العمومي (أو ما يسمى تشفير غير متماثل) (على الرغم من أنه من المعروف أنه تم إحراز تقدم كبير في المملكة المتحدة في التشفير الذي ظل سريًا لفترة طويلة جدًا) ، مما جعل هؤلاء السادة الرواد.

في ماذا بالضبط؟

حسنا ، هذا قد يبدو غريبا. ومع ذلك ، قبل 6 نوفمبر 1976 ، لم تكن هناك معرفة عامة بأنظمة تشفير المفتاح العام. كان ويتفيلد ديفي ومارتن هيلمان (وبالفعل ، رالف ميركل) - علماء الرياضيات ومهندسو الكمبيوتر وعشاقوه ، بالإضافة إلى علماء التشفير.

بالنسبة لأولئك غير المدركين - نظرًا للدور الذي لعبه تحليل الشفرات خلال الحرب العالمية الثانية وتأثيره الهائل على الحفاظ على سرية المعلومات ، فإن البلدين اللذين اعتقدا أنهما كانا يتمتعان بمعرفة متقدمة بالتشفير - أدرجتا الولايات المتحدة والمملكة المتحدة التشفير في قوائم الذخائر الخاصة بهما واستفادتا منها. فرض حظر كبير على الصادرات (يضعف في الوقت نفسه تنفيذ التشفير للاستخدام المحلي الخاص والتجاري). لهذا السبب ، لم يتم التعرف على الباحثين في المملكة المتحدة الذين يعملون في تقنية تبادل المفاتيح غير المتماثلة في مقر الاتصالات الحكومية وتطوير مخطط مماثل لهذا الاختراع حتى عام 1997 ، عندما أصبحت القيود المفروضة على خوارزميات التشفير ووصفها غير فعالة.

العودة إلى المخترعين المزدوجين - ما الذي أحدث ثورة في ديفي وهيلمان على وجه التحديد؟

دعنا نلقي نظرة على ورقتهم الأصلية ، مع توضيح القفزة العملاقة التي قدموها (حتى من الناحية النظرية بورقة بحثهم):

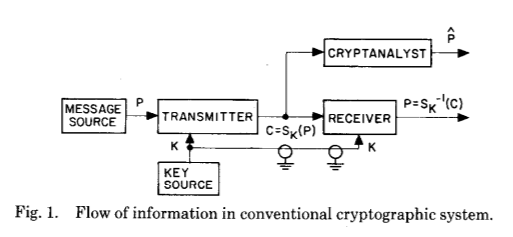
و التالي:

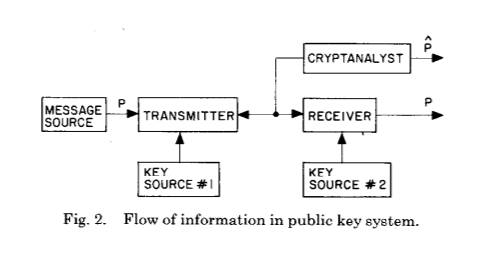
توضح هاتان الصورتان تمامًا التغير الضخم الذي أدخله ويتفيلد ديفي ومارتن هيلمان بعد تشفير وتحليل التشفير منذ قرون من التطور - إنشاء مفتاح سري مشترك نتيجة حساب تشفير.

دعونا نلقي نظرة على صورة أخرى جيدة مع الألوان:



وهذا ما يفسر ما يحدث. قبل اختراع اتفاقية مفتاح Diffie و Hellman ، كان هناك مفتاح متماثل واحد فقط - تم استخدامه لتشفير الرسالة وفك تشفيرها. إذا كنت ترغب في إعطاء شخص ما مثل هذا "المفتاح" ، فيجب نقله عبر قناة "آمنة". يمكنك أن تتخيل كل القيود المفروضة على مخطط الجيل السابق هذا فورًا - فأنت بحاجة إلى قناة آمنة قائمة بالفعل ، ولا يمكنك إعادة استخدام المفتاح ، ومن الناحية المثالية ، يجب أن يكون طول المفتاح هو نفسه طول الرسالة.

أثبت كلود شانون في كتابه المصنف زمن الحرب " نظرية الاتصالات لأنظمة السرية " أن جميع الأصفار غير القابلة للكسر من الناحية النظرية يجب أن يكون لها نفس المتطلبات مثل الوسادة التي لمرة واحدة - والمعروفة باسم تشفير فيرنام ، من قبل مؤلف هذا الشفرة المتناظرة متعددة الطبقات.

مرة أخرى ، سوف نلقي نظرة على الورقة الأصلية:


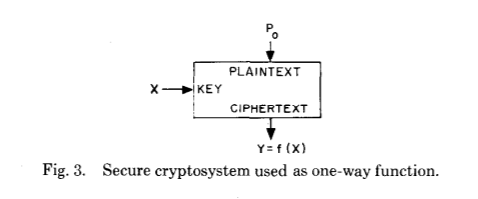
قبل أن نذهب إلى أبعد من ذلك ، دعونا نسأل أنفسنا - كيف اثنين ، حتى لو رائعة ، ومع ذلك ، جاء البشر مثل هذا التحسن الكبير في مجال تطبيقي مع مثل هذا التاريخ ، وخاصة في وقت الحرب؟
حسنًا ، بسبب:

• نظرية المعلومات ، صاغها كلود شانون ؛
• تأثرت نظرية الحوسبة بأهمها ألونزو تشيرش وجون فون نيومان وألان تورينج ؛
• والأهم من ذلك ، أن نظرية الحوسبة تعتمد في الغالب على أعمال تورينج ، والتي يمكن أن نقول أن جميعها تطورت ونضجت في نفس الفترة من القرن العشرين. ذكر كل من ديفي وهيلمان كلود شانون كأهم المؤثر في عملهم.

يوضح " الأمن العالمي " الخاص بـ Lenstra مقدار الطاقة اللازمة "لكسر" نظام التشفير المتماثل بأطوال رئيسية مختلفة. لقد اتضح أن كسر مفتاح منحنى إهليلجي يبلغ طوله 228 بتًا سيتطلب نفس القدر من الطاقة اللازمة لغلي كل الماء على الأرض. ومع ذلك ، فهي صالحة فقط عند النظر في الخوارزميات والأجهزة المعروفة ، كما هو واضح ، لا أحد يعرف ما إذا كانت الخوارزميات أو الأجهزة أكثر كفاءة بشكل كبير. يشبه مفتاح EC 228 بت مفتاح RSA الذي يبلغ طوله 2380 بت ، وأكثر من ذلك في وقت لاحق. على الرغم من أن كلا من RSA و EC يستخدمان في هذا التقدير في نظام تشفير غير متماثل ، فإن أطوال المفاتيح هذه تعادل إلى حد ما مفتاح تشفير 128 بت متماثل.

من السهل أن نتخيل أن شيئًا ما "يصعب حسابه" يتطلب الكثير من الطاقة و / أو الوقت اللازم للحساب. نميل إلى الاعتقاد بأن أجهزة الكمبيوتر يمكنها "حساب كل شيء" ، لكن اتضح أنه غير صحيح. أولاً ، توجد أمثلة غير قابلة للإلغاء ، مثل مشكلة التوقف ، على الرغم من أنه في مجال التشفير ، يمكننا تجنب هذا الخطأ. ثانياً ، إذا أخذنا في الاعتبار الوقت اللازم لخوارزمية معينة لتشغيلها ، فقد تكون مرتفعة بشكل تعسفي. هذا هو ما نستغله في التشفير. تعتبر المشكلة "سهلة" لحساب ما إذا كان الوقت اللازم لتشغيل الخوارزمية المعنية يعتمد على حجم الإدخال (المقاس بالبتات) مثل كثير الحدود:$$ $ inline $ T (n) = O (n ^ k) $ inline $ ، لبعض ثابت إيجابي$$ $ مضمنة $ k $ مضمنة . في مجال نظرية التعقيد الحسابي ، تشكل هذه المشكلات فئة التعقيد P.

تعد فئة التعقيد P أمرًا مركزيًا تقريبًا ، حيث إنها تمثل مشكلة وجود خوارزمية زمنية متعددة الحدود حتمية. فئة التعقيد الأخرى هي NP (المشكلات التي يصعب حسابها) ، والتي تمثل مجموعة من مشكلات القرار ، أي المشكلات التي تتطلب إجابة "نعم" أو "لا" ، والتي لها إثبات يمكن التحقق منه في وقت متعدد الحدود. ترى كلمة "إثبات" هنا؟ هذا هو المكان الذي نصل فيه إلى وظائف trapdoor ، التي تنتمي إلى فئة التعقيد NP.


ائتمانات: xkcd

وظائف أحادية الاتجاه وظائف Trapdoor

بحكم التعريف ، فإن الوظيفة أحادية الاتجاه هي وظيفة يسهل حسابها على كل إدخال ولكن يصعب عكسها ، أي حساب الإدخال الأصلي الناتج فقط. تشير كلمة "سهل" و "صعب" إلى تعريفات نظرية التعقيد الحسابي أعلاه. ومن المثير للاهتمام ، أن وجود وظائف أحادية الاتجاه لم يتم إثباته (رياضيا) لأن وجودها سيثبت أن فصول التعقيد P و NP ليست متساوية ، في حين أن P تساوي NP أو لا تعد في الوقت الحاضر مشكلة مفتوحة. لذلك ، ضع في اعتبارك أن كل التشفير الحديث يعتمد على فرضيات غير مثبتة.

الآن ، قدم ديفي وهيلمان في ورقتهما الأصلية جيلًا آخر من الوظائف أحادية الاتجاه التي أطلقوا عليها "وظائف trapdoor". كيف تختلف؟
كما يفسرون في الورقة التاريخية الخاصة بهم:

في نظام التشفير العمومي بالمفتاح العمومي ، يخضع تشفير وفك تشفير المفاتيح بواسطة مفاتيح مميزة ، E و D ، بحيث تكون الحوسبة D من E غير قابلة للحساب (على سبيل المثال ، تتطلب$$ $ inline $ 10 ^ {100} $ inline $ تعليمات). يمكن الكشف عن مفتاح التشفير E [في دليل] دون المساس بمفتاح فك التشفير D. يمكّن ذلك أي مستخدم للنظام من إرسال رسالة إلى أي مستخدم آخر مشفّر بطريقة تمكن المستلم المقصود فقط من فك تشفيره. .. ربما تمثل مشكلة المصادقة حاجزًا أخطر أمام التبني العالمي للاتصالات السلكية واللاسلكية للمعاملات التجارية من مشاكل التوزيع الرئيسية ... [...] هي في صلب أي نظام ينطوي على عقود وفواتير.

وفقًا للاتفاقية ، يتم استخدام أحرف التشفير "Alice" و "Bob" (البحث عن اتصال آمن) بشكل متكرر لشرح مفهوم المفتاح العام. يتفق أليس وبوب على الأعداد الصحيحة الكبيرة$$ $ inline $ n $ inline $ و$$ $ مضمنة $ g $ مضمنة مع$$ $ inline $ 1 <g <n $ inline $ . الاختيار يؤثر على أمن النظام. "معامل$$ $ inline $ n $ inline $ يجب أن يكون رئيس الوزراء. الأهم من ذلك$$ $ inline $ (n-1) / 2 $ inline $ يجب أن تكون أيضًا علامة <...> و$$ $ مضمنة $ g $ مضمنة يجب أن يكون معامل الجذر البدائي$$ $ inline $ n $ inline $ <...> [و]$$ $ inline $ n $ inline $ يجب أن يكون <...> 512 بت على الأقل. " يمكن ذكر بروتوكول Diffie - Hellman بشكله الأولي في 5 خطوات.

1. أليس تختار$$ $ مضمنة $ x $ مضمنة (عدد صحيح عشوائي كبير) ويحسب$$ $ inline $ X = g ^ x \ bmod n $ inline $
2. اختار بوب$$ $ مضمنة $ y $ مضمنة (عدد صحيح عشوائي كبير) ويحسب$$ $ inline $ Y = g ^ y \ bmod n $ inline $
3. أليس يرسل$$ $ مضمنة $ X $ مضمنة إلى بوب ، في حين يرسل بوب$$ $ مضمنة $ Y $ مضمنة إلى أليس (يحتفظون$$ $ مضمنة $ x $ مضمنة و$$ $ مضمنة $ y $ مضمنة سر من بعضنا البعض)
4. أليس يحسب$$ $ inline $ k = Y ^ x \ bmod n $ inline $
5. بوب يحسب$$ $ inline $ k '= X ^ y \ bmod n $ inline $

نتيجة لذلك ، تمتلك أليس وبوب نفس القيمة$$ $ مضمنة $ k = $ 'مضمنة $ هذا بمثابة سر مشترك.

وظيفة Trapdoor هي وظيفة أحادية الاتجاه تجعل من الممكن العثور على عكس ذلك إذا كان لدى الشخص معلومات خاصة تسمى "trapdoor". يبدو الأمر سهلاً ، على الرغم من صعوبة العثور على مثل هذه الوظائف - تم العثور على الطريقة الأولى الممكنة في تنفيذ خوارزمية تشفير التشفير غير المتماثل للمفتاح العام المسمى RSA بعد منشئيها: Ron Rivest و Adi Shamir و Leonard Adleman.

RSA

في RSA ، تستند صلابة قلب الوظيفة إلى حقيقة أن التخصيم (إيجاد المضاعفات الأولية للرقم) يستغرق وقتًا أطول بكثير من الضرب ، أو يجب أن نقول هنا أنه لا توجد طريقة متعددة الحدود لتقسيم أعداد صحيحة كبيرة على كمبيوتر كلاسيكي تم العثور عليها ، ومع ذلك ، لم يثبت أن لا شيء موجود.

في RSA ، كما هو الحال في أي نظام تشفير بالمفتاح العام ، يوجد مفتاحان: عام وخاص. تأخذ RSA رسالة الإدخال (ممثلة كسلسلة بت) وتطبق عملية حسابية (معامل التسوية عددًا صحيحًا كبيرًا) عليها للحصول على نتيجة تبدو غير قابلة للتمييز من عشوائي. يأخذ فك التشفير هذه النتيجة ويطبق عملية مماثلة لاستعادة الرسالة الأصلية. في التشفير غير المتماثل ، يتم التشفير باستخدام المفتاح العمومي وفك التشفير مع المفتاح الخاص.

كيف؟ لأن المعاملات تنتمي إلى مجموعة دورية محددة (مجموعة من الأعداد الصحيحة مع الضرب في الحساب المعياري). لا يتعامل الحواسب مع الأرقام الكبيرة بشكل تعسفي ، ولكن لحسن الحظ ، فإن مجموعتنا الدورية من الأعداد الصحيحة هي إجراء عملية تسمى "التفاف حول" - يتم تغليف عدد أكبر من الحد الأقصى المسموح به حولها برقم في النطاق الصالح الذي نعمل فيه . يتيح لنا ذلك العمل بمفاتيح "لا تزيد عن" الطول. في مجموعات الاهليلجيه منحنى الاهليلجيه ، تستخدم المجموعات الدورية (المضاعفة) أيضًا ولكن يتم إنشاؤها بطريقة مختلفة بعض الشيء كما سنرى لاحقًا.

ما تقوم به RSA بشكل أساسي هو أخذ رقمين أوليين كبيرين وضربهما للحصول على ما يسمى بالمعامل. جميع الأرقام الأخرى التي يتعين التعامل معها تقع بين الصفر والمعامل. المعامل هو أن يكون جزءًا من المفتاح العمومي ، ويحدد طوله طول المفتاح. الجزء الثاني من المفتاح العمومي هو رقم يتم اختياره بين الصفر ومجموع Euler (تطبيق RSA الحديث يأخذ مجمل Carmichael بدلاً من Euler) من المعامل مع بعض القيود الإضافية. أخيرًا ، يتم حساب المفتاح الخاص عن طريق حل بعض المعادلات المعيارية. لتشفير رقم ، نرفعه ببساطة إلى القوة المساوية للمفتاح العام ، وللفك تشفير الرقم ، نرفعه إلى القوة المساوية للمفتاح الخاص. بفضل الطبيعة الدورية للمجموعة ، نعيد الرقم الأولي.

هناك مشكلتان مهمتان في RSA في الوقت الحاضر ، أحدهما نتيجة للآخر. عندما ينمو طول المفتاح (أي عدد وحداته) ، فإن عامل التعقيد لا ينمو بالسرعة التي قد يتوقعها المرء. ذلك بسبب وجود خوارزمية عامل فرعي (ولكن لا يزال متعدد الحدود ). لذلك ، من أجل الحفاظ على مستوى أمان مناسب ، يجب أن ينمو طول مفتاح RSA بشكل أسرع بعض الشيء من طول مفتاح ECC. هذا هو السبب في أن معظم مفاتيح RSA الواسعة الانتشار هذه الأيام إما 2048 أو 3072 بت.

بعد ذلك بقليل ، سنرى بأرقام كيف يؤثر طول المفتاح على الكفاءة الكلية لنظام التشفير عن طريق مقارنة شهادة RSA و ECDSA الموقعة مع سلطة Let's Encrypt.

( E lliptic C urve) D igital S الإشعال خوارزمية

أدى البحث عن وظيفة trapdoor أفضل في نهاية المطاف إلى جعل cryptographers يتطور بنشاط في فرع منتصف الثمانينيات من الرياضيات المخصص لمنحنيات إهليلجية.

ستكون المهمة النهائية لوصف تشفير المنحنى الإهليلجي في مقال واحد ، لذلك لن نقوم بذلك. بدلاً من ذلك ، دعنا نلقي نظرة على وظيفة trapdoor منحنى إهليلجي بناءً على مشكلة اللوغاريتم المنفصلة.

هناك العديد من الاشعارات والمزيد من المقدمات المتعمقة في تشفير المنحنى الإهليلجي ، ونحن نوصي بشكل خاص بـ "ECC: مقدمة لطيفة" من Andrea Corbellini إذا كنت مهتمًا بالرياضيات.

ما يهمنا هو معلمات "بسيطة".

يتم تعريف المنحنى الإهليلجي بمعادلة مثل هذا:$$ $ inline $ y ^ 2 = x ^ 3 + ax + b $ inline $
هناك حاجة إلى مثل هذا المنحنى لإنشاء مجموعة فرعية دورية على حقل محدود. لذلك ، يتم استخدام المعلمات التالية:

• رئيس الوزراء$$ $ inline $ p $ inline $ الذي يحدد حجم الحقل المحدود ؛
• المعاملات$$ $ inline $ a $ inline $ و$$ $ مضمنة $ b $ مضمنة $ لمعادلة المنحنى الإهليلجي.
• النقطة الأساسية$$ $ مضمنة $ g $ مضمنة الذي يولد المجموعة الفرعية المذكورة ؛
• الترتيب$$ $ inline $ n $ inline $ من المجموعة الفرعية ؛
• العامل المساعد$$ $ مضمنة $ h $ مضمنة من المجموعة الفرعية.

في الختام ، معلمات المجال لخوارزميات لدينا هي sextuplet$$ $ inline $ (p، a، b، G، n، h) $ inline $ .
مثل هذه المنحنيات الإهليلجية تعمل على المجال المحدود$$ $ inline $ \ mathbb {F} _p $ inline $ اين$$ $ inline $ p $ inline $ هو عدد أولي كبير إلى حد ما. لذلك لدينا مجموعة من الأعداد الصحيحة مودولو$$ $ inline $ p $ inline $ ، حيث العمليات ، مثل الجمع والطرح والضرب والعكس المضاف والعكس المضاعف ممكنة. تعمل الإضافة والضرب بشكل مشابه للحساب المعياري أو ما يسمى بحساب "الساعة" الذي رأيناه في "التفاف حول" RSA.
لأن المنحنى متماثل حول المحور السيني ، مع إعطاء أي نقطة$$ $ مضمنة $ P $ مضمنة ، يمكن أن نتخذها$$ $ inline $ −P $ inline $ أن تكون النقطة المقابلة لها. نحن نأخذ$$ $ inline $ −O $ inline $ أن تكون مجرد$$ $ مضمنة $ O $ مضمنة .
يتم تعريف إضافة نقاط منحنى بطريقة تعطى نقاط$$ $ مضمنة $ P $ مضمنة و$$ $ مضمنة $ Q $ مضمنة ، يمكننا رسم خط متقاطع مع كل من تلك النقاط ومنحنى متقاطع في نقطة ثالثة$$ $ مضمنة $ R $ مضمنة لذلك$$ $ inline $ P + Q = -R $ inline $ و$$ $ مضمنة $ P + Q + R = 0 $ مضمن $ .

دعونا نلقي نظرة على شرح مارك هيوز :

يظهر أعلاه خط منحدر ثابت يسير على طول سطح التوروس. يمر هذا الخط عبر نقطتين صحيحتين تم اختيارهما بشكل عشوائي على المنحنى.



لإضافة نقطتين على الرسم البياني ، ارسم خطًا من أول نقطة محددة$$ $ مضمنة $ P $ مضمنة إلى النقطة المحددة الثانية$$ $ مضمنة $ Q $ مضمنة ، وقم بتمديد الخط حتى يتقاطع مع نقطة أخرى على الرسم البياني$$ $ inline $ -R $ inline $ ، تمديده عبر حدود المؤامرة إذا لزم الأمر.

بمجرد اعتراض نقطة عدد صحيح ، قم بعكس النقطة رأسياً عبر منتصف الرسم البياني (خط منقط برتقالي) للعثور على نقطة جديدة$$ $ مضمنة $ R $ مضمنة على الرسم البياني. لذلك$$ $ inline $ P + Q = R $ inline $ .

الضرب من قبل العددية هو الآن تافهة:$$ $ inline $ n \ cdot P = P + P + P + \ dots + P $ inline $ (هنا هي$$ $ inline $ n $ inline $ summands).

تكمن وظيفة trapdoor هنا في مشكلة اللوغاريتم المنفصل (بالنسبة إلى المنحنيات الإهليلجية) ، وليس المشكلة التي أجريناها في قسم RSA. المشكلة هي: إذا كنا نعرف$$ $ مضمنة $ P $ مضمنة و$$ $ مضمنة $ Q $ مضمنة ما هذا$$ $ مضمنة $ k $ مضمنة ، هذا$$ $ inline $ Q = k \ cdot P $ inline $ ؟

من المفترض أن تكون كل من مشكلة التعمير (الكامنة وراء RSA) واللوغاريتم المنفصل للمنحنيات الإهليلجية (والتي هي أساس ECDSA و ECDH) صعبة ، أي أنه لا توجد خوارزميات معروفة لحل هذه المشكلة في وقت متعدد الحدود لمفتاح معين الطول.

بينما ، عادةً ما يكون من العار على مزج تبادل المفاتيح (ECDH) مع خوارزمية التوقيع (ECDSA) ، إلا أننا نحتاج إلى شرح كيفية عملهما معًا. تحتوي شهادة TLS الحديثة على مفتاح عمومي ، في حالتنا ، لزوج مفاتيح منحنٍ إهليلجي منحنٍ إهليلجي ، موقَّع عادةً بواسطة سلطة أعلى مستوى. يتحقق العميل من توقيع الخادم ويحصل على السر المشترك. يتم استخدام السر المشترك في خوارزمية تشفير متماثل ، مثل AES أو ChaCha20. ومع ذلك ، يظل المبدأ هو نفسه: الموافقة على معلمات المجال (sextuplet) ، والحصول على زوج المفاتيح ، حيث يكون المفتاح الخاص عددًا صحيحًا تم اختياره عشوائيًا (multiplicand من$$ $ inline $ Q = k \ cdot P $ inline $ ) ، والمفتاح العمومي هو نقطة في المنحنى. تستخدم خوارزميات التوقيع النقطة الأساسية$$ $ مضمنة $ g $ مضمنة ، وهو مولد لمجموعة فرعية من النظام الأساسي الكبير$$ $ inline $ n $ inline $ ، مثل هذا$$ $ inline $ n \ cdot G = 0 $ inline $ ، حيث 0 هو عنصر الهوية. يثبت التوقيع أنه يتم إنشاء اتصال آمن مع الطرف الأصلي - خادم يحمل شهادة TLS (المفتاح العمومي) موقعة من قبل بعض المرجع المصدق لاسم الخادم المحدد.

(EC) DH (E) + ECDSA = نموذج المصافحة الحالي

في TLS (1.3) الحديث ، يقوم العميل والخادم بإنشاء زوج مفاتيح عام-خاص على الطاير ، أثناء إنشاء الاتصال ، يطلق على هذا الإصدار Ephemeral من تبادل المفاتيح. تدعم مكتبات TLS الأكثر شيوعًا هذا المتصفح. معظمهم يستخدمون منحنى إهليلج إدوارد 25519 ، الذي قدمه دانيال جيه. بيرنشتاين (djb) ، ويوفر أمانًا 128 بت. منذ 2014 openssh يستخدم هذا المنحنى لإنشاء زوج المفاتيح. في عام 2019 ، لا تزال المتصفحات لا تدعم جلسات TLS مع وجود خوادم لديها شهادة مع المفتاح العام EdDSA.

ولكن دعنا نعود إلى كيفية عمل الأشياء في نهاية عام 2019 باستخدام TLS 1.3.

تقتصر آليات التبادل الرئيسية في TLS 1.3 على (EC) DH (E) المستندة إلى (مع x25519 هو واحد معتمد في مكتبات TLS من جانب العميل لمعظم المتصفحات الشعبية وكذلك مكتبات TLS من جانب الخادم ، مثل OpenSSL ، التي سنقوم بفحصها لاحقًا) ، وقائمة مجموعة التشفير تحتوي على ثلاث إدخالات فقط: TLS_AES_128_GCM_SHA256 و TLS_AES_256_GCM_SHA384 و TLS_CHACHA20_POLY1305_SHA256. لأولئك منكم الذين يدركون كيف تم تسمية أجنحة التشفير في إصدار TLS 1.2 ، من الواضح على الفور أن آلية تبادل المفاتيح أصبحت الآن "منفصلة" عن اسم مجموعة الشفرات ، وأيضًا تمت إزالة صيغ الصرف الثابتة RSA و Diffie - Hellman الثابتة من المواصفات تماما. حتى استئناف الجلسة بناءً على PSK يتم عبر ECDHE في TLS 1.3. كما أنه صحيح بالنسبة لمعلمات DH المخصصة ، والتي لا يُسمح بها الآن ، مما يترك فقط تلك المتفق عليها عمومًا لتكون آمنة في مواصفات البروتوكول النهائي.

من المثير للاهتمام أن هناك اختلافًا كبيرًا في كيفية عمل خوارزميات التشفير غير المتماثلة في الوقت الحاضر. باستخدام شهادات ECC (وشهادات ECDSA بشكل خاص) ، نستخدم مفاتيح أصغر للوصول إلى مستويات "ملائمة" من الأمان ، مقارنةً مع RSA. يتيح ذلك استخدام خوارزمية أقوى للتشفير غير المتماثل وآليات تبادل المفاتيح على الأجهزة الصغيرة وأحيانًا في الأشياء التي لا تعتبر عمومًا جهازًا (البطاقة الذكية).

بادئ ذي بدء ، من الضروري ذكر معنى "نظام التشفير المختلط" من حيث TLS 1.3.
نظام التشفير المختلط هو النظام الذي يستخدم تشفيرًا غير متماثل (المفتاح العمومي) لإنشاء سر مشترك ، يتم استخدامه أيضًا كمفتاح في دفق متماثل أو تشفير كتلة.

ثانيا ، البنية التحتية للمفتاح العام والشهادات. من المثير للاهتمام أن مارتن هيلمان في مقابلته عام 2004 ذكر "البطل المجهول" لورين كونفلدر ، التي قدمت أطروحة شهادة البكالوريوس في معهد ماساتشوستس للتكنولوجيا هيكل شجرة لما نعرفه الآن باسم البنية التحتية للمفتاح العام. ومع ذلك ، دعونا نعود إلى الشهادات.

يتم ضمان حقيقة أن الخادم لديه المفتاح الخاص من خلال توقيعه ، والذي يمكن التحقق منه باستخدام المفتاح العمومي للخادم. وتضمن الشهادة أن بعض المفتاح العمومي ينتمي إلى خادم معين. فهذا يعني أنك تقيم اتصالًا آمنًا مع الطرف المحدد وليس مع المحتال. البنك الذي تتعامل معه ، وليس مجرمي الإنترنت. يوجد في TLS 1.3 تحسن كبير مقارنة بتنسيق التفاوض السابق - حيث يقوم الخادم بتوقيع جميع المعلومات التي لديه حتى هذه اللحظة: مرحباً بالعميل ومرحباً للخادم ، بما في ذلك التشفير المتفاوض عليه. دعونا نلقي نظرة على القسم المقابل من RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

في TLS 1.3 العميل يرسل حصة المفتاح (جنبا إلى جنب مع المعلمات اللازمة) ، خوارزميات التوقيع على الفور في الرسالة الأولى (عميل مرحبا). يتم إنشاء المفاتيح اللازمة للتبادل مع الخادم في الخلفية ، دون أن يلاحظ المستخدم هذه الحقيقة. يتم تبادلهم بشكل إضافي مع الخادم لإنشاء سر شائع ، من المفاتيح السرية التمهيدية التي تم إنشاؤها عندما أرسل الخادم رسالته (Server Hello) للرد على العميل.
في جانب "Server Hello" ، يمكنك رؤية الشهادة * التي يتم نقلها إلى العميل ، جنبًا إلى جنب مع جزء التحقق من الشهادة * الذي يتحقق من امتلاك الطرف للمفتاح الخاص لإدخال المفتاح العمومي المقابل ، وإنشاء مفتاح جلسة (متماثل) إذا كل شيء يسير كما هو مخطط له - بمعنى ، أن الجانب الذي يطلب البيانات (العميل) قد تحقق بنجاح من جانب الرد (الخادم) ، مما خلق سرًا مشتركًا.

هناك عمليتان أساسيتان مخفيتان في عمليات النقل هذه - إنشاء التوقيع والتحقق من التوقيع. هذه مصنوعة على جانبي الاتصالات لأن "التوقيع" هو في الأساس دليل على أن الطرف لديه بالفعل المفتاح الخاص المطابق للمفتاح العمومي ، وأن البيانات تأتي من الموقّع وأن الرسالة لم يتم تغييرها أثناء النقل.

مع RSA ، كما سنرى لاحقًا ، فإن عملية التوقيع هي الأكثر تكلفة. نظرًا لأننا نوقع مع مفتاح 2048 أو 3072 بت ، فإن هذه العملية تقوم بتحميل الخادم بشكل كبير ، أكثر بكثير من تحميله العميل للتحقق من هذا التوقيع.

مع ECDSA ، لدينا مفاتيح أصغر (سننظر إلى ECDSA مع NIST P-256 (أو secp256v1)) ولكن عمليات أكثر تعقيدًا. ونتيجة لذلك ، يمكن اعتباره "RSA رأسًا على عقب" - حيث يتم تحميل العميل أكثر من خلال حساب التحقق من التوقيع ، بينما يتولى الخادم معالجة إنشاء التوقيع بسهولة. تتحقق القياسات من ذلك ، انظر قسم "A bit of standard".

يعمل هذا التأثير على زيادة حجم الإنترنت في الوقت الحاضر - حيث أن العملاء الحديثين يتمتعون بنفس القوة تقريبًا مثل الخوادم (مع الأخذ في الاعتبار فقط التردد الأساسي لوحدة المعالجة المركزية) ، حتى يتمكنوا من أخذ العملية الباهظة التكلفة على نحو فعال. يمكن للخادم ، بدوره ، استخدام القدرات المحررة لإنشاء المزيد من التواقيع وإنشاء المزيد من الجلسات.

دعونا تشفير توقيع الشهادة

لذلك ، من أجل تزويد القارئ ببعض الإرشادات العملية والسهلة حول كيفية إنشاء خادم يدعم بروتوكول TLS مع زوج مفاتيح ECDSA الموقّع من سلطة Let's Encrypt ، قررنا توضيح عملية كاملة لإنشاء زوج مفاتيح مطلوب لإنشاء CSR (طلب توقيع شهادة) لـ Let's Encrypt ، ونتيجة لذلك ، احصل على شهادة ECDSA اللازمة لخادمنا.

يتعين علينا إنشاء مفتاح خاص للمتابعة. سوف نستخدم مكتبة OpenSSL.
يصف دليل OpenSSL توليد أي مفاتيح EC من خلال أمر خاص ، مخصص بشكل خاص لفرع المنحنى الإهليلجي لخوارزمية التوليد.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

للتحقق من أن مكتبة OpenSSL قد فعلت كل شيء بشكل صحيح ، يمكننا تنفيذ الأمر ec .

 openssl ec -in privatekey.pem -noout -text 

سيُظهر لنا الإخراج المنحنى المحدد الذي تم إنشاء المفتاح به.

الخطوة التالية ضرورية جدًا لإنشاء CSR - من أجل تخطي عملية ملء جميع تفاصيل المعلومات اللازمة للحصول على الشهادة التي نحتاج إليها من ملف التكوين. لحسن الحظ ، أنجزت Mozilla العمل بكامله من خلال تقديم " SSL Configuration Generator ". هناك ، يمكنك الاختيار من بين أي خيارات خادم المتاحة. قد يبدو شكل OpenSSL النقي ، والذي لا يتواجد في صفحة المولد ، مثل هذا:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

ملاحظة: ليس من الضروري امتلاك CNF - إذا لم تقم بذلك ، فسيُطلب منك ملء هذه التفاصيل في سطر الأوامر.

الآن ، اتبع إنشاء المسؤولية الاجتماعية للشركات نفسها. هنا لدينا أمر OpenSSL مفيد.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

يمكننا أيضًا التحقق من صحة CSR المنشأة حديثًا.

 openssl req -in csr.pem -noout -text -verify 

لقد وصلنا إلى المرحلة النهائية - باستخدام عميل ACME ، certbot ، لتمرير طلب توقيع الشهادة الخاص بنا إلى Let's Encrypt.

يساعدك Certbot في الحصول على الشهادة المطلوبة ولديه مجموعة كبيرة من الخيارات. هنا ، إذا كنت جديدًا في تشفير المفتاح العام ، وبنية PKI الأساسية لدينا في عام 2019 ، فمن الأفضل استخدام --dry-run قبل محاولة الحصول على الشهادة لأي مجال من مجالاتك.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

في هذه الحالة ، يتحقق عميل certbot من أن قائمة المجالات المطلوبة (في سطر الأوامر) تتطابق مع المجالات المدرجة في طلب توقيع الشهادة. في الأمر --dns-somednsprovider يكمن قليلاً من الكذب ، لأن هناك الكثير من الطرق التي يمكنك بها إثبات "دعونا تشفير" أنك تمتلك جزءًا معينًا من حركة مرور الإنترنت. ومع ذلك ، إذا كنت تستخدم بعض مزودي خدمة الاستضافة السحابية العامة ، مثل DigitalOcean ، و Hetzner ، و Amazon ، و Azure ، وأي شيء - فمن المحتمل أن تكون هناك طريقة أكثر طبيعية لتوفير المعلومات المطلوبة ، لأن مزودك قد صنع بالفعل أداة تكامل.

بعد ذلك ، إذا كنت متأكدًا من صحة المعلمات التي تستخدمها في تمرير CSR الخاص بك إلى Let's Encrypt عبر عميل certbot - استبعد --dry-run من أمرك والمتابعة.

في حالة نجاحه ، سينتج العميل عدة شهادات كمخرجات: الشهادة الموقعة نفسها ، والجذر والوسائط الوسيطة ، والجمع بين الأخير كسلسلة شهادات تم تحديد اسمها الأخير ، وكل ذلك بتنسيق ملف .pem.

OpenSSL لديه أمر يمكننا استخدامه لفحص الشهادات:

 openssl x509 -in chainfilepath.pem -noout -text 

في هذه المرحلة ، أصبح من الواضح أن Let's Encrypt وقّع الشهادة باستخدام ملخص SHA256. بالإضافة إلى ذلك ، يقع توقيع ECDSA Root and Intermediates ضمن قسم "الميزات القادمة" ، مما يعني فعليًا أنه في الوقت الحالي ستحصل على وسيطة RSA فقط. لكن هذا جيد لأنك لا تزال تستخدم المفتاح العمومي ECDSA.

في نهاية هذا القسم ، نود أن نقول شيئًا فيما يتعلق بطول المفاتيح. في أمان المعلومات ، من الشائع أن نقول إن مستوى الأمان هو 2 ^ x ، حيث x هو طول البتة (RSA قليلاً من الاستثناء هنا ، لأنه ينمو أبطأ نوعًا ما من الأسي). لتقريب كيف تتوافق المفاتيح المستخدمة مع خوارزميات مختلفة مع بعضها البعض ، نشير إلى صفحة الويكي OpenSSL.
كما ترون ، فإن الاختلافات بارزة للغاية. على الرغم من أنه مع Let's Encrypt ، لم نتمكن من الحصول على أي شهادات موقعة خارج مفتاحي المنحنى الإهليلجي 256 (secp256v1) و 384 (secp384r1).

المشكلات المعروفة والاستثناءات ، و NSA

ائتمانات: xkcd

على الأرجح ، كانت المشكلة الرئيسية المتمثلة في استخدام تشفير المنحنى الإهليلجي على مر السنين هي الحاجة إلى مولد أرقام عشوائي مصنوع بعناية فائقة ، من أجل إنشاء مفاتيح لمستوى الأمان المطلوب.

كانت هناك فضيحة هائلة حول خوارزمية Dual_EC_DRBG (منحنى القطع العشوائي ذو المنحنى الإهليلجي المزدوج) ، والتي استغرقت سنوات عديدة لحلها. أيضا ، هناك عدم اليقين حول براءات الاختراع ECC ، لأنه من المعروف أن العديد منهم ينتمون إلى شركة Certicom ، التي اشترتها بلاك بيري. هناك أيضًا شركات معروفة بأنها معتمدة لاستخدام ECC من Blackberry. بالطبع ، هناك عدم ثقة بسيط في بعض معايير NIST ، والتي يمكن أو لا يمكن أن تتأثر وكالة الأمن القومي أو أي مؤسسة أخرى للإنفاذ والمراقبة بالولايات المتحدة.

جانب تنفيذ القضية هو سؤال مختلف تمامًا. في عام 2010 ، عانت وحدة التحكم في PlayStation 3 من استعادة Sony للمفاتيح الخاصة بسبب التنفيذ غير الصحيح لخوارزمية ECDSA - فقد كان لديها عشوائي ثابت جعل وظيفة trapdoor قابلة للحل. عانى OpenSSL أيضًا في السنة التالية ، ولكن سرعان ما حل مشكلة عدم الحصانة التي سمحت باستعادة مفتاح خاص بمساعدة هجوم توقيت ، لمزيد من المعلومات ، انظر إلى الورقة الأصلية .

في عام 2013 في مؤتمر RSA ، قدمت مجموعة من الباحثين " فشل عشوائيًا!" "ورقة حول نقاط الضعف في Java SecureRandom. بعد مرور نصف عام ، تم تحويلها إلى محافظ Android Bitcoin ، التي تم إنشاؤها باستخدام PRNG غير الآمن بشكل كافٍ.

نظرًا لوجود ثغرات أمنية خطيرة اكتشفتها ، في أغسطس 2013 نفسه ، أصدرت IETF RFC 6979 ، واصفًا الجيل الحاسم من k المستخدم في إنشاء المفاتيح. يمكننا أن نقول أن مثل هذا الإجراء قد حل المشكلة ، لكننا لن - في أي وقت يمكن أن يجد الباحثون مشاكل في تطبيقات عديدة بسبب الانحراف غير الضروري عن مواصفات البروتوكول.

حول وكالة الأمن القومي. إذا لم تكن قد سمعت عن قصة Dual_EC_DRBG - حجز بعض الوقت وقراءة المقالات ذات الصلة ، فلن نأسف للدخول في التفاصيل. إدوارد سنودن جزء من هذه القصة لأن كشوف 2013 أثبتت الشكوك السابقة. وقد أدى ذلك إلى فقدان العديد من مصممي التشفير البارزين ثقتهم في NIST لأن تلك المنظمة صممت ووصفت العديد من المنحنيات والخوارزميات الأخرى ، ECDSA.

يعد منحنى دانييل برنشتاين ووظيفة DH في الإجابة على هاتين المشكلتين ، وكما ذكرنا سابقًا ، فإن الانتقال نحو EdDSA يكون بطيئًا على الرغم من أنه واضح. حتى مع منحنيات NIST ، لم يتم العثور على دليل على ضعفها حتى الآن ، وكما ذكرنا سابقًا ، فإن التجربة ذات الصلة العشوائية كانت مفيدة للغاية.

في الختام ، نود أن نعطي اقتباس لجون فون نيومان: "كل من يحاول توليد أرقام عشوائية بوسائل حتمية ، بالطبع ، يعيش في حالة من الخطيئة".

قليلا من المعيار

استخدمنا خادم NGINX 1.16.0 مع OpenSSL 1.1.1d لتشغيل هذه المعايير مع شهادات مختلفة. كما ذكرنا سابقًا ، يتيح Let's Encrypt حاليًا فقط خوارزميات prem256v1 و secp384r1 لطلبات توقيع الشهادات ، ولا توفر شهادات ECDSA الجذر والوسيطة ، وربما نعمل في هذه الميزة في وقت كتابة هذه المقالة.
كما ترون ، بالنسبة للفرد الواحد من وحدة المعالجة المركزية Intel® Xeon® Silver 4114 @ 2.20 جيجاهرتز (التي تم إطلاقها في Q3'17) ، فإن الفرق الكلي في أداء ECDSA ، مقارنةً بـ RSA 2048 المعتمد على نطاق واسع هو 3.5x.

الآن دعونا نلقي نظرة على نتائج سرعة OpenSSL للمعالج نفسه مع ECDSA و RSA.
هنا يمكننا أن نرى تأكيدًا على الأطروحة السابقة للتكاليف الحسابية المختلفة للعلامة والتحقق من عمليات ECC و RSA. نتيجةً لذلك ، تم تزويد TLS 1.3 ECC حاليًا بدعم أداء كبير على مستوى أمان أعلى ، مقارنةً بـ RSA. هذا هو السبب الأكثر أهمية في قيامنا في Qrator Labs بتشجيع عملائنا على اعتماد ECDSA. مع وحدات المعالجة المركزية الحديثة ، يمكنك الحصول على الفرق تقريبًا 5x لصالح ECDSA.

إذا كنت مهتمًا بكيفية أداء وحدة المعالجة المركزية الخاصة بك لحسابات التشفير ، يمكنك تشغيل أمر بسيط openssl speed . -rsa -eddsa المعلمات -eddsa -ecdsa و -eddsa نتائج مرجعية لخوارزميات التوقيع المقابلة.

(تراكب) المستقبل

ائتمانات: djb

من المفارقات أنه بينما كنا نعد هذه المقالة ، أعلنت Google عن " بلوغ تفوق الكم ". هل هذا يعني أننا في خطر الآن وأن كل شيء تم تطويره حتى هذه اللحظة لا يوفر أي سرية؟

حسنا لا.

كما كتب Bruce Schneier في مقالته عن " التشفير والتشفير بعد أراضي الأجانب " IEEE Security and Privacy ، يمكن توجيه ضربة هائلة مع كمبيوتر كمي قوي بما فيه الكفاية إلى تشفير المفتاح العمومي (غير المتماثل). لا يزال التشفير المتماثل قويًا.

نريد أن نقتبس Bruce Schneier بما يلي:

هناك سيناريو مستقبلي آخر يجب مراعاته ، سيناريو لا يتطلب كمبيوترًا كميًا. في حين أن هناك العديد من النظريات الرياضية التي تدعم الاتجاه الواحد الذي نستخدمه في التشفير ، فإن إثبات صحة هذه النظريات هو في الواقع واحدة من أكبر المشاكل المفتوحة في علوم الكمبيوتر. كما أنه من الممكن لمكتشف تشفير ذكي العثور على خدعة جديدة تسهل كسر خوارزمية معينة ، فقد نتخيل الأجانب بنظرية رياضية كافية لكسر جميع خوارزميات التشفير. بالنسبة لنا ، اليوم ، هذا سخيف. تشفير المفتاح العام هو كل نظرية الأعداد ، ومن المحتمل أن تكون عرضة للأجانب الأكثر ميلًا رياضيًا. تشفير متماثل هو الكثير من التشويش غير الخطي ، من السهل جدًا جعله أكثر تعقيدًا ، ومن السهل زيادة طول المفتاح ، بحيث لا يمكن تصور هذا المستقبل. النظر في متغير AES مع كتلة 512 بت وحجم المفتاح ، و 128 طلقة. ما لم تكن الرياضيات مختلفة اختلافًا جوهريًا عن فهمنا الحالي ، فستكون آمنة حتى يتم تصنيع أجهزة الكمبيوتر من شيء آخر غير المادة وتحتل شيئًا آخر غير الفضاء.

ولكن في حالة حدوث ما لا يمكن تصوره ، فإن ذلك سيترك لنا تشفيرًا قائمًا على نظرية المعلومات فقط: منصات لمرة واحدة ومتغيراتها.

هذا هو المجال الذي توجد فيه معظم المشكلات ، باستثناء البحث عن عيوب التنفيذ. إذا كانت هناك مجموعة من علماء الرياضيات الممولين تمويلًا جيدًا ومحللي التشفير / التشفير ومهندسي الكمبيوتر يعملون على إثبات أو دحض بعض المشكلات الرياضية المعقدة غير العادية (مثل P؟ = NP) وتحقيق نتائج جوهرية حتى هذه اللحظة ، فقد نكون في مأزق. ومع ذلك ، فمن غير المرجح إخفاء هذه التطورات في نظريات علوم الكمبيوتر والمعلومات وقابلية الحسابية ، حيث أن هذه الحقيقة ستكتب أسماء منشئيها على صفحات التاريخ ، وعلى وجه التحديد ، كتب تاريخ الإنترنت ، والتي لا تقدر بثمن لأي شخص ذكي. . لذلك ، يمكن اعتبار مثل هذا السيناريو مستحيلًا تقريبًا.

ليس من الواضح ، ما إذا كانت ستحقق أي نجاحات في الحوسبة الكمومية في أقرب 5 سنوات ، على الرغم من أن هناك بالفعل عدة بدائل للتشفير تُعتبر مناسبة لعالم ما بعد الكم: المشابك ، المنحنى الإهليلجي الفائق الإيزوجيني ، والتجزئة والرموز. في الوقت الحالي ، يقوم المتخصصون في مجال الأمن بالتجربة معهم. ومع ذلك ، ليس هناك شك في أنه في حالة الحاجة ، ستوظف البشرية بسرعة مثل هذه الخوارزميات على نطاق واسع.

في الوقت الحالي ، يبدو أن التشفير القائم على المنحنى الإهليلجي مناسب تمامًا للعقد المستقبلي ، مما يوفر الأمان والأداء.