👉🏼 👰🏽 💪🏼 كيف يعمل تشفير المنحنى الإهليلجي في TLS 1.3 💅 🏒 🐵

تحذيران للقارئ:

من أجل (قدر الإمكان) تبسيط عملية التفسير والضغط على حجم المنشور ، من المفيد إجراء حجز رئيسي على الفور - كل شيء نكتبه عن الجانب العملي للمشكلة هو الصحيح لإصدار بروتوكول TLS 1.3. هذا يعني أنه على الرغم من أن شهادة ECDSA ستعمل ، إذا رغبت في ذلك ، مع TLS 1.2 ، فقد تم وصف عملية المصافحة وأجنحة التشفير والمعايير بناءً على أحدث إصدار من بروتوكول TLS - 1.3. كما تعلم ، هذا لا ينطبق على الوصف الرياضي للخوارزميات التي تقوم عليها أساس أنظمة التشفير الحديثة.

لم يتم كتابة هذه المادة بواسطة عالم رياضيات أو حتى مهندس - على الرغم من أنها ساعدت في تمهيد الطريق عبر الغابة الرياضية. شكرا جزيلا لموظفي Qrator Labs.

( E lliptic C urve) D iffie- H ellman ( E phemeral)

21st القرن ديفي هيلمان ليجاسي

بطبيعة الحال ، لا يبدأ هذا الموضوع مع ويتفيلد ديفي وليس مع مارتن هيلمان. ساهم آلان تورينج وكلود شانون مساهمة كبيرة في نظرية الخوارزميات ونظرية المعلومات ، وكذلك في مجال تحليل الشفرات. يعترف مؤلفو فكرة Diffie and Hellman بدورهما رسميًا بفكرة تشفير المفتاح العام (وتسمى أيضًا غير المتماثلة) - على الرغم من أنه من المعروف الآن أن نتائج جدية في هذا المجال قد تحققت أيضًا في المملكة المتحدة. ومع ذلك ، ظلوا سرا لفترة طويلة - مما يجعل السادة اثنين المذكورة في رواد الترجمة.

ما بالضبط؟

قد يبدو هذا أمرًا مضحكًا ، لكن حتى 6 نوفمبر 1976 ، لم تكن هناك معرفة متاحة بشأن أنظمة تشفير المفتاح العام. كان وايتفيلد ديفي ومارتن هيلمان (وفي الواقع رالف ميركل) - علماء الرياضيات ومهندسي الكمبيوتر وهواة ، وكذلك علماء التشفير أول من اقترح مفهومًا مناسبًا.

خلال الحرب العالمية الثانية ، ساعد التشفير في الحفاظ على سرية المعلومات ، وساعد تحليل التشفير في الكشف عنها. تعتبر الولايات المتحدة والمملكة المتحدة نفسيهما الأكثر تقدماً في مجال التشفير. تضمن هذان البلدان خوارزميات تشفير في قسم الأسلحة واعترضا على حق صادراتهما. في الوقت نفسه ، تم تخفيف التشفير المتاح والمخصص للاستخدام التجاري أو المنزلي في هذه البلدان. لهذا السبب ، لم يتم الاعتراف بالباحثين البريطانيين الذين يعملون على مخطط توزيع مفاتيح غير متماثل في مركز الاتصالات الحكومية (GCHQ) وتطوير مفهوم مماثل من قبل المجتمع حتى عام 1997 ، عندما فقدت القيود الحالية على خوارزميات التشفير ووصفها كل معنى ، وبشكل عام عفا عليها الزمن أخلاقيا.

بالعودة إلى زوجنا من المخترعين - ماذا بالضبط ثورة ديفي وهيلمان؟

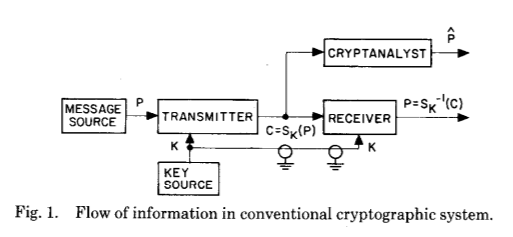
لشرح ذلك ، دعونا نلقي نظرة على الرسم التوضيحي من المنشور الأصلي ، والذي يعكس تمامًا قفزة عملاقة في فهم كيفية عمل التشفير - حتى لو كان مبدئيًا فقط نظريًا:

والآن لما يلي:

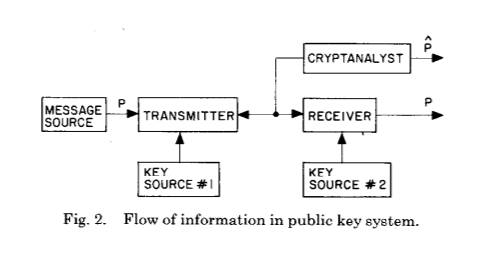
تُظهر هاتان الصورتان الابتكار الرئيسي لـ Whitfield Diffie و Martin Hellman بعد قرون من تطور التشفير وتحليل الشفرات - وهو إنشاء سر شائع نتيجة لحسابات من نوع معين.

دعونا نلقي نظرة على صورة أخرى من ويكيبيديا ، حيث يتم استخدام ألوان مختلفة كأسرار:

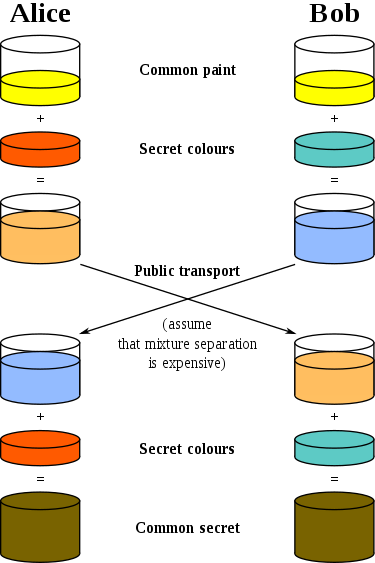
كما تشرح جيدًا ما يحدث. قبل ابتكار Diffie و Hellman ، كان هناك مفتاح مشترك واحد فقط في شكل مخطط إنشاء مفتاح مشترك - تم استخدامه لتشفير رسالة وفك تشفيرها. إذا كنت تريد نقل هذا المفتاح إلى الجانب الثاني ، فيجب إرساله عبر القناة المحمية أصلاً. تصبح جميع القيود المفروضة على هذا المخطط واضحة فورًا - فأنت بحاجة إلى قناة اتصال آمنة (من الاستماع) ، ولا يمكنك استخدام نفس المفتاح أكثر من مرة ، ومن الناحية المثالية ، يجب أن يتوافق طول المفتاح مع طول الرسالة.

أثبت كلود شانون ، في عمله اللاحق عن رفع السرية ، "نظرية الاتصال في الأنظمة السرية" ، أن جميع الأصفار غير القابلة للكسر نظريًا يجب أن يكون لها نفس خصائص كتلة تشفير لمرة واحدة - تُعرف أيضًا باسم تشفير Vernam ، باسم مُصمم هذه الخوارزمية لتشفير الدفق المتعدد الأقطاب.

ومرة أخرى ، دعونا نلقي نظرة على المنشور العلمي الأصلي:

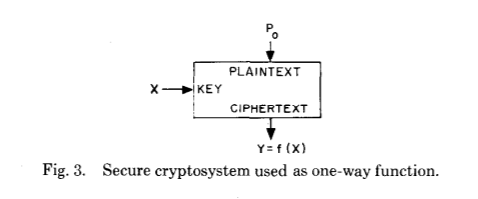
قبل أن نذهب إلى أبعد من ذلك ، دعونا نسأل أنفسنا سؤالًا بسيطًا وواضحًا - كيف يمكن لشخصين ، حتى المتقدمين في التفكير الفكري ، أن يتوصلوا إلى شيء مذهل في المجال التطبيقي ، خاصة بالنظر إلى النجاحات الهائلة التي حققتها الحرب؟ على الأرجح بسبب مزيج من المجالات التالية التي كانت تتطور بنشاط بعد ذلك:

نظرية المعلومات التي صاغها كلود شانون ؛
نظرية الخوارزمية ، التي تأثرت ، من بين أمور أخرى ، بآلية ألونزو ، جون فون نيومان وآلان تورينج ؛
والأهم من ذلك كله ، نظرية الحوسبة ، القائمة بشكل رئيسي على عمل تورينج.

يمكننا القول أن كل هذه المناطق تطورت ونضجت في نفس الفترة من القرن العشرين. كما ذكر ديفي وهيلمان كلود شانون كشخصية أثرت في عملهم أكثر من غيرهم.

يوضح مفهوم "الأمن العالمي" بقلم آرين لينسترا مقدار الطاقة التي يجب إنفاقها على "اختراق" نظام تشفير متماثل مع مفاتيح بأطوال مختلفة. اتضح أنه لكسر المفتاح 228 بت للخوارزمية المبنية على منحنيات إهليلجية ، فإنك تحتاج إلى قدر من الطاقة يكفي لتسخين كل الماء على الأرض حتى نقطة الغليان. ومع ذلك ، لا يكون هذا البيان صحيحًا إلا إذا أخذنا في الاعتبار الخوارزميات المعروفة واستخدمنا المعدات الحديثة ، نظرًا لأنه من الممكن أن تكون الخوارزميات أو المعدات الأكثر كفاءة ممكنة ، ولكن وجودها غير معروف بعد. يشبه المفتاح 228 بت لخوارزمية EC للتطفل على التعقيد مفتاح 2380 بت في RSA ، لكن المزيد حول ذلك لاحقًا. في هذه المقارنة ، يتم استخدام مفاتيح RSA و EC في نظام تشفير غير متماثل ، ويمكن اعتبارهما مكافئين لمفتاح 128 بت في مخطط متماثل.

من السهل أن نتخيل أن شيئًا ما "يصعب حسابه" سيتطلب قدراً كبيراً من الوقت والطاقة لحسابه. نميل إلى الاعتقاد بأن أجهزة الكمبيوتر يمكنها "حساب أي شيء" ، لكن اتضح أن هذا بعيد عن الحقيقة.

أولاً ، هناك أمثلة للمشكلات غير القابلة للحل ، مثل مشكلة التوقف. ومع ذلك ، في مجال التشفير لا تستخدم هذه المهام.

ثانياً ، إذا أخذنا في الاعتبار وقت التشغيل الذي تتطلبه خوارزمية معينة ، فيمكن أن يكون كبيرًا بشكل تعسفي. هذا هو بالضبط ما يستخدم التشفير. تُعتبر المهمة "بسيطة" من الناحية الحسابية إذا كان الوقت اللازم للخوارزمية المقابلة للعمل يعتمد على حجم بيانات المدخلات (المقاسة بالبتات) باعتباره متعدد الحدود:

T (n) = O (n^{k})

$T (n) = O (n ^ k)$ لبعض إيجابية

ك

$ك$ . في نظرية التعقيد الحسابي ، تشكل هذه المشكلات فئة التعقيد P. إذا كان وقت تشغيل الخوارزمية ينمو بوتيرة أسرع من كثير الحدود ، على سبيل المثال ، أضعافا مضاعفة ، فإن هذه المهمة تعتبر "صعبة" حسابيا.

تتضمن فئة التعقيد P المهام التي توجد لها خوارزمية حتمية تعمل في كثير الحدود. فئة التعقيد الأخرى هي NP (التي ، من المفترض أن توجد مشاكل "صعبة") ، وهي مشكلة قابلية للحل - أي ، مشكلة تتطلب إجابة "نعم" أو "لا" ، يمكن التحقق من صحة الحل - أي لإثبات صحة الحل - في كثير الحدود الوقت. انظر كلمة "دليل" هنا؟ هذا هو المكان الذي ننتقل فيه إلى الوظائف أحادية الجانب التي تنتمي مشكلة الانقلاب إلى فئة التعقيد NP.

بواسطة: xkcd

(وظائف أحادية الاتجاه (مع إدخال سري))

بحكم التعريف ، فإن الوظيفة أحادية الاتجاه هي وظيفة يسهل حسابها لأي إدخال ، ولكن يصعب قلبها ، أي الحصول على الإدخال الأصلي بالنتيجة فقط. تشير كلمة "سهل" و "صعب" إلى نظرية التعقيد الحسابي المذكور أعلاه. ومن المثير للاهتمام أن وجود وظائف في اتجاه واحد (رياضيا) لم يثبت ، لأن دليلا قويا على وجودها من شأنه أن يثبت أيضا عدم المساواة بين الفئتين P و NP ، واحدة من مشاكل الألفية والمشكلة المفتوحة الملحة ، التي يعد حلها بحدوث انفراج حسابي. لذلك ، من الضروري أن تضع في اعتبارك أن معظم التشفير الحديث يعتمد على فرضيات غير مثبتة.

في المنشور الأصلي ، يقدم Diffie و Hellman جيلًا جديدًا من الوظائف أحادية الاتجاه ، ويطلقان عليهما "وظائف أحادية الاتجاه مع إدخال سري" - في وظيفة trapdoor الإنجليزية. كيف تختلف عن وظائف أحادية الاتجاه؟

دعنا ننظر إلى شرحهم الأصلي:

في نظام تشفير به مفتاح عمومي ، يتم إجراء التشفير وفك التشفير بواسطة مفاتيح مختلفة - E و D ، على التوالي ، بحيث يكون الحوسبة D من E مستحيلة عملياً (على سبيل المثال ، تتطلب $10 ^ {100}$ تعليمات). يمكن الكشف عن مفتاح التشفير E علنًا دون المساس بالمفتاح D. وهذا يسمح لأي مستخدم للنظام بإرسال رسالة إلى أي مستخدم آخر ، مشفرة بطريقة لا يمكن إلا لفك تشفيرها للمستلم المتوقع. <...> مهمة المصادقة ، ربما ، هي مشكلة اتصالات أكثر خطورة بالنسبة للمعاملات التجارية ، مقارنةً بتوزيع المفاتيح ، لأنها (المصادقة) تكمن في قلب أي نظام يعمل مع العقود وفواتير الدفع.

عادة ، يتم استخدام أحرف التشفير Alice و Bob لشرح مبادئ تشغيل نظام التشفير (يسعيان لتحقيق اتصال آمن). يوافق أليس وبوب على اختيار أعداد كبيرة

ن

$ن$ و

g

$g$ مثل هذا

1 < g < n

$1 <g <n$ . يؤثر هذا الاختيار على أمان الدائرة بأكملها. عدد

ن

$ن$ دعا وحدة يجب أن تكون بسيطة. علاوة على ذلك ، الرقم

(ن - 1) / 2 د و ل ا

$(ن -1) / 2 دولا$ يجب أن تكون بسيطة ، ولكن

g

$g$ يجب أن يكون الجذر البدائي في مجموعة المخلفات modulo

ن

$ن$ . بالإضافة إلى ذلك

ن

$ن$ يجب أن تكون كبيرة بما يكفي - ما لا يقل عن 512 بت في التمثيل الثنائي. علاوة على ذلك ، يمكن وصف بروتوكول Diffie-Hellman في خمس خطوات بسيطة:

أليس يختار $x$ (رئيس الوزراء الكبير) ويحسب $X = g ^ x \ bmod n$
يختار بوب $ذ$ (أيضا رئيس الوزراء كبير) ويحسب $Y = g ^ y \ bmod n$
أليس يرسل $X$ بوب ، بوب يرسل $Y$ أليس ( $x$ و $ذ$ كل منهم يبقى سرا)
أليس تحسب $k = Y ^ x \ bmod n$
بوب يحسب $k '= X ^ y \ bmod n$

نتيجة لذلك ، حصلت أليس وبوب على نفس النتيجة في البناء.

ك = ك^{'}

$ك = ك '$ - سر مشترك.

لذلك ، فإن الوظيفة أحادية الاتجاه مع إدخال سري هي وظيفة أحادية الاتجاه يمكن عكسها عن طريق الحصول على جزء من المعلومات الخاصة تسمى "الإدخال السري". يبدو الأمر بسيطًا ، ولكن في الممارسة العملية ، تبين أن العثور على مثل هذه الوظيفة ليس مهمة تافهة - فقد تبين أن أول وسيلة لائقة هي السلف لعائلة بأكملها من الخوارزميات تعتمد على مفتاح عمومي يسمى RSA بأسماء المبدعين: Ron Rivesta و Adi Shamira و Leonard Adleman.

RSA

في RSA ، يعتمد تعقيد عكس وظيفة على حقيقة أن التخصيص (عامل عدد) يستغرق وقتًا أطول بكثير من الضرب ، أو بشكل أكثر دقة ، يمكن القول أنه لم يتم العثور على طريقة لعامل الأعداد الكبيرة في وقت متعدد الحدود على جهاز كمبيوتر تقليدي ، على الرغم من أنه لم يكن ثبت أن مثل هذه الخوارزمية لا يمكن أن توجد.

في RSA ، كما هو الحال في أي نظام تشفير آخر به مفتاح عمومي ، يوجد مفتاحان: عام وخاص. تأخذ خوارزمية RSA رسالة إدخال ممثلة بسلسلة بت وتطبق عملية رياضية عليها (ترفع إلى معامل طاقة عددًا كبيرًا) للحصول على نتيجة يتعذر تمييزها من عشوائي. بالنسبة لفك التشفير ، يتم أخذ النتيجة ويتم تنفيذ عملية مماثلة لاستلام الرسالة الأصلية. في التشفير غير المتماثل ، يتم التشفير باستخدام مفتاح عام ، وفك التشفير باستخدام مفتاح خاص.

كيف هذا ممكن؟ بسبب حقيقة أن القيم المستخدمة تنتمي إلى مجموعة دورية محدودة (مجموعة الأعداد الصحيحة مع الضرب في الحساب المعياري). لا تعمل أجهزة الكمبيوتر بشكل جيد مع وجود أعداد كبيرة بشكل تعسفي ، ولكن خاصية المجموعة الدورية هي "التفاف" - عدد أكبر من الحد الأقصى المسموح به هو "لف" إلى قيمة من المجموعة المسموح بها. هذا يسمح لنا باستخدام مفاتيح بطول "لا يزيد عن" عدد معين من البتات. في التشفير القائم على المنحنيات الإهليلجية ، تُستخدم المجموعات الدورية (المضاعفة) أيضًا ، ولكن يتم إنشاؤها بطريقة مختلفة قليلاً ، كما سنرى لاحقًا.

على مستوى بدائي للغاية ، كل RSA تفعل هو اتخاذ اثنين من الأعداد الأولية الكبيرة ، ضربهم للحصول على ما يسمى الوحدة النمطية. يجب أن تكون جميع الأرقام الأخرى التي سيتم تنفيذ العمليات بها بين صفر وقيمة الوحدة. ستصبح الوحدة النمطية نفسها جزءًا من المفتاح العمومي - يحدد طولها طول المفتاح. الجزء الثاني من المفتاح العمومي هو الرقم الذي يتم اختياره بين صفر وقيمة وظيفة Euler (تستخدم تطبيقات RSA الحديثة وظيفة Carmichael بدلاً من Euler) من الوحدة النمطية ، مع بعض القيود الإضافية. أخيرًا ، يمكنك حساب المفتاح الخاص عن طريق حل المعادلة المعيارية. لتشفير الرسالة ، نأخذ الرقم الذي يمثل الرسالة ونرفعها ببساطة إلى القوة المساوية لقيمة المفتاح العام ، ونفك تشفيرها - لتلقي الرسالة الأصلية ، ونرفعها إلى القوة المساوية لقيمة المفتاح الخاص. نظرًا للطبيعة الدورية للمجموعة ، نحصل على نفس المعنى.

اليوم ، لدى RSA مشكلتان رئيسيتان ، إحداهما ناتجة عن الأخرى. مع نمو طول المفتاح ، لا ينمو التعقيد بالسرعة التي نرغب فيها. هذا بسبب وجود خوارزمية التعمير دون المستوى (ولكن لا يزال فائق الحدة ). لذلك ، من أجل الحفاظ على مستوى الحماية الضروري ، يجب أن ينمو طول مفتاح RSA بشكل أسرع من طول مفتاح ECC. لهذا السبب ، تعد أطوال مفاتيح RSA الأكثر شيوعًا اليوم كبيرة جدًا: 2048 و 3072 بت.

بعد قليل سنرى على أرقام محددة كيف يؤثر طول المفتاح على الأداء النهائي لنظام التشفير عن طريق مقارنة الشهادات الموقعة من قِبل Let's Encrypt RSA و ECDSA.

E lliptic C يحث Digital S اشتعال الخوارزميات

بحثًا عن وظائف أكثر موثوقية باستخدام إدخال سري ، في منتصف الثمانينيات استخدم مصففي التشفير فرعًا من الرياضيات مخصص لمنحنيات إهليلجية.

سيكون من الصعب للغاية وصف جميع تفاصيل التشفير بناءً على المنحنيات الإهليلجية في نص واحد ، لذلك لن نقوم بذلك. بدلاً من ذلك ، دعونا نلقي نظرة على وظيفة إدخال سرّية أحادية الاتجاه مبنية على أساس المنحنيات الإهليلجية ومشكلة اللوغاريتم المنفصلة.

هناك عدد كبير من مواد المراجعة ومقدمات أكثر تفصيلاً لهذا المجال من التشفير. نود أن نشير إلى "ECC: مقدمة لطيفة" من تأليف Andrea Corbellini ، خاصة إذا كنت مهتمًا بالجهاز.

نحن ، في هذه المادة ، مهتمون بتفسير أكثر بساطة بكثير.
يتم تعريف المنحنى الإهليلجي بمعادلة تبدو كما يلي:

y^{2} = x^{3} + a x + b

$y ^ 2 = x ^ 3 + ax + b$ .

الكائن الثاني هو مجموعة فرعية دورية على حقل محدود. يتم استخدام المعلمات التالية في خوارزمية ECC:

عدد أولي $ع$ ، الذي يحدد البعد من الحقل النهائي ؛
معاملات $دولا$ و $ب$ معادلات منحنى إهليلجي.
نقطة الأساس $G$ توليد المجموعة الفرعية التي سبق ذكرها ؛
ترتيب $ن$ مجموعات فرعية.
العامل المساعد $ح$ مجموعات فرعية.

نتيجة لذلك ، يتم تمثيل مجموعة المعلمات لخوارزميات لدينا ستة

$(p ، a ، b ، G ، n ، h)$ .

نقاط منحنى إهليلجي تنتمي إلى حقل محدود

m a t h b b F_{p}

$\ mathbb {F} _p$ حيث

ع

$ع$ هذا هو عدد أولي كبير إلى حد ما. لذلك ، لدينا العديد من الأعداد الصحيحة modulo

ع

$ع$ حيث عمليات مثل الجمع والطرح والضرب وأخذ العكس ممكنة. تعمل الإضافة والضرب بطريقة مماثلة لكيفية وصفنا هذا من حيث الحساب المعياري لقسم RSA (الالتفافي).

بما أن المنحنى متماثل حول المحور س ، لأي نقطة

P

$P$ يمكن أن نتخذها

- P

$−P$ والحصول على نقطة عكس ذلك. نحن على الفور تنص على أن هذه النقطة

$ O

$$O$ يتوافق مع الصفر ، أي

$ O

$$O$ سوف تكون بسيطة

ي ا د و ل ا

$يا دولا$ .

يتم تعريف إضافة نقاط على منحنى بحيث ، معرفة النقاط

P

$P$ و

ف د و ل ا

$ف دولا$ ، يمكننا رسم خط يمر عبر كل من هذه النقاط ، وكذلك الثالث -

R

$R$ لذلك

P + Q = - R

$P + Q = -R$ و

P + Q + R = 0

$P + Q + R = 0$ .

دعونا نلقي نظرة على التوضيح المصور لمارك هيوز :

نرى خطًا مستقيمًا ممتدًا على طول سطح التوروس. يتقاطع الخط مع نقطتين تم اختيارهما بشكل عشوائي على المنحنى.

من أجل العثور عليها $R$ ، نرسم خطًا من أول نقطة محددة $P$ إلى الثانية $ف دولا$ مواصلة الخط حتى يعبر المنحنى عند النقطة الثالثة $-R$ .

بعد التقاطع ، عكس النقطة بالنسبة لمحور الإحداثي من أجل العثور على النقطة $R$ .

يتم تحديد الضرب بواسطة العددية بوضوح تام:

n c d o t P = P + P + P + d o t s + P

$n \ cdot P = P + P + P + \ dots + P$ .

تعتمد الوظيفة أحادية الاتجاه مع إدخال سري في هذه الحالة على مشكلة اللوغاريتم المنفصلة في المنحنيات الإهليلجية ، وليس على التخصيص ، كما هو الحال مع RSA. يتم صياغة مشكلة لوغاريتم منفصلة في هذه الحالة على النحو التالي: إذا كانت معروفة

P

$P$ و

ف د و ل ا

$ف دولا$ ، ثم كيف تجد

ك

$ك$ مثل هذا

Q = k c d o t P

$Q = k \ cdot P$ ؟

تعتبر كل من مشكلة التعميق (الكامنة وراء RSA) واللوغاريتم المنفصل للمنحنيات الإهليلجية (والتي تشكل أساس ECDSA و ECDH) صعبة - بمعنى آخر ، لا توجد خوارزميات لحل هذه المشكلات في وقت متعدد الحدود لطول مفتاح معين.

على الرغم من أنني عادة ما يتم قصفي بخرق متسخ (في أحسن الأحوال) لمزج خوارزميات توزيع التوقيع (ECDH) مع التوقيع (ECDSA) ، لا يزال يتعين عليّ شرح كيفية عملهم معًا.تحتوي شهادة TLS الحديثة على مفتاح عمومي ، في حالتنا ، من زوج تم إنشاؤه باستخدام خوارزمية تستند إلى منحنيات إهليلجية ، موقعة عادةً من قبل بعض المنظمات الموثوقة. يتحقق العميل من توقيع الخادم وينشئ سرًا مشتركًا. يستخدم هذا السر في خوارزمية تشفير متماثل مثل AES أو ChaCha20. ومع ذلك ، تظل المبادئ الأساسية كما هي: الاتفاق على مجموعة (ستة) من المعلمات ، والحصول على زوج مفاتيح ، حيث يكون المفتاح الخاص عددًا صحيحًا تم اختياره عشوائيًا (عامل

) ، والمفتاح العمومي هو نقطة على المنحنى. خوارزميات التوقيع استخدم نقطة أساس

Q = k \cdot P

$Q=k\cdot P$

، وهو مولد لمجموعة فرعية من النظام

G

$G$

n

$n$ (

رئيس الوزراء كبير) ، لذلك

n

$n$

، حيث 0 هي العنصر المحايد للمجموعة. يثبت التوقيع أنه يتم إنشاء اتصال آمن مع جهة مصادقة - خادم له شهادة TLS (مفتاح عمومي) موقعة من قبل مؤسسة موثوقة لاسم خادم محدد.

n \cdot G = 0

$n\cdot G=0$

(EC) DH (E) + ECDSA = الشكل الحديث للمصافحة

في الإصدار 1.3 من بروتوكول TLS الحديث ، يقوم العميل والخادم بإنشاء زوج مفاتيح سريعًا ، مما ينشئ اتصالًا. يُطلق على هذا الإصدار "المؤقت" لخوارزمية تبادل المفاتيح. تدعم مكتبات TLS الأكثر شيوعًا مثل هذا البروتوكول. بالنسبة للجزء الأكبر ، يتم استخدام المنحنى الإهليلجي إدواردز 25519 ، الذي اقترحه دانيال بيرنشتاين جونيور (djb) ، والذي يوفر مستوى حماية 128 بت ، اليوم . منذ عام 2014 ، أصبح هذا المنحنى متاحًا لإنشاء أزواج المفاتيح في مكتبة opensh. ومع ذلك ، اعتبارًا من نهاية 2019 ، لا تزال المتصفحات لا تنشئ جلسة TLS مع الخوادم التي تستخدم المفتاح العمومي لخوارزمية توقيع EdDSA.

دعونا ننظر في كيفية عمل كل شيء في TLS 1.3.

في أحدث إصدار من البروتوكول ، تقتصر آليات توزيع المفاتيح على (EC) DH (E) - x25519 هي الوظيفة الأكثر شيوعًا للحصول على مفتاح مشترك - وهو مدعوم من قبل معظم مكتبات TLS الخاصة بالمستعرض والخوادم. تتكون مجموعة التشفير من ثلاثة إدخالات فقط: TLS_AES_128_GCM_SHA256 و TLS_AES_256_GCM_SHA384 و TLS_CHACHA20_POLY1305_SHA256. بالنسبة لأولئك الذين هم على دراية بكيفية تسمية مجموعات التشفير في الإصدار السابق من البروتوكول - TLS 1.2 ، من الواضح أن مؤشر آلية تبادل المفاتيح قد تم "فصله" عن مجموعة التشفير أثناء الانتقال إلى TLS 1.3. أيضًا ، تم إبعاد طرق تبادل المفتاح RSA و DH الثابتة عن المواصفات. حتى استرجاع الجلسة في TLS 1.3 بمساعدة PSK وتذاكر الجلسة السابقة تتم وفقًا لبروتوكول ECDHE ، حيث تكون آخر رسالة إلكترونية مهمة بشكل خاص.أيضًا ، في TLS 1.3 ، لا يمكن تعيين قيمك الخاصة لآلية Diffie-Hellman - لم يتبق سوى مجموعة محددة مسبقًا في مواصفات البروتوكول ، هناك إجماع بشأن أمان هذه المجموعة.

أهمية خاصة هو حقيقة أن آليات التشفير غير المتماثلة الحديثة تعمل بشكل مختلف. في ECC (على وجه الخصوص ، عند استخدام شهادات ECDSA) ، نستخدم مفاتيح ذات طول قصير نسبيًا مقارنة بـ RSA للوصول إلى مستويات أمان مقبولة. يتيح لك هذا استخدام أنظمة تشفير وتبادل مفاتيح قوية غير متماثلة حتى على الأجهزة التي ، على ما يبدو ، لا ينبغي أن يكون لديها طاقة كافية للعمليات الضرورية - على سبيل المثال ، البطاقات الذكية.

أولاً ، من الضروري توضيح معنى مصطلح "نظام التشفير المختلط" لأنه ينطبق على وصف TLS 1.3. يستخدم نظام التشفير المختلط نظام تشفير غير متماثل (مع مفتاح عمومي) لتأسيس سر مشترك ، والذي يستخدم بعد ذلك كمفتاح في خوارزمية تشفير كتلة أو دفق تشفير.

ثانياً ، هناك بنية أساسية للمفاتيح العامة (PKI) وشهادات (CA). من المثير للاهتمام أن مارتن هيلمان ذكر في عام 2004 أحد "الأبطال المجهولين" - لورين كونفيلدر ، الذي كانت أطروحته للدفاع عن دبلوم البكالوريوس في معهد ماساتشوستس للتكنولوجيا هي إمكانية إنشاء هيكل شجرة - ما نعرفه اليوم باسم PKI. ولكن دعنا نعود إلى الشهادات.

يتم التحقق من حقيقة أن الخادم يملك حقًا المفتاح الخاص من خلال توقيعه ، والذي يمكن التحقق منه باستخدام المفتاح العمومي. ويؤكد ملف الشهادة على الخادم أن مفتاح عمومي معين ينتمي إلى خادم معين. هذا يعني أنك تنشئ اتصالًا آمنًا مع المحاور المرغوب فيه ، وليس المحتال - البنك الذي تتعامل معه ، وليس الاحتيال عبر الإنترنت.

قام TLS 1.3 بتحسين نظام التفاوض بشكل ملحوظ مقارنة بالإصدارات السابقة من البروتوكول. يقوم الخادم الآن بتوقيع جميع المعلومات التي تم تلقيها في المصافحة في وقت إنشاء مثل هذا التوقيع: مرحبًا بالعميل ومرحب الخادم الخاص به ، إلى جانب مجموعة من الأصفار المحددة للاستخدام. دعونا نلقي نظرة على القسم المقابل من وصف التفاعل من RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data]

في TLS 1.3 ، يرسل العميل الجزء الخاص به من المفتاح (إلى جانب المعلمات الضرورية) وقائمة التواقيع المتاحة في الرسالة الأولى (Client Hello). يتم إنشاء المفاتيح اللازمة في هذه المرحلة من قبل العميل أثناء التنقل - حتى أن المستخدم لا يلاحظ ذلك. بعد ذلك ، يقوم العميل والخادم بتبادل هذه المعلومات لإنشاء سر مشترك - مفتاح جلسة يتم إنشاؤه (أو بشكل أكثر دقة ، يتم اشتقاقه) من الزوج التمهيدي الرئيسي الذي تم استلامه بعد استجابة الخادم للعميل برسالته (Server Hello).
في الجانب "Server Hello" ، يمكنك رؤية السجل المطابق لنقل الشهادة إلى العميل (Certificate *) ، مع التحقق من CertificateVerify * ، والذي يؤكد أن الطرف لديه بالفعل مفتاح خاص يتعلق بسجل المفتاح العام المقابل ، ثم إنشاء زوج مفاتيح (متماثل) للجلسة في حالة النجاح. بمعنى آخر ، قام الطرف الطالب (العميل) بالبيانات بالتحقق من صحة الطرف المستجيب (الخادم) بنجاح من خلال التبديل إلى استخدام سر مشترك.

تتم حماية عمليتي التشفير الرئيسيتين في هذا النقل - إنشاء توقيع والتحقق من التوقيع. عادةً ما يتم تنفيذ هذه العمليات في نهايات مختلفة من الاتصال ، حيث غالبًا ما يتحقق العملاء من صحة الخادم. التوقيع هو في الأساس تأكيد على ملكية المفتاح الخاص المطابق للمفتاح العمومي. أي أننا نتلقى بيانات من الموقع ، ونتأكد من عدم تغيير الرسالة أثناء النقل.

عند استخدام خوارزمية RSA ، كما سنعرض بعض الأرقام في وقت لاحق ، فإن عملية إنشاء توقيع هي الأغلى. نظرًا لأننا نوقع مع مفتاح 2048 أو 3072 بت ، فإن مثل هذه العملية تقوم بتحميل الخادم بشكل كبير - أقوى بكثير من العميل أثناء عملية التحقق (التوقيع) الخاصة به.

في ECDSA ، نعمل باستخدام مفاتيح قصيرة نسبيًا (في المثال المرجعي ، سننظر إلى ECDSA باستخدام منحنى NIST P-256 (أو secp 2566v1) ، ولكن هذه المفاتيح تشارك في عمليات أكثر تعقيدًا. ونتيجة لذلك ، يمكن استخدام ECC باستخدام RSA "مقلوب" مع وجهات نظر الأداء: يتم تحميل العميل أكثر صعوبة مع عملية التحقق من التوقيع ، في حين أن الخادم يعالج عملية إنشاء التوقيع بسهولة ، كما يتضح من القياسات التي نقدمها في القسم القياسي.

يساعد هذا التأثير في توسيع نطاق الإنترنت - نظرًا لأن العملاء الحديثين يتمتعون بنفس قوة الخوادم (إذا أخذنا في الاعتبار سرعة ساعة مركز المعالج) فقط ، فيمكنهم أن يقوموا بفعالية بعملية حسابية صعبة دون مشاكل. يمكن للخادم ، بدوره ، استخدام القدرة الحاسوبية المحررة لإنشاء المزيد من التواقيع ، ونتيجة لذلك ، إنشاء المزيد من الجلسات.

توقيع الشهادة في Let's Encrypt

سنزود القارئ بتعليمات بسيطة ومفهومة يمكنك من خلالها إنشاء خادم قادر على إنشاء جلسة TLS باستخدام زوج مفاتيح ECDSA يتم فيه توقيع Let's Encrypt وعليه يتم تضمينه في شهادة سلسلة الثقة كشهادة.
قررنا إظهار المسار الكامل من إنشاء المفاتيح ، وإنشاء طلب توقيع شهادة (CSR) لـ Let's Encrypt وإرساله للتوقيع باستخدام الأداة المساعدة certbot ، التي تُرجع السلاسل اللازمة وشهادة ECDSA نفسها.

تحتاج أولاً إلى إنشاء زوج رئيسي. لهذا سوف نستخدم مكتبة OpenSSL. يقول دليل مستخدم OpenSSL أن إنشاء مفاتيح للخوارزميات استنادًا إلى المنحنيات الإهليلجية يحدث باستخدام أمر خاص مخصص لعائلة الخوارزميات استنادًا إلى المنحنيات الإهليلجية.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem

للتحقق من عمل فريقنا بشكل صحيح ، نقوم بتنفيذ الأمر ec الذي يشير إلى المسار إلى الملف الذي تم إنشاؤه حديثًا والذي يحتوي على المفتاح الخاص.

 openssl ec -in privatekey.pem -noout -text

يجب أن يوضح لنا الناتج المنحنى المستخدم ، والذي تم به إنشاء المفتاح.

الخطوة التالية مهمة جدًا عند إنشاء CSR - حتى لا يتم ملء الاستبيان اللازم لتوقيع الشهادة في كل مرة ، نحتاج إلى ملف تهيئة. لحسن الحظ ، تم تنفيذ جميع الأعمال تقريبًا من قِبل Mozilla ، مما أدى إلى إنشاء " SSL Configuration Generator ". في ذلك ، يمكنك الاختيار من بين مجموعة متنوعة من الخيارات لأوضاع الخادم التي يمكنك من خلالها تأسيس اتصال TLS. تبدو تهيئة OpenSSL النظيفة ، لسبب ما مفقودة من مولد Mozilla ، كما يلي:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com

ملاحظة: ليس لديك ملف تكوين - إذا لم يكن هناك ، فسيُطلب منك ملء جميع الحقول في سطر الأوامر. مع ملف التكوين ، المسار الذي نحدده في الأمر التالي ، يتم تبسيط العملية.

التالي هو إنشاء طلب توقيع الشهادة (CSR) نفسه. لهذا ، لدينا فريق OpenSSL مناسب.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem

يمكننا أيضًا التحقق من صحة CSR المنشأة حديثًا.

 openssl req -in csr.pem -noout -text -verify

أخيرًا ، وصلنا إلى المرحلة النهائية - باستخدام عميل ACME ، certbot ، سننقل طلبنا للتوقيع على شهادة منظمة Let's Encrypt.

لن يساعدك Certbot في الحصول على شهادة فقط ، ولكن لديه أيضًا العديد من الخيارات الرائعة الأخرى. نضيف أنه إذا كنت جديدًا في التشفير باستخدام مفتاح عام ولم تفهم حقًا البنية الأساسية للمفتاح العام الموجودة حاليًا ، فمن الأفضل استخدام خيار --dry-run قبل محاولة الحصول على شهادة حقيقية لأي من نطاقاتك.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem

في هذه الحالة ، يتحقق عميل certbot من تطابق قائمة المجالات المطلوبة المطلوبة في سطر الأوامر مع القائمة في طلب توقيع الشهادة (CSR). داخل --dns-somednsprovider بعض الشيء ، حيث توجد عدة طرق لتأكيد Let Encrypt بأنك تمتلك جزءًا معينًا من حركة مرور الإنترنت. ولكن إذا كنت تستخدم نوعًا من مزود الخدمة السحابية ، مثل DigitalOcean و AWS و Azure و Hetzner ، أيا كان - فقد يكون لديك بالفعل طريقة أسهل لتوفير المعلومات التي تحتاجها لإصدار الشهادات ، لأن مزود الخدمة قد اعتنى بأداة التكامل.

بعد ذلك ، إذا كنت متأكدًا من أن المعلمات التي تم تمريرها إلى CSR باستخدام certbot إلى Let's Encrypt صحيحة ، --dry-run سوى إزالة --dry-run من الأمر والمتابعة.

إذا نجح العميل ، فسوف يعيدك إلى عدة شهادات: الشهادة الموقعة نفسها ، الشهادات المتوسطة والجذر ، بالإضافة إلى مزيج من الشهادات الأخيرة في شكل سلسلة من الشهادات ، كل ذلك بتنسيق .pem.

يحتوي OpenSSL على أمر نستخدمه للبحث داخل الشهادة:

 openssl x509 -in chainfilepath.pem -noout -text

يجب أن يكون من الواضح الآن أن Let's Encrypt وقّع الشهادة باستخدام خوارزمية تجزئة SHA256. بالإضافة إلى ذلك ، يخطط Let's Encrypt فقط لإضافة توقيعات الجذر والوسيط إلى ECDSA ، لذلك يبقى الآن أن يكون المحتوى بتوقيعات RSA الوسيطة. لكن هذا ليس مخيفًا ، لأنه على أي حال ستستخدم المفتاح العمومي ECDSA.

في نهاية هذا القسم ، نود إضافة بعض المعلومات حول مقارنة الأطوال الرئيسية للعديد من الخوارزميات. في أمان المعلومات ، من المعتاد القول أن مستوى الأمان هو 2 ^ x ، حيث x طول البتة (RSA استثناء ، لأنه ينمو أبطأ نوعًا ما من الأس). لتقريب كيفية مقارنة مفاتيح الخوارزميات المختلفة ، نشير إلى صفحة الويكي OpenSSL :

طول مفتاح متماثل	RSA طول المفتاح	الاهليلجيه منحنى طول المفتاح
80	1024	160
112	2048	224
128	3072	256
192	7680	384
256	15360	512

كما ترون ، فإن الاختلافات ملحوظة. على الرغم من أنه في الوقت الحالي ، يتيح لك Let's Encrypt تلقي شهادات موقعة فقط على مفاتيح منحني بيضاوي فقط - 256 (secp256v1) و 384 (secp384r1).

الصعوبات المعروفة وكذلك وكالة الأمن القومي

بواسطة: xkcd

ربما كانت المشكلة الرئيسية في استخدام التشفير القائم على منحنيات إهليلجية هي الحاجة إلى مولد أرقام عشوائي يتم تنفيذه بدقة شديدة ، وهو أمر ضروري لإنشاء مفاتيح لمستوى أمان معين.

ارتبطت فضيحة ضخمة بخوارزمية Dual_EC_DRBG - لقد استغرق الأمر سنوات عديدة لحلها. هناك شكوك حول قاعدة براءات الاختراع حول ECC - من المعروف أن العديد من براءات الاختراع تخص Certicom ، التي حصلت عليها Blackberry. هناك أيضًا العديد من حالات شهادات Blackberry ECC المعروفة. أخيرًا ، هناك بعض عدم الثقة في معايير NIST ، والتي يمكن أن تتأثر بـ NSA أو أي وكالة استخبارات أمريكية أخرى.

تعتبر الأخطاء في تنفيذ معايير التشفير موضوعًا متعامدًا تمامًا. في عام 2010 ، عانى جهاز PlayStation 3 من تسرب مفتاح Sony الخاص بسبب التنفيذ الخاطئ لخوارزمية ECDSA - لم تتمكن Sony من التعامل مع RNG وقدمت نفس الرقم العشوائي ، مما أتاح حل الوظيفة باستخدام إدخال سري. عانى OpenSSL في العام التالي ، إلا أنه سرعان ما أصلح ثغرة أمنية سمحت له بالحصول على مفتاح خاص باستخدام هجوم زمني - يمكن العثور على مزيد من التفاصيل في المنشور البحثي الأصلي .

في مؤتمر RSA في عام 2013 ، قدمت مجموعة من الباحثين ورقة بحثية بعنوان " فشل عشوائيًا! "مخصصة لضعف الطبقة Java SecureRandom. بعد ستة أشهر ، بدأت الأمور باستخدام محافظ Bitcoin التي تم إنشاؤها باستخدام مولد أرقام عشوائية زائف غير مشفر.

نظرًا لحقيقة اكتشاف العديد من نقاط الضعف الخطيرة في فترة زمنية قصيرة ، في نفس أغسطس 2013 ، أصدر IETF RFC 6979 ، الذي يصف الجيل الحتمية k عند إنشاء مفتاح. يمكننا أن نكتب أن المشكلة قد تم حلها بهذه الطريقة ، لكننا لن - في أي وقت ، قد يجد الباحثون أخطاء جديدة في التنفيذ بسبب الانحرافات غير الضرورية عن مواصفات البروتوكول.

وبعض الكلمات عن وكالة الأمن القومي. إذا لم تكن على دراية بتاريخ Dual_EC_DRBG - خذ بعض الوقت وقراءة المواد ذات الصلة ، فلن نأسف لأنك تعرفت على التفاصيل. أصبح إدوارد سنودن جزءًا من هذه القصة ، لأنه بسبب تسريباته في عام 2013 ، تم تأكيد كل الشكوك الموجودة. أدى ذلك إلى حقيقة أن العديد من أجهزة التشفير المرموقة فقدت الثقة في NIST ، حيث أن هذه المنظمة هي التي قامت بإنشاء ووصف العديد من المنحنيات الإهليلجية والخوارزميات التي تعمل في ECDSA.

منحنى 25519 من تأليف دانييل Burnshite ووظيفة Diffie-Hellman للتوزيع الرئيسي هو الإجابة على العديد من الأسئلة أعلاه. وكما كتبنا بالفعل ، هناك حركة ثابتة نحو EdDSA. في حالة منحنيات NIST ، لم يتم العثور على أي تأكيد لضعفها ، أما بالنسبة للتجربة مع الأرقام العشوائية ، فقد كانت مؤلمة للغاية وساهمت في الاستيعاب السريع.

في ختام هذا الجزء ، نود أن نقتبس من جون فون نيومان: "أي شخص لديه ضعف في الطرق الحسابية للحصول على أرقام عشوائية لا يخطئ في الخطية".

بعض المعايير

استخدمنا خادم NGINX 1.16.0 مع إصدار مكتبة OpenSSL 1.1.1d لإجراء اختبارات باستخدام شهادتين. كما ذُكر سابقًا ، في الوقت الحالي ، يتيح لك Let's Encrypt استخدام خوارزميات prem و 256 و secp384r1 فقط لإنشاء طلب توقيع شهادة ، بالإضافة إلى عدم تقديم شهادات الجذر والشهادات الوسيطة بتوقيع ECDSA ، وربما تتعامل مع هذه الميزة أثناء قراءة هذه الملاحظة.

نوع التوقيع	المصافحة في الثانية
ECDSA (prime256v1 / nistp256)	3358.6
RSA 2048	972.5

كما ترون ، على جوهر واحد من وحدة المعالجة المركزية Intel® Xeon® Silver 4114 @ 2.20 جيجاهرتز (صدر في الربع الثالث من 17) ، فإن الفرق الإجمالي بين أداء ECDSA و RSA المقبول عمومًا بطول رئيسي يبلغ 2048 بت هو 3.5 مرات.

دعونا نلقي نظرة على نتائج تشغيل الأمر openssl-speed لـ ECDSA و RSA على نفس المعالج.

نوع التوقيع	علامة	تحقق من	علامة / ثانية	تحقق / ثانية
RSA 2048 بت	717 μs	20.2 μs	1393.9	49458.2
256 بت ECDSA (nistp256)	25.7 μs	81.8 μs	38971.6	12227.1

هنا يمكننا العثور على تأكيد لأطروحة مكتوبة مسبقًا حول كيفية اختلاف العمليات الحسابية للتوقيع والتحقق منه بين ECC و RSA. حاليًا ، مع تشفير TLS 1.3 ، يوفر التشفير بناءً على منحنيات إهليلجية زيادة كبيرة في أداء الخادم مع مستوى حماية أعلى مقارنة بـ RSA. هذا هو السبب الرئيسي الذي يجعلنا في Qrator Labs نوصي ونشجع بشدة العملاء المستعدين لاستخدام شهادات ECDSA أيضًا. على وحدات المعالجة المركزية الحديثة ، فإن مكسب الأداء لصالح ECDSA هو 5x.

إذا كنت مهتمًا بكيفية معالجة معالج (المنزل أو الخادم) للحوسبة المشفرة ، فقم بتشغيل الأمر opensl speed. تتيح لك -eddsa و -eddsa و -eddsa تحديد خوارزميات الاهتمام -eddsa .

المستقبل (في التراكب)

ومن المفارقات أنه أثناء عملية كتابة هذه المادة ، أعلنت Google عن "تحقيق تفوق كمي" . هل هذا يعني أننا في خطر بالفعل وأن كل التقدم المحرز حتى اللحظة الحالية لم يعد قادراً على ضمان السرية؟

كلا.

كما كتب Bruce Schneier في مقالة "التشفير بعد Alien Landing" من أجل IEEE Security and Privacy Circular ، يمكن للكمبيوتر الكمومي حقًا توجيه ضربة خطيرة فقط للتشفير غير المتماثل باستخدام مفتاح عمومي. ستبقى الخوارزميات المتماثلة ثابتة.

ولكن للمتابعة ، سنعطي الكلمة للسيد شنير نفسه:

هناك سيناريو آخر في المستقبل لا يتطلب جهاز كمبيوتر كميا. في حين أن لدينا الآن العديد من النظريات الرياضية التي تقوم عليها النظرية الأحادية المستخدمة في التشفير ، فإن إثبات صحة هذه النظريات هو في الواقع أحد أكبر المشكلات المفتوحة في علوم الكمبيوتر. مثلما يستطيع مصور التشفير الذكي العثور على خدعة جديدة تسهل اختراق خوارزمية معينة ، يمكننا أن نتخيل الأجانب بنظرية رياضية كافية للقضاء على جميع خوارزميات التشفير. اليوم يبدو سخيفا. تشفير المفتاح العام هو نظرية الأعداد ويحتمل أن تكون عرضة للأجانب ذوي العقلية الحسابية. تشفير متماثل غير خطي ، وبسيط للغاية لإنشاء وتعقيد ، وكذلك مدى سهولة إطالة المفاتيح ، ما مستقبل لا يمكن تصوره. مثال على ذلك هو متغير AES مع كتلة 512 بت وحجم المفتاح ، وكذلك 128 طلقة. إذا كانت الرياضيات لا تختلف اختلافًا جوهريًا عن فهمنا الحالي ، فستكون هذه الخوارزمية آمنة حتى يتم تصنيع أجهزة الكمبيوتر من شيء آخر غير المادة وتحتل شيئًا آخر غير الفضاء.

ولكن إذا حدث ما لا يمكن تصوره ، فستترك لنا فقط مع تشفير يعتمد فقط على نظرية المعلومات: دفاتر الشفرات التي يمكن التخلص منها ومتغيراتها.

يصف Bruce Schneier تمامًا المنطقة التي توجد بها نقاط الضعف الرئيسية في التشفير الحديث ، بالإضافة إلى أخطاء التنفيذ. إذا كان هناك في مكان ما مجموعة من علماء الرياضيات الأثرياء ومحللي التشفير ومشفرات التشفير ، إلى جانب مهندسي الكمبيوتر الذين يعملون على إثبات أو دحض بعض المشكلات الرياضية المعقدة بشكل خاص (مثل P؟ = NP) ، الذين تمكنوا من تحقيق بعض التقدم في هذا النشاط في الوقت الحالي - موقفنا ضعيف. من خلال رفض نظريات المؤامرة ، يمكن للمرء أن يقول أن مثل هذا التقدم في مجالات علوم الكمبيوتر ، نظرية المعلومات ، ونظرية الحوسبة لا يمكن أن يكون مخفيًا. كان مثل هذا الحدث قد أدخل أسماء منشئيهم على صفحات التاريخ ، وعلى وجه الخصوص ، في الكتب المدرسية لتاريخ الإنترنت ، والتي لا تقدر بثمن لأي فرد أو مجموعة ذكية للغاية. لذلك قد يتم تجاهل سيناريو مشابه على أنه مستحيل.

ومن غير الواضح أيضًا ما إذا كانت هذه النجاحات في الحوسبة الكمية ستتحقق في السنوات الخمس المقبلة - وهناك بالفعل بدائل تشفير مناسبة للاستخدام في عالم ما بعد الكم: المشابك ، باستخدام isogenization الفائق للمنحنيات الإهليلجية ووظائف التجزئة ورموز تصحيح الأخطاء. الآن ، يقوم خبراء الأمن بإجراء تجارب معهم فقط ، ولكن لا شك في أن البشرية ، إذا لزم الأمر ، ستجد طريقة لنشر خوارزميات جديدة بسرعة على أي نطاق.

يبقى فقط أن نضيف أنه على مدى العقد المقبل ، يبدو أن التشفير على أساس المنحنيات الإهليلجية مناسب بشكل مثالي للأهداف والاحتياجات التي حددها معظم مستخدميها لأنفسهم ، مما يوفر الأمان والأداء العالي.

كيف يعمل تشفير المنحنى الإهليلجي في TLS 1.3