تتريس كطابعة

عند تشغيل تسلسل من الأشكال المحددة مسبقًا وإعادة ترتيبها وخفضها ، تستخدم خوارزمية طابعة Tetris آليات Tetris لإنشاء صور نقطية عشوائية.

وصف الخوارزمية

تقوم الخوارزمية بتحويل وحدات البكسل في الصورة المصدر إلى مربعات سطر حقل Tetris سطراً ، مع الانتقال من الأسفل إلى الأعلى. لإنشاء مربع واحد ، تقوم الخوارزمية بتجميع بنية تتكون من منطقة مستطيلة تدعمها بالكامل مربع واحد تحتها. بعد اكتمال تجميع المنطقة المستطيلة ، يتم مسح خطوطها ، تاركة مربعًا تحتها. فيما يلي ثلاثة أمثلة لهذا السلوك.




كما هو موضح أدناه ، يمكن للخوارزمية أيضًا إنشاء عدة مربعات ذات بنية واحدة.


في عملية بناء صف ، يجب أن تستند جميع المربعات التي تم إنشاؤها بهذه الطريقة إلى شيء ما. في الصور الموضحة أعلاه ، توجد المربعات التي تم إنشاؤها على أرض الملعب. ومع ذلك ، إذا كان الخط التعسفي يحتوي على ثقوب ، فلن يكون قادرًا على توفير الدعم اللازم لبناء خط فوقه. الخوارزمية تحل هذه المشكلة عن طريق إنشاء منصة مسطحة على رأس السلسلة مع الثقوب. في الرسوم المتحركة أدناه ، تتكون منصة مبنية على أعلى الخط من مربع أحمر واحد. النظام الأساسي عبارة عن هيكل مؤقت ، وإدراجه في الشكل الأخير يزيله.


صف 5 مربعات حمراء موضحة أدناه أعلى صف 3 مربعات حمراء. ويتحقق ذلك من خلال بناء منصة مسطحة في أعلى الخط السفلي. توفر المنصة الدعم اللازم لإنشاء 5 مربعات حمراء. في النهاية ، يتم حذف النظام الأساسي عن طريق إدخال الشكل الأخير ، ويقع الخط الجديد في مكانه. لاحظ أنه إذا كانت الخوارزمية تحتاج إلى إنشاء خطوط بالترتيب العكسي (سطر من 3 مربعات حمراء فوق خط من 5 مربعات حمراء) ، فلن تكون هناك حاجة إلى النظام الأساسي.

أنماط مربع واحد

للإشارة ، سأقدم أسماء 7 tetramino (قطع لعبة).


تم تصميم إصدار خوارزمية طابعة Tetris المقدمة في المقالة خصيصًا لتقديم العفاريت من ألعاب الفيديو القديمة. هذه الألعاب معبأة الرسومات في 8 × 8 البلاط ، و 2 بايت تم تخصيصها لكل بكسل. لذلك ، تحتوي العفاريت عادة على 3 ألوان فقط بالإضافة إلى مساحات شفافة وغالبًا ما يكون حجمها 16 × 16 أو 16 × 32 بكسل.

تظهر الرسوم المتحركة أدناه جميع الأنماط المستخدمة لإنشاء مربعات فردية. يستخدم كل نمط tetramino قابلة للتبديل J و T و L ، مما يخلق مربعًا واحدًا في الأسفل. تقوم الخوارزمية بتخصيص tetramino لأحد الألوان الثلاثة الموجودة في العفريت. يتم تعيين بقية tetramino الألوان التعسفي. طوال اللعب ، تظل جميع الألوان ثابتة.


بسبب شكل tetramino الثلاثة ، من المستحيل إنشاء مربع من كل الألوان الثلاثة في العمودين الأولين والأخيرين. لذلك ، يكون الحد الأدنى لعرض حقل اللعب لعرض شبح بعرض 16 بكسل هو 2 + 16 + 2 = 20 مربعات. ومع ذلك ، اتضح أن 20 هو القليل جدا.

كما هو موضح أدناه ، لا يمكن أن تتألف المنطقة الموجودة أعلى المربع السفلي من سطر واحد فقط ، لأن الأشكال الوحيدة التي يمكن وضعها فيه (tetramino I) لا تدعمها.


باستخدام سطرين ، فإن الطريقة الوحيدة لتمديد الملعب بالكامل بحيث يكون لديه دعم هي استخدام tetramino S و Z. ولكن في هذه الحالة ، ستظل الثقوب في السطر العلوي.


الحد الأدنى لعدد الخطوط المطلوبة أعلى المربع السفلي هو 3 ، وكما هو مبين عدة مرات أعلاه ، توجد مثل هذه الأنماط. 20 مربعات هي الحد الأدنى للعرض المطلوب لوضع العفاريت بعرض 16 بكسل. لكن 20 × 3 + 1 = 61 ، وهذا الرقم غير قابل للقسمة على 4 ، مما يعني أنه لا يمكن بناؤه من tetramino. ومع ذلك ، فإن العرض 21 يعطينا 21 × 3 + 1 = 64 ، ويمكن بناؤه من 16 tetramino. في الواقع ، يسمح هذا العرض للخوارزمية بعرض العفاريت بعرض يصل إلى 17 بكسل.

حجم ملعب Tetris الأصلي بحجم 10 × 20 مربع (نسبة 1: 2). في هذا الإصدار من الخوارزمية ، يتم الحفاظ على هذه النسبة - تبلغ مساحة الملعب 21 × 42 مربعًا.

نظرًا لأن tetramino J و T و L قابلة للتبديل عند إنشاء مربع واحد ، وتشارك 3 مربعات من tetramino في إنشاء خط فوقه ، هناك 21 - 3 = 18 نقش لإنشاء مربع واحد. ومع ذلك ، نظرًا للتناظر المرآة ، لا يوجد في الواقع سوى 9. هناك ثلاثة خطوط تعمل لمعظم هذه 9. ومع ذلك ، أظهرت دراسة كمبيوتر شاملة أن هناك حاجة إلى أكثر من اثنين من الأنماط. الخيار التالي الممكن هو 7 خطوط ، لأن 21 × 7 + 1 = 148 ، والذي يتطلب 37 tetraminos. كما هو موضح في الصور أدناه ، توجد هذه الأنماط.

أنماط مربع متعددة

تقتصر أنماط إنشاء مربعات متعددة على نفس الألوان الثلاثة التي تم إنشاؤها بواسطة أنماط مربع واحد. يتم إنشاء المربعات الناتجة من tetramino J و T و L ، ويشغل كل منها 3 مربعات في خط أعلى خط الإنشاء. الحد الأقصى لعدد المربعات التي يمكن إنشاؤها بنمط واحد هو 21/3 = 7. ومع ذلك ، بالنسبة للعفاريت التي يبلغ عرضها 16 بكسل ، يتعذر على tetramino الموجود في أقصى اليمين إنشاء مربع. حتى في حالة العفاريت التي يبلغ عرضها 17 بكسل ، يمكنها إنشاء مربع بلون واحد فقط. لذلك ، نادراً ما يتم استخدام نمط الإنشاء من 7 مربعات.


يمكن تحديد عدد أنماط إنشاء عدد عشوائي من المربعات باستخدام مجموعات التعدادات. النظر في نمط أدناه ، يمثل صف أعلى صف من ثلاثة مربعات. كل كتلة من ثلاثة مربعات بيضاء مجاورة تعين جزءًا من tetramino ؛ لا تظهر المربعات التي تم إنشاؤها.


ثلاثة tetramino خلق 4 فراغات. هناك 21 - 3 × 3 = 12 المربعات المظلمة التي يمكن إدراجها بشكل تعسفي في هذه الفراغات لتشكيل نمط معين. يمكن حساب عدد طرق توزيع هذه المربعات الداكنة عن طريق وضعها على خط تعامل فيه المربعات البيضاء المفردة على شكل فواصل.


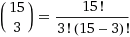
لذلك ، تم تخفيض المهمة لحساب قيمة معامل كثير الحدود. بالنظر إلى هذه المربعات البيضاء ، يمكنك أن تفهم أن هذه هي مسألة عدد طرق اختيار 3 من 15. = 455.

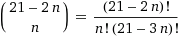
في الحالة العامة ، لأنها تساوي . لكن بسبب التناظر المرئي ، فهي في الحقيقة نصف. إذا كانت الكمية غريبة ، ثم قسمة على اثنين ، فنحن ننتقل إلى أقرب عدد صحيح لتضمين النمط المتماثل المثالي الذي يجب أن يوجد في هذه المجموعة ، كما هو موضح أدناه على سبيل المثال بالنسبة للحالة مع 455.


بتطبيق هذه الصيغة على 7 tetramino ، نؤكد ما هو واضح: هناك نمط واحد فقط لإنشاء 7 مربعات.

يمكن إنشاء نمط إنشاء 6 مربعات بطريقتين: خطان مملوءان (2 × 21 + 6 = 48) وستة خطوط مملوءة (6 × 21 + 6 = 132) ، والتي تتطلب 12 و 33 tetramino. توضح الصيغة أعلاه أن هناك 84 نموذجًا لإنشاء 6 مربعات ، ولكن يمكن بناء 35 منها فقط من خطين كاملين. 49 أنماط تتطلب 6 خطوط. الأرقام غريبة بسبب الأنماط المتماثلة الموضحة أدناه.



تجدر الإشارة أيضًا إلى أن هناك سطرين ممكنان هنا ، لأنه على عكس نمط إنشاء مربع واحد يتطلب tetramino S و Z ، يتم استخدام 6 أشكال في هذه الأنماط.

يوضح الجدول أدناه عدد المربعات التي تم إنشاؤها بواسطة كل نوع من أنواع النماذج ، وعدد الأسطر الكاملة ، وعدد tetramino المستخدم ، وعدد الأنماط.


أمثلة على الأنماط.

منصة

قبل إنشاء خط ، تقوم الخوارزمية بفحص الخط الموجود تحته. إذا لم يتمكن الصف السفلي من توفير الدعم لجميع المربعات الموجودة فوقه ، فستكون هناك حاجة إلى منصة مؤقتة. عند إزالة المنصة ، ينهار خط جديد ، وبسبب كيفية تطبيق الجاذبية في Tetris الأصلية ، تظل بعض المربعات معلقة في الهواء.

يوضح الرسم التوضيحي أدناه 10 أنماط للمنصات. يبدأ إنشاء المنصة بخفض tetramino T أعلى أحد مربعات السطر الأخير الذي تم إنشاؤه. تعتمد tetraminos المتبقية على هذا T. الأول ، إذا كان السطر الذي تم إنشاؤه سابقًا يحتوي على مربع واحد على الأقل ، مثل المربع الأحمر في الصورة أدناه ، فيمكننا إنشاء منصة مسطحة فوقه لإنشاء السطر التالي.


في منتصف بناء المنصة ، يتم إكمال الخط السفلي وحذفه ، تاركًا ثلاثة خطوط فوقه. لا يتم إدراج tetramino J أو L الأخير ، والذي سيؤدي إلى حذف هذه السطور ، حتى يتم إنشاء أنماط الإنشاء السطر العفريت التالي أعلى النظام الأساسي. يمنع هذا الشكل الأخير إنشاء مربعات في السطرين الأول والأخير. ولكن ، كما ذكر أعلاه ، نظرًا لهندسة tetramino J و T و L المستخدمة في هذه العملية ، تقتصر أنماط إنشاء المربعات على 17 عمودًا داخليًا.

بالإضافة إلى ذلك ، من بين 19 طريقة ممكنة لإنشاء منصات على Tetramino T ، هناك 10 طرق فقط معروضة أعلاه.

المصفوفات معبأة

كما ذكر أعلاه ، تتضمن مجموعة فرعية من أنماط إنشاء المربعات الستة مسح سطرين فقط. جميع الأنماط الأخرى تتطلب 6 خطوط. لفهم سبب هذا ، فكر في النموذج أدناه.


هذه tetramino قابلة للتبديل مع tetramino J و L ، ويضيف كل منها 3 مربعات متجاورة إلى الصف المشترك. يتم تمثيل الصفوف المراد إكمالها بالمصفوفة الموضحة أدناه.


الآن كل شيء هو تعبئة مساحة فارغة مع tetramino. بدءًا من اليسار ، فإن الخيار الوحيد هو استخدام تسلسل tetramino I.


الطريقة الوحيدة لملء المساحة المتبقية هي استخدام J و O أو I و L. ويرد كلا الخيارين أدناه.



لسوء الحظ ، لا يتم دعم tetramino O و L في المصفوفات الموضحة أعلاه. هذا النمط 6 مربعات يتطلب مصفوفة أكبر.

تنشأ مشكلة مماثلة في نمطين لإنشاء مربع واحد. النظر في المصفوفة أدناه:


الطريقة الوحيدة لملء الخط السفلي على اليمين هي سلسلة التسلسل Z.


وبالمثل ، فإن الطريقة الوحيدة للحصول على 3 مربعات فارغة في أسفل اليسار هي tetramino S.

في الخط الأوسط يوجد مربع فارغ بين S و Z ، والطريقة الوحيدة لملئه هي استخدام tetramino J أو T أو L ، كما هو موضح في الأشكال أدناه.



يؤدي إدراج أي من هذه الأشكال إلى تقسيم المساحة الفارغة. تحتوي المساحة الفارغة على اليسار على 5 و 6 و 7 فراغات ، على التوالي. بما أنه لا يمكن تقسيم أي من هذه القيم على 4 ، فمن المستحيل المتابعة. مطلوب مصفوفة أكبر لهذا النمط مربع واحد.

الأمر نفسه ينطبق على نمط آخر لإنشاء مربع واحد ، كما هو موضح في المصفوفة أدناه.


بعد استخدام tetramino S و Z لملء معظم الخط السفلي ، هناك مسافة فارغة بينهما في الخط الأوسط.


كما هو موضح في الصور أدناه ، يقسم إدراج الفتحة المساحة الفارغة ، وتحتوي المنطقة الفارغة على اليسار على 9 أو 10 أو 11 مربعًا على التوالي ؛ أيا من الأرقام قابلة للقسمة على 4.



لكن مصفوفات التعبئة ليست هي الطريقة الوحيدة لإنشاء نمط مربعات. على سبيل المثال ، ألق نظرة على منشئ المربعات الأربعة أدناه.


فيما يلي محاولة لتقديم النموذج كمجموعة من tetraminos المعبأة.


تم تخطي علامة L الأخيرة ، لأن المساحة المخصصة لها لا تتشكل إلا بعد الانتهاء من الصف الثالث وإزالته.

ولكن بعد إجراء بحث شامل ، تم اكتشاف أن هذه التقنية لا توفر أنماط مربعة واحدة المذكورة أعلاه مع القدرة على العمل مع 3 خطوط فقط. بالإضافة إلى ذلك ، لا يسمح لها بتنفيذ أي أنماط جديدة من 6 مربعات في سطرين. ليست هناك حاجة للبحث عن الأنماط المتبقية خارج المصفوفات المعبأة ، لأنها تستخدم بالفعل أصغر كمية ممكنة من tetramino. وبتقييد أنفسنا على المصفوفات المحزومة ، سنجد كل النماذج الضرورية أسرع بكثير.

البحث عن الأنماط

لتبسيط إخراج البيانات ، تقتصر خوارزمية طابعة Tetris على إنشاء tetramino في أعلى مركز الملعب ، وتحريكه ، والتحرك أفقيًا وخفضه. لم يكن مضطرا ابدا لتحريك الرقم أفقيا بعد اجتيازه مسافة. يقلل هذا التقييد من مساحة البحث إلى حد كبير ، لأنه لا يسمح بتكوين فجوات تحت الأشكال المضافة إلى المصفوفة. كمثال ، دعنا ننظر إلى مصفوفة المربعات الثلاثة التالية.


إذا ألقينا بـ J في وسط المصفوفة ، كما هو موضح أعلاه ، فسنحصل على فجوة مكونة من مربعين فارغين ، لا يمكن ملؤها بالأرقام اللاحقة. لذلك ، لن يتبع البحث هذا المسار.


نظرًا لأن الفجوات المغطاة غير مسموح بها ، يمكن اعتبار كل عمود في المصفوفة كومة من المربعات المملوءة ويصف ارتفاع هذه المداخن وصفًا كاملاً لمحتويات المصفوفة بأكملها. بغض النظر عن عدد الصفوف ، ستكون صفيف عدد صحيح أحادي البعد يحتوي على 21 عنصرًا كافيًا لوصف مصفوفة ثنائية الأبعاد.

عندما يقع الشكل في المصفوفة ، تزداد ارتفاعات مكدسات الأعمدة المقابلة. لتسريع هذه العملية ، يتم تحليل جميع tetramines مقدما. هناك 19 دورة tetramino ، ويعتبر البحث أن كل واحد منهم يمثل شخصية فريدة من نوعها.


يشغل Tetramino J في الزاوية اليسرى العليا من الصورة 3 أعمدة. عند التخفيض على المصفوفة ، تزداد ارتفاعات 3 مداخن متجاورة بنسبة 1 و 1 و 2 مربعات ، على التوالي. ولكن قبل أن يمكن خفض الرقم ، يجب أن يتوافق المظهر الجانبي السفلي للشكل مع المظهر الجانبي العلوي للمكدسات المعنية. إذا كانت هذه اللعبة J ملقاة على أرض الملعب ، فستكون هناك فجوات في المربعات الفارغة 1 و 1 و 0 تحت كل عمود من هذه الأعمدة. نظرًا لأن عمليات التطهير محظورة ، فإن الارتفاع النسبي لـ 3 رصات يجب أن يتطابق تمامًا مع النمط.

وكانت النتيجة الأخرى لعدم وجود فجوات أنه عندما تقع الأرقام في المصفوفة ، تمتلئ الصفوف من الأسفل إلى الأعلى. لا يمكن ملء صف في منتصف المصفوفة قبل أو في نفس الوقت عدم إكمال جميع الصفوف الموجودة أسفلها. في عملية ملء المصفوفة ، يتحرك الحد السفلي فعليًا للأعلى. لذلك ، يمكن أن يوفر مكدس أعمدة المصفوفة الدعم فقط إذا كان ارتفاعه ناقصًا عدد الصفوف المكتملة أكبر من 0. عند إضافة شكل إلى المصفوفة ، يجب أن يوفر أحد الأعمدة المطابقة على الأقل الدعم.

يقوم البحث بتخزين صفيف أحادي البعد يحتوي على عدد المربعات المملوءة في كل صف. يحتوي J أعلاه في الأسطر المقابلة 3 و 1 a مربع. عند إدراجه في المصفوفة ، تتم إضافة هذه القيم إلى العناصر المقابلة للصفيف. عدد الأسطر المكتملة هو عدد العناصر بقيمة 21.

كما هو مذكور في القسم السابق ، إذا كان الرقم المضاف يقسم المصفوفة ، فيجب تقسيم أحجام المناطق الناتجة إلى 4. على سبيل المثال ، في الصورة أدناه ، تؤدي إضافة I إلى إنشاء منطقتين ، يحتوي كل منهما على 46 مربعًا فارغًا. بما أن 46 غير قابلة للقسمة على 4 ، لم يعد هناك أي طريقة لملء ما تبقى من المصفوفة.


يظهر الفصل عندما يكون ارتفاع المكدس مساوياً لارتفاع المصفوفة. بعد إدراج الشكل عن طريق زيادة ارتفاعات المكدسات ذات الصلة ، يمكن تحديد أبعاد كل المساحات المقسمة من المساحة الفارغة عن طريق مسح صفيف المرتفعات وإضافة المساحة المتبقية في كل رصة. يتم فحص هذا الرقم وإعادة ضبطه عند اكتشاف انقسام.

يستخدم البحث المستخدم لإنشاء كل الأنماط بنية تدريجية عشوائية ، وهي خوارزمية تراجعية تقوم بفحص جميع المجموعات بشكل منتظم بترتيب عشوائي. البناء الإضافي للحل عن طريق إدخال الأشكال عشوائياً يجعله ينمو مثل البلورة. يوفر Randomness عدم انتظام يحتوي على الوجوه المكسورة التي تعمل كأساس للأشكال المضافة اللاحقة. يتم حزم معظم المصفوفة بشكل سريع جدًا ، وعندما تصبح المساحة الفارغة شحيحة ، يبدأ التراجع.

قبل إجراء البحث ، يتم تنفيذ التباديل العشوائي لـ 371 طريقة لإضافة رقم إلى المصفوفة. يظهر الرمز الزائف لوظيفة البحث أدناه.

private Result search(Matrix matrix, int remaining) { if (remaining == 0) { return SOLUTION } attempts := attempts + 1 if (attempts >= MAX_ATTEMPTS) { return TIMEOUT } if (     S  Z) {        S  Z if (  ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION }       if (result == TIMEOUT) { return TIMEOUT } } }          for(   ,    ) {      if (   ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION }       if (result == TIMEOUT) { return TIMEOUT } } } return NO_SOLUTION } 

المصفوفة الأصلية التي تم تمريرها إلى وظيفة البحث فارغة ، باستثناء الصف السفلي الذي يحتوي على كتل من 3 مربعات متجاورة. يتم إرسالها مع عدد الأرقام المتبقية التي تحتاج إلى إضافتها. إذا كانت القيمة remaining هي 0 ، فإن المصفوفة تحتوي على الحل وتُرجع الدالة. تزيد كل مكالمة متكررة من العدد العالمي لمحاولات attempts . إذا تجاوز MAX_ATTEMPTS ، والذي له قيمة 1000 ، MAX_ATTEMPTS البحث مرة أخرى.

أما if الثالثة if حاولت إضافة tetramino S أو Z إلى أسفل المصفوفة إذا سمحت المساحة بذلك. معنى هذا هو تجنب مواقف مثل تلك الموضحة أدناه ، عندما تقضي الخوارزمية وقتًا في ملء جزء من المصفوفة ، وعدم القدرة على ملء الباقي بسبب نقص الدعم.


بفضل if فإنها سرعان ما تشكل منصة يمكن البناء عليها:


لمحاولة إضافة شكل إلى المصفوفة ، يجب إجراء عمليات التحقق أعلاه. تقوم الخوارزمية بالتحقق مما إذا كان الرقم سيحصل على الدعم ، بالنظر إلى الخطوط المكتملة. كما يتحقق لمعرفة ما إذا كان يقسم على 4 حجم كل مساحة فارغة الفردية التي تم إنشاؤها بواسطة إدراج الشكل.

تحويل الصور

خوارزمية طابعة Tetris يحول كل سطر من الصورة النقطية إلى سلسلة من التمريرات. عند الانتقال من اليسار إلى اليمين ، يُدخل كل مقطع بطريقة "جشع" tetramino J و T و L إلى حيث يتم وضعهم. على سبيل المثال ، تعرض الصورة أدناه صفًا 16 بكسل من الصورة النقطية.


الصورة أدناه توضح 5 تصاريح اللازمة لتغطية هذه 16 بكسل.






يتم تحديد تسلسل الأشكال التي تحاول الخوارزمية إدراجها بواسطة ألوان وحدات البكسل. بحيث لا تتداخل الأشكال ، يتم استخدام مجموعة أحادية البعد من القيم المنطقية. لإدراج شكل ، يجب أن تكون 3 عناصر صفرية موجودة في الصفيف. عند الإدراج الناجح للشكل 3 ، تأخذ عناصر الصفيف المقابلة القيمة 1.

لتتبع البيكسلات المكتملة بين تمريرات متعددة ، يتم استخدام مجموعة ثانية أحادية البعد لقيم Boolean. عندما يكون كل عنصر 1 ، يكون الخط كاملاً.

في نهاية كل تمريرة ، يبحث محول الصور في الجدول عن كل الأنماط لإنشاء مربع أو أكثر. بالنسبة للإخراج ، فإنه يمر بالنمط المقابل مع إدراج tetramino J و T و L في الأسفل ، على سبيل المثال ، يتم عرض أول مرور موضح أعلاه كنموذج التالي لإنشاء 5 مربعات:

البحث في الوقت الحقيقي

إن محول الصور الموضح في القسم السابق سريع للغاية لأنه يستخدم جدولًا ثابتًا يحتوي على جميع الأنماط لإنشاء المربعات ولا يبحث عنها في الوقت الفعلي. ومع ذلك ، يمكن أن يستخدم البحث في الوقت الفعلي أنماطًا غير موجودة في الجدول ، وبالتالي ، يقلل بشكل كبير مقدار tetramino اللازم لإنشاء الصورة. يستخدم المربعات التي تم إنشاؤها في مقاطع سابقة ، واستخدامها كدعم إضافي. على سبيل المثال ، كما ذكر أعلاه ، يتطلب النمط التالي لإنشاء مربع واحد 7 خطوط كاملة.


ولكن مربع أحمر واحد تم إنشاؤه في المقطع السابق في الركن الأيسر السفلي من الصورة أدناه يوفر دعمًا إضافيًا ، مما يقلل من عدد الخطوط المملوءة إلى 3.


بالإضافة إلى ذلك ، يمكن أن يشمل البحث في الوقت الفعلي 3 بكسلات متجاورة من نفس اللون عن طريق قلب tetramino J أو T أو L.


في الواقع ، يمكن أن تجمع tetramino المقلوبة والمقلوبة ، وتغطي عددًا كبيرًا من البكسلات في مسار واحد. على سبيل المثال ، يمكن تخفيض الممرات الخمسة المذكورة أعلاه اللازمة لتغطية 16 بكسل إلى التمرير الفردي الموضح أدناه.


للحصول على هذا النمط ، يبدأ محول الصور بالتعبئة بفارغ الصبر tetramino المقلوبة J و T و L.


ثم يحاول بفارغ الصبر إضافة الإصدارات غير المنقولة ، وفي هذه الحالة يتمكن من إضافة J.


من حيث المبدأ ، يمكن أيضًا استخدام جدول بحث محسوب مسبقًا في هذه العملية ، ولكن الحجم الهائل لمثل هذا الجدول يجعله غير قابل للتطبيق في الممارسة العملية.

في هذا المثال ، تتم إضافة 8 مربعات في صف أعلى الصف المراد إنشاؤه إلى الصف السفلي من المصفوفة الفارغة. بالنسبة إلى المربعات n في ملعب مساحته 21 قدمًا مربعًا ، يكون ارتفاع المصفوفة h أصغر عدد صحيح موجب مثل 21h - n قابل للقسمة على 4. في هذه الحالة ، يلزم مصفوفة الارتفاع 4.


يعمل البحث في الوقت الفعلي بالطريقة نفسها التي تعمل بها خوارزمية البحث الموضحة أعلاه ، ولكنه يتضمن تحسينات طفيفة. كما كان من قبل ، يوفر مكدس عمود المصفوفة الدعم فقط إذا كان ارتفاع العمود ناقصًا عدد الصفوف المكتملة أكبر من الصفر. عندما يكون الفرق صفراً ، يجب ألا يوفر مكدس العمود الدعم. ومع ذلك ، في هذا الإصدار ، إذا كان يساوي الصفر ، فإنه يتحقق المربعات في السطر الذي تم إنشاؤه بواسطة التمريرات السابقة. أي أن المربعات في الصف أسفل الصف السفلي من المصفوفة توفر الدعم للأعمدة الفارغة.

بالإضافة إلى ذلك ، نظرًا لأن البحث يتم في الوقت الفعلي ، فسيكون من غير العملي جعله شاملًا. إذا لم يجد حلاً بعد عدد معين من المحاولات ، فسيضيف 4 صفوف أخرى في أعلى المصفوفة ، ثم يحاول مرة أخرى. بعد ذلك ، إذا كان لا يزال غير قادر على إيجاد حل بعد عدد معين من المحاولات ، فإنه في المقطع الحالي يعود إلى الطريقة مع جداول البحث المحسوبة مسبقًا وتحويل الصور الموضحة في القسم السابق من المقالة.

طباعة

للطباعة ، يجب اتباع الإرشادات التي يعرضها محول الصور في ملعب Tetris. تقوم الطابعة بإنشاء tetramino معيّن في أعلى مركز الملعب في اتجاه قياسي. ثم تقوم الطابعة بتدويرها وتحريكها أفقياً وتخفيضها. تظهر هذه العملية في الفيديو:

شفرة المصدر

الكود المصدري لمشروع Java 7 متوفر هنا .

توجد خوارزميات البحث للجداول المعدة مسبقًا والوقت الفعلي في الحزم search.precomputed و search.realtime . يستخدمون بعض الفئات الشائعة الموجودة في حزمة search . يتم تخزين نتائج البحث المحسوب مسبقًا في حزمة patterns كتسلسل من الملفات النصية. تخزن الملفات النصية المصفوفات المحزومة كأحرف ASCII ، بدءًا من A على سبيل المثال ، تبدو المصفوفات الثلاثة الأولى في emitters1.txt (مجموعة الأنماط لإنشاء مربع واحد) كما يلي:


كما ذُكر مرارًا في المقالة ، 3 يمكن استبدال الرموز A الموجودة في المصفوفات أعلاه بـ tetramino J أو T أو L. تمثل الرموز B و C و D وما إلى ذلك تسلسل tetramino الذي تحتاج إلى إنشائه.

تحتوي فئة imageconverter.ImageConverter على الطريقة main ، والتي تتلقى وسيطة سطر أوامر واحدة: اسم ملف الصورة sprite. لا يمكن أن تكون الصورة أكبر من 17 × 32 بكسل ولا يمكن أن تحتوي على أكثر من 3 ألوان معتمة. يجب أن تكون جميع وحدات البكسل الأخرى شفافة.

ومن المثير للاهتمام ، في ألعاب الفيديو القديمة ، غالبًا ما يستخدم المطورون الخلفية للحصول على ألوان إضافية. على سبيل المثال ، تلاميذ وفم Bubble من Bubble bobble ، تلاميذ Donkey Kong من Donkey Kong وحواجب مع ملكة جمال Pakman من السيدة. باك مان هو في الواقع شفافة. يتم الحصول على الأسود من خلفية صلبة.


يمكن استخدام خلفية ملعب Tetris بطريقة مماثلة.

ImageConverter إخراج ImageConverter :


القيم الثلاثية السداسية في السطر الأول هي 3 ألوان غير شفافة مستخرجة من ملف صورة العفريت. تتوافق مع ألوان tetramino J و T و L. لا تؤثر ألوان tetramino الأخرى على الصورة. الكتل المتبقية عبارة عن أنماط مغلفة يتم تنفيذها في ساحة اللعب (للأحرف بعد Z وما يصل إلى a راجع جدول أحرف ASCII ). الكتل الصفراء المميزة تشكل المنصة. الكتلة الأولى تضيف المنصة ، والثانية تزيلها.

يستقبل فئة printer.Printer ملفًا نصيًا بهذا التنسيق ويقوم بإنشاء ملف صورة عن طريق تشغيل Tetris.

تحدد خوارزمية الطابعة المستخدمة لإنشاء فيديو يشبه إصدار NES من Tetris كل نوع من أنواع tetramino في كل كتلة من الملفات النصية. ثم ينتقل بالترتيب المعاكس من نقطة البداية والاتجاه الأولي إلى زاوية الدوران وإحداثيات خفض الشكل الموضح في الملف. ملاحظة: نظرًا للسرعة العالية للغاية في انخفاض الأرقام ، من المستحيل تجاوز المستوى 30 في إصدار NES الحقيقي من Tetris. من المفترض أن الطابعة تنقل جميع أوامرها إلى الملعب بسرعة كافية. للتعويض عن هذا.

لتجديد ملفات الأنماط ، استخدم search.precomputed.PatternSearcher . يمكن تخصيصها عن طريق تغيير الثوابت في بداية ملف التعليمات البرمجية المصدر.

 public static final int MATRIX_WIDTH = 21; public static final int MATRIX_HEIGHT = 4; public static final int EMITTED_SQUARES = 4; public static final int RANDOM_SETS = 100000; public static final int MAX_ATTEMPTS = 1000; 

RANDOM_SETS هو عدد التباديل العشوائي من 371 طريقة لإضافة شكل إلى المصفوفة. عند 100000 إلى 100000 ، يستغرق تهيئة التباديل عند بدء التشغيل عدة ثوانٍ. بالإضافة إلى ذلك ، يتطلب تخزينها أكثر من غيغا بايت من الذاكرة.

يتحكم MAX_ATTEMPTS في وقت تنفيذ البحث. تسمح القيمة الصغيرة نسبيًا البالغة 1000 للبحث بتجاهل البدايات العشوائية التي تفشل في إظهار نفسها جيدًا بسرعة. ومع ذلك ، من أجل إثبات أنه بالنسبة لحجم مصفوفة معين وعدد المربعات التي تم إنشاؤها ، لا يوجد حل ، فمن الضروري استكشاف مساحة البحث بالكامل بالكامل. للقيام بذلك ، يمكنك تعيين MAX_ATTEMPTS إلى Integer.MAX_VALUE .

تم العثور على ثوابت مماثلة في search.realtime.RealtimeSearcher ، والذي يستخدمه محول الصور. كما ذكر أعلاه ، تتطلب قيمة RANDOM_SETS كبيرة زيادة في الحد الأقصى للذاكرة ويؤدي إلى بداية أطول. يتحكم MAX_RETRIES في عدد المحاولات ، وبعد ذلك يستسلم البحث في الوقت الفعلي ويعود إلى البحث مع جدول محسوب مسبقًا.

ضع في اعتبارك أن خوارزميات البحث تستخدم 100٪ من وحدة المعالجة المركزية ، مما يخلق العديد من مؤشرات الترابط المتوازية متساوية في الحجم مع عدد المعالجات المتوفرة.