مرحبا يا هبر! أقدم إليكم ترجمة المقال
"شرح حدسي لاختبار الفرضيات والقيم P" لجوس كورستانجي.
قبل بضع سنوات ، قمت بأول وظيفة إحصائية لحسابهم الخاص لشركة لتوصيل الفواكه والخضروات. أربع وعشرون ساعة في اليوم ، مرت المنتجات الواردة من المزارعين ، قبل إرسالها إلى محلات السوبر ماركت ، من خلال قسم مراقبة الجودة. تم اختيار المنتجات بشكل عشوائي من قبل موظفي هذا القسم.
في التقرير السنوي ، لاحظوا أن الجودة هذا العام أقل من الجودة في الماضي: كان الفرق حوالي نصف نقطة بمقياس من 1 إلى 10.
ثم دعوني. اضطررت للإجابة على السؤال:
هل هذه النقاط 0.5 فرق كبير؟إذا كنت لا تعرف الإحصائيات ، فقد يبدو هذا السؤال غريبًا عليك. ولكن لا تقلق: الغرض من هذه المقالة هو إظهار كيف يمكنك الإجابة على هذا السؤال باستخدام اختبار الفرضيات ، والذي يُسمى أيضًا الاستدلال الإحصائي.
لعبة الأرقام: مساهمة تفاحة واحدة
تخيل أنك تفحص تفاحة من أجل الخير أو السيئة ، وذلك باستخدام مجموعة عشوائية من التفاح من مربع كبير جدًا يحتوي على تفاح. في الصورة أدناه ، نرى التأثير الحقيقي لحجم العينة على القياسات: تأثير تفاحة واحدة مهم للغاية بالنسبة للعينات الصغيرة ويصبح أقل وأقل أهمية ، كلما زاد حجم العينة.
تعتمد مساهمة تفاحة واحدة على حجم العينة.فهم تأثير حجم العينة هو الأساس الأول لفهم اختبار الفرضيات. يمكننا أن نبدأ في القول بأن 0.5 على 2 تفاح سيكون مثل اختلاف تفاحة واحدة ، صغيرة جدًا. لكن بالنسبة لـ 100 تفاحة ، سيشكل 0.5 اختلافًا عن 50 تفاحة: فرق كبير جدًا!
بالنسبة للعينات الصغيرة ، يمثل 0.5 نقطة اختلافًا بسيطًا ، ولكن بالنسبة للعينات الكبيرة 0.5 ، هذا فرق كبير.كم يجب أن تكون العينة: اختبار الفرضية وأهميتها كإجابة
هناك عدة طرق للإجابة على هذا السؤال ، لكنني في هذه المقالة سأذهب إلى الاستدلال الإحصائي أو اختبار الفرضيات.
اختبار الفرضيات هو مجموعة من الأساليب الإحصائية المستخدمة لفهم كيف يمكن استخدام أخذ العينات من الأشياء الملاحظة لقبول أو رفض فرضية محددة مسبقًا. يستخدم اختبار الفرضيات لحل العديد من المشكلات ، لا سيما في البحث العلمي وكطريقة أساسية في التسويق عبر الإنترنت (اختبار A / B).
طور علماء الرياضيات اختبار الفرضيات بحيث يكون هناك إجراء معين للعثور على الحقيقة.
يتيح لك اختبار الفرضيات اختبار الفرضيات فقط ، ولكن ليس تطويرها.من المربع الذي يحتوي على 100 تفاحة (دعنا نسميها السكان) ، نأخذ عينة من 8 تفاح. هذا العام ، من بين 8 تفاح ، تم تعفن 5 (62٪) ، وفي العينة العام الماضي ، من 8 تفاح ، فقط 4 تعفن (50٪). نريد استخدام اختبار فرضية لتحديد ما إذا كانت نسبة التفاح الفاسد هذا العام أكبر من العام الماضي.
اختبار الفرضيات هو بديل رياضي لقياس السكان. بفضل هذه الحسابات ، يمكننا تعميم قياسات عينة صغيرة على عدد كبير من السكان. لذلك نحن نقوم بعمل أقل.
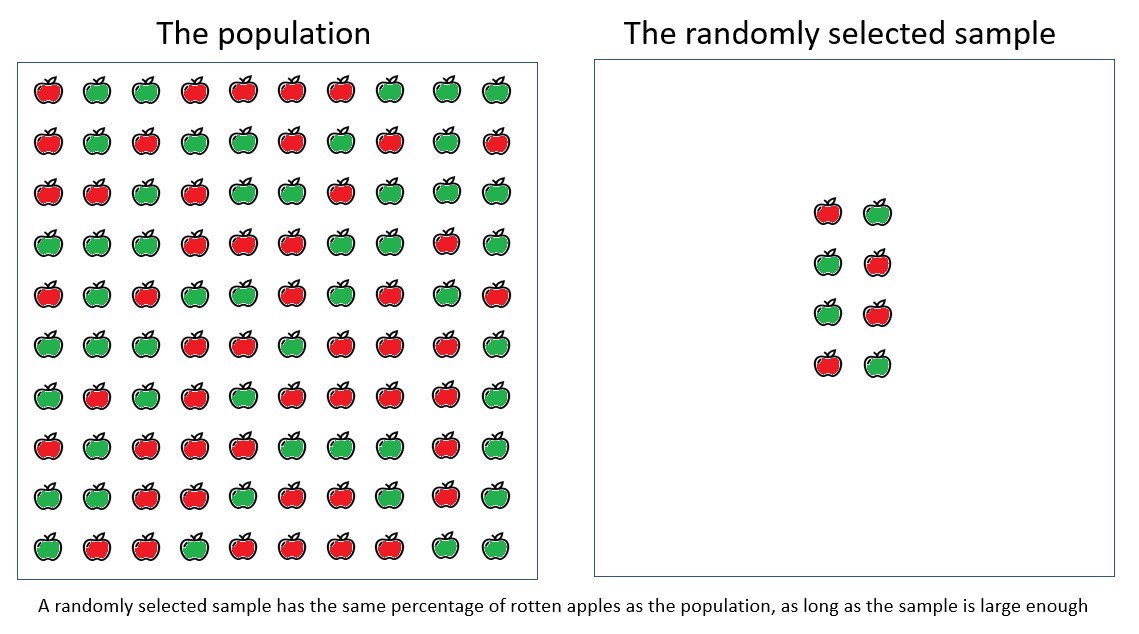
تحتوي العينة التي تم أخذ عينات منها عشوائياً على نفس النسبة المئوية من التفاح الفاسد مثل عامة السكان ، شريطة أن تكون العينة التي تم أخذ عينات منها كبيرة بدرجة كافية.
توصل علماء الرياضيات إلى طريقة لتعميم الاستنتاج بناءً على العينة لعامة السكان.
تبدأ هذه الطريقة في صياغة فرضية بحثية واضحة. لسوء الحظ ، لا تعمل الرياضيات إلا إذا كانت لدينا بالفعل فكرة عما نريد اختباره.
الفرضية الرئيسية لمثالنا:
كانت نسبة التفاح الفاسد في عموم السكان هذا العام أكثر مما كانت عليه في الماضي.اختبار الفرضية الفعلية
تشكل رياضيات اختبار الفرضية توازنًا بين نتيجة قياسات العينة وعدد المشاهدات. والنتيجة هي قيمة p.تمر هذه الحسابات من خلال استخدام التوزيعات: لكل حالة تخيلية تقريبًا ، تم استنباط قانون رياضي يصف النتيجة المتوقعة.
بالنسبة إلى نعم / لا أسئلة ، مثل مسألة تفاحنا الفاسد (الفاسد / غير الفاسد) ، ينطبق قانون رمي العملة المعدنية. هذا هو أبسط مثال للقانون الرياضي: 50 ٪ ذيول ، 50 ٪ النسر.
يمكن أيضًا تمثيله ببساطة كتوزيع رياضي قياسي يخبرنا باحتمالية الملاحظات. على سبيل المثال ، انخفض 7 نسور من أصل 10 تقلب العملة. يسمى هذا التوزيع ذو الحدين ويمكن تمثيله على النحو التالي:
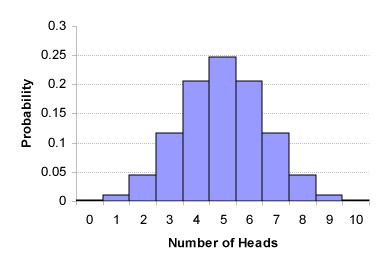توزيع ذات الحدين من 10 عملة تقلب.في هذه المقالة ، سأكون بعيدًا عن الرياضيات الصعبة ، لكن من المهم معرفة أنه يمكننا استخدام الصيغ الرياضية لتقييم ما إذا كانت النسبة المئوية المرصودة بعيدة عن النسبة المتوقعة.
في نهاية هذه المقالة سأقدم لك قائمة من صيغ اختبار الفرضيات الشائعة الاستخدام في الحالات المختلفة ، وبعد ذلك سأشرح كيفية استخدامها. لكن أولاً ، سأشرح تفسير اختبار الفرضيات.
نتيجة اختبار الفرضية: قيمة p
وراء اختبار الفرضية ، يوجد توازن رياضي بين القيم المرصودة وحجم العينة. في نهاية العمليات الحسابية ، سينتج عن كل خيار اختبار فرضية موجود درجة قياسية تسمح لك بمقارنة النتيجة حتى عندما لا تكون الرياضيات هي نفسها.
P-value هي طريقة قياسية لصياغة نتيجة اختبار الفرضيات واستخدامها في أي اختبارات أخرى.
قيمة P هي رقم بين 0 و 1 يخبرنا إذا كان الفرق بين ملاحظاتنا للعينات وافتراضاتنا مختلفة تمامًا. القيمة المرجعية هي 0.05.
الفرق مهم من الناحية الإحصائية إذا كانت قيمة p أقل من 0.05.
والفرق ليس ذو دلالة إحصائية إذا كانت قيمة p أكبر من 0.05.
مثال 1:
حققنا 10 تقلب عملة.
فرضيتنا: نتوقع 5 ذيول.
ملاحظاتنا: حصلنا على 6 ذيول.
حقق حساب القيمة p 0.518 ، وهو أكثر من 0.05.
استنتاجنا: الفرق ليس ذو دلالة إحصائية.
تفسيرنا: النتيجة متوافقة مع الفرضية.
مثال 2:
حققنا 10 تقلب عملة
فرضيتنا: نتوقع 5 ذيول.
نتيجة لدينا: حصلنا على 10 ذيول.
قيمة p هي 0.0 ، أي أقل من 0.05.
استنتاجنا: الفرق مهم من الناحية الإحصائية
تفسيرنا: النتيجة ليست متسقة مع الفرضية.
مثال 3:
فحصنا 10 تفاح.
فرضيتنا: نتوقع تفاحة واحدة فاسدة.
نتائجنا: حصلنا على 1 تفاحة فاسدة.
قيمة p هي 1.0 والتي تزيد عن 0.05.
استنتاجنا: الفرق ليس ذو دلالة إحصائية
تفسيرنا: النتيجة متوافقة مع الفرضية.
مثال 4:
فحصنا 10 تفاح.
فرضيتنا: نتوقع تفاحة واحدة فاسدة.
نتيجة لدينا: حصلنا على 5 تفاح فاسد.
لدينا قيمة ف هي 0.0114 وهو أقل من 0.05.
استنتاجنا: الفرق مهم من الناحية الإحصائية
تفسيرنا: النتيجة ليست متسقة مع الفرضية.
استنتاج
في هذه المقالة ، أعطيت تفسيرًا بديهيًا للهيكل العام للأخطاء الإحصائية أو اختبار الفرضيات. آمل أن تفهم الآن اختبار الفرضيات بشكل أفضل ، وكيف يمكن أن يكون مفيدًا لك.
لم أتعمق في البراهين الرياضية وتفاصيل محددة. يقدم الجدول أدناه قائمة بأكثر اختبارات الفرضيات شيوعًا والتي أوصي بها لمزيد من الدراسة.
قائمة بفرضيات بديلة لبعض اختبارات الفرضيات.
آمل أن تكون هذه المقالة مفيدة لك ، وأتمنى لك التوفيق في إجراء مزيد من البحوث حول اختبار الفرضيات.